非线性弦振动方程的最优系统、不变解及守恒律

张 寒

(聊城大学 数学科学学院，山东 聊城 252059)

0 引言

偏微分方程是现代数学的一个重要分支，常被用来描述力学、物理等领域的问题，对这些领域的发展起着重要的推动作用。研究人员提出了许多求解偏微分方程的方法,其中包括齐次平衡法[1-2]、经典李群法[3-5]、CK直接约化法[6-7]等。

本文将研究非线性弦振动方程

utt-(arctanu)xx=0，

(1)

其中u是关于x,t的未知函数。文献[8]利用变分原理得到了非线性弦振动方程，赋予该方程深刻的物理意义，并用减缩摄动法将非线性弦振动方程变换为易于求解的普通KdV方程。文献[9]通过使用双曲函数法，得到了非线性弦振动方程的一类扭状精确孤立波解,并进一步推广了双曲函数法的思想，从而获得了更多的精确解。文献[10]利用试验函数法得到了非线性弦振动方程的孤波解和周期波解。Bluman等[11-12]介绍了李对称在偏微分方程中的应用。Ovsiannikov[13]提出了一种利用伴随变换的全局矩阵来构造最优系统的直接算法。

在上述文献的基础上，拟完成如下工作：一是求解出非线性弦振动方程的对称，二是推导出非线性弦振动方程的一维子代数的最优系统，三是通过约化方程得到精确解包括幂级数解，四是分析该方程的守恒律。

1 非线性弦振动方程的对称

考虑一个单参数李群的无穷小变换：

x*=x+εξ(x,t,u)+o(ε2),t*=t+ετ(x,t,u)+o(ε2)，u*=u+εφ(x,t,u)+o(ε2)，

其中ξ(x,t),τ(x,t),φ(x,t)是关于x,t,u的未知函数，ε是无穷小参数。由上述方程可知，方程(1)的向量场可以表示为

(2)

根据李群理论，得到二阶延拓

其中

φx=Dx(φ-ξux-τut)+ξuxx+τutx,

φxx=Dxx(φ-ξux-τut)+ξuxxx+τutxx，

φtt=Dtt(φ-ξux-τut)+ξuxtt+τuttt。

从不变性的条件来看，有

Pr(2)V(Δ)|Δ=0=0，

(3)

其中Δ=utt-(arctanu)xx。通过求解方程(3)，可以得到方程(1)的超定方程组,它们分别是

ξx=τt,ξt=ξxx=0,ξu=0,τu=τx=0,φ=0,

求解上述方程组，可以推出

ξ=c1x+c2,τ=c1t+c3,φ=0,

其中c1,c2,c3是任意的常数。由上述结果得到方程(1)的不变群生成元为

V=(c1x+c2)∂x+(c1t+c3)∂t。

(4)

由方程(4)可得

V1=t∂t+x∂x,V2=∂x,V3=∂t。

为了得到对称群，求解带有初始问题的常微分方程

利用Vi(i=1,2,3)得到方程(1)的单参数变换群Gi(i=1,2,3)：

(5)

由式(5)中的单参数群Gi(i=1,2,3)可以得到方程(1)的解的表达式为

G1*u(x,t)=u1(e-εx,e-εt),G2*u(x,t)=u2(x-ε,t),G3*u(x,t)=u3(x,t-ε)。

由李括号和伴随变化的定义可知

[Vi,Vj]=ViVj-VjVi,

可以分别得到表1和表2。

表1 换位子表

表2伴随变换

AdV1V2V3V1V1eεV2eεV3V2V1-εV2V2V3V3V1-εV3V2V3

2 一维子代数的最优系统

对称子代数的一维最优系统在寻找偏微分方程的不变解方面起着不可或缺的作用。为了得到更丰富的解，需要对伴随变换矩阵进行分析。接下来，将构造方程(1)的一维子代数的最优系统。

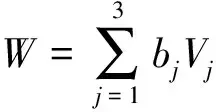
(a1V1+a2V2+a3V3)-ε[b1V1+b2V2+b3V3,a1V1+a2V2+a3V3]+o(ε2)=

(a1V1+a2V2+a3V3)-ε(N1+N2+N3)+o(ε2),

(6)

其中Ni=Ni(a1,a2,a3,b1,b2,b3)(i=1,2,3)可以从表1中得到。如果对任意的bj(j=1,2,3)，有公式

(7)

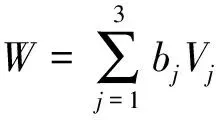
N1=0，N2=b2a1-b1a2，N3=b3a1-b1a3。

然后把N1,N2,N3代入方程(7),提取bj的系数，有

(8)

求解方程组(8)，发现η(a1,a2,a3)=R(a1)，这说明方程(1)仅有一个不变量a1。

接下来，就是求解方程(1)的伴随变换矩阵A,

A=A1A2A3,

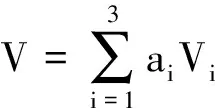
Ad(exp(ε1V1))V=a1Ad(exp(ε1V1))V1+a2Ad(exp(ε1V1))V2+a3Ad(exp(ε1V1))V3=

a1V1+eε1a2V2+eε1a3V3=(a1,a2,a3)A1(V1,V2,V3)T,

其中

用同样的方法，依次求得

所以方程(1)的伴随变换矩阵为

将一般伴随变换Ad(exp(ε3V3))Ad(exp(ε2V2))Ad(exp(ε1V1))作用在V上，V有以下变换：

V=(a1,a2,a3)→(d1,d2,d3)=(a1,a2,a3)A。

(9)

最后，要考虑不变量的阶数，若不变量的阶数是偶数，考虑η=0,η=1,η=-1这三种情况，如果不变量的阶数是奇数，考虑η=0,η=1这两种情况。

情形1a1=1。

取一个代表元V*=V1,将d1=1,d2=d3=0代入方程(9)中，得到ε2=a2eε1,ε3=a3eε1,其中ε1是任意常数。以上结果说明方程(1)的任意一维子空间与V1等价。

情形2a1=0。

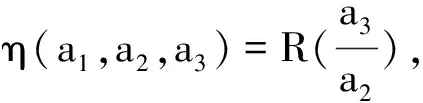
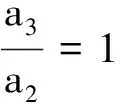
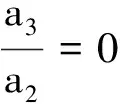
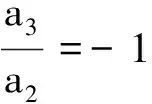
综上所述，方程(1)的最优系统为V1,V3,V2+V3,V2-V3。

3 不变解

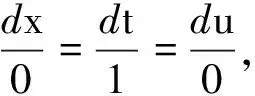
u=f(x)。

(10)

把方程(10)代入到方程(1)中，得到相似约化方程(arctanf)zz=0，求解上式方程，得u=tan(c1x+c2),c1,c2是任意的常数。

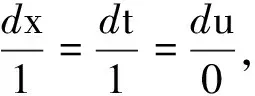
u=f(x-t)。

(11)

把方程(11)代入方程(1)，得到相似约化方程

2ffz2+(f4+f2)fzz=0。

(12)

假设方程(12)有

(13)

形式的解，把方程(13)的幂级数展开代入方程(12)，有

一般的，当n≥0时

当n=0时，有

即当d0≠0,d1为任意的常数时，dn+2已经被确立。所以方程(1)的解可以表示为

4 守恒律

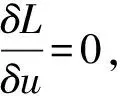
(14)

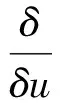
根据Ibragimov的结论,方程(1)的守恒律由式Dx(Cx)+Dt(Ct)=0决定，向量场C=(Cx,Ct)由式

决定，其中W=φ-ζjuj。

下面讨论部分情况。

情形1 取λ(x,t)=xt，V2=∂x,则

Cx=xt(1+u2)2utt-4uxtux2+t(1+u2)ux,

Ct=ux(x+2u2+u4+4uxtut+4u3xtux)2utt-uxuxt(1+u2)2。

情形2 取λ(x,t)=x，V3=∂t,则

Cx=-ut(6uxux+1+u2)+x(1+u2)uxt,

Ct=x(-uuxx-u2uxx+2uux2)-xut(4uut+4u3ut)。

5 结论

本文分析了非线性弦振动方程的李对称，并利用直接算法计算出该方程一维子代数的最优系统。利用约化方程和幂级数展开法得到了该方程的精确解。最后，给出了非线性弦振动方程的守恒律。