一类带记忆项的热方程的爆破解
2022-05-07岳丽霞
杨 梓,岳丽霞
(兰州交通大学 数理学院,甘肃 兰州730070)
0 引言
含有记忆项的方程被应用于各个科学领域。例如:在核反应堆动力学研究中出现了涉及记忆项的模型[1-2],人口和人口动态[3],特别是涉及非延迟和遗传效应的逻辑增长模型[4-5]。随后,学者们研究了此类模型的各种广义解的有限时间可解性、稳定性和爆破性[6]。特别地,讨论了一类含有记忆项的半线性抛物型方程的爆破性质,这些记忆项产生于非牛顿流体中的黏弹性力模型中。
文献[7]提出了
(1)
并得到解将在有限时间内爆破,且爆破发生在边界。文献[8]在此基础上把边界条件从0到t积分得到了模型
(2)
得到了相似的结论。文献[9]对反应项进行关于时间的积分,得到如下的方程
(3)
其主要结论为当p+q>1时,u将在有限时间内爆破。
数十年来,尽管在包含反应记忆、扩散或两者的模型已经有了大量的突破,但在扩散模型的文献中,反应项和边界条件同时含有记忆项的模型结果并不常见。因此,本文在文献[7-9]的基础上研究了一类带记忆项的热方程
(4)
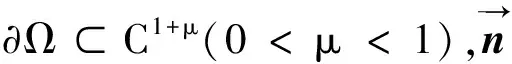
1 经典解
定理1 设GN(x,y,t,τ)是带有齐次Neumann边界条件的方程的格林函数,当t较小时,则
在问题(4)的条件下是一个压缩映射。
证明令
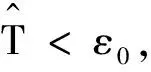
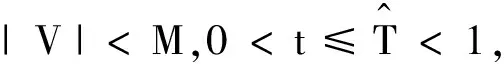
因此,Γ是X到X的一个自身映射,其中
对任意的v1,v2∈X,有
‖Γ[v1]-Γ[v2]‖∞≤
成立。取
则存在0<β<1,有
‖Γ[v1]-Γ[v2]‖∞≤β‖v1-v2‖∞
(5)
2 解的爆破
定理2 当p>1时,问题(4)的所有非平凡解都将在有限时间内爆破。
证明下文中cn或Cn(n=0,1,2,…)均代表不同的正常数。首先令格林函数GN满足
故由(5)式和Jensen不等式得
(6)
其中,令
由(6)式可得
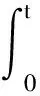
将上述不等式从0到t积分,可得
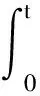
采用反证法,假设其有全局解v,那么对于任意T>0,都有
以≥10μmol/L为判定标准1473人中,HHT患者1223人,占全部高血压患者的83.02%;男性HHT患者564人,占男性高血压患者的90.67%,女性HHT患者659人,占女性高血压患者的77.49%。以≥15μmol为判定标准1473人中,HHT患者889人,占全部高血压患者的60.35%;男性HHT患者468人,占75.24%,女性HHT患者421人,占49.47%。以≥10μmol为标准无论总体、男性和女性组的HHT患病率比以≥15μmol为标准均升高了20%以上,均显示男性高于女性,且随年龄增加,HHT患病增高。
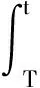
令
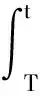
所以,对任意的T≤t≤2T,都有G(t)≥S(t)成立。其中,S(t)满足
(7)
在(7)式中第一个方程两端同时乘S′(T),并在(T,t)上积分,可得
对上式的两端同时从T到2T积分,可得
故可得
这与T足够大相违背,故问题(4)将在有限时间内爆破。
3 边界爆破
引理1 令v(x,t)是问题
(8)
的解,则v(x,t)关于时间t是不减的。 其中p>1,且c是一个正常数。
证明该证明与文献[12]的引理2.1的证明相似。即通过比较原则可知,问题(8)的解v(x,t)≥c,令
u(x,t)=v(x,t+k),
故u(x,t)满足:
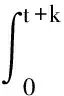
故得
u(x,t)≥v(x,t),
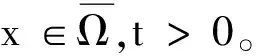

成立。
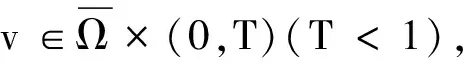
则对任意Ω′⊂Ω中,都有
sup{v(x,t),(x,t)∈Ω′×(0,T)}<∞
成立,此引理称为解的最值性质。
证明已在文献[13]的引理5.1做出证明,故此处不再做证明。
定理3 问题(4)的解在有限时刻的爆破只可能发生在边界上。
证明令
设
则由问题(4)的经典解和Jensen不等式有
故由上式得
由Jensen不等式可得
上式的左右两端同乘F′(t),并在区间(0,t)上积分可得
将上式在区间(t,T)上积分,可得
由
等价于
(9)
取任意Ω′⊂Ω,使d(∂Ω,Ω′)=ε>0,对于取定的Ω′,再取Ω″⊂Ω,使得Ω′⊂Ω″,并有
故对于∀ε>0,有
成立。由问题的经典解、引理1以及(9)式可得
由引理2可知
(10)
其中φ(x)满足
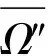
4 结论
本文研究了一类具有记忆项热方程的爆破问题。首先利用Banach压缩映射定理建立了问题的经典解,后在此基础上证明了当p>1时,该方程的所有非平凡解将在有限时间内爆破,并证明了解的爆破仅会在边界上发生。
