基于MATLAB的电力系统暂态稳定仿真与分析
2022-05-07何芳
何 芳
(滨州学院 电气工程学院,山东 滨州 256603)
电力系统暂态稳定是指电力系统在某个运行方式下突然受到大的干扰后,经过暂态过程达到新的稳态运行方式或恢复到原来的运行状态。随着电力系统规模的持续扩大,电网内部联系越来越复杂,电力系统发生短路故障往往会引起“连锁反应”,即电网中某处发生故障,可能引起同步发电机的功角振荡,破坏整个电力系统的稳定性,从而造成大量发电机切机、用户停电的事故,甚至导致整个电力系统的崩溃,后果极其严重。因此研究电力系统暂态稳定与控制方法对电力系统的安全稳定运行具有重要的意义。
电力系统暂态稳定的分析方法主要有能量函数法、时域仿真法等[1-3]。能量函数法主要基于Lyapunov稳定性定理和Lasalle不变原理[4],通过对构造的能量函数的分析,给出系统的稳定性分析结果。主要包括:主导不稳定平衡点的能量函数法、势能边界曲面法、BCU法、扩展等面积法则[5]等。但能量函数构造困难、形式复杂,并且模型的适应性差。
时域仿真法是通过求解描述故障发生前、故障期间和故障切除后电力系统运行状态的微分-代数方程组得到各发电机转子摇摆曲线,根据各发电机是否能够同步运行来判断系统的暂态稳定性。时域仿真法通过对足够精确的数学模型进行分析,得到较为准确的计算结果,可以作为其他分析方法准确性的评判标准或提供可靠的分析数据,目前已有相当成熟的商业软件,如MATLAB、PSS/E、PSASP、BPA等。时域仿真法在线应用时计算量大,对硬件设备要求高[6]。本文采用时域仿真法分析自动重合闸对电力系统暂态稳定的影响。
1 自动重合闸对暂态稳定的影响
瞬时性故障指持续时间很短且引起故障的因素能短时间内自行消失的故障类型。电力系统的短路故障80%以上是瞬时性故障,采用自动重合闸一次成功的概率很高[7],不但增加了供电的可靠性,缩小了停电范围,而且增大了系统的减速面积,有利于提高系统的稳定性。暂态稳定极限切除角是一个判断系统稳定程度的重要指标,暂态稳定极限切除角越大系统稳定性越好。
1.1 自动重合闸对发生瞬时性故障系统暂态稳定的影响
未装设自动重合闸时,根据等面积定则,极限切除情况下有

(1)
此时极限切除角为
(2)
装设自动重合闸装置后,设自动重合闸合闸时,发电机的功角为δg,

(3)
可推得极限切除角为
(4)
由式(1)~(4)可知,相同运行状况的电力系统,自动重合闸合闸成功能提高系统的极限切除角,进而提高系统的暂态稳定性。
1.2 自动重合闸对发生永久性故障系统暂态稳定的影响
永久性故障指故障因素不能自行消失,不采取措施不能恢复正常供电的故障类型。永久性故障时,自动重合闸启动闭合故障线路的断路器,相当于又一次发生了接地故障,此时非但没有增大减速面积,反而会减小减速面积,对系统的稳定性造成二次冲击,从而降低系统的暂态稳定性。因此,考虑到电力系统暂态稳定,在自动重合闸动作前需要先判断出短路故障是瞬时性还是永久性故障[8]。随着自适应自动重合闸技术的发展,虽然自适应单相自动重合闸的研究已经取得了一定成绩,但三相自动重合闸目前尚无可靠方便的方法判别瞬时性故障与永久性故障,但如果选择合适的自动重合闸时间,可以有效地避免第二次故障冲击加剧电力系统的摇摆。
1.3 永久性故障时三相自动重合闸合闸时间的选取
最佳重合闸时间条件:功角达到最大值并开始减小,角速度为负并在达到负最大值之前,对于最佳重合时间的选取[9-12],以单机无穷大系统为例来说明,发电机采用二阶模型,其转子的摇摆方程为
采用MATLAB里求解常微分方程的龙格-库塔法,可以直接绘制出发电机在故障时和故障后的δ-t曲线。龙格-库塔法解发电机转子摇摆方程的流程:(1)根据运行条件计算所需的初始值Ei、δi;(2)形成电力网络的回路阻抗矩阵;(3)若发生故障则根据故障情况修改回路阻抗矩阵,求得系统的转移阻抗;(4)在指定的时间区间内求解转子摇摆方程,得到发电机转子δ-t曲线。
根据故障后的δ-t曲线可得,当短路故障被切除后,系统输出的电磁功率大于输入的机械功率,系统开始减速,积累减速能量,此时自动重合闸动作,在永久性故障持续时闭合断路器,等效于系统又发生短路故障,系统输出的电磁功率小于输入的机械功率,系统又会积累加速能量。如果自动重合闸合闸太早,造成加速能量积累的太少,而加速能量会大于减速能量,造成系统的二次振荡失稳。故最佳重合闸时间为当系统的功角达到最大并开始减小,角速度为负并逐渐增大到最大值之前。
2 单机无穷大系统的仿真分析
在MATLAB/Simulink上搭建单机无穷大系统(图1)。
2.1 自动重合闸合闸成功对系统暂态稳定的影响

图1 单机无穷大系统接线图
当发生AB两相接地短路故障时,假设0.25 s保护动作切除故障。未安装自动重合闸装置时,系统功角持续增大,系统失稳,如图2(a)所示。当安装自动重合闸装置且在0.4 s合闸成功时,系统功角趋近于一个稳定值,系统具有暂态稳定性,如图2(b)所示。由此可见,自动重合闸于瞬时性故障时,有利于提高系统的暂态稳定性。
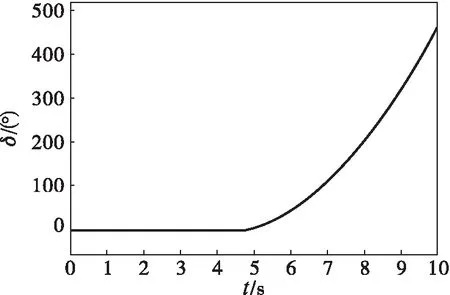
(a)无自动重合闸
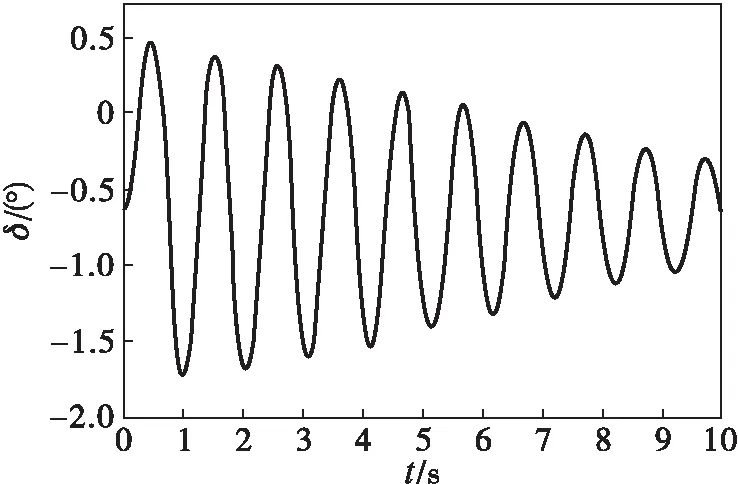
(b)自动重合闸合闸成功
2.2 瞬时性故障时自动重合闸合闸时间对暂态稳定极限切除角的影响
由式(2)得,未安装自动重合闸装置时,系统极限切除角为63.61°,根据发电机转子故障后的δ-t曲线,可得其极限切除时间为0.217 s,图3(a)显示系统功角变化已经接近等幅振荡,说明系统已达到暂态稳定的极限。当系统安装了三相一次自动重合闸装置,且在发生瞬时性故障0.400 s合闸成功时,根据发电机转子故障后的δ-t曲线和式(4)得,极限切除角为79.1°,极限切除时间为0.298 s,图3(b)显示系统功角变化已经接近等幅振荡,说明系统已经达到暂态稳定的极限,其极限切除时间提高了0.071 s。
2.3 合闸方式对系统暂态稳定的影响
图3(c)为系统发生了AB两相接地短路故障时,采用自动重合闸AB两相的方式,并在0.400 s时合闸成功,其极限切除时间为0.315 s,与图3(b)相比,其极限切除时间提高了0.017 s,表明采用重合短路故障相的方式有利于提高系统的暂态稳定性。
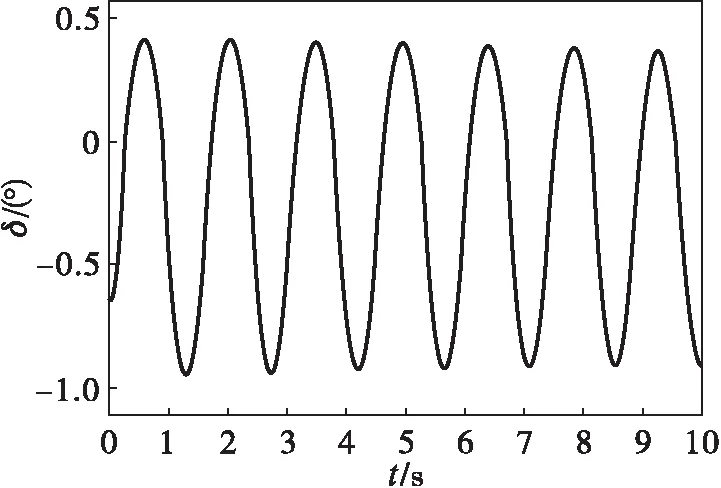
(a) t=0.217 s
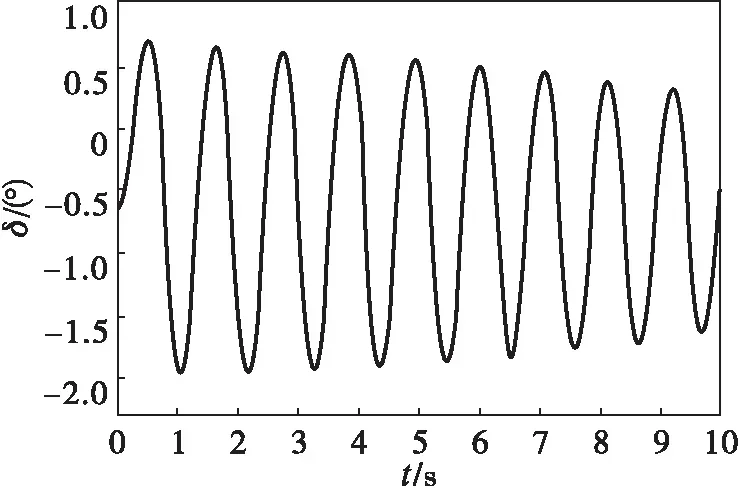
(b) t=0.298 s
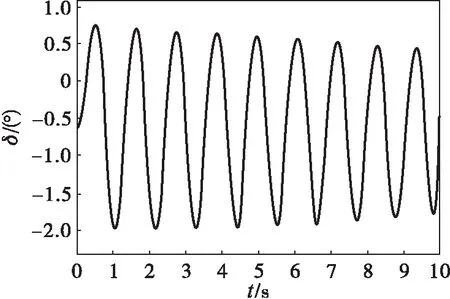
(c) t=0.315 s
2.4 永久性故障时重合闸时间仿真分析
根据发电机转子故障后的δ-t曲线可得,系统在0.430 s时功角达到最大值并开始减少,而转速开始变为负的最大值时刻为0.630 s,故最早自动重合闸合闸时间为0.630 s。图4(a)显示,系统发生AB两相接地故障,继电保护装置在0.190 s断开断路器,隔离故障,自动重合闸在0.423 s时合闸,后在0.533 s重新断开断路器,仿真结果表明此时系统失稳。由图4(b)可知,自动重合闸在0.630 s时合闸,后在0.730 s重新断开断路器,仿真结果表明此时系统接近等幅振荡,系统处于临界稳定状态。
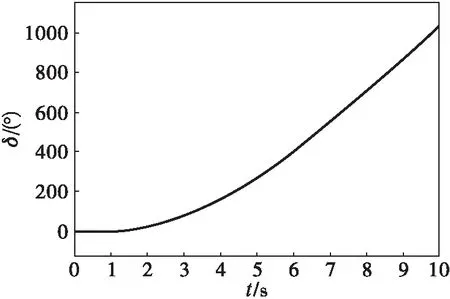
(a) t=0.423 s
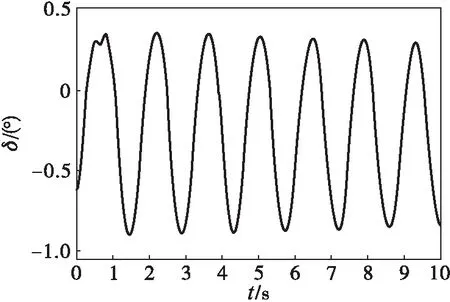
(b) t=0.630 s
3 多机复杂电力系统的仿真分析
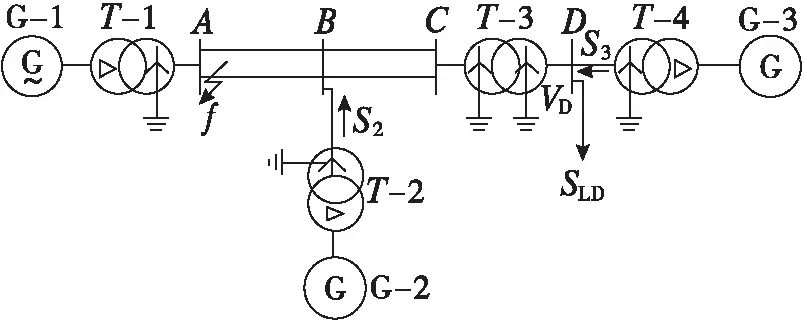
图5 某三机系统接线图
多机电力系统采用某三机系统[13]如图5所示。
多机电力系统输出的功率是所有发电机功角函数:
(5)
多机复杂电力系统的暂态稳定是通过机组之间的相对功角随时间变化的情况来判定,只要有一个相对功角随时间不断增大或减小,系统就判定为不稳定[12-14]。
3.1 多机电力系统暂态稳定的判定
多机电力系统暂态稳定的判定流程:(1)根据接线图和参数建立系统的接电阻抗矩阵Z,并求出阻抗角的余角矩阵α;(2)将电阻抗矩阵和余角矩代入式(5)建立故障前和故障后系统的数学模型;(3)编制程序求解发电机转子摇摆曲线;(4)判定系统的暂态稳定。
3.2 仿真分析
图6(a)显示,当系统发生三相短路故障且故障持续时间为2.2 s,故障线路没有安装自动重合闸装置时,G-2与G-3之间的功角差及G-1与G-3之间的功角差随着时间逐渐增大,系统失去暂态稳定性。图6(b)显示故障线路安装自动重合闸并在故障后2.1 s重合成功时,三台发电机两两之间的功角差都随时间逐渐趋近稳定,系统具有暂态稳定性。因此自动重合闸能有效地提高多机系统的暂态稳定性。
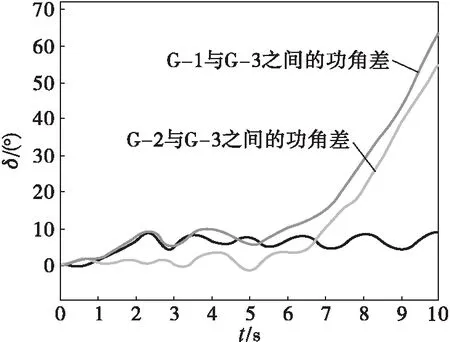
(a) 无自动重合闸
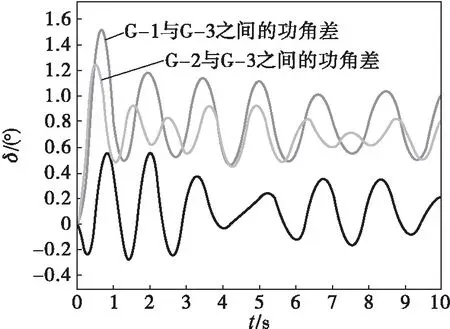
(b) 有自动重合闸
4 结论
本文分析了瞬时性故障及永久性故障时,自动重合闸对暂态稳定的影响,以及永久性故障的三相自动重合闸合闸时间的选取方法。利用通过Simulink搭建了单机无穷大系统和某三机系统模型,进行了暂态稳定的仿真,结果表明:自动重合闸能有效提高系统的暂态稳定性。电力系统暂态稳定的自动重合闸最佳重合闸时间的分析为重合闸时间设计和整定提供了参考价值。
