具有恐惧效应和半封闭捕获的Holling-Ⅱ类时滞捕食系统Hopf分岔

刘 娟，张子振

(1.蚌埠学院 理学院；2.安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030)

近年来，国内外研究学者从不同的角度研究了生物系统的动力学。捕食者-食饵之间的相互作用是生物系统和种群动力学中的一个重要的研究领域。文献[1-3]研究了基本的两种群捕食系统。考虑到种群之间的相互作用的复杂性，文献[4-7]则研究了三种群捕食系统。由于每个种群具有不同的成长阶段，文献[8-10]研究了具有阶段结构的捕食系统。最近，魏臻[11]考虑到食饵种群因对捕食者的恐惧而影响其繁殖能力，以及为了保证种群的合理开发利用，提出了如下具有恐惧效应和半封闭捕获的Holling-Ⅱ类捕食系统，并研究了系统的局部和全局稳定性，

(1)

在现实世界中，捕食者种群吃掉食饵种群以后，需要经过一定的妊娠周期才可以不断繁殖后代。即，系统(1)忽略了捕食者种群的妊娠时滞。另外，时滞对于种群动力系统具有非常重要的影响，它可以影响系统的稳定性，导致系统从稳定变得不稳定，从而使得系统中的种群产生周期震荡。因此，本文在系统(1)中引入捕食者种群的妊娠时滞，研究具有恐惧效应和半封闭捕获的Holling-Ⅱ类时滞捕食系统

(2)

其中，τ表示捕食者种群的妊娠时滞。

1 Hopf分岔的存在性

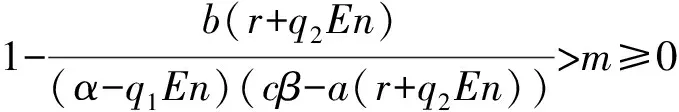
系统(2)在E*(x*，y*)处的特征方程为

λ2+J1λ+J0+(K1λ+K0)e-λτ。

(3)

其中，

J0=j11j22，J1=-(j11+j22)，K0=j11k22-j12k21，K1=-k22，

当τ=0时，方程(3)变为

λ2+(J1+K1)λ+J0+K0=0。

(4)

引理1[11]当条件(T1)成立，或者条件(T2)成立且K>M时，方程(4)的特征根均具有负实部。即，当τ=0时模型(2)是局部渐近稳定的。其中，

当τ>0，假设λ=iω(ω>0)为方程(3)的根，则可以得到

(5)

方程(5)左右两边平方相加，有

(6)

令ω2=σ，则方程(6)变为

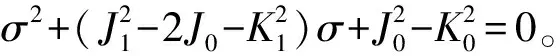
(7)

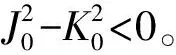
定理1 对于系统(2)，如果条件(T1)成立，或者条件(T2)成立且K>M时，当τ∈[0,τ0)时，系统(2)局部渐近稳定；当τ=τ0时，系统(2)在E*(x*,y*)处产生Hopf分岔。

2 仿真示例

选取α=0.8，K=2，b=0.01，β=0.5，a=0.5，m=0.8，q1=2.5，E=1，n=0.1，r=0.2，c=0.8，q2=1。得到系统(2)的示例模型

(8)

利用MATLAB软件计算得到示例模型(8)存在唯一正平衡点E*(6.0000,0.6424)。由此可以得到ω0=1.0227，τ0=1.0196。通过计算可以验证，示例模型(8)产生Hopf分岔的条件成立。当τ=0时，示例模型(8)局部渐近稳定，其状态轨迹和相图如图1所示。接下来，选取τ=0.5068∈(0,τ0)，此时的状态轨迹和相图如图2所示。仿真效果显示示例模型(8)局部渐近稳定。

图1 当τ=0时，示例模型(8)的状态轨迹和相图

图2 当τ=0.5068时，示例模型(8)的状态轨迹和相图

当选取τ=1.9598>τ0，示例模型(8)失去稳定性，在E*(6.0000,0.6424)处产生Hopf分岔，其状态轨迹和相图如图3所示。

此外，选取n=(0.10,0.15,0.20)，其他参数值固定不变。由图4所示的相图可以看出，随着食饵种群和捕食者种群可供捕捞的比例减小，示例模型(8)将由稳定状态进入混沌状态。因此可以看出，示例模型(8)存在过剩捕捞现象，不利于区域内食饵种群和捕食者种群的生态平衡。

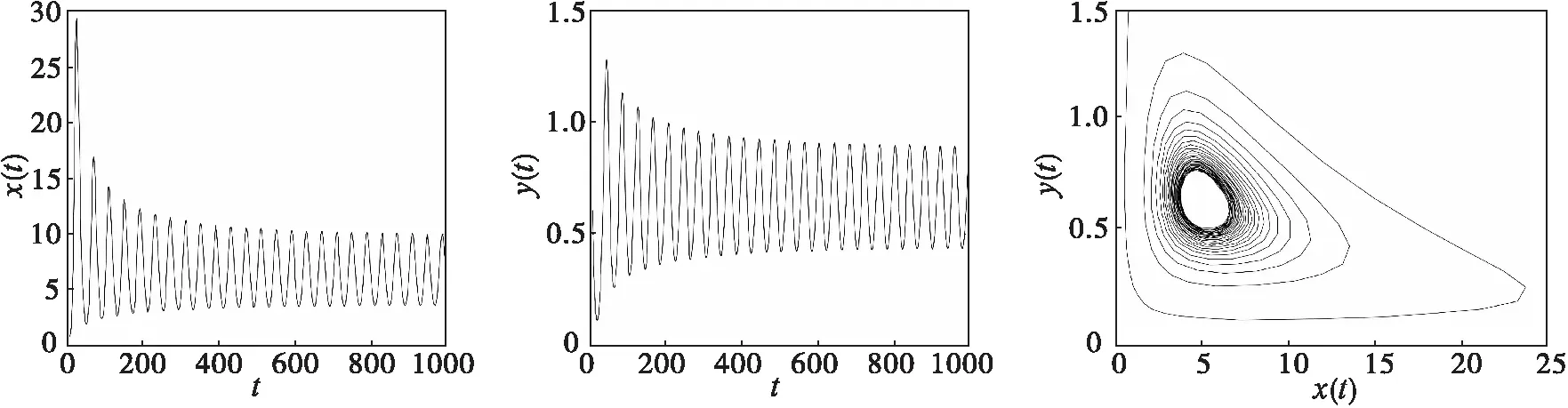
图3 当τ=1.9598时，示例模型(8)的状态轨迹和相图

3 小结

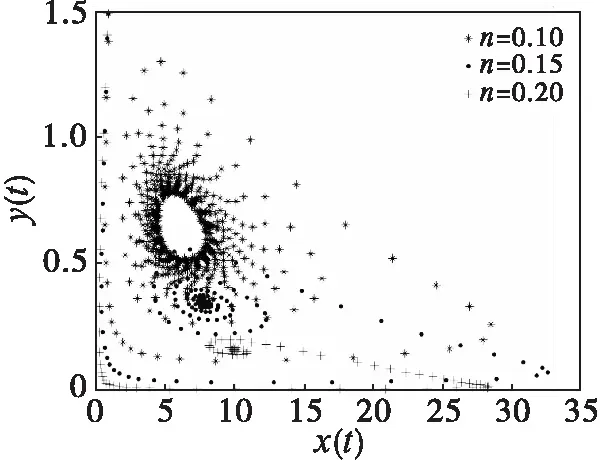
图4 混沌状态的相图

本文在文献[11]的基础上，进一步引入了捕食者种群的妊娠时滞，研究了一类具有恐惧效应和半封闭捕获的Holling-Ⅱ类时滞捕食系统。首先给出系统存在唯一正平衡点的充分条件并计算出正平衡点的表达式。然后以捕食者种群的妊娠时滞为分岔，讨论了系统局部渐近稳定和产生Hopf分岔的存在性。研究表明，在一定条件下，系统是局部渐近稳定的，食饵种群和捕食者种群处于理想的稳定状态。但是，当时滞的取值越过产生Hopf分岔的临界点时，食饵种群和捕食者种群处于周期震荡状态。另外，仿真效果表明，对于食饵种群和捕食者种群过剩捕捞，不利于区域内食饵种群和捕食者种群的生态平衡。