薄壁圆钢管约束陶粒混凝土短柱轴压性能研究

郑宏宇，郑峻，柯晓军，朱振，孟淼，郑煜缤

( 1.广西大学 土木建筑工程学院 ， 广西 南宁 530004；2.工程防灾与结构安全教育部重点实验室， 广西 南宁 530004；3. 广西建工集团第五建筑工程有限责任公司设计研究院， 广西 南宁 530001)

0 引言

钢管混凝土柱不但承载力高，而且延性好、抗震性能优良，因此，在高层、超高层建筑结构和桥梁结构中已得到了广泛应用，设计计算理论也较为成熟[1-3]。我国现行的钢管混凝土规范[4]和规程[5]为避免钢管局部屈曲对构件受力性能的不利影响，分别规定钢管外径不宜小于168、200 mm，壁厚不宜小于3、4 mm，径厚比不宜超过135×(235/fy)(fy为屈服强度)，套箍系数宜在0.5～2.0，但国内外学者的研究表明，在上述限值之外的薄壁钢管约束普通混凝土或常规钢管填充轻骨料混凝土的柱子也具有良好的受力性能[6-12]，并且发现，薄壁钢管填充轻骨料混凝土的短柱轴压性能更优[7]。薄壁圆钢管的径厚比D/t大于空钢管局部稳定限值的1.5倍或壁厚小于3mm[13]，薄壁圆钢管混凝土柱破坏前钢管一般不发生局部屈曲[6，7]，且常规钢管对轻骨料混凝土的约束作用弱于普通混凝土[8-9]，薄壁圆钢管混凝土短柱(指长径比L/D≤4的柱)在轴压作用下不发生局部失稳的径厚比限值为331×(235/fy)[10]，常规钢管混凝土在多、低层建筑中的经济性不佳[11]。由于轻骨料混凝土的弹性模量较低，因此采用薄壁钢管进行约束，在力学性能上更为匹配，既克服了薄壁钢管易发生局部屈曲和轻骨料混凝土弹性模量较低、脆性大的缺点，还可更大限度地减轻结构自重，减小地震效应，减少用钢量，降低造价[11]，在大跨桁架、网架[12]、既有建筑增层改造的新增楼层柱、电杆、输电塔、支架、栈桥等结构中具有较为广阔的应用前景。当采用工业废料制成的轻骨料时，还具有明显的环保意义。

目前，关于薄壁钢管约束轻骨料混凝土柱受力性能和计算方法的研究相对有限[14-17]，规范、标准和规程也未涵盖这类构件。为此，本文设计、制作4个径厚比为(80.5、125.0)(76.8、122.8)×235/fy、套箍系数小于0.5的薄壁钢管陶粒混凝土短柱试件，以薄壁钢管壁厚、核心陶粒混凝土强度为变化参数，通过轴心受压静力加载试验，观测受力全过程和破坏特征，采集轴压变形量、钢管应变、特征荷载，研究其轴心受压承载力和延性，分析套箍系数对极限承载力、核心陶粒混凝土抗压强度提高系数、柱子延性的影响规律，以期为薄壁钢管陶粒混凝土柱的应用提供试验依据。

1 试验概况

1.1 材料力学性能参数测试

钢管均为Q235直缝焊接钢管，从钢管上截取标准钢材试件，在其正反面粘贴纵、横向应变片，测得的钢管材料力学性能指标见表1。采用页岩粉煤灰陶粒作为粗骨料，粒径不大于10 mm×20 mm，堆积密度为726.5 kg/m3，筒压强度为6.12 MPa，24 h吸水率为7.2%。水泥采用P.O 42.5级普通硅酸盐水泥；细骨料采用细度模数为2.6的普通中砂。按《轻骨料混凝土结构技术规程 》(JGJ 12—2006)规定的强度等级CL20和CL30配制2种陶粒混凝土，具体配合比见表2，测得2种陶粒混凝土的力学性能指标见表3。

表1 钢管材料力学性能指标Tab.1 Mechanical properties of steel tube

表2 陶粒混凝土的配合比Tab.2 Mix ratio ofceramsite concrete

表3 陶粒混凝土材料力学性能指标Tab.3 Mechanical properties of ceramsite concrete

1.2 试件设计与制作

采用正交试验设计法设计了4个薄壁钢管陶粒混凝土轴心受压短柱试件。考虑柱端加劲肋板的影响后，试件的实际长径比在2.77～3.50[1]。以核心陶粒混凝土抗压强度、钢管壁厚为设计变化参数，各试件的设计参数见表4。

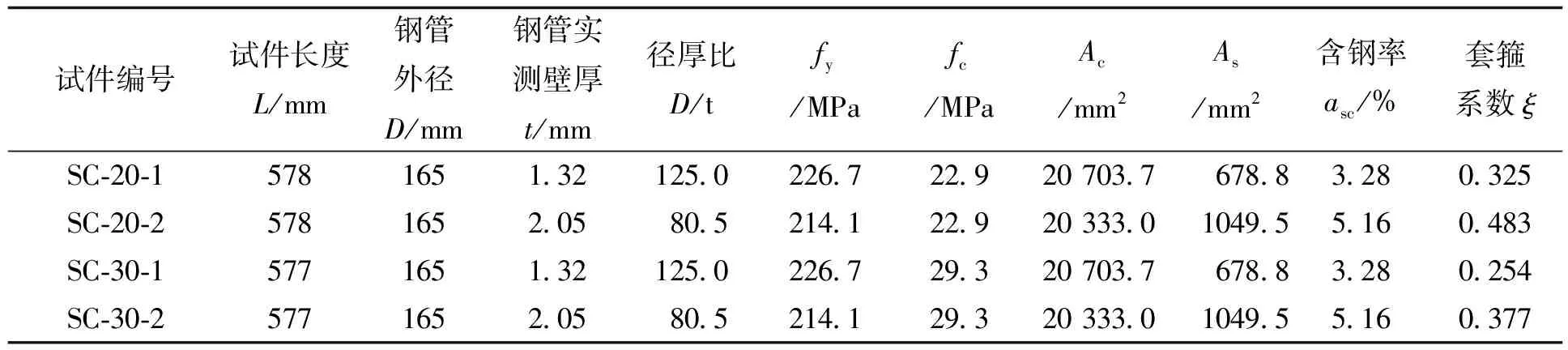
表4 试件设计参数表Tab.4 Designed parameters of specimens

加载试件时，为了使钢管与核心陶粒混凝土同时承压，试件两端焊接210 mm×210 mm×10 mm(厚)的方形Q235封堵钢垫板，并沿环向均匀焊接4片60 mm×60 mm×5 mm(厚)的直角三角形加劲肋板，以增强垫板和钢管的连接。试件的加工方法为：将钢管两端打磨平整后，先焊接一端封堵垫板和加劲肋板，然后将钢管竖向直立，从未封闭端分层浇筑陶粒混凝土，每层厚度取为钢管内径，插入钢棒振捣，当即将灌满时，留出10 mm找平段，待自然养护28 d后，以微膨胀水泥砂浆填充并抹平，养护2 d后，再焊接此端的封堵垫板和加劲肋板。

1.3 加载及量测方案

采用300 t电液伺服压力试验机对4根轴压柱试件进行单调静力加载试验。试验机的上、下承压钢板各布置2台电子位移计测定柱端两侧的位移量，以获得试件的压缩变形量和柱端微小转角。试件高度中点截面沿钢管外周环向均匀布置4对电阻应变片，分别测定钢管纵向应变和环向应变，试件加载方式和测点布置示意图如图1所示。

(a)试件加载方式

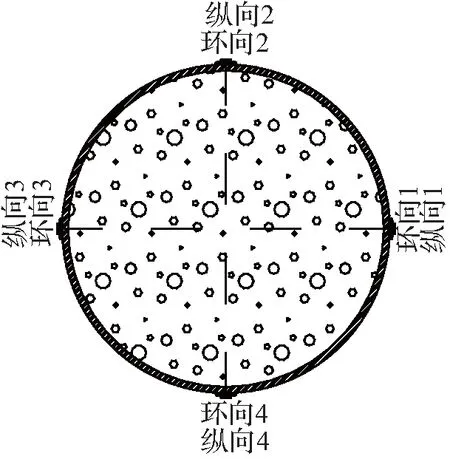
(b) 钢管应变测点布置示意图

正式加载前，先在弹性范围进行预加载，调整试件垂直度，直至环向4只纵向应变片的测值随荷载的增大而接近同步等幅变化，以确保试件处于轴心受压状态。正式加载时，钢管环向或纵向屈服前，荷载分级为每级20 kN；当钢管屈服后，降至每级10～15 kN；接近峰值荷载时，进一步降至每级5 kN。每级荷载停留2～3 min。当试件的抗压承载力降低至极限承载力的70%以下或纵向应变超过应变片量程(约为20 000 με)时，认为试件达到破坏，从而结束加载。

2 试验结果及分析

2.1 破坏过程及破坏形态

①由于采用竖向浇筑，密度较小的陶粒易上浮，导致试件上端密实度和强度较低，在加载到峰值荷载的50%(SC-20-1、SC-30-1)和80%(SC-20-2、SC-30-2)左右时，壁厚较薄的试件，会较早地在上端部50～100 mm处出现局部鼓曲的现象，并随荷载的增大而愈发明显。这一现象出现的早晚与钢管壁厚有关，与混凝土的强度等级基本无关；②柱子中段范围在达到峰值荷载之前，管壁较厚的试件SC-20-2和SC-30-2无明显鼓曲现象，说明此段受力较均匀，但管壁较薄的试件SC-20-1和SC-30-1在接近峰值荷载时，除柱两端区域出现较明显局部鼓曲外，柱高1/3处也出现小幅的局部鼓曲现象；③4个试件在加载至峰值荷载80%以上时，柱中截面钢管环向应变数据增大迅速，表明此时混凝土横向变形发展加快，同时可听到内部混凝土发出轻微的“啪啪”声；在达到极限承载力之前，除端部外，其余大部分区域钢管壁未出现明显不均匀变形；④达到峰值荷载后，试件轴向压缩变形随承载力的降低而显著增大，中间区段钢管壁出现多道环状褶皱。其中，试件SC-20-1和SC-30-1柱高中部钢管被核心混凝土胀裂，沿纵向直焊缝裂开，透过裂缝可以观察到该部位内部混凝土已被压碎。4个试件卸载后的最终破坏形态如图2所示。剖开钢管后，可观察到核心陶粒混凝土仅钢管褶皱处破碎严重，其余位置裂缝不明显，未出现斜剪裂缝，为腰鼓形破坏[18]，可见在薄壁钢管均匀约束下，陶粒混凝土可随钢管发生较大塑性变形，但因钢管壁厚小、陶粒混凝土弹性模量较低，薄壁钢管在陶粒混凝土软化后比普通钢管更易发生纵向屈曲而产生环状褶皱。

(a) SC-20-1

(b) SC-20-2

(c) SC-30-1

(d) SC-30-2

2.2 荷载-位移曲线

通过纵向位移计采集到的数据，得到各试件的荷载-位移关系曲线如图3所示。

图3 试件荷载-位移关系曲线 Fig. 3 Load-displacement relation curves of specimens

图3中各试件的初始一小段斜率较小，其原因是浇筑时陶粒上浮，柱顶附近的混凝土密实度相对较低，导致柱端在不大的荷载作用下变形量较大；但压缩变形达到1 mm左右后，曲线发生明显转折，斜率陡增，因此初始段为非正常曲线，不能真实反映试件的受力性能。此后的荷载-位移关系曲线可分为3个阶段：①第1阶段为弹性阶段，对应荷载低于峰值荷载的80%，纵向压缩变形与荷载近似成线性关系，轴向抗压刚度较大。与普通的钢管混凝土试件相比，薄壁钢管约束陶粒混凝土短柱轴压弹性极限与极限荷载的比值更大[1-3]；②第2阶段为弹塑性阶段，荷载进一步增至峰值，曲线斜率所代表的轴向压缩刚度不断降低，纵向压缩变形增长加快，试件表面钢管局部鼓曲逐渐明显；③第3阶段为达到峰值荷载后的下降段，轴向抗压刚度沿负向持续下降，但下降曲线并不陡峭，显示出较好的后期承载力和延性，试件表面多处可见明显鼓曲和褶皱，最后在柱高中点附近因横向泊松变形超过钢管约束能力而发生破坏。

对比4个试件的曲线可以发现：①与试件SC-20-1和SC-30-1相比，试件SC-20-2和SC-30-2的曲线上升段斜率和刚度较大，峰值荷载也较大，下降段相对较平缓，并出现拐点，说明增大钢管壁厚可提高轴压构件的轴向抗压刚度、极限承载力、后期承载力和延性；②同等条件下，试件的极限承载力随轻骨料混凝土强度等级的提高而提高，但对剩余承载力和延性的提高作用较弱；③破坏时，组合试件的最大纵向压缩应变远大于无约束陶粒混凝土的极限压应变(约为1 170～1 360 με[19])，说明薄壁钢管的约束作用可明显提高陶粒混凝土的变形能力。

2.3 荷载-钢管应变曲线

提取各试件4对测点应变值取平均，得到的试件荷载-钢管应变关系曲线如图4所示。

由图4分析可得：

图4 试件荷载-钢管应变关系曲线Fig. 4 Load-steel tube stain relation curves of specimens

①当荷载低于80%峰值荷载时，各试件的纵向、环向应变与荷载基本呈线性比例关系，此阶段的纵向应变相对于环向应变增长更快，说明此阶段核心陶粒混凝土的横向泊松变形小于纵向变形，钢管此时的约束作用较弱。环向应变与纵向应变之比在0.2～0.3的范围内，接近于普通钢材的泊松比0.3。

②当荷载超过峰值的80%时，钢管从弹性阶段过渡到弹塑性阶段。环向应变与纵向应变之比逐渐增大到0.5～1.0，说明此阶段核心陶粒混凝土的横向泊松变形逐渐接近纵向变形，混凝土的泊松比大于钢管的泊松比，使柱中截面的薄壁钢管对核心陶粒混凝土的约束作用逐渐增强。根据Von-Mises准则，钢管环向拉应力逐渐增大的同时，纵向压应力将减小，因此后续的荷载增量主要由核心陶粒混凝土承担。试件在此阶段仍能承受更大的荷载，原因是钢管的约束作用间接提高了核心陶粒混凝土的强度和相应的承载力，且承载力的提高幅度大于钢管纵向承载力的降幅。

③当荷载达到峰值时，峰值荷载对应的钢管纵向、环向应变均达到并超过5 000 με，大大高于无约束陶粒混凝土的峰值应变，由此可见，薄壁钢管的约束显著提高了陶粒混凝土的弹塑性变形能力。

④在达到峰值荷载、进入下降段后，钢管的纵向、环向应变增长加快，核心陶粒混凝土逐渐失效，钢管约束对其承载力的提高幅度已不能抵消钢管纵向承载力的降幅，因此试件承载力随之降低。在此阶段各试件多处产生鼓曲和环状褶皱，应变值出现波动，并有一定离散性，部分应变测点因位于褶皱处而较早失效。

⑤对比SC-20-1 和SC-20-2这2个试件的荷载-纵向应变曲线，SC-20-1的峰值荷载小于SC-20-2，但前者的峰值荷载对应的峰值应变更大；对比SC-30-1和SC-30-2也得到相似的规律，说明在同等强度等级的陶粒混凝土中，试件的受压承载力随着壁厚的增大而增大，但峰值荷载对应的纵向应变减小。

2.4 钢管泊松比分析

排除端部钢管局部屈曲的影响部分，钢管的环向应变可近似代表横向应变。本文定义“钢管的泊松比”为钢管外表面测得的环向应变εsc与纵向应变εsl之比。图5给出了试件SC-20-1和SC-20-2实测的荷载加载比例-钢管泊松比关系曲线。由图5可以看出，当荷载低于峰值荷载的0.8倍时，2个试件钢管的泊松比数值波动不大，基本稳定在0.22～0.28，不同测点钢管泊松比的差值在0.05以内；当荷载超过峰值荷载的80%后，曲线发生弯折，斜率大幅降低，变为水平夹角约为11°斜直线，泊松比随荷载迅速增大，钢管对核心陶粒混凝土的约束作用变得明显，此阶段4个测点的曲线差异不大，表明约束作用较为均匀。2个试件在峰值荷载对应的钢管泊松比分别为0.4～0.7和0.7～1.0，说明钢管壁厚较大时提供的约束作用更强。对比2个试件各测点曲线的离散程度可以看出，钢管壁厚较大的约束作用更均匀，较薄的钢管更易受局部屈曲的影响，离散性稍大。

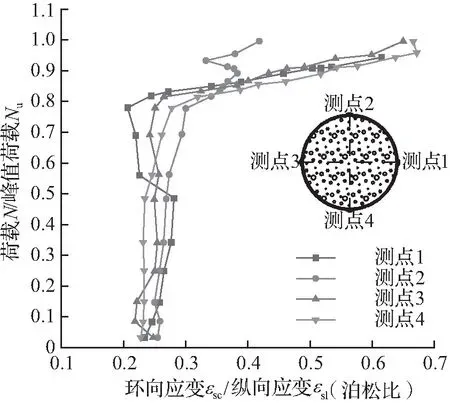
(a)SC-20-1

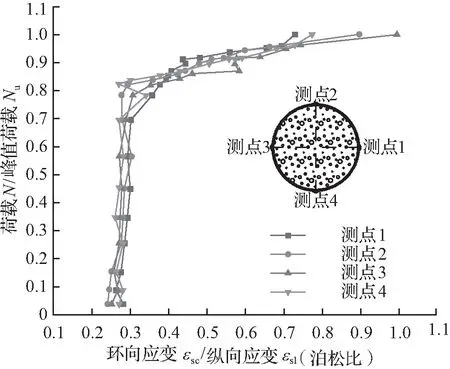
(b)SC-20-2

2.5 极限荷载分析

对于同等条件的无侧向约束的素陶粒混凝土柱，其轴压极限承载力计算值Nu=fcAc，可由表4中的fc和钢管内径Dcor计算得到。4个薄壁钢管约束陶粒混凝土试验柱与其相应的无约束素陶粒混凝土柱的轴压承载力比较见表5。

表5 试验柱与同条件无约束陶粒混凝土柱的轴压承载力比较Tab.5 Comparison on axial compression bearing capacity of specimens and unconfined ceramsite concrete columns

由表5可以看出：薄壁钢管陶粒混凝土柱的轴心受压承载力相较于无约束的素陶粒混凝土柱有明显提高，平均提高率为50%；增大钢管壁厚和提高核心陶粒混凝土强度等级均可提高柱子的轴压承载力，但前者的提高效果更为显著，且混凝土强度较低时提高率较大。其原因是试件的加载方式为钢管与核心陶粒混凝土共同承压，增大钢管壁厚能同时增大其自身的承压能力和抗屈曲能力，并提高其约束能力，故承载力提高效果更显著；而较高等级陶粒混凝土的弹性模量更高，脆性更大，横向泊松变形更小，故相同壁厚钢管的约束效果相对降低。

2.6 陶粒混凝土抗压强度提高系数与套箍系数关系分析

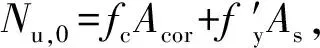
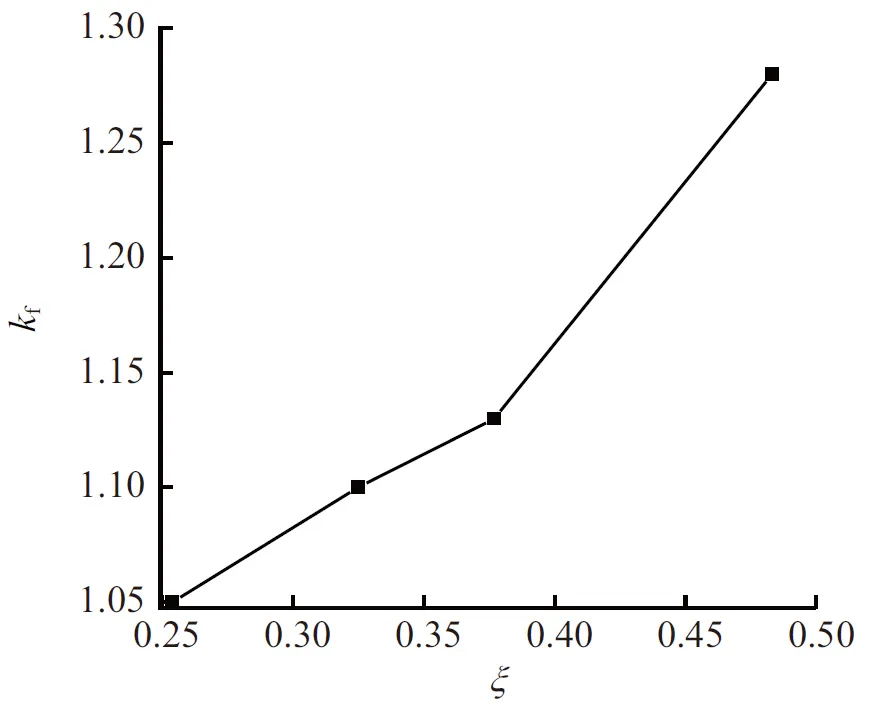
图6 陶粒混凝土抗压强度提高系数kf-套箍系数ξ关系曲线 Fig.6 Compression strength increase coefficient-confinement parameter relation curves of theceramsite concrete

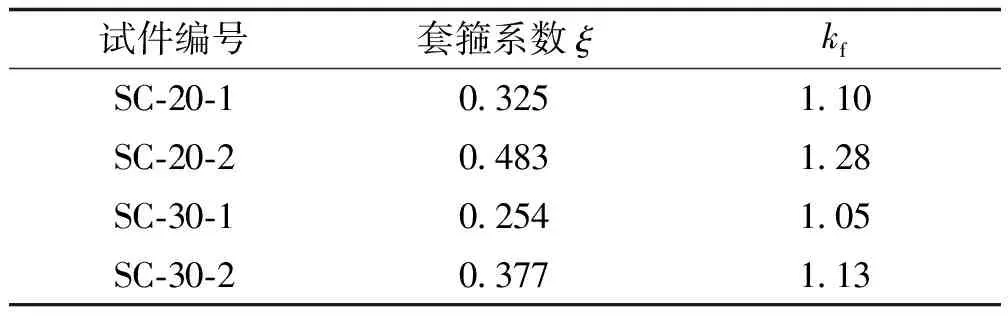
表6 试件的陶粒混凝土抗压强度提高系数kfTab.6 Compression strength increase coefficient kf of ceramsite concrete of specimens

由表6可以看出，试件的强度提高系数在1.05～1.28，说明约束对陶粒混凝土强度的提高作用有限，其原因是陶粒较脆，陶粒混凝土弹性模量较低，纵向变形较大，钢管壁厚较薄，对横向变形约束有限。由图6可见，抗压强度提高系数kf与套箍系数ξ成正比关系。

2.7 延性分析

以位移延性系数衡量试件的延性，取柱子整体的轴向压缩变形量作为位移。位移延性系数μD所需的屈服位移Dy根据荷载-位移曲线由能量等值法确定，极限位移Du取为荷载-位移曲线下降段荷载等于85%峰值荷载时对应的位移。4个试件的位移延性系数详见表7，位移延性系数-套箍系数关系曲线如图7所示。

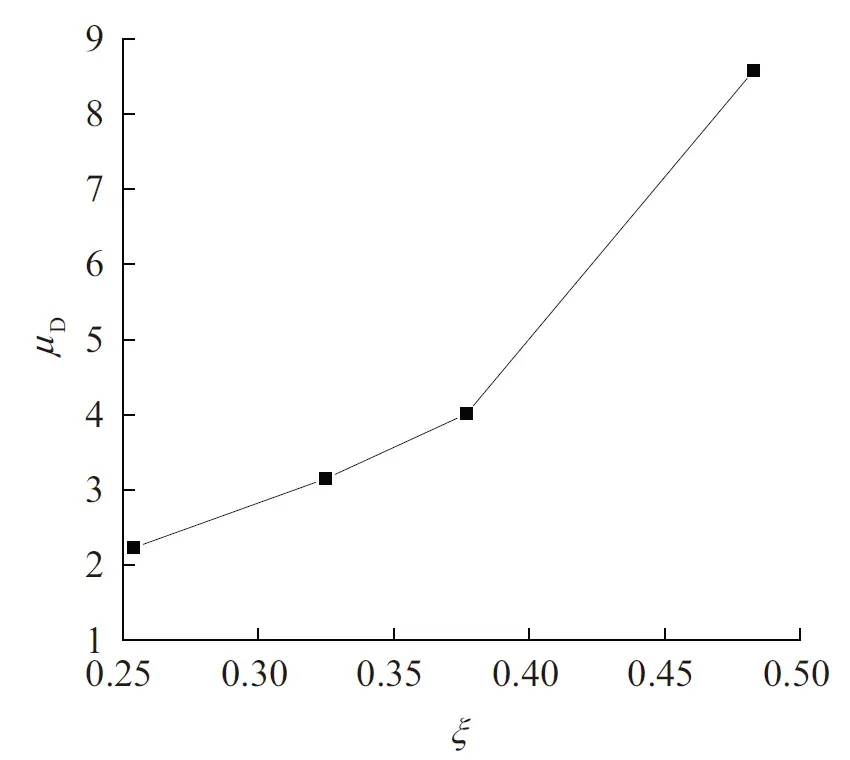
图7 位移延性系数μD-套箍系数ξ关系曲线Fig.7 Displacement ductility coefficient-confinement parameter relation curve

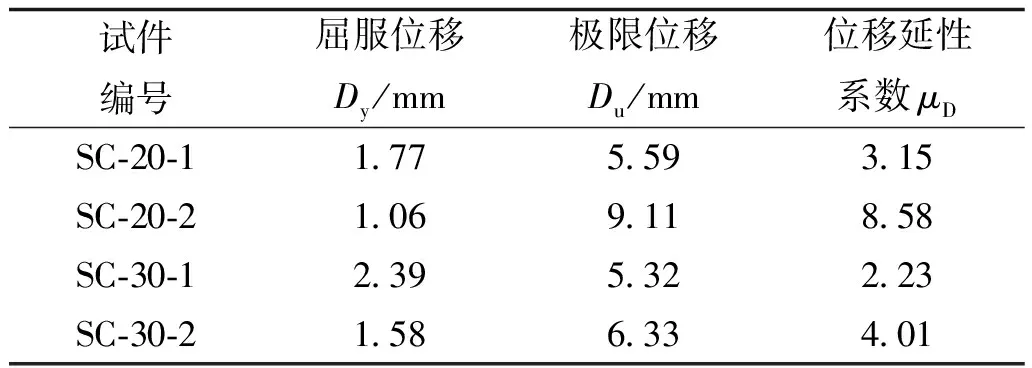
表7 试件位移延性系数计算结果Tab.7 Calculation results of displacement ductility coefficients

由表7和图7可以看出，多数试件的延性较好，位移延性系数与套箍系数成正比，钢管壁厚较大时可提供较强的约束，对应的延性系数较大，但采用过薄的钢管约束强度等级较高的陶粒混凝土时，所得的延性系数反而较小。当钢管壁厚相同时，强度等级较高的陶粒混凝土因弹性模量较大，脆性增大，变形能力降低，对应的延性系数也有所减小。

3 结论

① 薄壁钢管陶粒混凝土轴心受压破坏过程可分为3个阶段：荷载小于80%峰值荷载为弹性阶段； 80%～100%峰值荷载为弹塑性阶段；峰值荷载过后为下降段。下降段较为平缓，后期承载力较高。

② 峰值荷载之前，柱中段钢管未出现明显局部屈曲，达到峰值荷载后，柱中段钢管多处局部屈曲逐渐明显，并最终发展为环状褶皱，因此薄壁钢管陶粒混凝土必须重视钢管屈曲对极限承载力的影响，建议采用钢管内设置纵向肋板、管外增设环箍的方式提高薄壁钢管的稳定性和刚度，并保证内部混凝土的密实度。

③ 径厚比为80～125的薄壁钢管仍能提高陶粒混凝土强度、刚度和塑性变形能力，套箍系数在0.25～0.48时可使陶粒混凝土的抗压强度提高5%～28%，强度等级较低的陶粒混凝土的抗压强度提高率较高，抗压强度提高率与套箍系数成正比。

④ 与同条件的素陶粒混凝土柱相比，薄壁圆钢管约束陶粒混凝土短柱的轴压性能较好，轴压承载力可提高30%以上，平均提高50%，提高率与钢管壁厚、陶粒混凝土强度等级成正比，但增大壁厚的提高效果更显著。

⑤ 薄壁钢管陶粒混凝土轴压构件的延性总体良好，压缩变形延性系数接近和超过3.0，延性系数与套箍系数成正比，延性随钢管壁厚的增大而提高，但随陶粒混凝土强度等级的提高而降低。

管内增设纵肋、管外增设环箍对柱子轴压性能的影响规律及纵肋、环箍的设计参数取值仍需更进一步的试验和理论研究。