面向OFDM-MFSK水声通信的差错控制方法

高 潭, 吕成财, 田 川,*

(1. 中国科学院深海科学与工程研究所, 海南 三亚 572000; 2. 中国科学院大学, 北京 100049)

0 引 言

水声通信技术是唯一可靠的远距离水下无线通信手段,可以实现各类水面和水下工作平台的信息交互,具有重要的研究价值。而水声作为一种特殊的信息载体,其信道带宽窄、噪声高、时变特性明显,且常伴随着严重的多径衰落和多普勒效应,不利于水声信号的检测和解调,会严重影响水声通信的效率。由于以上因素的影响,现有的水声通信系统大多功耗较高,且需要采用复杂的信道估计及均衡算法,使得水声通信设备的造价普遍高昂。例如,在由多个定位信标构成的水声通信定位系统中,实现定位算法所需的通信速率较低,但因其需要使用多个水声通信设备,定位系统的实现同样需要较高成本。此外,由于成本问题,如传感器等数据量小、布放量大的水下设备通常不使用水声通信传送数据,而是用传输线与各类水下和水面工作平台相连接,此类平台的布放与回收同样需要花费较多的人力物力。由此可见,低成本水声通信设备仍有较大的研发价值和潜力。

正交频分复用(orthogonal frequency division multiplexing, OFDM)是一种多载波技术,能有效降低多径衰落的影响,在水声通信领域有非常广阔的应用前景。使用调制方式为多进制频移键控(multiple frequency shift keying, MFSK)的OFDM通信系统称为OFDM-MFSK,能使OFDM系统在保留上述优点的同时兼具MFSK调制特有的稳健性和抗相位噪声的能力,降低了系统对信道估计和均衡的需求,从而能以较低的硬件成本实现数据的可靠传输。此外,相比其他调制方式,使用MFSK调制的OFDM信号带有较多的空子载波。可以利用这些空子载波在频域的分布来估计水声信道的多普勒频移,从而对信号进行多普勒补偿,进一步提升通信的可靠性。

由于基本的OFDM-MFSK调制中子载波的相位不携带信息,文献[17]中提出一种改进方法,通过在MFSK的基础上对子载波的相位进行多进制相位键控(multiple phase shift keying, MPSK)调制以利用其相位携带数据,提高了系统的频带利用率。然而,使用相位调制的OFDM水声通信系统并不稳定,在多径较为严重或同步不精确时其可靠性会明显下降。为了保证通信的可靠性,仍需要引入复杂的信道估计及均衡算法,并结合信道编码以提升通信的效率,大幅提升了系统的软硬件设计成本。

此外,目前广泛应用于无线电通信中的信道编码如喷泉码、低密度奇偶校验码等虽然能有效地提升通信的可靠性,但均要求较长的码字长度,应用于低速水声通信系统时,接收端通常不能即时译码,会极大地影响通信的实时性。因此,出于对通信的实时性和硬件成本考虑,低速水声通信系统如水下传感器网络等仍常采用里所码、BCH码等编码方式作为信道编码。

为了在充分利用OFDM系统带宽资源的同时兼顾数据传输的可靠性和实时性,本文提出了一种差错控制方法,在以OFDM-MFSK信号传输原信息序列的基础上,使用MPSK调制传输冗余编码,使得接收端可以选择性地结合两路数据以减少信息序列中的错误。在信道条件较差的情况下接收端仍可选择性地舍去信号的相位信息,以保证系统的可靠性。同时,此种差错控制方法所使用的编码码长短,发送端可仅用一个OFDM符号传输多个完整的码字,便于接收端的实时译码,从而保证低速水声通信系统的实时性。

本文的第1节主要介绍了OFDM-MFSK水声通信系统的模型以及OFDM-MFSK-MPSK的实现原理。第2节中给出了所使用的线性分组编码和纠错算法,并结合实例逐步讲述了编码、校验、纠错的实现过程。第3节为仿真实验结果,分析比较了在算法与不同校验码结合后的纠错能力和此算法在多径衰落信道下对OFDM-MFSK-MPSK系统可靠性的提升,并统计了纠错算法所需的运行时间和误比特率(bit error rate, BER)之间的关系。

1 OFDM-MFSK水声通信系统模型

1.1 OFDM-MFSK

OFDM-MFSK即将OFDM的子载波分成若干组,每组子载波构成一路独立的MFSK信号。在采用傅里叶逆变换的OFDM系统中,各个子载波的调制可以分为映射和傅里叶逆变换两部分。一个典型的OFDM-MFSK水声通信系统结构的实现框图如图1所示。以OFDM-2FSK信号为例,其在频域上的调制示意图如图2所示。

图1 OFDM-MFSK水声通信系统结构Fig.1 Structure of OFDM-MFSK underwater acoustic communication system

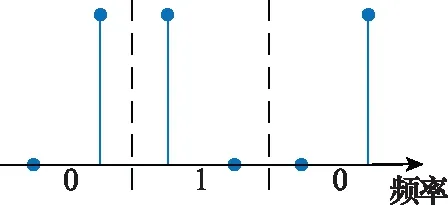
图2 OFDM-2FSK调制频域示意图Fig.2 Schematic diagram of OFDM-2FSK modulation in frequency domain

设OFDM-MFSK共有×个子载波被分成组,则信号的时域波形可表示为

(1)

式中:()是窗函数;为第组子载波经MFSK调制之后确定出的载波频率。设为第组子载波传输的比特位,OFDM信号中频率最低的子载波中心频率为相邻子载波的频率间隔为Δ,则可表示为

=+[(-1)+]Δ

(2)

OFDM-MFSK水声信号在接收端通常采用非相干方式解调,在免去复杂的信道估计和均衡的同时仍有较好的准确度,能显著降低水声通信系统的软硬件开发成本。然而由于OFDM-MFSK调制的带宽利用率显著低于其他调制方式,在带宽有限的水声信道中的有效性并不理想。

1.2 OFDM-MFSK-MPSK

由上述OFDM-MFSK原理可知,OFDM-MFSK信号的相位不携带信息,因此可以在OFDM-MFSK信号的基础上调制各个有效子载波的相位以携带额外的数据,从而进一步地提高频带利用率。设OFDM-MFSK信号的第组子载波的相位为,则式(1)中的信号添加相位信息后可以表示为

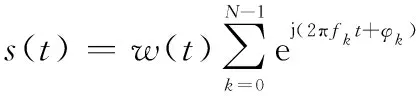
(3)

OFDM-2FSK-2PSK调制信号的频域示意图如图3所示。

图3 OFDM-2FSK-2PSK调制频域示意图Fig.3 Schematic diagram of OFDM-2FSK-2PSK modulation in frequency domain

通过OFDM-MFSK-MPSK系统,OFDM信号可以复合使用频率键控和相位键控分别调制两路不同数据,极大地提升了传输效率。然而在实际应用中,由于两种调制方式对衰落和相位噪声的敏感度差异较大,接收端解调后的两路数据很可能会有不同的误码率。在极端情况下,相位调制的可靠性不能满足数据传输的需要,此时就需要收发端重新协调更换传输方式,因而会大幅提高系统所需的协议开销。

2 基于OFDM-MFSK的差错控制编码

2.1 添加冗余编码的OFDM-MFSK-MPSK系统结构

为了在充分利用相位调制带来的额外信道容量的同时进一步简化系统设计,使其具有更高的可靠性,在此提出一种基于OFDM-MFSK-MPSK的前向纠错策略,其原理图如图4所示。基本思想是对原数据进行冗余编码,MFSK调制仍传输原码,冗码部分则由MPSK调制传输,接收端结合两路信息即可完成前向纠错。在相位调制的可靠性较低时,接收端也可以直接对接收信号MFSK解调得到原码以保证系统的稳健性。

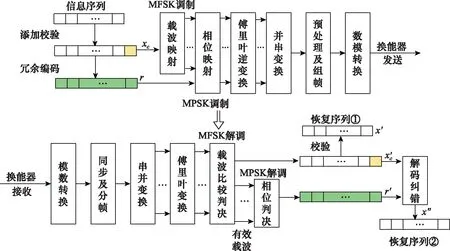
图4 基于OFDM-MFSK-MPSK的差错控制算法实现原理Fig.4 Implementation of error control algorithm based on OFDM-MFSK-MPSK

2.2 一种短码长的线性分组编码

按第1.1节中所述方式复合使用MFSK和MPSK调制构建OFDM信号时,若两种调制方式阶数相同,则两调制方式所传输信息序列的比特位数也相同。据此构造一种[2,]线性分组码,使此种编码中每个码字的冗余位和信息位的长度相同,以便分别用两种调制方式并行发送。此种编码方式得当生成矩阵和校验矩阵可表示为=[],=[],其中各矩阵如下所示：

(4)

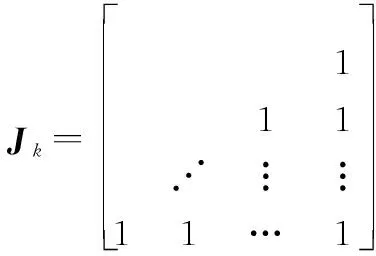
(5)

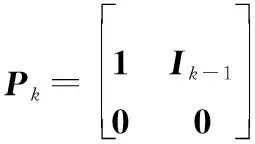
(6)

式中：为阶单位矩阵。设个待编码比特构成的向量为=[,, …,-1],则编码过程可表示为=[,]。其中[,]为发送比特构成的行向量,=[,, …,-1]即为编码得到的冗余位。

假设发送的信息序列为,接收端收到的信息序列表示成的行向量为,误比特构成的向量为=[,, …,2-1],根据各向量之间的关系可得

=+

(7)

(8)

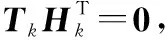
(9)

注意到此种编码在大于等于3时,其最小码距始终为3,与的取值无关。为了降低码字长度和编解码的计算复杂度,选取构成矩阵的最小阶数=3构成矩阵,则有编码矩阵和校验矩阵如下：

(10)

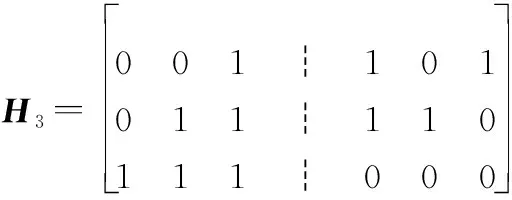
(11)

由式(3)可见阶矩阵的秩为-1,因而冗码=[,, …,-1]的集合只包含2-1种码字。当=3时所有的冗码码字均在表1中示出。例如,3位比特[1, 0, 1]经2FSK调制发送,对应子载波上使用2PSK调制发送的冗码信息序列应为[0, 1, 1]。而接收端如果改用差分相移键控(differential phase shift keying, DPSK)方式解调,得到的2位差分码应为[1, 0]。如表1中所示,由于表1中冗码的4种码字之间均有两位比特不同,接收端可以统计接收冗码码字中不属于此4种码字的个数,据此估算出MPSK解调的误码率。此外,每种冗码码字与其差分码之间存在一一对应关系,因而接收端在多径衰落严重或同步定时存在偏差的情况下同样可以使用频域DPSK解调,再将解调结果对照表1得到对应的冗码以对抗相位模糊。

表1 码字与不同解调方式的对应关系

2.3 基于线性分组编码的校验

基于第2.1节和第2.2节中所述系统结构和编码,为了提升系统的可靠性并在接收端仅使用MFSK解调的情况下仍能有基本的检错能力,需要预先在信息序列添加其他校验,如奇偶校验、循环冗余校验(cyclic redundancy check, CRC)等,再与第2.2节中所述线性分组码级联构成一个校验块。为保证接收端的译码效率和检错能力,上述校验码的码字长度取较小值为宜。校验长度与译码复杂度和纠错能力的关系见第2.4节算法复杂度分析和第3节中仿真结果。

此外，可以通过统计校验结果中与表1不相符的编码分别估计出接收端MFSK和MPSK解调结果的BER。

设发送信息序列为[001110101],分组编码前添加4位奇偶校验码,以OFDM-2FSK-2PSK调制为例,数据的编码、调制过程可以表示为图5。编码前首先将待发送数据分为3比特一组,再计算出3组比特的垂直奇偶校验码,作为最后一组比特添加至序列末尾。随后每组比特各自左乘编码矩阵得到包含冗码的完整编码校验块。校验块中包含奇偶校验的原码经2FSK映射,再与块中对应的冗码的2PSK映射结果相乘,最后进行OFDM调制成为一路OFDM-2FSK-2PSK信号发送到水声信道中。

图5 信息序列[001110101]的编码及调制过程Fig.5 Coding and modulation process of information sequence [001110101]

信号接收后的校验过程如图6所示。接收端在收到包含标红误比特的分组后,每组编码均按式(8)计算出对应的3位校验子。如果该组计算出的所有校验子中包含至少一个1,则可认定此组校验块中含有错误。至此接收端依据线性分组码的特性完成第一次校验。

图6 接收端分组校验过程Fig.6 Process of receiver packing and verification

2.4 基于错误图样前向纠错算法

如图7所示,根据式(7)将图6中计算出的校验子添加至的右侧构成模二增广矩阵,求解矩阵所表示的模二线性方程组即得到该组编码所有可能的2=8个错误图样。为简化搜索过程,只保留8个可能错误图样中误比特数不多于的结果作为备选。图7中的取值为2。

图7 错误图样的计算及纠错过程Fig.7 Error pattern calculation and error correction process

组合所有备选错误图样构成不同的校验块,筛选出其中满足奇偶校验者,作为校验块的纠错图样。最后将接收码组与纠错图样对位异或运算即可完成前向纠错。

设接收端共收到组校验,每组校验中含个[6,3]线性分组码的信息位。当接收到的数据中没有错误或只有少量误比特稀疏分布于信息序列中时,由于大部分校验子为0,需要搜索的组合数量较少,算法的时间复杂度仅为(),且更易得出正确的错误图样从而实现完全纠正。在接收码组中含有大量误比特的最差情况下,需要搜索的组合数量会大幅增加,算法的时间复杂度为(),其中与保留图样的误比特数阈值有关,当只保留误比特数不多于2个的结果时=3。此时搜索空间中满足奇偶校验的组合数量可能不唯一,完全纠错的可能性降低,纠错算法的效率将进一步下降。在第33节中仿真计算了使用不同校验码的纠错算法所需的运行时间与BER的关系。

3 仿真实验验证

3.1 使用不同校验的纠错算法性能分析

基于Matlab平台模拟搭建一条加性高斯白噪声信道以验证文中策略对OFDM-MFSK-MPSK系统可靠性的提升。设置OFDM信号脉宽50 ms,带宽4 kHz,共200个子载波,相邻子载波频率间隔Δ=20 Hz,采样率为100 kHz。信道中添加高斯白噪声。根据第2节中的编码及纠错算法,分别使用不同长度的奇偶校验码和CRC码与分组编码级联,设置为3，运行纠错算法,统计纠错后的BER并与未编码系统相比较。仿真得到OFDM-MFSK-MPSK系统在为2和4时,使用不同校验的编码的BER随信噪比变化分别如图8(a)和图8(b)所示。

图8 应用纠错算法前后BER随信噪比变化Fig.8 BER with the signal-to-noise ratio before and after applying the error correction algorithm

根据仿真结果可见,在加性高斯白噪声信道下,调制阶数为2和4的OFDM-MFSK-MPSK系统应用纠错算法后均能降低接收端的BER。纠错算法的性能与校验长度负相关,使用4位奇偶校验码的纠错算法有最强的纠错能力,在两种调制阶数的系统中其编码增益分别可达5 dB和4 dB。使用含有其他校验码纠错算法的系统所获得编码增益同样可达3 dB以上。

3.2 多径水声信道仿真分析

为研究文中差错控制算法在多径水声信道下对的OFDM-MFSK-MPSK系统可靠性的提升,基于Matlab平台搭建了两条多径衰落信道,其单位冲激响应分别如图9(a)和图9(b)所示。图9(b)所示的信道B中多径分量具有更高的能量占比。

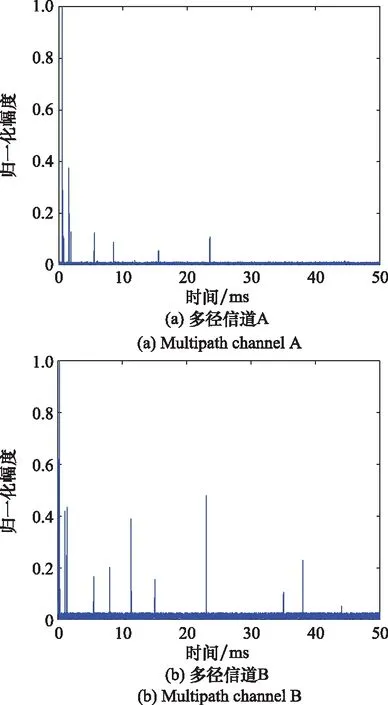
图9 两条多径水声信道的单位冲激响应Fig.9 Unit impulse responses of two underwater communication channels

信号采用OFDM-4FSK-4PSK调制方式,设置信号脉宽50 ms,带宽4 kHz,共200个子载波,相邻子载波频率间隔Δ=20 Hz,采样率为100 kHz。纠错算法使用4位奇偶校验码作为校验,设置为3,分别统计两条信道下应用纠错算法及编码前后接收信号的BER,并仿真计算相同信道下无编码的OFDM-4FSK系统的BER作为对照。图9中两条信道下的仿真结果分别如图10(a)和图10(b)所示。

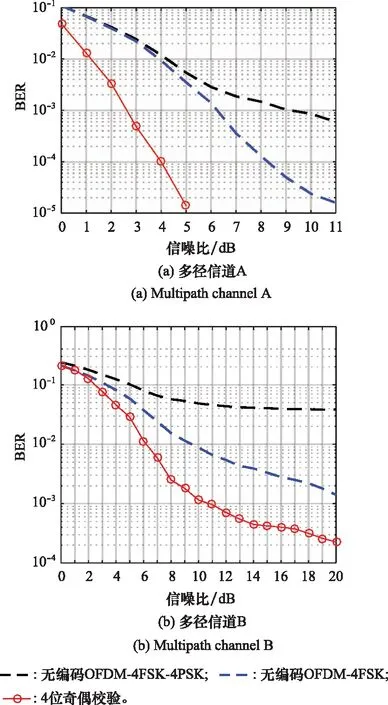
图10 两种多径信道下应用纠错算法前后BER随信噪比变化Fig.10 BER with the signal-to-noise ratio before and after applying the error correction algorithm under the two multipath channels

由图10可见,未编码的情况下,两条多径信道下引入了相位调制的OFDM-4FSK-4PSK信号的可靠性均低于OFDM-4FSK信号。编码及纠错算法的性能总体上受信道衰落程度的影响,然而在添加编码并应用纠错算法之后,两条信道下OFDM-4FSK-4PSK调制所传输信息序列的可靠性均有大幅提高,可将BER降低两个数量级以上,明显优于未编码的OFDM-4FSK调制。

3.3 纠错算法时间随BER变化

为研究校验长度不同时纠错算法复杂度与BER之间的关系,选取长度为4到6的奇偶校验分别与分组码级联组成校验块,发送编码前长度为1.2 Mbit的信息序列,再将均匀分布的误比特添加到编码后的两路序列中。接收端运行纠错算法处理两路序列,统计每次运行所需要的时间。仿真得到在取2和3时,不同奇偶校验长度下,算法的运行时间与接收到信息序列中BER的关系如图11(a)和图11(b)所示。

由仿真结果可见,纠错算法的运行时间会随着接收信息序列中BER的降低快速下降,因而算法在BER较低的情况下有着更高的效率。

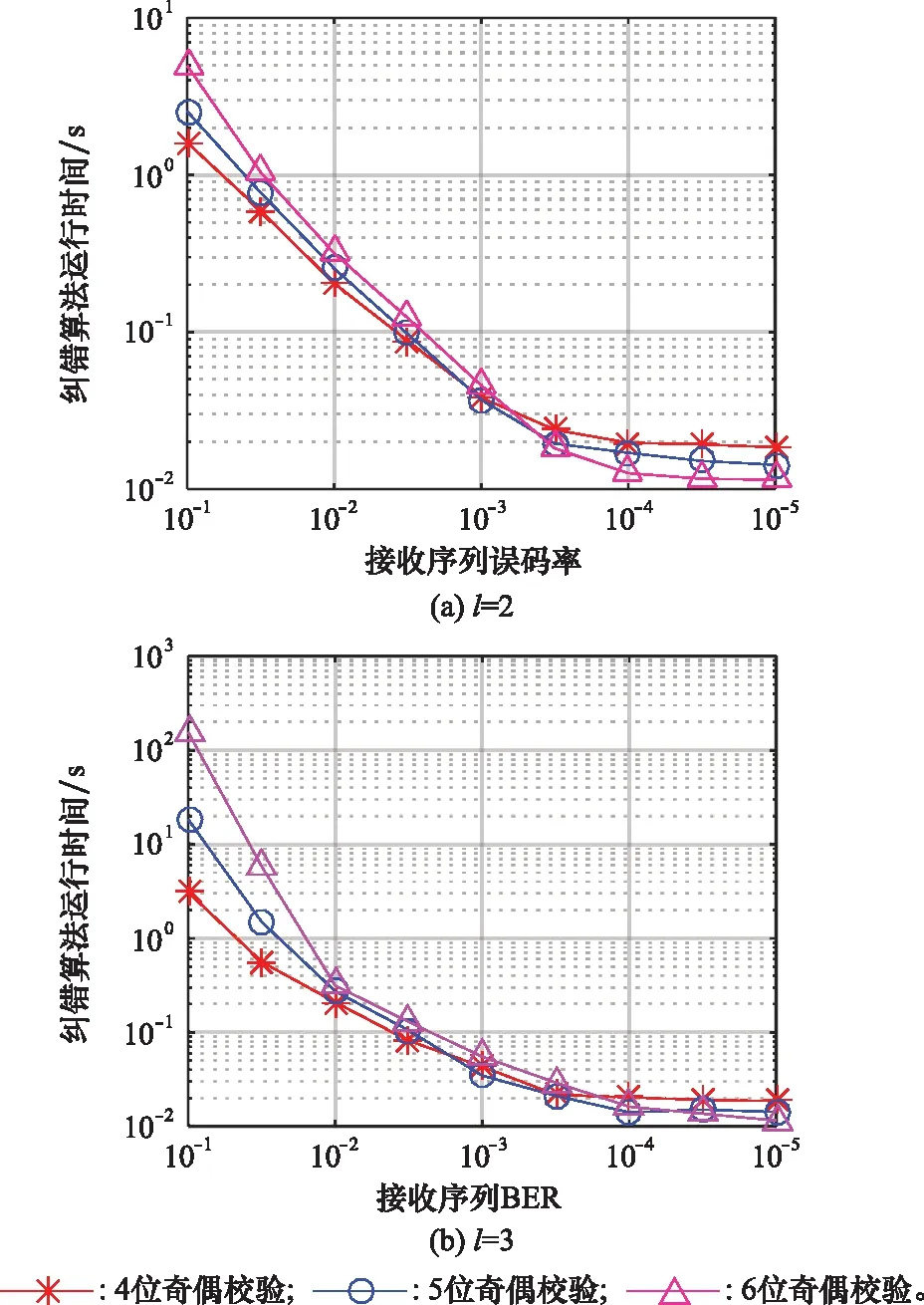
图11 纠错算法运行时长随BER变化Fig.11 Running time of the error correction algorithm with BER

4 结 论

本文基于OFDM-MFSK水声通信系统架构提出了一种差错控制方法,其实现原理可分为信号的复合调制和纠错算法两个部分。其中复合使用的OFDM-MFSK-MPSK调制方式能在不影响MFSK所调制数据的基础上利用MPSK调制额外传送一路信息序列,而纠错算法则能根据这一路额外的信息序列实现接收数据的校验和前向纠错。在信道条件较差时,相位调制的可靠性下降时,接收端仍能仅对使用MFSK解调得到完整的信息序列,并根据估算出的BER,选择性地结合相位信息进行纠错,保证了纠错算法在衰落信道下的有效性。

经仿真实验验证,在加性高斯白噪声信道及多径衰落信道中,本文所设计的编码及纠错算法均能有效降低OFDM-MFSK-MPSK系统的BER,且算法运行时间会随BER的降低快速收敛。

此种编码方式码长短、频带利用率高、编解码复杂度低,结合OFDM-MFSK水声通信系统免信道估计的特点,能在保证传输数据实时性和可靠性的同时有效降低水声通信系统的成本,适用于低速水下通信设备的设计。