基于修正小波变换插值-TAN的雷达降水粒子分类

李 海, 白 锦, 孙 研, 任嘉伟

(中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300)

0 引 言

降水粒子分类的研究在很多领域都有关键的指导意义。识别不同类型的降水粒子对研究粒子的微物理特性极其重要,降水粒子的精确分类对天气预报、危险预警等也有极其重要的参考价值。双偏振天气雷达作为新型天气雷达,常被用来探测降水目标,其与常规天气雷达相比,可以获得除降水粒子回波强度外的其他各种偏振参量。不同的偏振参量可以反映不同的降水粒子信息,利用这些信息可以更好地实现降水粒子的检测。

高分辨率的双偏振气象雷达获取的目标回波对天气过程的描述更加精细,可以获得更准确的气象数据,故可以提高降水粒子的探测精度。要提高双偏振气象雷达距离分辨率和方位分辨率,可以采用扩大天线直径或者是扩大发射信号带宽的方法,但此类做法需要对雷达天线、发射机等硬件进行改造,由此会带来改造成本高、改造时间长等问题。目前，地基气象雷达在远距离工作时会因波束展宽导致获得分辨率低的雷达数据;星载气象雷达虽可提供较大范围的降水观测,且不易受波束阻挡的影响,但其时空分辨率较低;因此探究如何在数据分辨率比较低的情况下提高降水粒子探测精度依然是值得研究的课题。

针对低分辨率数据,常用的插值算法包括线性插值算法与非线性插值算法。线性插值方法通常会对分布不平滑的数据有均衡化影响,会对数据高频信息造成损失,而非线性插值方法在一定程度上会改善这种缺陷,这当中比较多见的非线性插值方法是基于小波变换的插值方法。目前插值方法中基于小波变换的插值方法在图像插值方面应用颇多,但很少涉及雷达数据处理中的应用。

基于统计决策的降水粒子分类方法、基于模糊逻辑的降水粒子分类方法、基于支持向量机等的降水粒子分类方法是目前常见的应用于各个领域的降水粒子分类方法。其中模糊逻辑方法是当前被广泛使用的分类方法,而基于机器学习的降水粒子分类方法是近几年的研究热点。利用隶属函数来综合评定偏振参量是模糊逻辑法的特点,这种方法可以避免分类阈值的设定,故比传统统计模式识别方法的分类精度高。但此方法通常将权威研究者在各种不同情形下总结的经验值作为模糊逻辑隶属函数的相关参数,所以当环境变化时分类结果会有较大的不稳定性。在现有的众多分类算法中,贝叶斯算法因为能综合各种先验信息和有效利用数据样本信息成为当下机器学习领域的研究热点之一。何伟等应用朴素贝叶斯算法于预测降雨量,模型预测精度与目前的短期气候预测精度比有明显提高。郭雅芬等运用贝叶斯分类法预测中尺度对流系统的移动路径。刘虹利等利用贝叶斯方法对降水空间的插值模型进行改进,以提升插值精度。

针对低分辨率雷达偏振参量数据的降水粒子分类问题,本文提出一种双偏振气象雷达体制下基于修正小波变换插值-树扩展朴素贝叶斯(tree augmented naive Bayesian, TAN)的降水粒子分类方法,这种方法可以提高数据分辨率,也可以做到对各种不同类型的降水粒子进行分类。首先需要通过修正小波变换插值算法对原始低分辨率雷达偏振参量数据进行插值处理以获得插值后的高分辨率偏振参量数据;其次针对得到的高分辨率偏振参量数据再做进一步离散化操作,并利用得到的离散化数据进行TAN网络的结构和参数训练以获得最佳的TAN降水粒子分类网络;最后,使用TAN分类网络对修正小波变换插值后的高分辨率雷达偏振数据进行降水粒子分类。此方法在数据插值时可以保留更多高频信息,且在构造TAN网络时是通过对数据样本进行训练的方式得到网络参数的,所以即使数据采集条件发生变化，也可以重新对数据进行相应的操作,故比模糊逻辑方法的分类效果更稳定。

1 修正小波变换插值-TAN算法

本文所提修正小波变换插值-TAN算法的整体思路为:首先将修正小波变换插值应用到低分辨率雷达数据以获得高分辨率的雷达数据,然后利用获得的高分辨率雷达数据进行TAN网络结构和参数训练,最后将训练好的TAN网络用于高分辨率雷达数据的降水粒子分类。下面对所提方法进行具体论述。

1.1 修正小波变换插值方法

本文中修正小波变换插值方法首先对原低分辨率偏振参量数据进行双线性插值得到双线性插值后高分辨率偏振参量数据。然后对进行小波变换,得到其对应的低频分量数据与高频分量数据。这时, 低频分量数据近似等于原低分辨率偏振参量数据,则由除以可求得修正参数矩阵。考虑到各个分解部分之间具有相似性,利用求得的修正参数矩阵对高频分量数据做同样的修正,可得到修正高频分量数据。最后由原低分辨率偏振参量数据替代修正低频分量数据,与修正高频分量数据一起经过小波逆变换得到所需的修正小波变换插值后的高分辨率偏振参量数据。该方法的示意图如图1所示。

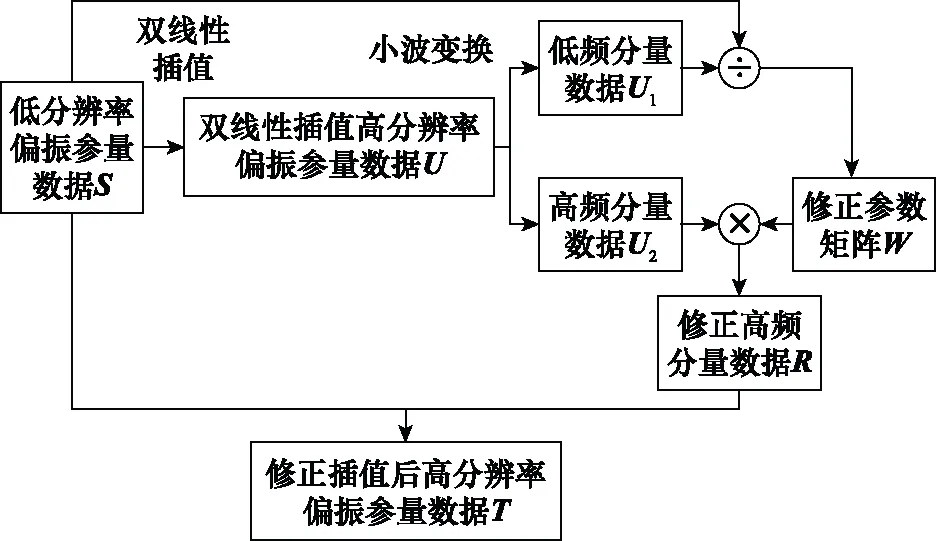
图1 修正小波变换插值方法示意图Fig.1 Schematic diagram of modified wavelet transform interpolation method

图1中,符号÷为除法符号,表示(,)除以(,),即用数据矩阵的第行第列元素除以数据矩阵的第行第列元素,相应得到数据矩阵的第行第列元素;符号×为乘法符号,表示(,)乘以(,),即用数据矩阵的第行第列元素乘以数据矩阵的第行第列元素,最后得到数据矩阵的第行第列元素。

下面以雷达偏振参量中的反射率因子为例(其他偏振参量同理),对修正小波变换插值方法具体过程进行介绍。

(1) 计算低频分量数据矩阵_high_(×)与高频分量数据矩阵_high_(×)

假设反射率因子的低分辨数据矩阵为行列的矩阵_low(×),对其进行双线性插值可得到插值后高分辨率数据矩阵_high(×2)。

根据小波变换的mallat算法进行信号的分解与重构。对数据矩阵_high(×2)按行进行小波变换,()表示数据矩阵_high(×2)的第一行数据, 其信号分解公式如下：

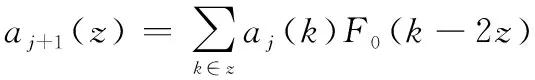
(1)

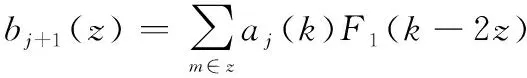
(2)

式中：+1()和+1()分别表示离散信号()经分解后得到的低频成分与高频成分；()和()分别表示低通滤波器和高通滤波器对应的滤波系数。 按照式(1)和式(2)对_high(×2)的每一行数据进行信号分解,每一行的低频成分组合即可得到低频分量数据矩阵_high_(×),每一行的高频成分组合即可得到高频分量数据矩阵_high_(×)。

(2) 计算修正参数矩阵_(×)

修正参数矩阵_(×)实际上是由双线性插值后高分辨率数据的低频分量数据矩阵_high_(×)计算原低分辨率偏振参量数据矩阵_low(×)时所需的系数矩阵。修正参数矩阵_(×)可用下式进行计算:

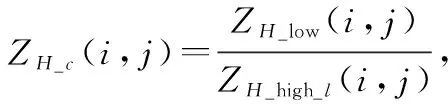
(3)

(3) 计算修正高频分量数据矩阵_high_(×)

因为小波分解过程中各个分解部分间具有相似性,根据此性质,利用修正参数矩阵_(×)与双线性插值后高分辨率偏振参量数据的高频分量数据矩阵_high_(×)可以计算得到修正高频分量数据矩阵_high_(×),计算公式如下:

_high_(,)=_(,)×_high_(,)，=1,2,…,;=1,2,…,

(4)

(4) 计算修正小波变换插值后的高分辨率反射率因子数据矩阵_new(×2)

根据小波变换mallat算法的信号重构公式,如下所示：

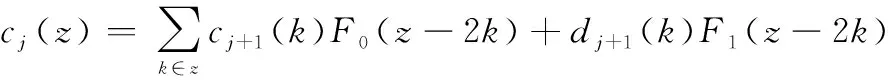
(5)

对原低分辨率偏振参量数据矩阵_low(×)和修正高频分量数据矩阵_high_(×)按行进行小波逆变换,即可得到最终修正小波变换插值后的高分辨率反射率因子数据矩阵_new(×2)。其中，+1()和+1()分别表示数据矩阵_low(×)和数据矩阵_high_(×)的第1行的数据;()表示小波逆变换得到的数据矩阵_new(×2)的第1行数据,对其他行数据同样按照式(5)进行小波逆变换即可得到数据矩阵_new(×2)。

1.2 TAN降水粒子分类方法

针对修正小波变换插值后的高分辨率降水粒子雷达回波数据,本文采用TAN网络进行降水粒子分类。为了得到离散的雷达偏振参量数据集,首先对高分辨率的雷达偏振参量数据进行离散化操作,然后以降水粒子类型变量作为类别属性,偏振参量,,作为条件属性搭建TAN网络框架,接着用离散化的高分辨率雷达偏振参量数据集进行TAN网络结构和参数训练以完成TAN降水粒子分类网络的构建,最后用TAN网络实现降水粒子的分类。

1.2.1 数据离散化处理

TAN降水粒子分类方法需要数据的属性是离散化的,否则学习准确率比较低,因此本文在构建离散属性TAN网络前首先对雷达偏振参量数据做相应的离散化处理。关于数据离散化处理的各类方法中,等宽算法较为常见,本文即采用等宽区间离散化方法对雷达偏振参量数据进行离散化处理以得到所需的离散数据集。

以条件属性为例,对第21节修正小波变换插值后得到的高分辨率数据集_new进行离散化处理以得到离散数据集。

首先，生成离散化标准。假设该数据集离散化前的数据总量为,利用史特吉斯公式可以计算离散区间数:

=1+332lg

(6)

假设该数据集中最大的属性值为_max,最小的属性值为_min,根据式(7)可计算得到断点间隔:

=(_max-_min)

(7)

接着根据()=_min+(=1,2，…,)求断点,得到的断点集为=[(1),(2),…,(),…,()]，此处得到的断点集称为离散化标准。

其次,生成离散数据集。离散数据集是按最小欧式距离准则,根据上述离散化标准生成的。方法如下:依次取出高分辨率数据集_new中的各个数据,计算当前取出的数据_new()(=1,2,…,)与离散化标准(=[(1),(2),…,(),…,()])中每一个元素(∈)的欧式距离=[,1,,2,…,,],找到集合中最小欧式距离min,,(,∈),确定与min,对应的断点()(()∈),该断点即原数据经离散化后得到的数据值。将该数据放入离散数据集中,令()=(),作为离散数据集中的第个元素,直至遍历原数据集_new中的所有元素即可得到最终的离散数据集。

按照上述方法对偏振参量和做同样的处理,得到和的离散数据集为与,离散化标准为(1×)与(1×)。

122 TAN网络结构训练

对雷达偏振参量数据做离散化处理后,接下来进行TAN网络结构训练。首先需要确定TAN网络的类节点和属性节点,本文以降水粒子类型变量作为TAN网络的类节点,属性节点由偏振参量属性变量，,来充当,以此构造初始TAN网络结构。接着根据互信息理论继续确定各属性节点间的依赖关系并通过添加扩展弧的方式对初始TAN网络结构进行优化。最后得到与样本数据集匹配度最好的TAN网络结构。初始TAN网络结构图如图2所示。

图2 初始TAN网络结构图Fig.2 Initial TAN network structure diagram

图2中,圆形称为网络的节点,网络的边是图中的有向线段,边所指向的节点称为子节点,边的出发端节点是父节点,父节点的数据值会对子节点的数据取值有一定的影响。

接下来根据互信息理论对TAN网络结构继续进行优化。在图2的基础上通过计算属性节点,,两两之间的互信息并与给定互信息门限比较,从而继续确定各偏振参量属性之间的依赖关系。

以反射率因子和差分反射率为例,首先计算与之间的互信息(,)。该互信息可以通过下式得到:

(,)=

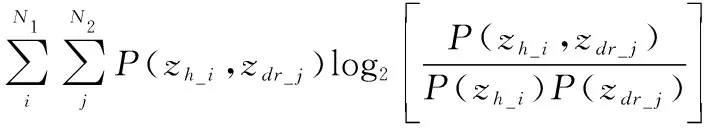
(8)

式中：,为反射率因子数据和差分反射率数据的个数;(_,_)表示偏振参量属性(,)的状态为(_,dr_)时的联合概率;(_)和(dr_)分别表示偏振参量=_时的边缘概率以及=dr_时的边缘概率,这些概率均可通过对数据样本进行统计得到。

接下来将互信息(,)与互信息门限(一般取001≤002)比较,若(,)≤,则认为偏振参量与之间不存在关联性;若(,)>,则表明偏振参量与之间存在关联性,此时要在属性节点与间新增一条边,暂不定向。接着，根据式(8)计算属性节点和与类节点之间的互信息(,)与(,),比较(,)与(,),若(,)>(,),则新增边的箭头由属性节点指向属性节点;若(,)<(,),则新增边的箭头由属性节点指向属性节点;若(,)=(,),则随机定向。最后更换属性节点,用上述同样的方法确定其他属性节点两两之间的依赖关系,并通过加带箭头边的方式体现在TAN网络结构中。TAN网络结构的具体训练过程如下。

构建初始TAN网络结构,初始TAN网络结构的属性节点为雷达偏振参量,,,类节点为降水粒子类型变量。

给定互信息门限(一般取001≤≤002)。

计算属性节点与之间的互信息并与门限比较,若(,)>则执行步骤4;若(,)≤则执行步骤5。

在属性节点对和之间建立一条无向边,然后根据属性节点和与类节点之间互信息值的大小来确定无向边的方向,由互信息值大的属性节点指向互信息值小的属性节点,若两个互信息值一样大小则属性节点间无向边的方向可随机指向任一节点。

更换属性节点并重新执行步骤3,直到两两属性节点对均遍历完为止。

以上TAN网络结构训练的操作流程图如图3所示。

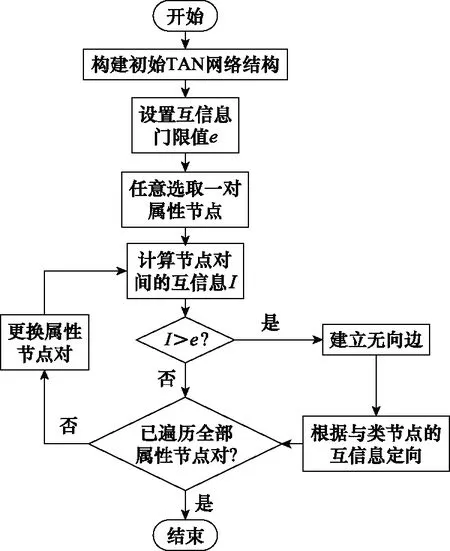
图3 TAN网络结构训练操作流程图Fig.3 Flow chart of TAN network structure training operation

为了得到最终的TAN分类网络结构图,将各离散化高分辨率雷达偏振参量数据集按照上述流程图进行TAN网络结构训练,最终得到的结构图如图4所示。

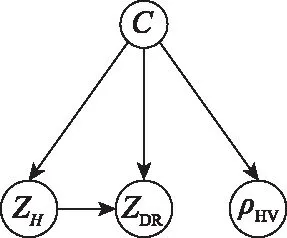
图4 TAN降水粒子分类网络结构图Fig.4 Structure diagram of TAN hydrometeor classification network

1.2.3 TAN网络参数训练

离散属性TAN网络使用条件概率表描述雷达偏振参量对不同降水粒子的分布,条件概率表为一种分布列,为了得到各个节点的条件概率表,故进行相应的TAN网络参数训练。

图4的TAN网络结构图中,属性节点的条件概率与节点和的数值都有关系,因为属性节点的父节点有两个,即和。根据第221节得到的偏振参量的离散化标准的维数,以及偏振参量的离散化标准的维数,同时结合类标签=(=1,2,…,9)(代表9种粒子类型)的维数可以确定属性节点的条件概率表为××9的三维分布列。

将第221节经过离散化处理后得到的各偏振参量的离散数据集作为训练数据集,用()表示训练数据集的样本个数,将训练数据集中满足=()(=1,2,…,),=()(=1,2,…,),=(=1,2,…,9)的样本个数记为(()∩()∩),那么条件概率表中条件概率计算方式如下:

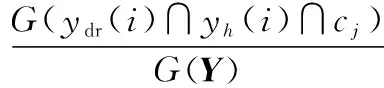
(9)

在训练数据集中可能存在(()∩()∩)=0这种情形,因为后续分类运算涉及到乘法运算,所以这种情况会对分类结果产生消极影响,故通过拉普拉斯平滑对式(9)做相应的处理,具体操作如下所示:

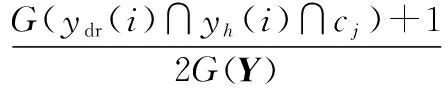
(10)

以属性节点为例,说明参数训练过程,如图5为的条件概率表示意图,其中每个单元格表示对应各雷达偏振参量取值的概率。

图5 ZDR条件概率表示意图Fig.5 ZDR conditional probability indication intention

假设训练数据集中样本个数为,满足图5中标出单元格=-0410 5,=8489 7,=的样本个数为,则该单元内概率计算方式如下所示：

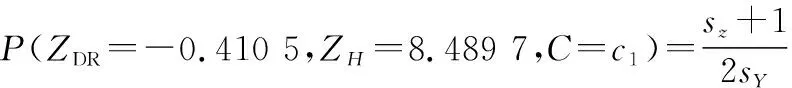
(11)

根据这种计算方式,计算出每个雷达偏振参量节点的条件概率表,可完成参数训练。

124 TAN网络的降水粒子分类原理

通过上述TAN网络结构训练和参数训练构建好TAN网络后,下面对TAN网络的具体分类原理进行论述。

用(=1,2,…,9)表示类节点的各种可能取值,即各类降水粒子类型,其中表示地杂波(将地杂波也看作一种降水粒子)、表示冰晶、表示干雪、表示湿雪、表示雨、表示暴雨、表示大雨滴、表示霰、表示雨夹雹。根据贝叶斯分类算法的基本原理,若以上TAN网络中3种偏振参量,,的取值分别为,,,则分类结果为的概率(|,,)可表示为

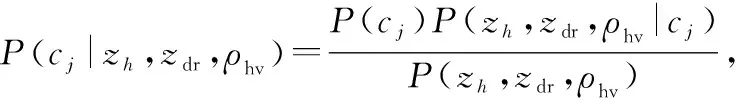
(12)

式中：()代表的是第类降水粒子的先验概率,在未知的情况下一般采用等概率,即()=1(=1,2,…,9);(,,)表示偏振参量取值为,,的数据出现的概率,在样本确定的情况下该概率值是固定的;(,,|)称为类条件概率,根据训练得到的TAN网络结构,该概率值可计算如下:

(,,|)=(|)(|,)(|)，=1,2,…,9

(13)

式中：(|)表示在约束条件为时取值为的数据出现的概率;(|,)与(|)同理。此处的概率值通过对TAN网络进行参数训练记录在条件概率表中。

最终的分类结果可以计算如下:

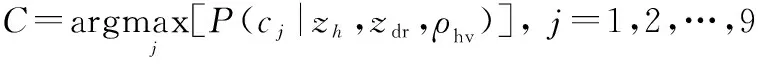
(14)

式(14)所表达的含义是:计算偏振参量值,,对应每种分类结果(=1,2,…,9)的概率(|,,),取其中概率值最大的作为分类结果输出。

2 算法流程与步骤

本文中双偏振天气雷达体制下的修正小波变换插值-TAN的降水分类方法详细操作步骤如下。

基于修正小波变换插值方法对低分辨率雷达偏振参量数据进行插值处理以获得高分辨率雷达偏振参量数据。

在步骤1得到的对高分辨率数据的基础上实行等距离散化操作,最终得到所需的离散数据集。

构造初始TAN网络结构,初始TAN网络结构的属性节点由各偏振参量变量充当,类节点由降水粒子类别变量充当。

引入互信息理论,使用离散化雷达偏振参量数据对初始TAN网络结构重新进行结构训练,接着进行参数训练,获得最终的TAN网络。

使用最终的TAN网络对离散的高分辨率雷达偏振参量数据进行降水粒子分类。

综上所述,双偏振天气雷达体制下修正小波变换插值-TAN的降水粒子分类方法整体流程图如图6所示。

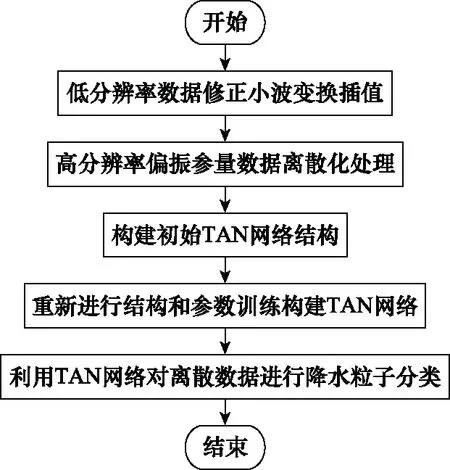
图6 基于修正小波变换插值-TAN的降水粒子分类方法流程图Fig.6 Flow chart of hydrometeor classification method based on modified wavelet transform interpolation-TAN

3 实验结果及分析

为了验证所提方法的性能,本文选取美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)数据库中的KTLX雷达提供的偏振参量数据进行实验。KTLX雷达为美国WSR-88D雷达网中位于俄克拉荷马市(35.195 8 N°, 97.164 0 W°)的一部双偏振气象雷达。这部雷达的波束宽度是1.25°,天线增益是45 dB,脉冲重复频率是250～1 200 Hz,带宽是0.3 MHz,该雷达的回波分辨率为360×300。首先基于修正小波变换法对获得的回波数据做两次插值的操作,接下来再做降水粒子分类,将得到的降水粒子分类结果与美国国家海洋和大气管理局官网提供的高分辨率数据(360×1 200)的分类结果进行对比,计算分类误差。为了说明所提方法的可靠性,此处选取两组数据进行实验。

根据图7和图8,TAN方法对插值后数据的分类结果接近于NOAA提供的标准数据分类结果,在此基础上对分类结果误差进行了统计,经统计分类误差均处于较低水平,2017年为1.37%,2018年为0.92%。根据上述实验分析可以看出，本文方法在数据量仅为标准数据25%的条件下能够实现准确的数据插值处理结果以及降水粒子分类。

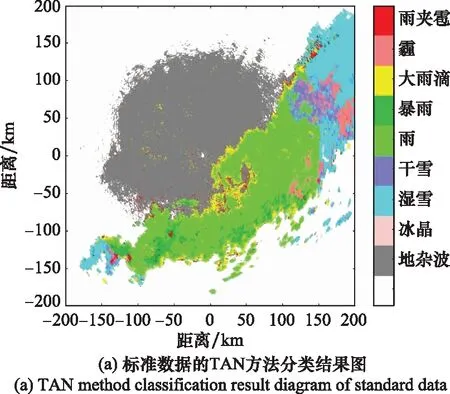
图7 2017年8月17日标准数据与插值重构后数据的 TAN降水粒子分类结果对比图Fig.7 Comparison diagram of precipitation particle classification results between standard data and interpolated reconstructed data on August 17, 2017

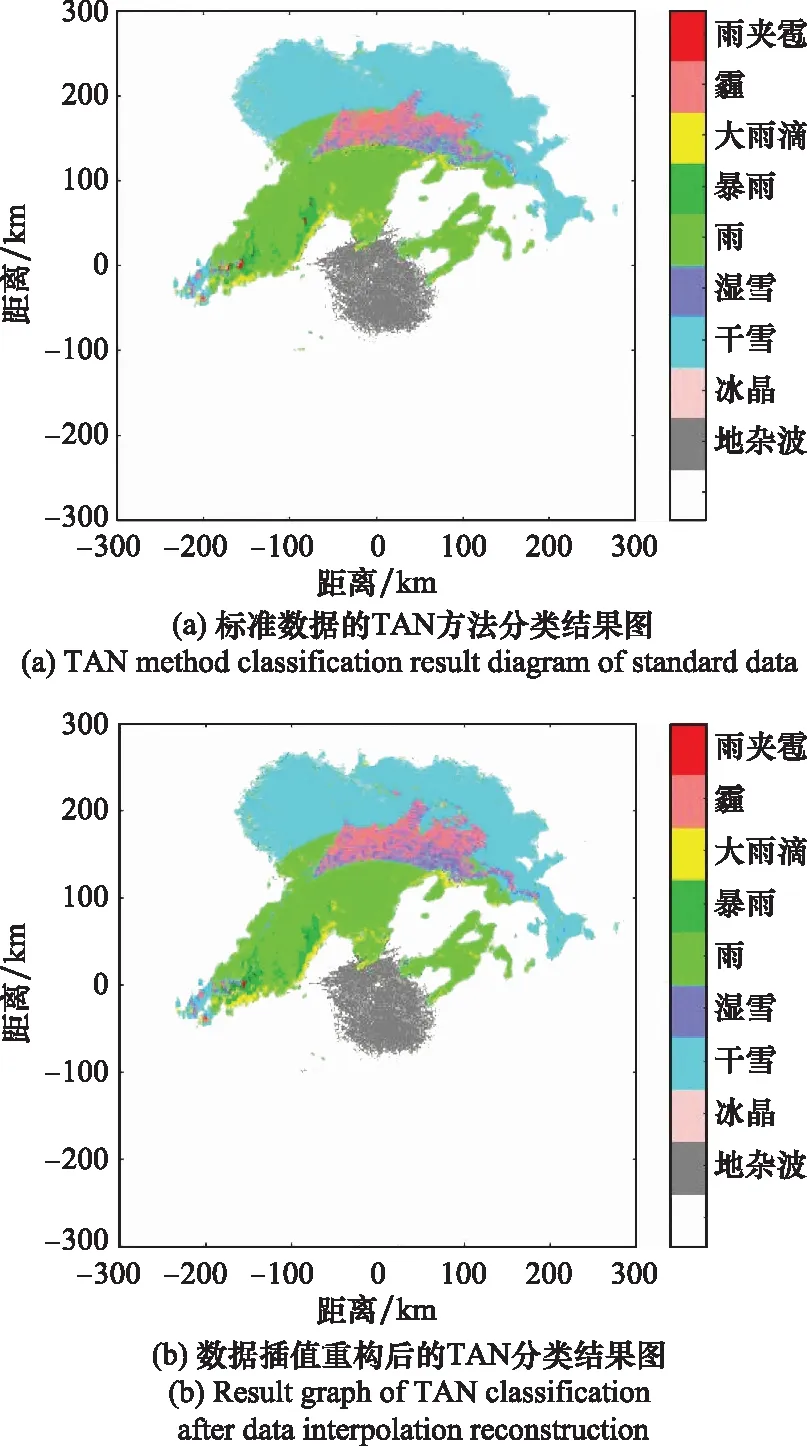
图8 2018年6月24日标准数据与插值重构后数据的 TAN降水粒子分类结果对比图Fig.8 Comparison diagram of precipitation particle classification results between standard data and interpolated reconstructed data on June 24, 2018

为了进一步说明TAN降水粒子分类方法的有效性,仍以上述两组数据为样本进行降水粒子的分类研究,图9和图10分别给出了使用模糊逻辑算法和TAN算法得到的降水粒子分类结果以及NOAA给出的降水粒子分类结果。

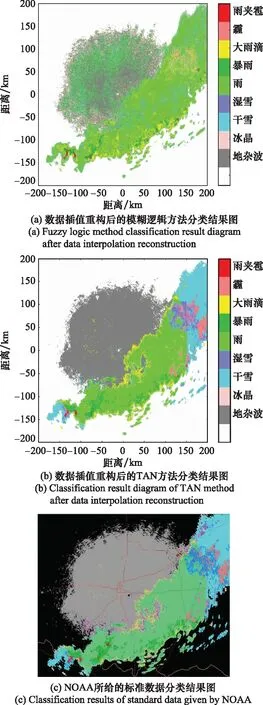
图9 2017年8月17日数据的不同降水粒子分类方法结果对比图Fig.9 Comparison diagram of the results of different precipitation particle classification methods based on the data on August 17, 2017

分析图9与图10,对在不同时间段获取的雷达偏振参量数据进行降水粒子分类,模糊逻辑法的分类结果均存在一定误差。图9(a)中,除了没有准确识别地杂波外,对其他降水粒子也没有做到准确分类,将很多非雨的降水类型误识别为雨。而图10(a)中,模糊逻辑方法对湿雪和霰完全未能识别出来。而本文所提的TAN降水粒子分类方法针对不同时间段获得的数据分类效果均较好,与NOAA提供的结果更为相近。综上可知,对不同时间段的降水粒子进行分类,TAN方法的分类效果均比较稳定,不会产生较大误差。

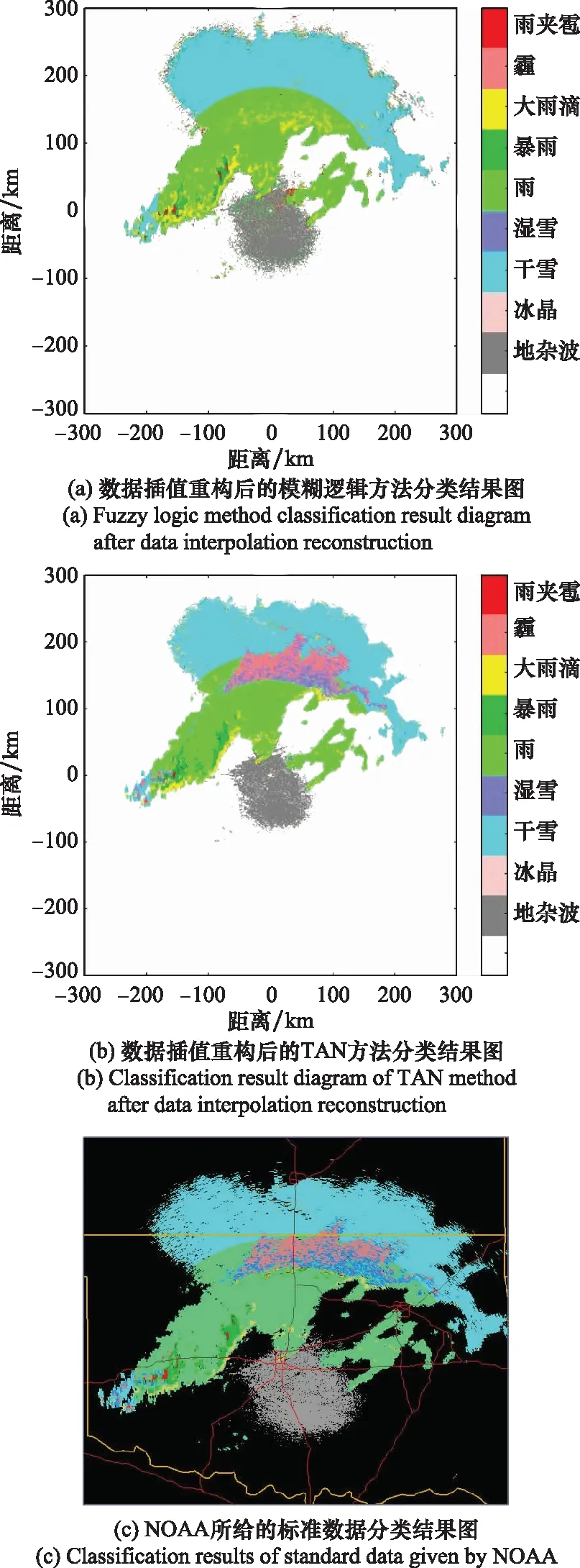
图10 2018年6月24日数据的不同降水粒子分类方法结果对比图Fig.10 Comparison diagram of the results of different precipitation particle classification methods based on the data on June 24, 2018

4 结 论

对于双偏振雷达体制下数据分辨率较低时的降水粒子分类问题,本文给出了基于修正小波变换插值-TAN的雷达降水粒子分类方法。该方法首先对原始低分辨率雷达偏振参量数据进行修正小波变换插值以得到插值后高分辨率雷达偏振参量数据。接着，把雷达偏振参量变量当作属性节点,把表示降水粒子类型的变量作为类节点去构造初始TAN网络结构,并在此基础上引入互信息理论,利用离散化的高分辨率偏振参量数据重新进行TAN网络结构和参数训练以完成最优TAN网络的构建。最后,将插值后高分辨率偏振参量数据带入到训练好的TAN网络中实现降水粒子的分类。该方法在数据插值处理中可以更多地保留原始数据的高频信息,另外通过数据样本训练方式计算TAN网络分类参数的方法比以经验值作为分类参数的传统模糊逻辑方法的分类稳定性更好。上述实验结果表明,该方法可以获得较为准确的数据插值与降水粒子分类结果。