多种转发干扰下的脉内脉间波形综合优化设计

2022-05-07叶春茂李璋峰鲁耀兵

系统工程与电子技术 2022年5期

张彦, 叶春茂, 李璋峰, 鲁耀兵

(北京无线电测量研究所, 北京 100854)

0 引言

在复杂电磁对抗场景中,雷达目标探测可受多种并存的有源干扰影响,严重降低了雷达的探测效果。随着数字射频存储(digital radio frequency memory, DRFM)技术的发展,干扰机可以截获、调制、转发雷达信号,从而产生相干性高的多种转发干扰,根据干扰机采样转发方式可分为间歇采样转发干扰(interrupted sampling repeater jamming, ISRJ)与全脉冲采样转发干扰(full-pulse sampling repeater jamming, FSRJ)。

ISRJ交替地存储与调制转发截获的雷达信号,具有较小的时延和较强的相干性,可以在一个脉冲内形成多个假目标,兼具压制和欺骗效果。具体样式包括直接转发干扰、重复转发干扰、非均匀转发干扰以及其他间歇采样调制转发干扰。FSRJ是将截获到的整个脉冲信号进行存储,再进行调制转发,常常延迟一个或多个脉冲重复周期,可以在真实目标附近形成逼真假目标。具体样式包括距离速度拖引干扰、密集重复转发干扰、模板调制转发干扰以及其他全脉冲采样调制转发干扰。目前,针对ISRJ的干扰对抗方法主要有能量函数幅值抑制方法、时频分析滤波器设计方法以及频率相位编码波形设计方法。而针对FSRJ的对抗方法主要有正交分集波形设计、编码波形相参积累以及频率捷变波形联合信号分析的方法。

上述干扰对抗方法,多针对一种特定的干扰样式,在多种干扰样式并存时效果下降。因此,在多种转发干扰样式下展开脉内脉间波形综合优化设计很有必要。现阶段,脉内脉间波形综合优化设计已发展出一套完整的流程,可通过对编码波形的参数优化提高目标检测概率、降低成像副瓣以及提高跟踪精度。本文在分析多种转发式干扰样式的基础上,设计出独特的代价函数,利用遗传算法(genetic algorithm, GA)与模拟退火(simulated annealing, SA)算法综合优化波形参数,仿真验证所设计的波形具有良好的干扰抑制效果。

1 多种转发干扰模型

1.1 脉内转发干扰

ISRJ可以形成脉内转发干扰,典型干扰样式即间歇采样直接转发与间歇采样重复转发,如图1所示。

图1 脉内转发干扰示意图Fig.1 Schematic diagram of intra pulse repeater jamming

ISRJ直接转发干扰对采样到的一小段信号直接转发,随后再采样一小段信号,可表示为

()=(-)·(-)

(1)

式中:()为干扰机转发信号;()为雷达信号;()为干扰机采样过程;为干扰机采样脉冲宽度。ISRJ重复转发干扰对采样到的一小段信号,按设定次数重复转发,随后再采样一小段信号重复转发,可表示为

(2)

式中:为设定的重复转发次数。ISRJ的采样过程()可表示为矩形脉冲串,表达式为

(3)

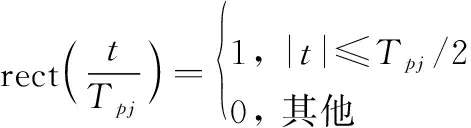
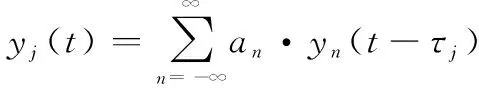
(4)

式中:加权系数=sinc(π·)与干扰机采样占空比有关;()为ISRJ脉压输出的阶谐波分量,可表示为

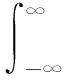
(5)

式中:()为雷达信号()的频谱;=1为ISRJ间歇频率。故ISRJ脉压结果为雷达信号不同频移调制为±的加权叠加和。具体分析,当发射线性调频脉冲串时,ISRJ直接转发干扰产生规律假目标群,假目标在延迟处对称分布,假目标幅值由对称中心向两边快速衰减;ISRJ重复转发干扰产生多个假目标群,围绕对称中心分布,假目标幅值同样由对称中心向两边快速衰减,兼具压制与欺骗效果。

1.2 脉间转发干扰

FSRJ则形成脉间转发干扰,典型干扰样式即全脉冲采样直接转发干扰与全脉冲采样密集转发干扰如图2所示。

图2 脉间转发干扰示意图Fig.2 Schematic diagram of inter pulse repeater jamming

全脉冲采样直接转发干扰对雷达发射的整个脉冲进行采样,经过延迟与幅值调制后转发,可表示为

(6)

式中:为脉冲串个数;()为干扰机截获的雷达信号;()为不同脉冲的延迟调制量。全脉冲采样密集转发干扰则对采样到的整个脉冲,延迟多个不同的分量调制后转发,可表示为

(7)

式中:为密集转发次数;(,)为第个脉冲、第次转发的延迟量。延迟多个分量可通过卷积冲击函数串的形式实现,可表示为

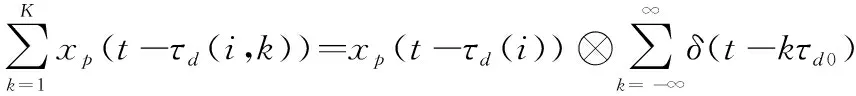
(8)

式中:0为重复转发间隔时间。则全脉冲采样密集转发干扰的脉压结果为

()=()⊗()=

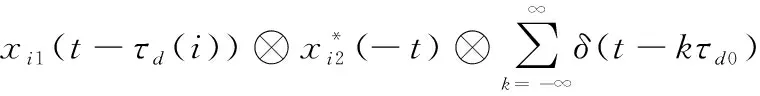
(9)

式中:1()为干扰机截获的1时刻雷达脉冲;2()为雷达当前2时刻所对应的脉冲;()为当前2时刻的匹配滤波器。故全脉冲采样密集转发干扰脉压结果与脉冲间的相关性有关。当发射线性调频脉冲串时,不同脉冲间的相关性高,可产生间隔为0的假目标群,兼具压制与欺骗效果。

2 波形优化设计方法

2.1 目标函数

经过上述分析,可知脉内脉间转发干扰的假目标产生原理不同,故在设计干扰对抗波形时需要采用不同的目标函数。ISRJ脉压结果可以等效为不同频移调制目标的加权叠加和,在脉内形成干扰与脉间调制方式无关,则目标函数为使得频移调制为±目标脉内压缩处理后的幅值最小,可表示为

min=

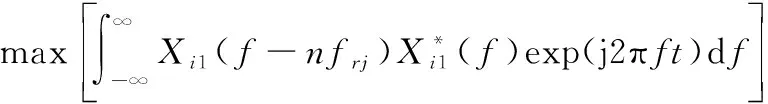
(10)

全脉冲转发干扰的脉压结果为不同脉冲间的匹配滤波输出,与脉内调制方式无关,则目标函数为使得不同脉冲间匹配滤波输出峰值最小,即相互正交,可表示为

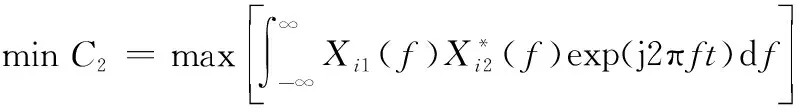
(11)

另外,设计波形时还需考虑波形本身的相关特性,即要求自相关旁瓣峰值低,可表示为

min=max(:peak1-1,peak1+1:)

(12)

式中:为自相关结果峰值;为旁瓣区间起始点幅值;为旁瓣区间终止点幅值;1为半主瓣宽度点数。故最终得到的目标函数可表示为

min()=()+()+()

(13)

式中:、、为不同目标的加权系数。所设计的波形需要保证一定的多普勒容限,则脉内采用线性调频相位编码波形;同时为防止干扰机截获跳频规律,对不同跳频脉冲采用不同的编码方式,进一步提高脉间波形的正交性。故采用脉内线性调频相位编码脉间频率捷变波形进行综合优化。

2.2 优化方法

在决定了脉内脉间波形调制方式,获得了波形优化的目标函数之后,需要通过优化方法对波形参数进行优化。常用的智能优化算法,如GA与SA算法对参数选择较为苛刻,不合适的参数对于优化效果影响较大,因此采用GA与SA算法的混合优化策略(简称为GASA),提高算法的优化性能与鲁棒性,算法流程图如图3所示。

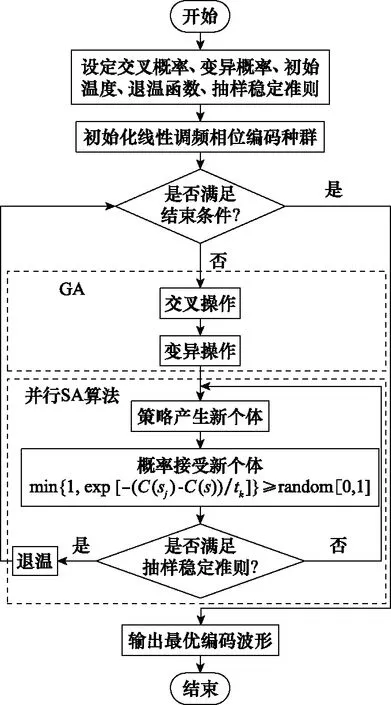
图3 GASA算法流程图Fig.3 Flow chart of GASA algorithm

优化算法初始化环节,初始化种群数量并对所设计波形的各个参数,如信号脉宽、带宽、相位编码种类、编码长度、跳频区间进行设定,同时设定GA的交叉概率与变异概率,设定SA算法的初始温度、退温函数+1=()与抽样稳定准则,退温函数可设定为

(14)

搜索环节,依次进入GA模块与并行SA算法模块,GA模块通过交叉与变异操作,经过自然选择产生新种群;并行SA算法模块,将产生的新种群中的所有个体并行操作,产生新状态并概率接受新个体,接受新个体的准则为

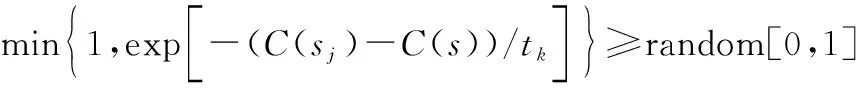
(15)

式中:random[0,1]表示在[0,1]间取随机数;表示新个体;表示实时温度。当满足抽样稳定准则后退温,并判决是否满足波形参数搜索结束条件,不满足则循环搜索,满足则输出多个脉冲的脉内线性调频相位编码与脉间跳频编码的参数矩阵。

3 仿真实验

为验证所设计波形对干扰抑制的有效性,将3种波形在多种转发干扰下的效果进行比较。波形1:脉内线性调频,脉间恒频脉冲串波形,即传统的线性调频脉冲串波形;波形2:脉内线性调频相位编码,脉间跳频随机波形,随机编码不经过优化设计;波形3:脉内线性调频相位编码,脉间跳频优化波形,编码方式经过目标函数优化设计。

设置雷达参数,脉内线性调频相位编码信号的带宽为100 MHz,脉宽为100 μs,脉冲重复间隔为1 ms,编码长度为600段,采用四相编码的方式进行,脉间跳频编码信号的跳频区间为9～11 GHz;目标为散射点模型,相位位置为0 m与3 m,散射点回波幅值均为1;ISRJ采用收1发2的重复转发的干扰模式,间歇采样时长为2 μs,间歇转发周期为6 μs,干扰增益为20 dB,全脉冲采样密集转发干扰,密集转发间隔0为04 μs,干扰增益为30 dB;脉压后信噪比SNR为20 dB。

仿真脉冲数为100,其中脉冲1～10无干扰,脉冲11～40仅含有脉内ISRJ重复转发干扰,脉冲41～70仅含有全采样密集转发干扰,脉冲71～100则同时存在上述两种转发干扰。得到3种波形下的自相关与互相关结果如图4所示,脉内ISRJ重复转发干扰的脉压结果如图5所示,脉间全脉冲采样密集转发干扰的脉压结果如图6所示,脉内脉间多种转发干扰的脉压结果如图7所示,整个脉冲的脉压结果序列如图8所示。

图4 波形自相关与互相关结果Fig.4 Results of auto correlation and cross correlation

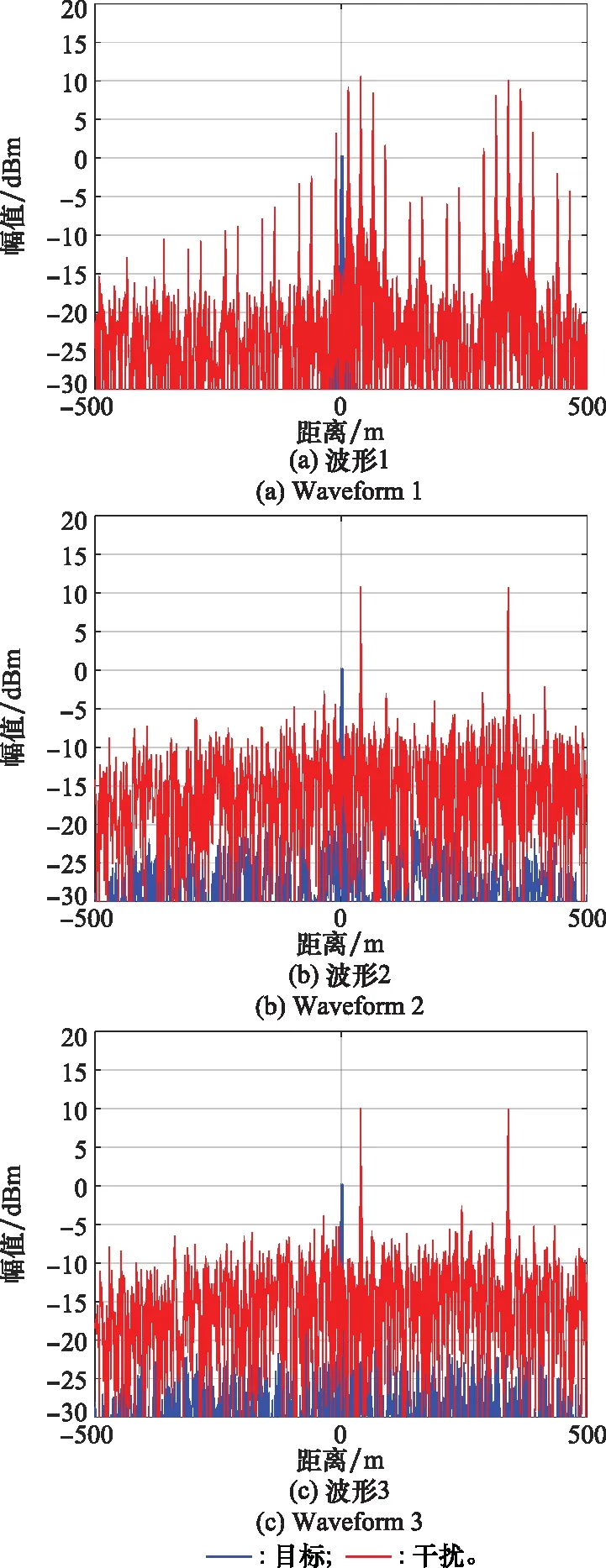
图5 脉内间歇采样重复转发干扰脉压结果Fig.5 Pulse compression results of intra pulse interrupted sampling repetitive repeater jamming

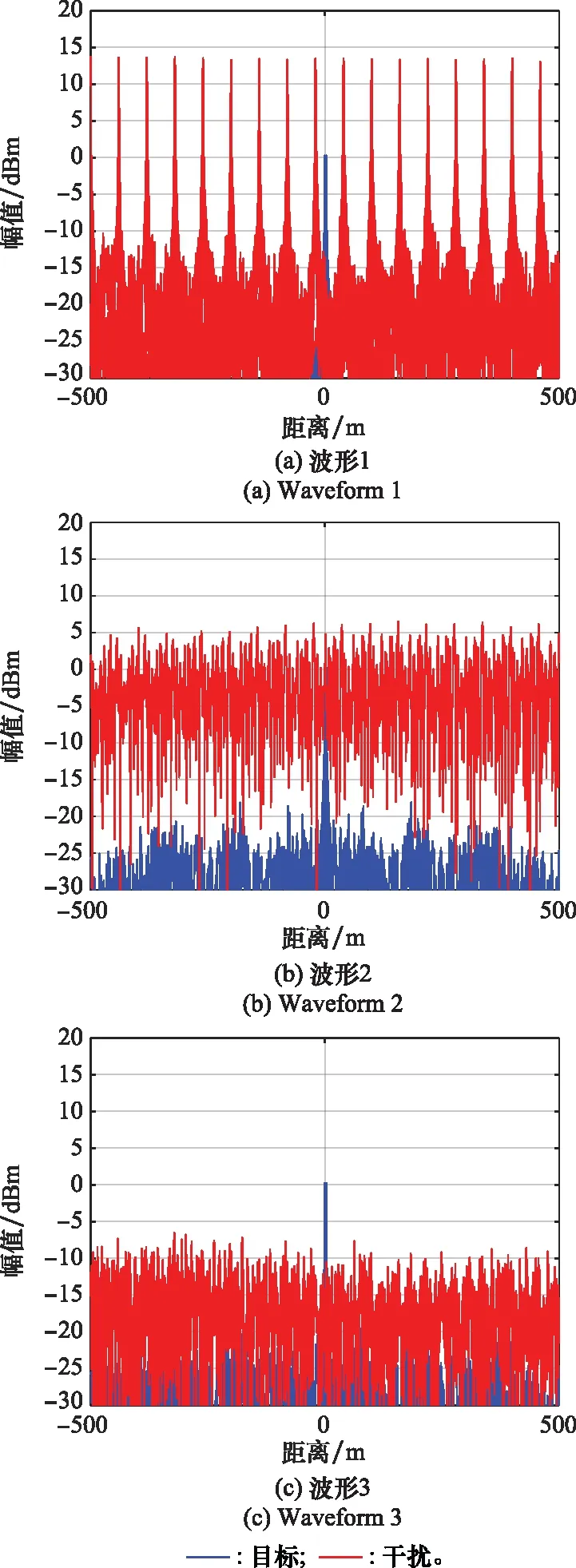
图6 脉间全脉冲采样密集转发干扰脉压结果Fig.6 Pulse compression results of inter pulse full pulse sampling dense repeater jamming

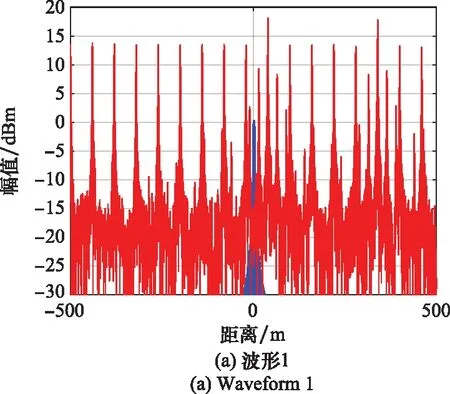
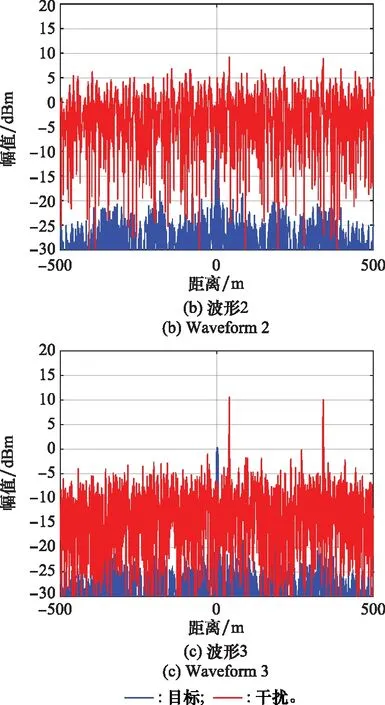
图7 脉内脉间多种转发干扰脉压结果Fig.7 Pulse compression results of multiple intra and inter pulse repeater jamming

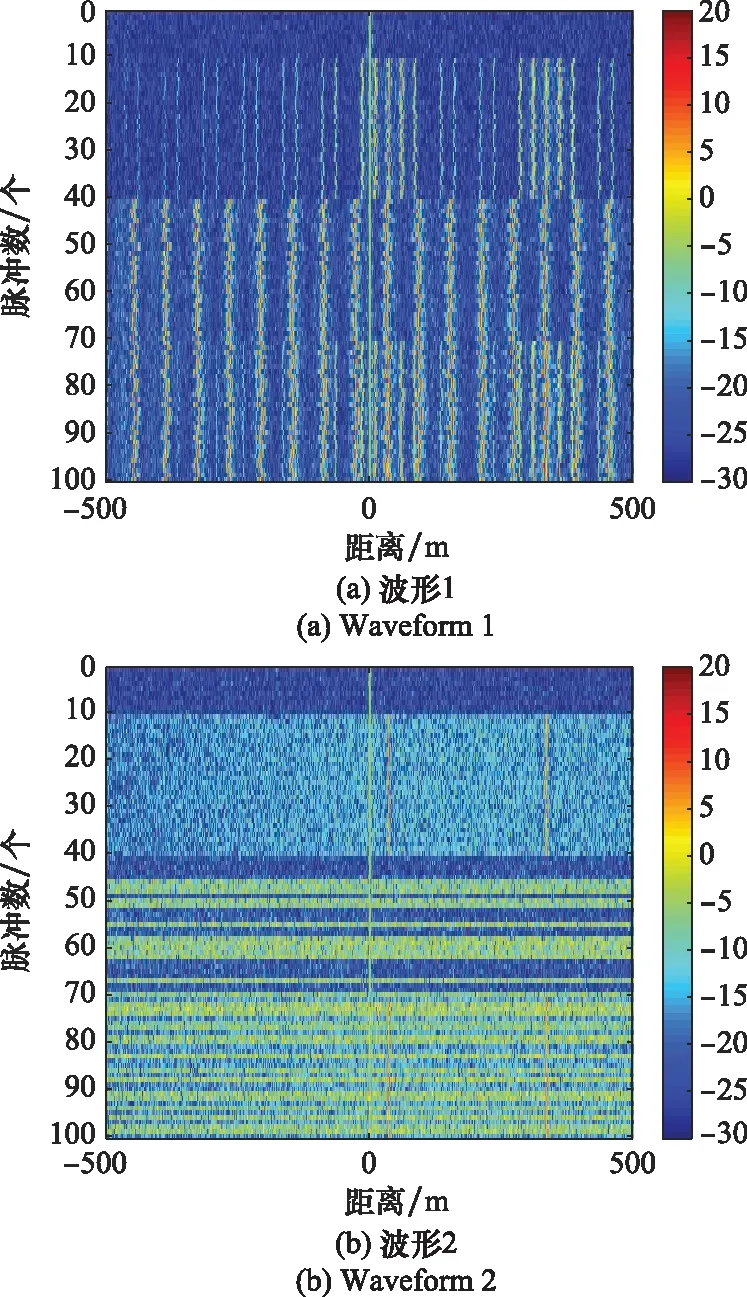
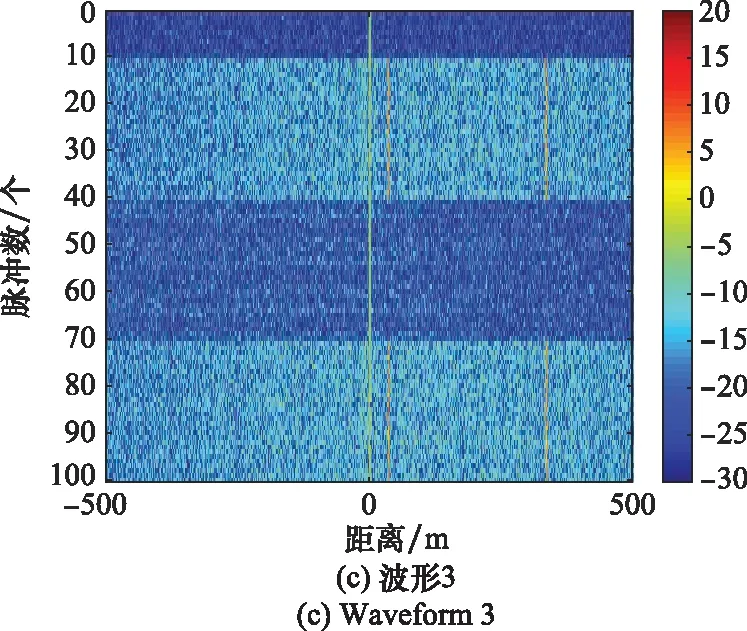
图8 脉压结果序列图Fig.8 Sequence diagram of pulse compression results

图4中,蓝色实线为波形同一脉冲自相关结果,红色实线为波形不同脉冲间的互相关结果,可以看出波形3的脉间正交性最好,即脉间转发干扰在所设计的波形下获得的脉压增益最小。图5～图7中,蓝色实线均为目标脉压结果,红色实线为不同干扰脉压结果。比较图5可以看出,对ISRJ波形3具有良好的抑制效果,次假目标幅值下降明显,波形2具有一定的抑制效果,次假目标幅值有所下降,而波形1形成了规律分布的假目标。比较图6可以看出,对全脉冲采样密集转发干扰,波形3抑制效果明显,梳状假目标幅值下降接近噪声,波形2具有一定的抑制效果,但干扰仍有效覆盖了目标,波形1形成了梳状干扰效果。比较图7可以看出,对脉内脉间多转发干扰,波形3抑制效果明显,仅残留脉内转发干扰的主假目标,波形2的抑制效果有限,干扰幅值下降但覆盖了真实目标,没有达到抑制的目的,波形1的梳状干扰假目标与规律分布假目标群均存在,难以分辨真实目标。比较图8可以看出,所设计优化的波形3相对于其他两种波形,特别在多转发干扰段,目标更加突出,具有更好的干扰抑制效果。上述比较综合验证了目标函数优化后的波形3在脉内脉间多种转发干扰下的优势。

为了更好地比较波形间的干扰抑制效果,将脉压后的信干噪比(signal to jamming and noise ratio, SJNR)设定为干扰抑制效果的评价标准,可表示为

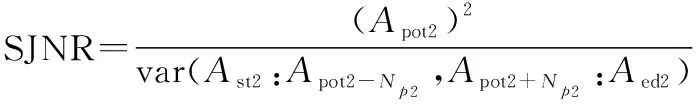
(16)

式中:为目标所在点幅值;为脉压结果起始点幅值;为脉压结果终止点幅值;2为目标附近保护点数。脉压后SJNR越大,则波形的干扰抑制效果越好。

改变波形3的目标函数,将只考虑脉内转发干扰(=0)设为波形4,与只考虑脉间转发干扰(=0)设为波形5的优化结果也进行比较,最终得到不同波形在不同转发干扰环境下的SJNR结果如表1所示。可以看出,波形3在脉内脉间多种转发干扰情况下SJNR最高,在脉内间歇采样重复转发干扰时略低于波形4但高于其他波形,在脉间全采样密集转发干扰时,略低于波形5但高于其他波形,进一步体现了所设计波形3在脉内脉间多种转发干扰下的独特优势。