利用k近邻区间距离的异步抗差航迹关联算法

衣 晓, 曾 睿,2,*, 曹昕莹

(1. 海军航空大学航空作战勤务学院, 山东 烟台 264001; 2. 中国人民解放军92325部队, 山西 大同 037001)

0 引 言

在分布式多目标跟踪融合系统中,一个重要问题是如何判断来自于不同局部节点的航迹是否源自同一目标,即航迹关联问题。然而传感器系统误差的存在增大了航迹关联的难度,使得系统误差下的航迹关联问题与误差配准问题互为前提。

为克服系统误差的影响,文献[8]通过牛顿算法优化标准函数,提出一种最小二乘配准算法;文献[9]根据同源航迹距离向量相似特征,提出基于最小平均距离的粗关联和基于分布的精关联算法;文献[10]通过推导等价量测方程,基于距离分级聚类实现航迹关联,在目标密集等复杂环境下能保持很低的错误关联率,稳定性较强。以图像匹配原理为基础,将系统误差的影响转化为旋转量和平移量,利用Fourier变换或Radon变换,文献[17]和文献[18]提出了一种不依赖于准确误差配准的航迹关联技术。文献[19]利用模糊综合决策思想,建立模糊因素集,依据航迹紧密度建立矩阵得到有效航迹关联对来实现系统误差下的航迹关联。文献[21]以目标的拓扑统计距离信息为基础,进行全局最优关联,根据双门限准则完成关联判决。上述算法的前提均是航迹同步,若航迹异步则需要时域配准,将异步航迹转换为同步航迹进行处理,但时域配准会导致航迹数据的误差传播积累,影响航迹关联算法的性能。

针对系统误差难以描述的问题,提出两种系统误差区间化方法,把带有系统误差的航迹数据转换成区间数进行处理。给出区间序列到区间点的近邻区间距离计算规则,通过不等长航迹区间序列间的相似度,实现了航迹异步和系统误差下的同时关联。本文算法可有效降低系统误差对关联结果的影响,并且无需时域配准,可对异步不等速率航迹直接关联。

1 区间序列的相似度度量

区间坐标序列与区间坐标点的近邻区间距离

设非空区间坐标序列为

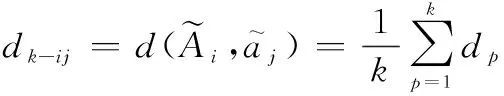
(1)

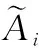
不等长区间坐标序列间的相似度

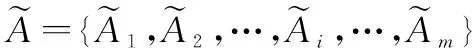
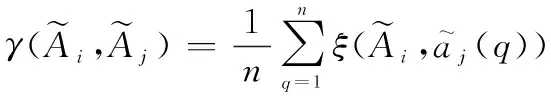
(2)

式中:

(3)

定义1、定义2中坐标变量均为三维坐标,适用于三维空间;对于二维情况,只需相应变更坐标变量维数即可。

2 利用k近邻区间距离的航迹关联算法

2.1 问题描述

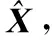
单侧区间化:假设局部节点传感器的系统误差偏差方向已知,即Δ∈(0,Δ),Δ∈(0,Δ),则在不考虑量测随机误差的条件下,观测值与真值满足:

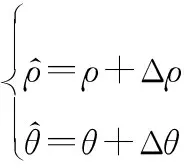
(4)

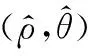
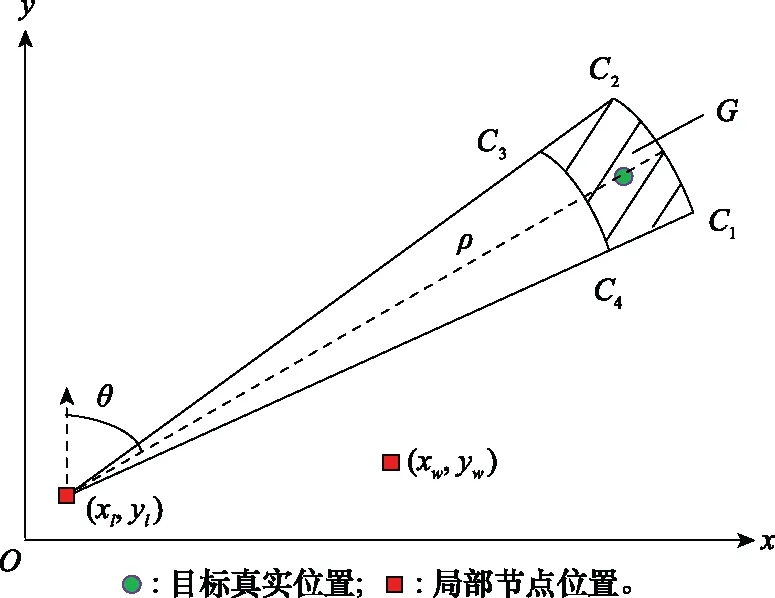
图1 系统误差双侧区间化示意图Fig.1 Diagram of bilateral interval of system bias

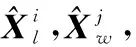
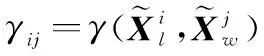
(5)

越大说明航迹和航迹越有可能对应同一目标,根据区间相似度,可利用多维分配法进行航迹关联判定。

2.2 航迹序列相似度的计算

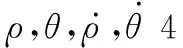
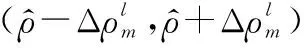
(6)

式中:

=[,,,]=[,,,]

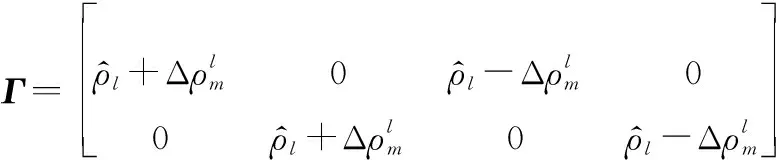
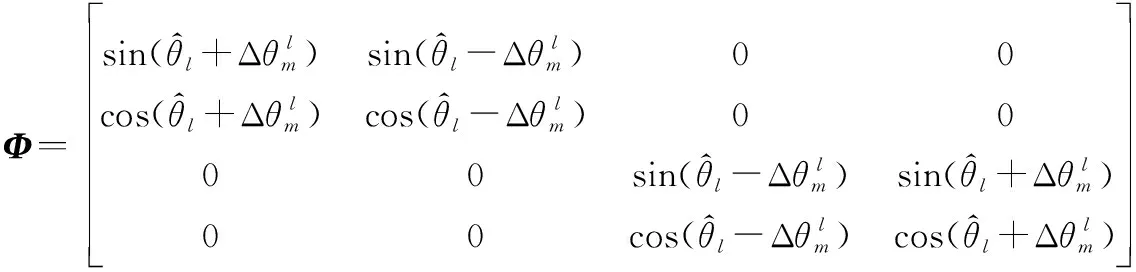
将系统误差区间化处理后的区间坐标记为

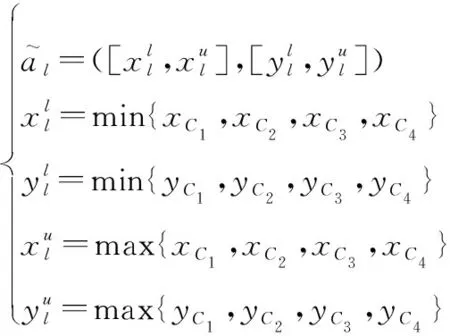
(7)

利用式(7),可将局部节点的第条航迹区间序列记为

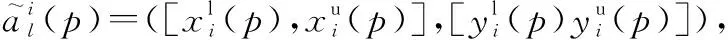
同理,可将局部节点的第条航迹区间坐标序列记为

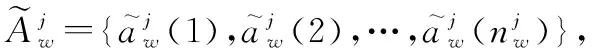
航迹区间坐标序列关联列向量可表示为

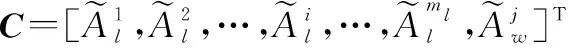
(8)

航迹区间坐标序列关联列向量的维数为+1,每行表示各航迹区间坐标序列,由于各航迹长度不同,每行元素集合的长度也有差异。其中前行表示来自局部节点的比较航迹,第+1行表示来自局部节点的参考航迹。

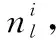
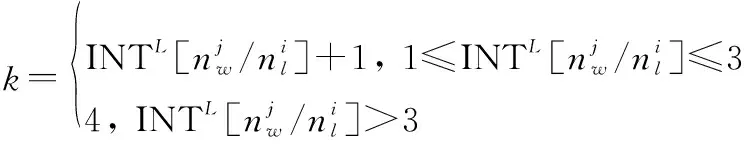
(9)

式中:INT[]表示不小于的最小整数。

根据定义1中对区间坐标序列与区间坐标点间距离的定义,计算比较序列与参考序列间的近邻区间距离矩阵为

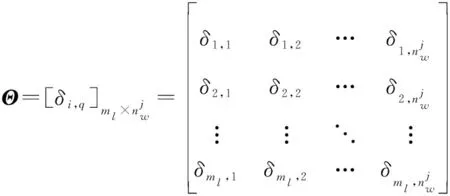
(10)

式中:

(11)

进一步利用定义2可以求得局部节点的第条航迹区间序列与局部节点的第条航迹区间序列的灰色关联度为

(12)

式中:

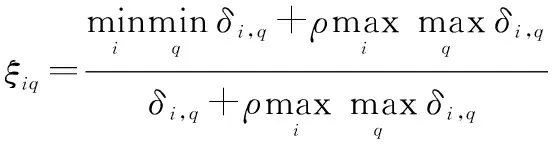
(13)

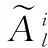
2.3 航迹关联判决

对局部节点,上报的,条航迹一一计算灰色关联度,组成×维灰色关联度矩阵,利用经典分配法进行航迹关联判决。

令变量

(14)

将目标函数记为

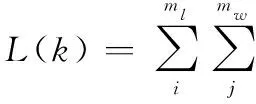
(15)

构成以下二维分配问题:

(16)

图2给出了利用近邻区间距离的异步抗差航迹关联算法的流程图。

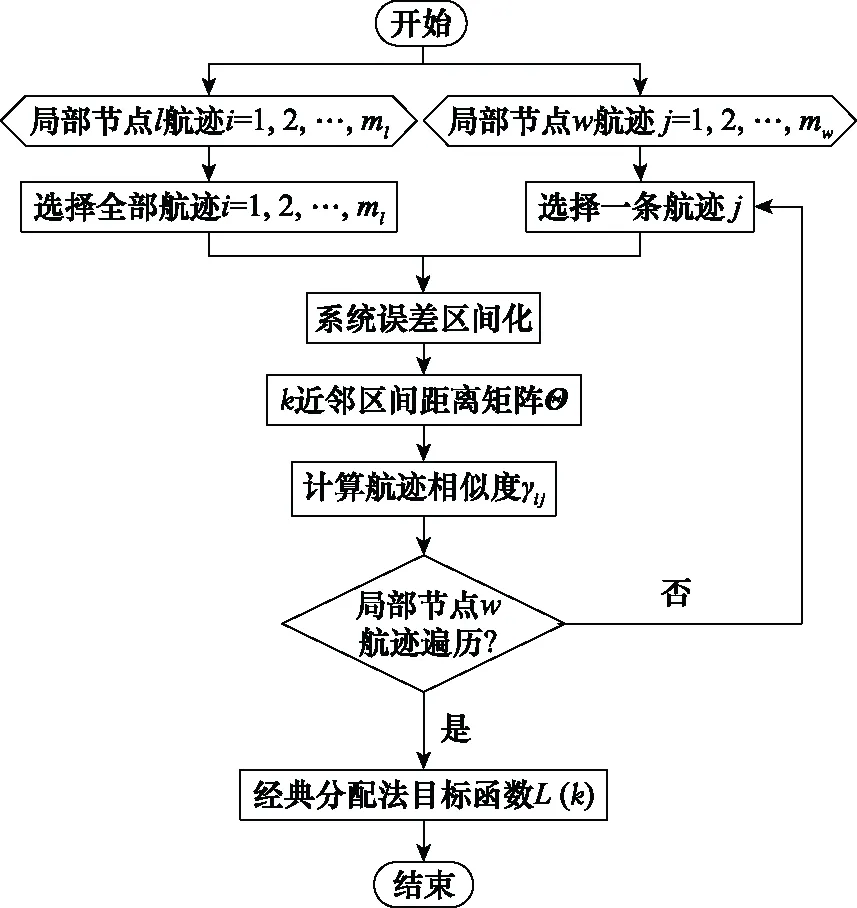
图2 算法流程图Fig.2 Flowchart of algorithm

3 仿真验证与分析

3.1 仿真环境

假设多目标跟踪系统由2个异地配置的局部节点构成,对20批目标实施不间断跟踪观测35 s。局部节点1位置坐标为(0,0),局部节点2位置坐标为(100 km,0 km),局部节点1,2的传感器采样周期均为0.2 s。

假设机动目标在二维平面中一直处于匀速直线运动状态,目标初始航向区间为[0,2πrad],初始航速区间为[200 m/s, 400 m/s]。局部节点1和局部节点2的传感器测距和测角的随机测量误差均为=50 m、=0.02 rad。进行100次蒙特卡罗仿真实验。

3.2 k的取值分析

对取值做出简要理论分析:如若取值为1,相当于未对异步航迹情况做出处理,且易受个例影响导致关联结果波动较大;若的取值等于局部节点的航迹点数目,意味着所有航迹点都将参与距离的计算,最终关联效果将显著降低。

图3给出了不同取值时的耗时对比。可以看出,随着取值增大,耗时也逐渐加大。这是因为的取值越大意味着要纳入计算点迹距离的航迹区间点越多,因此耗时也越高。

图3 不同k取值的耗时对比Fig.3 Time comparison of different values on k

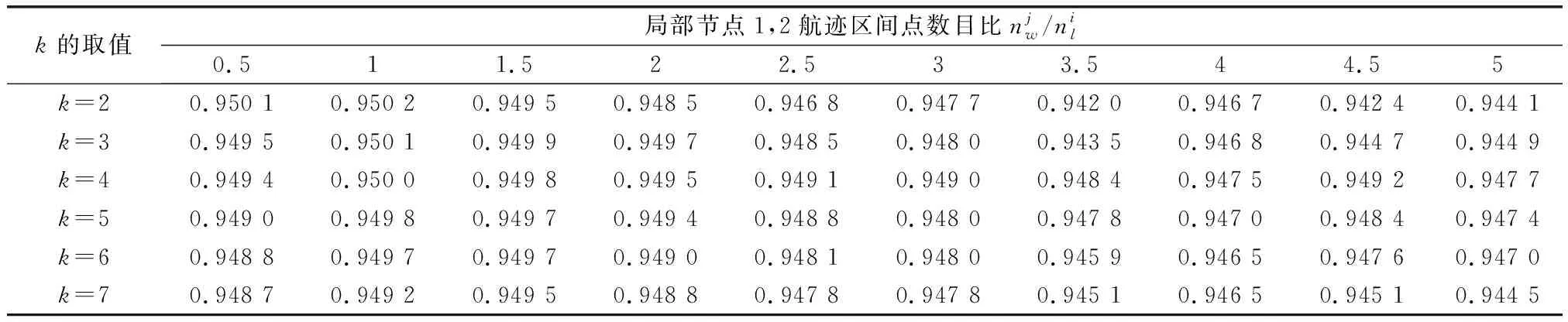
表1 不同k取值和局部节点1,2航迹区间点数目比的正确关联率

3.3 区间化方式比较与分析

在仿真环境中,固定两个局部节点传感器最大测角系统误差分别为05°和1°,假设单侧区间化的测距系统误差满足Δ∈(0,Δ),改变两个局部节点传感器的最大测距系统误差,对两种区间化方式进行比较。

图4给出不同区间化方式关联结果的比较。对观测数据的区间化处理会增加不确定度,相较于单侧区间化,双侧区间化处理后数据的不确定度更大。但从图中可知,在两个局部节点传感器最大测距系统误差不同时,两种区间化方式的关联效果相当。由于双侧区间化对最大系统误差的先验信息要求低,故整体性能优于单侧区间化。若在实际应用中采用双侧区间化处理,则只需知道最大系统误差即可进行准确关联。

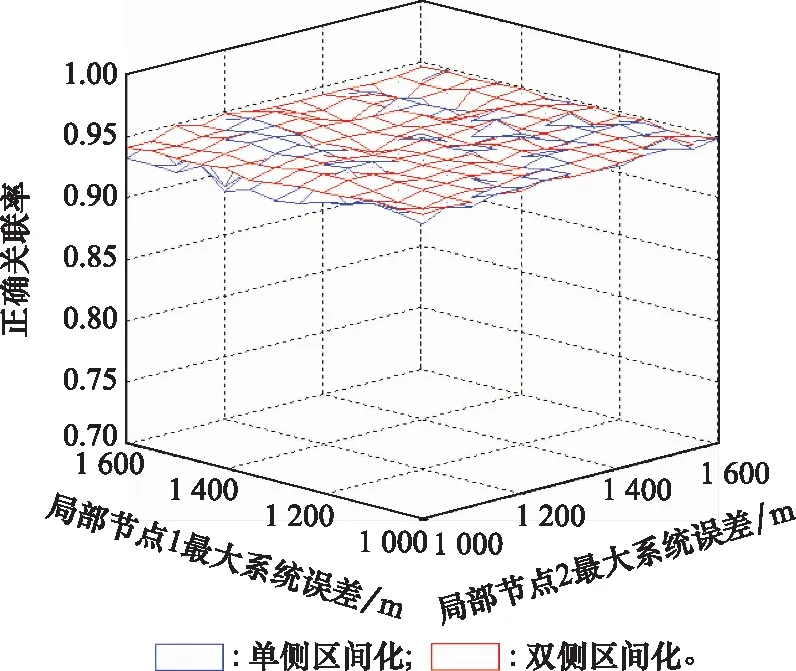
图4 区间化方式关联结果比较Fig.4 Comparison of correlation results of interval modes

取定一组关联航迹数据,在不同的最大测距系统误差下,比较近邻区间距离相对于原始数据近邻区间距离的增量。从图5中可以看出,由于副对角线方向两个局部节点传感器的最大系统误差差值不变,故近邻区间距离增量保持一致。而主对角线方向系统误差的差值对称变化,故近邻区间距离增量呈对称变化。如图4所示,双侧区间化处理后数据的不确定度较大,其近邻区间距离增量大约是单侧区间化的两倍,但对于不同大小的系统误差,两种区间化方式导致的增量变化趋势相同。在利用最小近邻区间距离进行关联判别时,取决于距离的相对大小而非绝对大小,故两种区间化方式下近邻区间距离增量的变化趋势相同决定了其关联效果相当。

图5 k近邻区间距离增量对比Fig.5 Comparison of increments of k-nearest neighbors interval dispersion

3.4 算法性能比较与分析

在仿真环境中,设置局部节点1传感器测距和测角的最大系统误差分别为1 000 m,1°,局部节点2传感器取不同的最大系统误差,比较算法的抗差性能,结果如表2所示。表中，为正确关联率,为错误关联率,为漏关联率。选取文献[26]算法与本文算法进行性能对比。

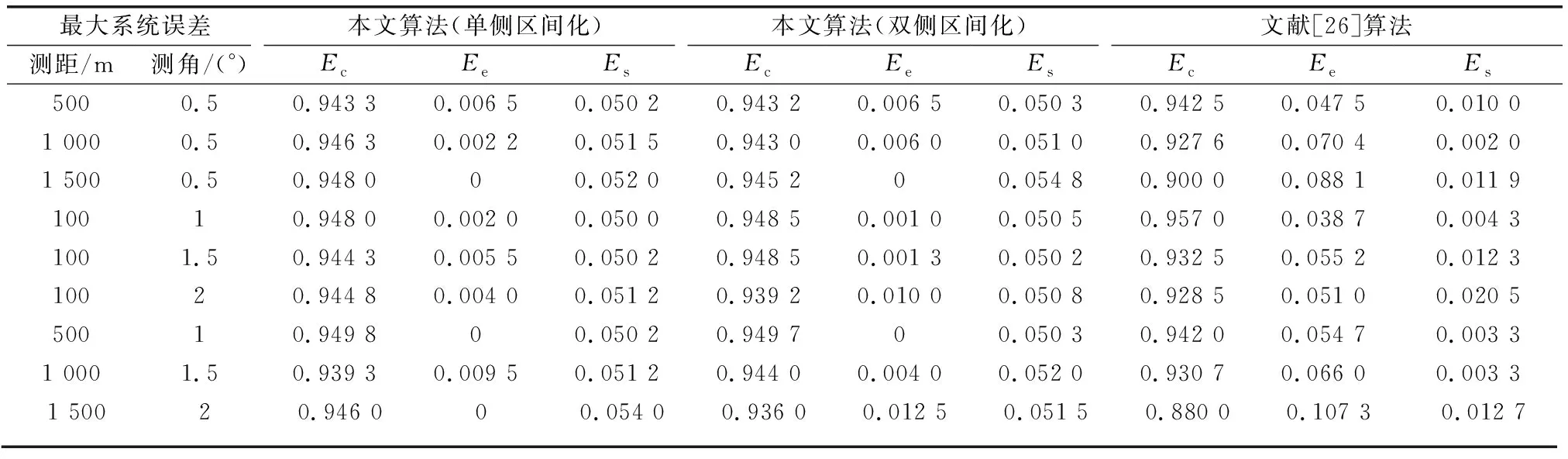
表2 不同最大系统误差下的正确关联率

由表2可以看出,不论是最大距离误差还是最大角度误差,随着最大系统误差的逐渐增加,文献[26]中算法的正确关联率有所下降,因为文献[26]算法通过对航迹序列中两两对应的航迹点计算距离组成相离度矩阵进行航迹关联判断,系统误差的增大会使航迹点的区间灰数范围扩大,导致带系统误差的航迹距离与航迹实际距离产生较大偏差;而本文算法选取整段距离最近的个平均区间距离,具有良好的抗差性能,因此一直保持较高的正确关联率。

另外,在判决关联结果是否归属漏关联时,本文算法通过反复试验最终确定的漏关联阈值门限是一个变化值,与航迹对具体关联度有关,而文献[26]算法采取固定值作为阈值门限,相对于变化的阈值门限更加稳定,因此本文算法的漏关联率比文献[26]算法高。

局部节点传感器开始采样时机或采样频率的不同易造成航迹的异步不等速率,而传统关联算法的假设前提中,航迹异步或系统误差只存在其一。在仿真环境中,保持局部节点1,2传感器测距和测角的最大系统误差为1 000 m,1°,研究航迹异步的影响。

由于文献[26]算法是以航迹同步为前提的抗差关联算法,只能在所有航迹序列等长且时间戳一致情况下进行关联,因此在实验前先对文献[26]算法进行时域配准预处理,使其适应航迹异步环境。

从表3中可以看出,采样周期以及开机时机不同对文献[26]算法的正确关联率影响较大,这是因为对文献[26]算法进行同步化处理会引入不必要的误差,影响总体关联质量;而本文算法中度量指标近邻区间距离的求解是在航迹点与航迹序列间寻找相对较近的距离,并未利用时间信息,也不要求航迹序列等长,航迹异步并不会改变各航迹序列对的近邻区间距离值,因此本文算法的关联效果没有受到影响。

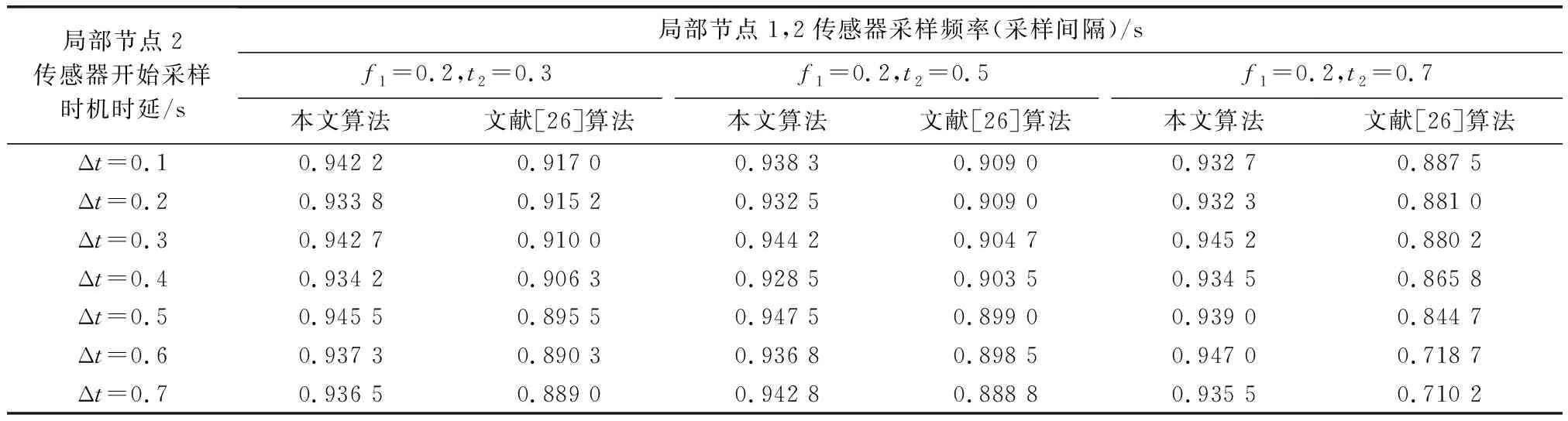
表3 不同采样频率和开始采样时机的正确关联率

3.5 算法复杂度分析

以同等长度的航迹序列为前提,表4比较了文献[26]算法和本文算法的乘法、加法运算量,表中为航迹批数,为航迹点数,为本文算法近邻区间距离的变量。

表4 算法运算量对比

在实际运算中,乘法耗时会大于加法耗时,显然,本文算法运算量要高于文献[26]中算法。这是因为文献[26]算法只解决了系统误差下的航迹关联问题,而本文算法可在异步和系统误差并存情况下直接关联,在处理异步航迹时,利用区间距离信息需要一定的计算量。另外,本文算法的单侧区间化与双侧区间化只是对数据的预处理方式不同,因而单、双侧区间化的运算量相同。

图6比较了不同航迹数目下各算法的耗时。可以看出,随着航迹数目的增加,本文提出的两种区间化处理方式耗时相当,但整体而言,本文算法耗时高于文献[26]中算法,结果与表4中的理论分析吻合。

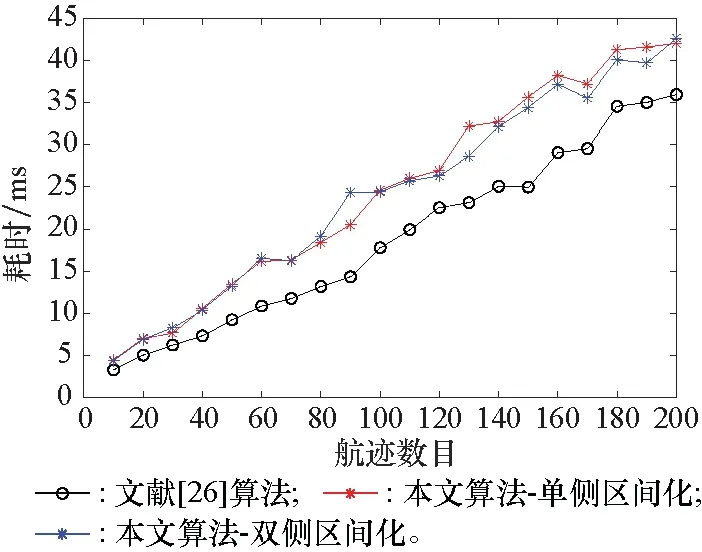
图6 不同航迹数目下的耗时对比Fig.6 Time-consuming comparison under different track numbers

4 结 论

本文提出一种利用近邻区间距离的异步抗差关联算法,定义区间坐标序列与区间坐标点间的近邻区间距离,并给出系统误差区间化方法。对系统误差先验信息的要求低,具有良好的抗差性能,且算法可不做时域配准直接处理航迹异步问题。