一种工业机器人多目标轨迹优化算法

李 琴，贾英崎，黄玉峰，李 刚，叶 闯

（1.西南石油大学机电工程学院，四川 成都 610500；2.中国石油天然气集团有限公司东方地球物理勘探有限责任公司，河北 涿州 072750）

近几十年来，随着自动化技术的飞速发展，工业机器人在生产线上的应用愈加广泛。轨迹规划是机器人运动控制的基础，良好的轨迹规划可以提高机器人的工作效率、降低机器人的能耗以及延长机器人的使用寿命。

目前，针对机器人轨迹规划优化的研究主要集中于采用多种算法相结合或改进原算法来获取最优的规划轨迹。例如：居鹤华等［1］根据机械臂的运动学约束，采用遗传算法对3-5-3多项式进行轨迹优化，但是3-5-3多项式存在加加速度突变的问题，且传统遗传算法容易使解陷入局部最优。Huang等［2］以5次非均匀有理B样条（non-uniform rational B-splines，NURBS）曲线作为工业机器人的轨迹规划曲线，并采用非支配排序遗传算法-II（non-dominated sorting genetic algorithm-II，NSGA-II）对运动时间和冲击磨损这2个目标进行优化，结果表明基于5次NURBS曲线构造的轨迹曲线较平滑，但未解决NSGA-II的不足，最终的结果仍易陷入局部最优。Rout等［3］提出了一种成就标量化函数与NSGA-II相结合的混合多目标算法，并对六轴工业机器人进行多目标轨迹优化，但采用的三次多项式并未实际解决机器人加速度、加加速度突变的问题。

基于此，笔者针对文献［1，3］中机器人加加速度不连续的问题，以工业机器人为研究对象，采用5次NURBS曲线作为其轨迹规划曲线，并结合布谷鸟搜索（cuckoo search，CS）算法中的Levy飞行策略与NSGA-II，提出了一种用于机器人多目标轨迹优化的混合算法（简称为CSNSGA-II），并对初始种群进行Tent混沌优化处理，最终得到分布均匀的Pareto最优解，旨在提高算法的收敛速度以及解决NSGA-II易陷入早熟的问题。

1 工业机器人多目标轨迹优化模型

在工业生产中，机器人通常按提前预设的轨迹进行移动，通过求解逆运动学方程得到机器人各关节的轨迹点位置矢量pi=[pi，1pi，2…pi，N]（i=0，1，…，n；3≤N≤6）。其中：i为关节的轨迹点，共n+1个；N为关节数，即自由度数。各关节的轨迹点构成了工业机器人的运行轨迹。

通常情况下，工业机器人在作业过程中大多会重复同一种动作。因此，为提高机器人的工作效率、降低机器人的能耗以及延长机器人的使用寿命，基于其运动学约束（速度、加速度和加加速度约束），定义目标函数［4］，可表示为：

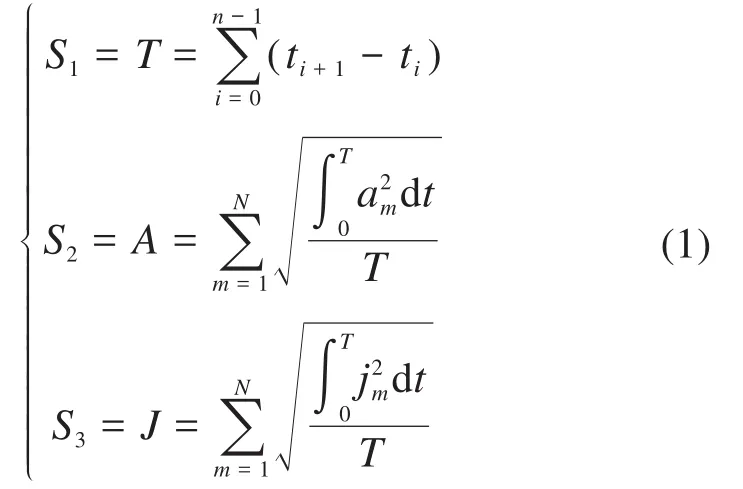
其中，约束条件为：

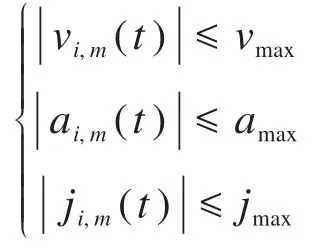
式中：S1(T)为机器人的总运动时间；S2(A)为机器人各关节加速度的平均值，用于衡量关节的能耗损失；S3(J)为机器人各关节加加速度的平均值，用于衡量关节的冲击损耗；ti为经过第i个轨迹点时所对应的时间；am、jm分别为机器人第m个关节的加速度和加加速度；vi，m、ai，m和ji，m分别为第i个轨迹点处机器人第m个关节的速度、加速度和加加速度；vmax、amax和jmax分别为机器人关节的速度、加速度和加加速度的最大值。

2 基于NURBS曲线的工业机器人轨迹规划

2.1 NURBS曲线的数学表示

根据工业机器人某一关节经过的轨迹点位置pi（i=0，1，…，n），采用k次NURBS曲线来规划其轨迹曲线。k次NURBS曲线可表示为分段有理多项式函数形式：

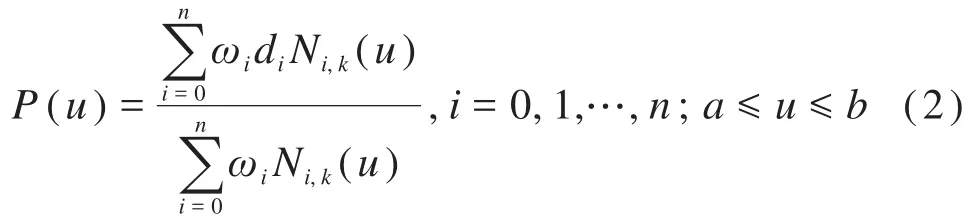
式中：P(u)为分段有理多项式函数；ωi为NURBS曲线的权因子；di为NURBS曲线的控制顶点位置；Ni，k(u)为k次NURBS曲线的B样条有理基函数。

Ni，k(u)是由节点矢量U=[u0u1…un+2k]按Cox De Boor递推公式推导得到的（规定0/0=0），可表示为：

设给定的轨迹点共有n+1个，为使机器人各关节经过给定的轨迹点，使k次NURBS曲线各分段的连接点与轨迹点一一对应，则需反求NURBS曲线的控制顶点。k次NURBS曲线由n+k个控制顶点与n+2k+1个节点组成。对于节点矢量U=[u0u1…un+2k]，本文采用规范节点矢量，即令u0=u1=…=uk=0，un+k=un+k+1=…=un+2k=1，其他节点均采用积累弦长参数化法对时间间隔矢量进行归一化求解获得：

式中：Δtj为轨迹点间的时间间隔。

2.2 5次NURBS曲线的控制顶点反算

由于3次NURBS曲线存在加加速度不连续变化的情况，本文采用5次NURBS曲线作为工业机器人的轨迹规划曲线。但是，5次NURBS曲线的插值数据量庞大，因此本文主要推导NURBS曲线的矩阵表达式，以简化计算过程。

基于上文推导的节点矢量U=[u0u1…un+2k]和轨迹点位置pi(i=0，1，…，n)，根据节点矢量、轨迹点与控制顶点的关系，反求5次NURBS曲线的控制顶点。由B样条曲线的局部支撑性可知，5次NURBS曲线在节点区间ui≤u≤ui+1内可表示为：

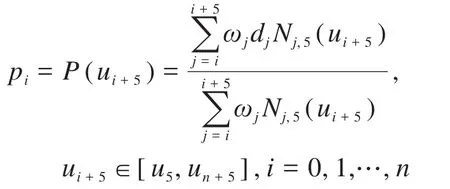
为方便计算，令第i（i≠0）段曲线为：

由Cox De Boor递推公式推导得到Ni中第1行的元素，分别为：

规定：

根据5次NURBS曲线的插值要求，可得：

其中，对于Qi(t)，当u=ui时，t=0；u=ui+1时，t=1。联立式（5）和式（6）可得：

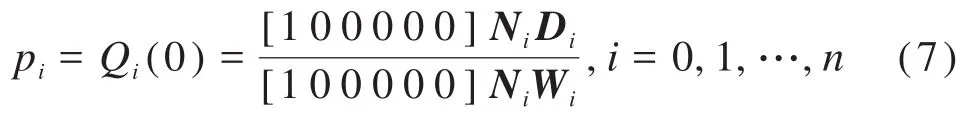
令 ：ai+2=n11ωi，bi+2=n12ωi+1，ci+2=n13ωi+2；ei+2=n14ωi+3，fi+2=n15ωi+4；qi=(ai+2+bi+2+ci+2+ei+2+fi+2)pi，则式（7）可以简化为：

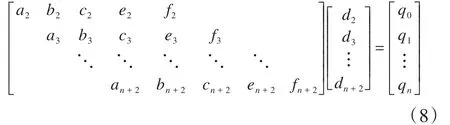
由式（8）构成的矩阵可以得出n+1个线性方程组，而所求的控制顶点为n+5个，根据线性方程组有唯一解的条件，还须根据边界条件确定4个附加方程。指定启、停速度为vs、ve以及启、停加速度为as、ae，并以启、停位置处5次NURBS曲线的一阶和二阶导数作为边界条件构建方程。

k次NURBS曲线的求导公式为：

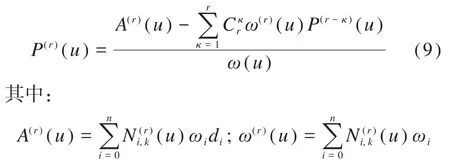
对5次NURBS曲线进行一阶、二阶求导，可得启、停时刻的速度vs、ve和加速度as、ae：

由于直接求导法的计算量较大且过程复杂，本文通过德布尔递推算法计算各阶导数的控制点。NURBS曲线上某一点的r阶导数P(r)(u)为：

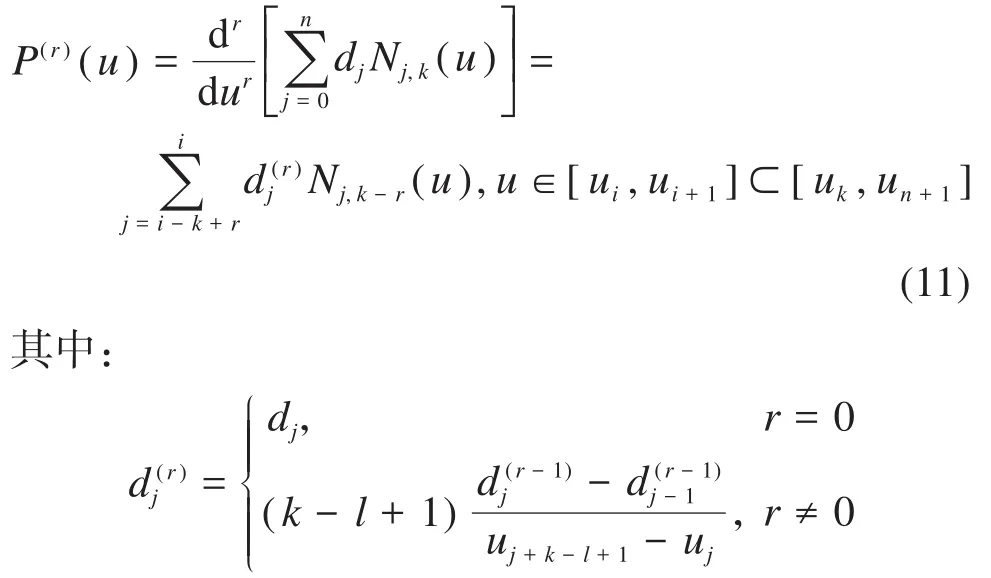
结合式（10）和式（11），对上文的n+5个线性方程进行求解，由此得到5次NURBS曲线控制顶点的位置矢量：

3 CSNSGA-II构建

NSGA-II是目前在多目标优化问题中应用最为广泛的算法之一，其是在NSGA的基础上引入快速非支配排序方法，并结合精英策略，利用其对某些测试函数进行优化可收敛到真正的最优Pareto前沿。但随着多目标优化问题的复杂性增加，传统的NSGA-II出现了不足之处，主要体现在以下2个方面［5］：1）易出现局部早熟的情况；2）搜索后期会出现局部搜索能力不足等。因此，须对NSGA-II进行改进，以获取更加真实且均匀的Pareto前沿。

CS算法是一种新型的启发式算法，由Yang和Deb于2009年提出［6］。研究表明，CS算法具有局部和全局搜索性能，基于其获得的最优解大多优于遗传算法和粒子群优化算法［7］，且已有较多的学者将CS算法应用于机器人轨迹优化［8-10］。基于此，提出了一种改进CS算法与NSGA-II相结合的CSNSGA-II，其中CS算法的Levy飞行策略可以帮助NSGA-II跳出局部最优，找到真实的Pareto前沿。

3.1 基于Tent混沌映射的种群初始化

为提高NSGA-II对工业机器人轨迹的优化性能，采用混沌算法对种群进行初始化。文献［4］采用一维logistic映射对种群进行初始化，但是一维logistic映射并不具有最好的遍历性，因此本文引入Tent混沌映射来产生初始种群。Tent混沌映射相比于logistic映射具有更好的均匀性与随机性［11］，可以提高算法的全局寻优能力。Tent混沌映射的表达式如下：

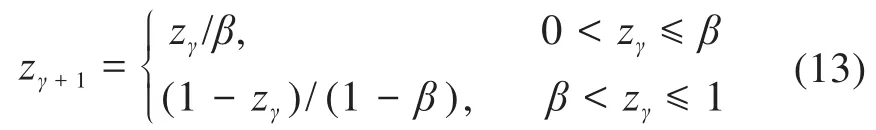
式中：β为混沌系数，取β=0.5；γ=1，2，…，v，v为决策变量数。

将混沌种群映射到对应的决策变量空间（tγmin，tγmax）中，得到初始种群的变量：

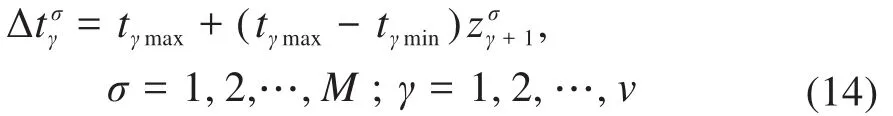
3.2 约束不可行度处理

在NSGA-II处理约束优化问题时，常用到对不可行度的处理，以保留与可行解接近的解，舍弃与可行解相差较大的解。为了使不等式约束转化为等式约束［12］，定义不可行度Cx（x=1，2，…，G，G为当前种群中解的数量）：

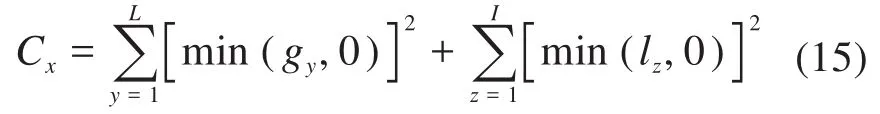
式中：gy、lz分别为不等式约束和等式约束；L、I分别为多目标优化模型中不等式和等式约束的数量。

不可行度Cx表示超过约束条件的距离，当个体在约束条件内时，Cx=0。

同时定义约束违规阈值Cxmean：

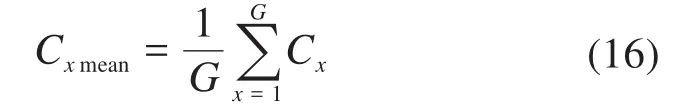
超过约束违规阈值的解定义为不可行解，满足约束违规阈值的解定义为可行解。

3.3 自适应Levy飞行策略

传统CS算法中的Levy飞行策略存在种群多样性不易调节、搜索方式不能合理控制等问题，导致该算法的精度不高及收敛速度较慢，因此本文提出了一种自适应Levy飞行策略，其表达式如下：

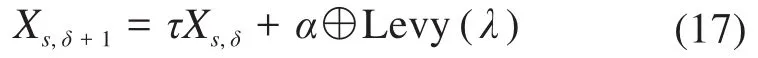
式中：Xs，δ为第s只布谷鸟的第δ代鸟巢的位置；τ为动态惯性权重；α为变步长因子；⊕表示矩阵之间的各元素对应相乘，Levy(λ)为Levy随机搜索策略。

Levy随机搜索策略可表示为：

式中：U、V服从标准正态分布，μ=1.5。

动态惯性权重τ越大，CS算法的全局搜索能力越好；相反，τ越小全局搜索能力越差。因此采用自动调整惯性权重的方法，以使算法初期即具有较好的搜索能力。τ的表达式为：

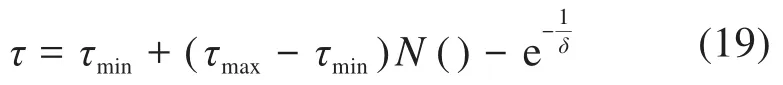
式中：τmax为惯性权重的最大值；τmin为惯性权重的最小值；N()为服从(0，1)上均匀分布的随机数。

变步长因子α可表示为：

其中：

式中：Xs，best为随机选取的当前Pareto前沿的最优解；δmax为最大迭代次数。

3.4 CSNSGA-II流程

本文所提出的CSNSGA-II的流程如图1所示，其中遗传操作中的交叉算子采用独立点交叉算子，变异算子采用多项式变异算子。

图1 CSNSGA-II流程Fig.1 Flow chart of CSNSGA-II

由图1可知，CSNSGA-II的具体步骤为：

步骤1 设定交叉、变异系数。采用Tent混沌映射生成初始化时间种群，并计算种群的适应度函数，在进行非支配排序后对排序后的解集进行拥挤距离计算，并按照拥挤距离进行排序。

步骤2 对排序后的所有解进行不可行度计算，得到可行解集W1和不可行解集V1。

步骤3 对可行解集W1进行二联锦标赛选择，对筛选的解进行下一代的交叉、变异操作，最终得到可行解集W2。

步骤4 采用自适应Levy飞行策略对不可行解集V1进行更新，得到新的解集V2。

步骤5 将解集W2与解集V2合并，并对新解集进行适应度计算、非支配排序和拥挤距离计算。

步骤6 重复步骤2、3和4，直到满足结束条件。

4 6R勃朗特机器人多目标轨迹优化仿真分析

4.1 仿真参数设置

在MATLAB软件中对6R勃朗特机器人（见图2）进行运动学建模，并采用本文提出的CSNSGA-II对其轨迹进行优化。设置6R勃朗特机器人启、停时刻的位置（笛卡尔坐标系中），并采用5次NURBS曲线构建其关节的轨迹，同时定义启、停时刻的速度、加速度均为0，指定5次NURBS曲线的各项权因子均为1，初始化种群数量为200，最大迭代次数为100次。根据经验，遗传算法的交叉概率设为0.6，变异概率设为0.1。6R勃朗特机器人各关节轨迹点的位置如表1所示，基于MATLAB软件可得其启、停时刻位置分别如图3和图4所示，各关节的运动学约束如表2所示。

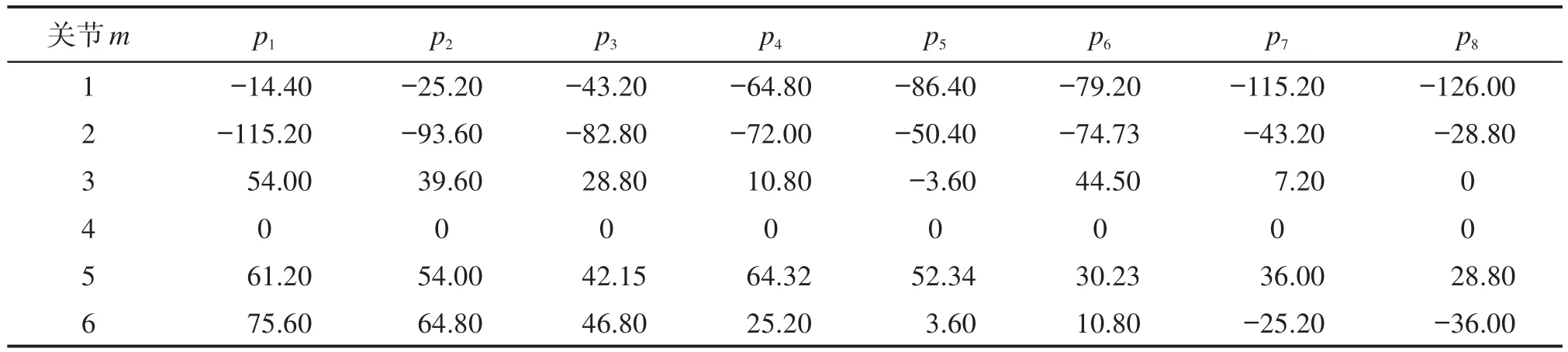
表1 6R勃朗特机器人各关节轨迹点的位置Table 1 Position of each joint trajectory point of 6R Bronte robot 单位：（°）

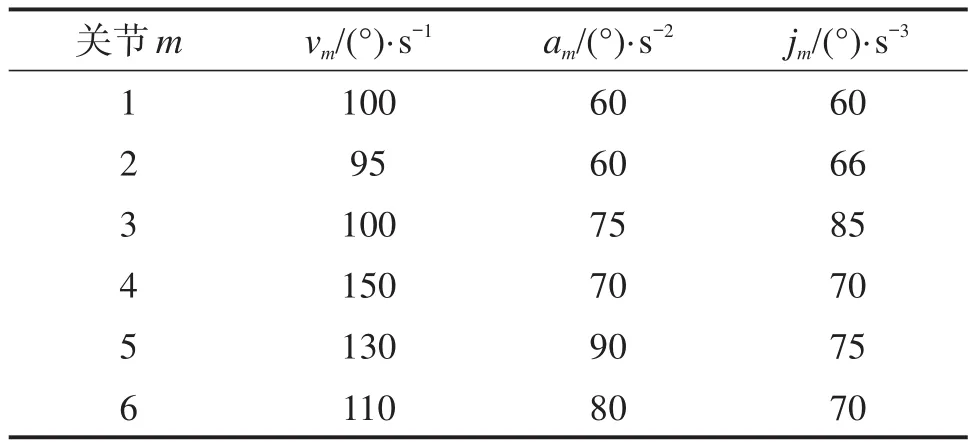
表2 6R勃朗特机器人各关节的运动学约束Table 2 Kinematic constraints of each joint of 6R Bronte robot

图2 6R勃朗特机器人实物Fig.2 Physical object of 6R Bronte robot

图3 6R勃朗特机器人启动时刻的位置Fig.3 Position of 6R Bronte robot at the moment of start

图4 6R勃朗特机器人停止时刻的位置Fig.4 Position of 6R Bronte robot at the moment of stop

4.2 仿真结果分析

图5所示为分别采用CSNSGA-II、NSGA-II和多目标粒子群优化（multi-objective particle swarm optimization，MOPSO）算法对6R勃朗特机器人进行轨迹优化后得到的Pareto前沿分布结果。从图中可以看出：相比于NSGA-II、MOPSO算法，基于CSNSGA-II得到的Pareto前沿分布得更加均匀，且更加靠近真实的Pareto前沿。

图5 基于不同算法的6R勃朗特机器人Pareto前沿分布对比Fig.5 Comparison of Pareto front distribution of 6R Bronte robot based on different algorithms

为了进一步验证CSNSGA-II的优势，在基于3种算法优化后获得的6R勃朗特机器人Pareto前沿中分别取3组解，结果如表3所示。其中：A1、B1、C1为CSNSGA-II优化后得到的3组解；A2、B2、C2为NSGA-II优化后得到的3组解；A3、B3、C3为MOPSO算法优化后得到的3组解。通过对比分析可得出，解A1支配解A2、A3，解B1支配解B2、B3，解C1、C2、C3互为非支配解。结果表明，相比于NSGA-II、MOPSO算法，基于CSNSGA-II能得到更优的Pareto前沿。

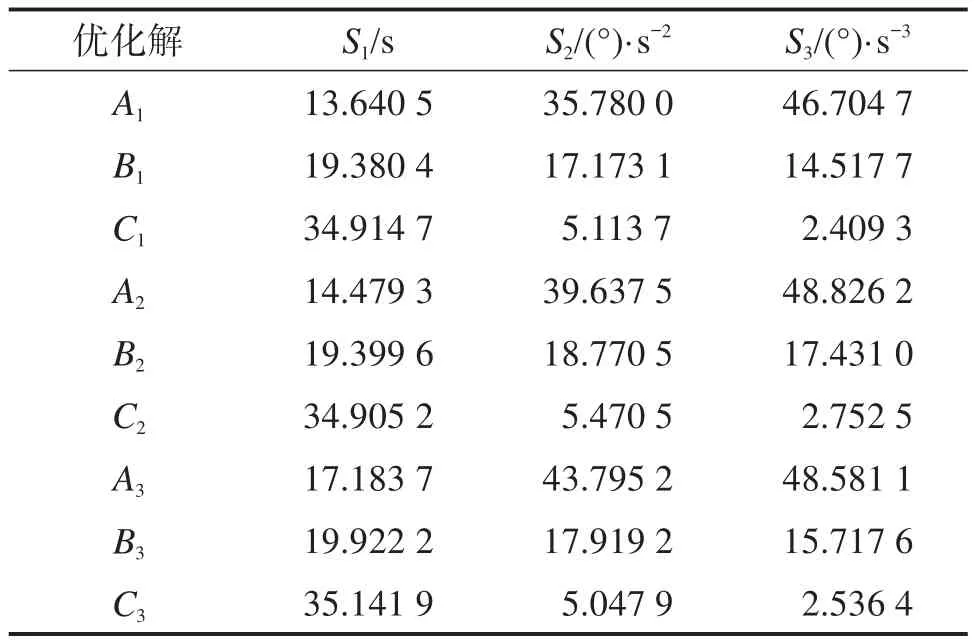
表3 基于不同算法的6R勃朗特机器人轨迹优化结果对比Table 3 Comparison of trajectory optimization results of 6R Bronte robot based on different algorithms

为了进一步分析CSNSGA-II的收敛性能，给定一个优化目标综合函数S：

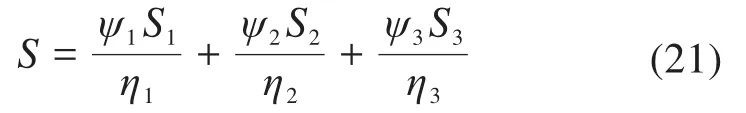
式中：ψ1、ψ2、ψ3为加权因子，在实际生产应用中，根据用户的需求可以确定各加权因子的系数。在本文中，为了对比算法收敛的速度和收敛性能，取ψ1=ψ2=ψ3=1，η1=1，η2=100，η3=100。

利用式（21）计算得到基于不同算法的6R勃朗特机器人轨迹优化目标的归一化加权迭代最优值，对比结果如图6所示。图6结果显示，基于CSNSGA-II得到的机器人轨迹优化目标的最优值优于基于NSGA-II和MOPSO算法的，由此说明CSNSGA-II有助于跳出局部最优，且CSNSGA-II达到稳定收敛时的迭代次数比NSGA-II和MOPSO算法分别减少了63.16%和59.62%，有效提高了优化效率。

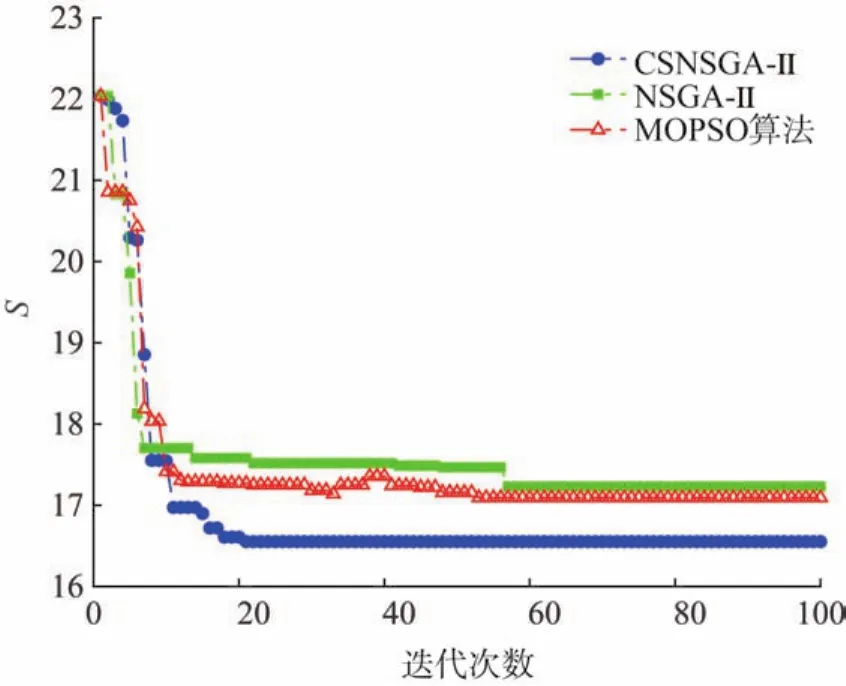
图6 基于不同算法的6R勃朗特机器人轨迹优化目标归一化加权迭代最优值对比Fig.6 Comparison of normalized weighted iterative optimal values of trajectory optimization objectives of 6R Bronte robot based on different algorithms

取解B1对应的时间间隔矢量Δt=［0 5.059 7 3.231 5 1.609 9 1.309 8 2.495 2 1.988 1 3.686 2］，其对应5次NURBS曲线的节点矢量U=［0000 0 0 0.261 0 0.427 8 0.510 9 0.578 4 0.707 2 0.809 7 1 1 1 1 1 1］，其对应的各关节的位置、速度、加速度和加加速度随时间的变化曲线如图7至图10所示。从图中可以看出，利用CSNSGA-II优化后，6R勃朗特机器人各关节的运动轨迹平滑且无冲击，相比于文献［13-15］所得结果更具有平稳性。

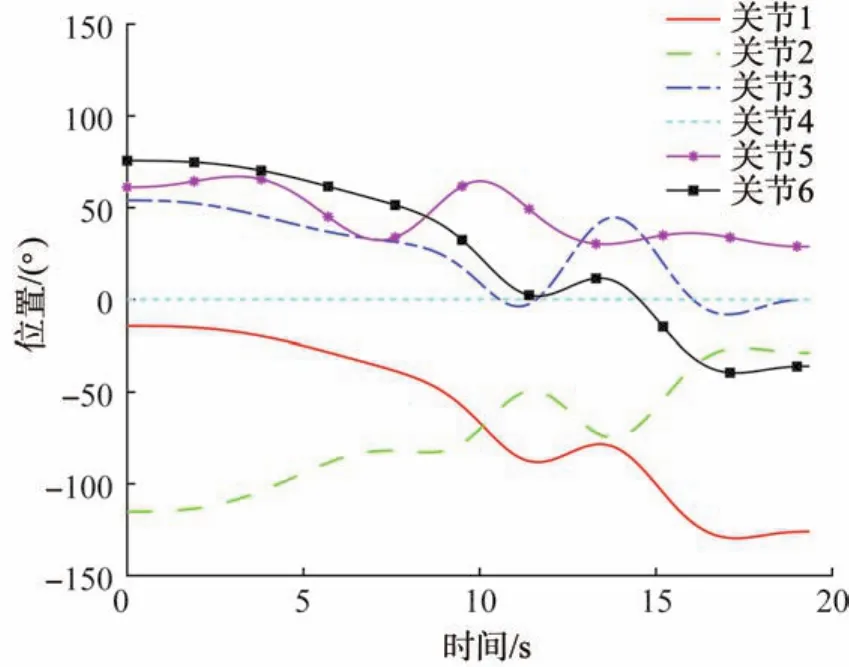
图7 6R勃朗特机器人各关节的位置—时间曲线Fig.7 Position-time curve of each joint of 6R Bronte robot

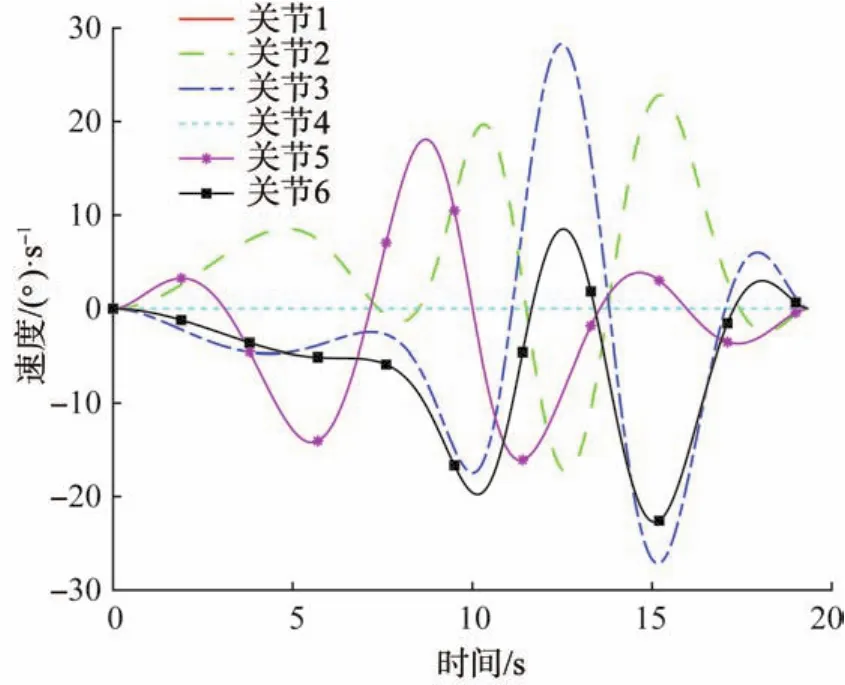
图8 6R勃朗特机器人各关节的速度—时间曲线Fig.8 Velocity-time curve of each joint of 6R Bronte robot

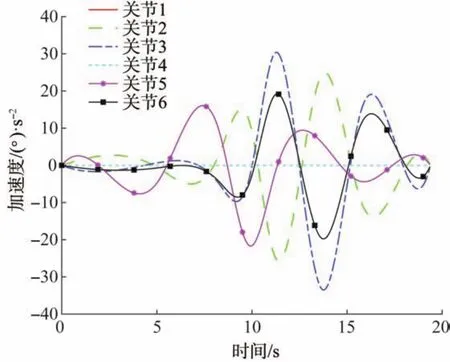
图9 6R勃朗特机器人各关节的加速度—时间曲线Fig.9 Acceleration-time curve of each joint of 6R Bronte robot

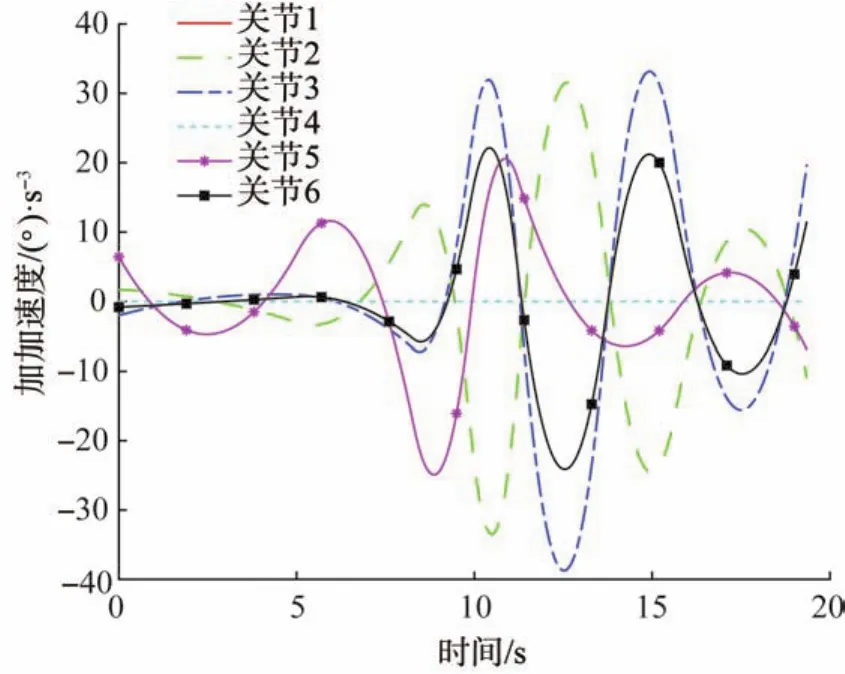
图10 6R勃朗特机器人各关节的加加速度—时间曲线Fig.10 Jerk-time curve of each joint of 6R Bronte robot

5 总 结

本文采用5次NURBS曲线作为工业机器人的轨迹规划曲线，以运动时间、能耗、冲击磨损这3个指标作为优化目标，并在运动学约束下进行优化求解。提出了一种基于改进CS算法与NSGA-II结合的混合算法——CSNSGA-II。通过对6R勃朗特机器人的轨迹进行优化后可知，CSNSGA-II能成功地跳出局部最优，解决了NSGA-II易陷入“早熟”的问题，同时基于该算法得到的Pareto前沿分布得更加均匀，有效提高了收敛速度。结果表明，所提出的CSNSGA-II具有较高的实用价值，可为工业机器人高效、持久、可靠地作业提供指导。