运用有效策略 渗透模型思想

文|孙保华

渗透数学模型思想，就是针对抽象的数学概念和命题，引导学生在情境中展开数学抽象活动，利用学生能够理解的具体实例来说明，通过实例来帮助其理解抽象的数学知识。因此教师要引领学生经历建模的全过程，从相对简单到相对复杂、从相对具体到相对抽象，慢慢积累经验，探索解决问题的基本途径，促进学生对数学模型的理解，感悟模型思想，体验模型的价值，提升其应用数学模型的意识和能力。

一、多维感知，充分体验

数学模型是解决一类问题的基本数量关系结构，其本质是从单个问题的解决抽象到一类实际问题的解决，关注的对象是具有共性的一类事物，因此教师要给学生提供丰富的感性材料，让其能够多侧面、多维度感知这类对象的特征或数量关系，把握其中蕴含的共同特征、结构，归纳、提炼解决问题的基本模型。

例如，苏教版四年级下册《乘法分配律》的教学，可以围绕“运动会”设置一个情境串。

情境一：学校进行跳绳比赛，四年级有6个班，五年级有4个班，每个班都领取12根跳绳，四、五年级一共要领多少根跳绳？

师：要求一共要领多少根跳绳，可以怎样列式计算？

生：12×6+12×4=120（根）。

生：12×（6+4）=120（根）。

师：因为这两个算式的结果都是120，所以我们可以用等号把这两个算式连接起来组成一个等式。

师：谁能说一说这两个算式表示的意义？

生：在第一个算式中，12×6表示四年级一共领取的跳绳根数，12×4表示五年级一共领取的跳绳根数，也就是分别算出两个年级一共领取的跳绳根数，再合起来就表示四、五年级一共领取的跳绳根数。

生：在第二个算式中，6+4表示四、五年级一共的班级数，再乘12，就表示四、五年级一共领取的跳绳根数。

师：这是两种不同的思路，所以可以列出两个不同的算式。

教师结合图示引导学生说说想法。

生：12×6表示6个12，12×4表示4个12，合起来就是10个12，而12×（6+4）就表示10个12，因此这两个算式的结果是相等的。

师：这位同学是从乘法的意义来理解这两个算式都表示10个12，所以不计算就知道它们的结果是相等的。

……

很多教师在教学中往往只会出示上述这一素材，学生感知是不够丰富的，不利于学生对乘法分配律这一模型的正确建构。所以可以再出示下面两个素材继续让学生自主探究。

情境二：四、五年级需要购买一批运动服，上衣每件需85元，裤子每条需55元，购买6套这样的运动服共需多少元？

情境三：加工这样的一套运动服需要用多少布料？（如下图）

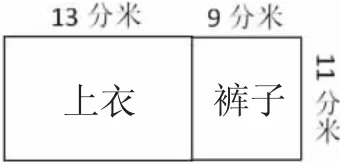
生活情境中的不同问题有助于学生比较、分析，扬弃非本质属性，形成对乘法分配律的深刻认识。在模型的建立过程中可以多层次引导学生进行感知：先让学生列式计算比较，由结果相等得到等式；接着让学生进行事理的数学概括，表述自己的解题思路；然后引导学生由事理向算理演变，用乘法的意义进行解释；最后进行模型的猜想和验证，引导学生建立正确的数学模型。

二、多元表征，展现过程

在教学中教师要让学生充分感知素材并结合学生已有的认知和生活经验，鼓励自主探究，适时引导学生用显现的方式表征模型。同时每个学生的认知水平不同，思维方式各异，解决问题的思路不相同，表征模型的方式也不尽相同，而多元表征正是学生个性化解读与理解的过程。因此教师在教学过程中要让学生有交流的机会，充分展示其思维过程并多元表征数学模型，这样不仅有利于丰富学生对知识内涵的理解，也有利于学生加深对模型结构的认识。

例如，苏教版六年级下册《解决问题的策略》的教学，解决如下一个实际问题：鸡和兔一共有8只，它们的腿有22条，鸡和兔各有多少只？

师：现在你们能用自己的方法来解决“鸡和兔各有几只”吗？

生：我用画图的方法。

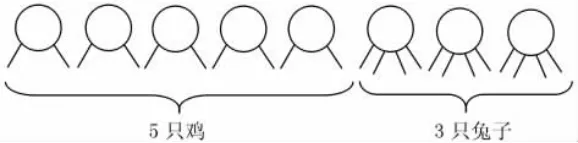
在表征的过程中，有些学生是把8个圆都看成兔，先画出了32只脚后，再擦去多算的10只脚；还有些学生是把8个圆都看成鸡，先画出了16只脚后，再添加少算的6只脚。

生：我用列表的方法。

?

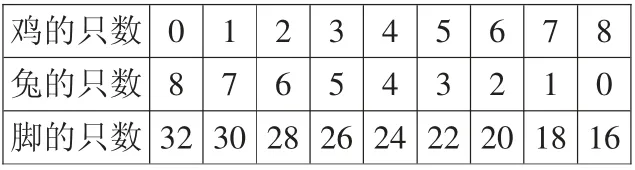
生：我用列方程（一元一次）的方法。

解1：设兔有x只。

4x+2（8-x）=22

解2：设鸡有x只。

2x+4（8-x）=22

生：我也是用列方程（二元一次）的方法。

（鸡的只数）×2+（兔的只数）×4=22

鸡的只数+兔的只数=8

生：我用的是算术方法。

假设8只全部是兔。

4×8=32（只）

32-22=10（只）

4-2=2（只）

10÷2=5（只）……鸡的只数

8-5=3（只）……兔的只数

生：我用的也是算术方法。

假设8只全部是鸡。

2×8=16（只）

22-16=6（只）

4-2=2（只）

6÷2=3（只）……兔的只数

8-3=5（只）……鸡的只数

学生在解决“鸡和兔各有几只”的问题时，可以用画图来表征，也可以用列表来呈现思考过程，还可以用代数思维（一元一次方程和二元一次方程）或算术思维（假设法）来解决问题。同时每一种方法背后都有两种思考的顺序，可以从假设8只都是鸡开始推理，也可以从假设8只都是兔开始推理。总之，教师对素材的合理开发，让学生进行个性化的多元表征，不仅可以满足不同层次学生的认知能力和学习需求，还可以让学生实现模型的自主建构。

三、适度变式，强化结构

学生经历建模的过程，本质上就是“数学化”的过程，是学生在学习中获得带有“模型”意义的数学结构的过程。当学生经历了建模过程，抽象、概括得到某一数学模型后，教师要将数学模型适度的变式，引导学生比较各种情况之间的联系，从而使建构的数学模型内涵不断得到丰厚。同时也有助于学生感悟原型间的联系，强化模型结构，体会数学结构的魅力。

例如，苏教版三年级上册《间隔排列》的教学。

师：把△和○一个隔一个地排成一行，如果△有8个，○最少需要多少个？最多需要多少个？请同学们尝试去摆一摆，画一画。

生：我发现如果两端物体不同（如下图），○则需要8个。

△○△○△○△○△○△○△○△○

○△○△○△○△○△○△○△○△

生：我发现如果两端物体都是△（如下图），○则需要7个。

△○△○△○△○△○△○△○△

师：如果两端都是○呢？

生：如果两端都是○（如下图），○则需要9个。

○△○△○△○△○△○△○△○△○

师：请同学们仔细观察，把△和○一个隔一个地排成一行，共出现了几种情况？

生：一共出现了三种情况。

生：一种是○的个数比△少1，即○有7个。

生：一种是○的个数与△同样多，即○有8个。

生：一种是○的个数比△多1，即○有9个。

生：我发现○最少需要7个，最多需要9个。

师：一一间隔排列的两种物体，在什么情况下两种物体的数量相等，在什么情况下两种物体的数量相差1？

生：如果两端物体不同，两种物体的数量正好相等。

生：如果两端物体相同，两种物体的数量相差1。

这样的教学充分利用各种数学问题串成问题链，形成系列化的思维变式资源。引导学生通过操作得出结论，从不同角度加深体验，以进一步完善对间隔排列的两种物体间数量关系的认识，进一步认识间隔排列的规律，从而帮助学生强化并丰富了模型结构。

四、有效拓展，推广应用

模型思想的渗透，要从具体、形象的实例或现实情境开始，通过多次的抽象、概括，帮助学生建立数学模型。同时要引导学生通过思维发散和联想将模型加以扩展和推广。因此我们要将一个问题的解决，拓展为解决一类问题，帮助学生运用归纳推理，由特殊到一般，逐步逼近问题的本质，运用该模型解决问题并加以推广应用。

例如，苏教版五年级上册《用字母表示数》的教学，用小棒照样子摆一行三角形。

?

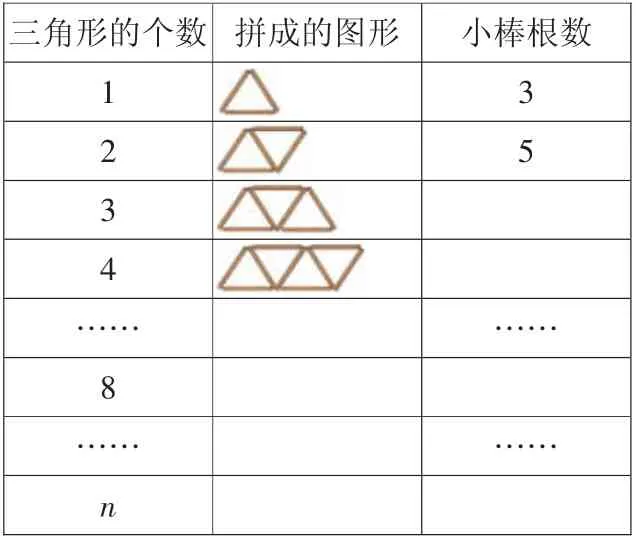
师：请同学们把表格填写完整，如有困难就用小棒摆一摆。

师：请同学们仔细观察表格中的数据，你有什么发现？

生：我发现摆8个三角形需17根小棒，先算增加的7个三角形需2×7=14根，再加上第一个三角形的3根，共17根。

生：我发现摆10个三角形需21根小棒，把每个三角形都看作需要2根小棒就是2×10=20根，再加上第一个三角形的1根小棒，共21根。

生：我还发现摆n个三角形需3+2（n-1）根小棒，每增加一个三角形需2根小棒，多摆n个三角形需增加2（n-1）根小棒，再加上第一个三角形的3根小棒就可以了。

生：我发现摆n个三角形需2n+1根小棒，即每增加一个三角形都需要2根小棒，最后再补开头三角形的1根小棒就可以了。

师：刚才几位同学说得都非常好。我们发现可以用3+2（n-1）或2n+1来表示一共需要的小棒根数。

学生解决了摆n个三角形所需小棒的根数，并建立了这一实际问题的数学模型。一般教学不能到此为止，还需进一步推广。教师顺势又出示一组题让学生尝试解决。

连续摆n个正方形，要（ ）根小棒。

连续摆n个五边形，要（ ）根小棒。

连续摆n个六边形，要（ ）根小棒。

连续摆n个a边形，要（ ）根小棒。

学生经历建模过程后，教师组织学生将此数学模型进一步拓展和迁移，多数学生能够以此类推，写出一般的表达式（a-1）n+1，使已经构建的数学模型不断得到丰富，有助于学生加深对此模型内涵的理解。

总之，在教学中要运用各种有效的策略，让学生经历知识的形成过程，成功构建好一个个数学模型，形成结构化的知识，才能让学生在解决问题的过程中，识别模型、运用模型，理解模型的价值，感受数学的魅力。