深入理解教材 把握方程本质——《方程的意义》一课教材解读

文|何海滨

读懂教材是实现有效教学的前提，在读懂教材的同时，要深入把握知识的本质，才能准确提炼有助于学生深度学习的核心问题。下面以人教版教材《方程的意义》一课为例，谈谈如何在解读教材中把握本质，有效提炼核心问题。

一、沟通联系，借实物来理解等式

方程是含有未知数的等式，认识等式是认识方程的前提。等式是方程的生长点，教学方程的概念要从等式引入。在学生的日常学习中，经常接触等式，这时的等式多数是对某个式子运算而得出来，例如为计算“12+20”这一式子得到“12+20=32”这一等式。此时，学生对等式“32”的认知是一个算式的计算结果，式子与结果在学生的认知中更多的是因果关系的存在，对其等式的感知较为薄弱。表示两个量或两个表达式相等的式子叫做等式，小学生理解等式的含义、形成等式的概念并不容易。如何从已有的认知入手，让学生充分感受等式的这一特点，教材采用了天平这一实物，让学生从具体的情境中来理解抽象的数学算式，体验等式的含义。

借助天平能够直观地表现“相等”和“不相等”两种现象。天平的两个托盘相当于等式的左右两边，当天平平衡时，就表示两个托盘的物体质量相等，可以用等号连接两边物体的质量，从而形成等式。图1中借助天平展示左边有2个50g的砝码，右边有1个100g的砝码，左边代表的是“50+50”的式子，右边代表的是一个质量为“100”的量，两个托盘表示两种不同的意义，借助天平左右两边平衡，帮助学生建立两者之间的相等关系。图2则是通过发现空杯和100g的砝码刚好平衡，利用空杯与天平是方程的形象支撑，得出一只空杯质量为100g，这时学生感受到的是平衡就代表等量，可以借助天平平衡的特点来求解未知的量。

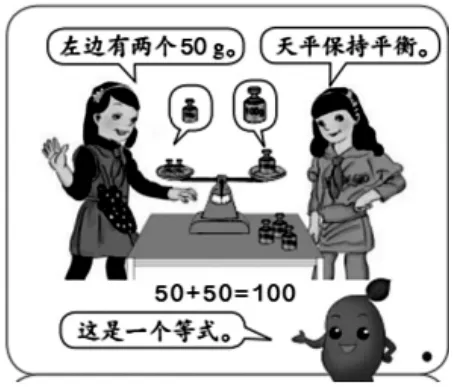
图1

图2

二、体验过程，在变化中感受关系

表示等量关系是形成方程的核心。学生形成关于方程的概念，不仅要知道方程是含有未知数的等式，更要体验方程能够表示数量之间的相等关系。认识方程的意义，不能局限于它的外在特点，还要凸显它是表示相等关系的一种数学形式。教材借助系列图，通过两种变化，让学生去感受数量之间的关系。

图3中学生向杯中加水，天平失衡。提出问题“如果水重xg，杯子和水共重……”由此引发学生对“一杯水水有多重”这一方程的主要因素——未知量的感知。

图3

图4则是分别添加100g砝码，发现天平左右失衡，得出100+x＞200和100+x＜300两个不等式。许多教师在这里存在着不解，方程的意义与等量有关，为什么要出现不等式？教材的意图并非为引入不等式，而是让学生带着“一杯水有多重”这一问题，借助两次调整砝码的过程，体验到天平左右两边的关系并未形成等量关系，因而等式不能成立，同时在过程中感受水的重量所在的区间，为等量关系的建立埋下伏笔——当呈现砝码为250g的时候，天平平衡了，学生在体验中得知“100+x”和250的相等关系，从而引导得出100+x=250。

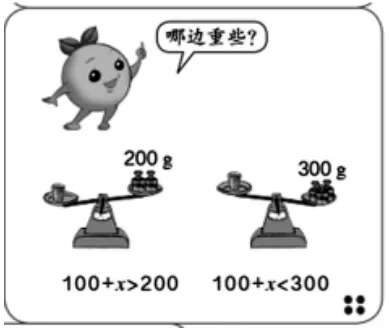
图4

教材借助情境图的变化，通过盘秤的情境，以等量关系蕴含在图画中的形式呈现方程的相关内容，让学生经历从相等到不等再到相等的过程，感受量与量之间的变化关系。既让学生探索隐含其中的等量关系，也使学生经历了用半符号语言表达等量关系、用未知数x来表达等量关系的过程，让学生在过程中感受方程的形成过程。

三、把握本质，在应用中建立模型

方程的内涵本质是什么？张奠宙教授指出：方程是为了寻求未知数，在未知数和已知数之间建立起来的等式关系。方程是描述客观世界中数量关系之间相等关系的数学模型。方程的本质是“关系”，而且是一个等量关系。方程是从现实生活到数学的一个提炼过程，一个用数学符号提炼现实生活中的特定关系的过程。在小学中方程不仅仅是一个概念而已，方程是有用的，是从现实情境到用自然语言等价地表达出来。方程的教学应该经历“生活中的提炼，到数学表达，到形式化的过程，再到最终解决方程问题”。

当学生借助天平的情境图理解等式与方程的关系后，教材从生活入手，出现了每本练习本x元，三本练习本一共2.4元的情境（如图5），这里把每本练习本的单价——“x元”当成一个量存在，但这是一个未知量，需要找到等量关系来列式解决，从而出现3x=2.4这一方程。在解决问题中理解数量关系，建立方程的模型——“像100+x=250；3x=2.4……这样含有未知数的等式就是方程”。

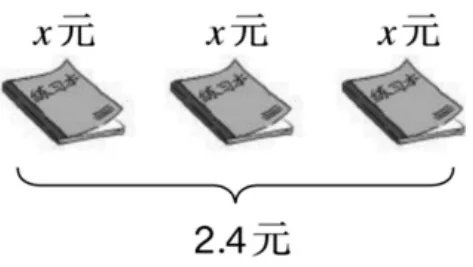
图5

四、深化思考，在理解中深刻认识

能顺利辨认方程的样子就是认识方程了吗？能流利地说出方程的定义就是理解方程了吗？这显然是狭隘的理解方程。

史宁中教授曾提到如何理解方程的定义问题，他说：“虽然教科书中定义为‘含有未知量的等式’，但应当知道方程的本质是在讲两个故事，这两个故事有一个共同点，在这个共同点上两个故事的数量相等。”也就是说，从定义出发去判断一个式子是不是方程，意义不大，关键是要知道方程是怎么回事，是做什么用的。而学生必须要掌握的是要用数学的符号把要说的话（即两件事情等价）表达出来。

如何理解史宁中教授的话，我们举一个例子来说，例如，从甲地到乙地，客车每小时行a千米，m小时到达。货车每小时行b千米，n小时到达。这里讲的是客车行驶和货车行驶的两件事，两件事的共同点是都从甲地到乙地，找到了共同点，就明白了两车所行的路程相等,也就有了a×m=b×n这一关系，不论速度和时间有什么变化，它们两者之间的等量关系是一直存在的，在解决问题的过程中，根据这个关系，我们就可以解决生活问题中的未知量。

在小学数学学习中，从算术思维到代数思维的过渡，对学生来说是思维方式上的一次飞跃。学生能否通过学习实现思维方式的转变，直接关系到学生未来的学习和发展。只有认真解读教材，基于方程的本质来理解方程的意义，才能促进学生思维的提升。