多层次构建活动平台 多维度发展学生思维——以《摆一摆 想一想》为例

文|胡晓娜

【教学内容】

人教版一年下册第51页。

【教学过程】

数学课堂是培养学生思维能力的主阵地。那么如何发展思维呢？笔者打磨了《摆一摆 想一想》一课，从预设、实施到改进，感悟到：教学中，如能多层次地构建活动平台，就能有梯度地提升学生多维度思维能力。

一、借助直观，培养抽象思维

片断一：初步操作，感受位值。

（课件出示一个小圆片和一张数位表）

师：这个小圆片很迷糊，不知道自己表示几，谁能帮帮它？

生：一个圆片表示1。

师：还能表示其他的数吗？

生：如果在十位，那就表示10。如果在个位，那就表示1。

师：这个小圆片好神奇呀，1个小圆片就能创造两个数。今天，我们就和神奇的小圆片一起玩游戏。（板书：摆一摆，想一想）

师：王国里又来了一个淘气的小圆片，那2个小圆片能创造出几个数呢？先静静思考，请一个同学上来摆一摆。

师：这位同学用2个小圆片能创造出3个数。

以上教学片断中，先让学生通过1个小圆片感受圆片摆在不同位置上就表示不同的数，初步感受“位值”，再用2个圆片摆出不同的数，教学记录方法。这个层次的探索操作，学生初步感受将具体事物抽象成数字，为后续更深层次的探究奠定了基础。

二、动作表征，发展有序思维

片断二：二次操作，学会有序思考。

师：现在又来了一个淘气的小圆片，你能摆出哪些数呢？

同桌合作：

1.取出3个小圆片，一个同学摆，一个同学记录在表格中。

2.完成表格后请把小圆片放回学具袋并用端正的坐姿告诉老师。

师：老师收集了4份作业。仔细观察，你喜欢哪一种，为什么？

作业1：3021123

作业2：3122130

作业3：1232130

作业4：3123021

生：我喜欢作业1、2，都有顺序。作业3、4没有顺序，好乱。

师：有顺序地摆能帮助我们不重复、不遗漏。请作业2的同学上来摆一摆，边摆边说你是怎么摆的。

师：谁注意到了他刚刚是怎么摆的？

生：都先放在个位上，再每次移一个到十位上，就能做到不重复也不遗漏。

师：你猜作业1刚开始都放在了哪？

生：十位。

师：猜对了吗？我请这位同学来移一移。

师：谢谢你的验证。现在，我们一起来回忆一下刚刚这位同学进行有序摆的过程，要想不重复也不遗漏，怎么办？

生：都先放在其中一个数位上，再一个一个移到另一边，直至全部移到另一边。

学生在这一层次的探索操作中，经历从无序到有序的思考过程。在一次次自主操作、看别人操作、优化自己的操作中，实现按顺序记录结果的可能。以“摆”助思，学生在“摆”中进一步感受位值，并学会了有序思考。

三、梳理总结，拓展归纳思维

片断三：深入思考，探索规律。

师：如果给你4个小圆片，你猜能摆几个数？你能不摆，直接画一画就创造出所有的数吗？

学生操作活动：都先放在（ ）位上，再每次移一个到（ ）位上。

师：你有什么发现？

生：我发现摆出来的数比圆片的数量多1个。

生：1个圆片摆出了2个数，2个圆片摆出了3个数……

师：所以，圆片的个数和摆出来的数的个数有什么关系？

生：圆片的个数+1=摆出的数的个数。

师：那5个圆片能摆出几个数？

生：6个数。

师：请你快速地不重复也不遗漏地写出这些数。

师：有位同学写出来的数是这样的：5、14、23、24、41、50。

生：不赞同！因为24是用6个小圆片摆出来的。

师：他说的是什么意思？谁再来说一说？

生：个位上的数字和十位上的数字合起来应是圆片的数量。

小结：个位上的数+十位上的数=圆片的数量。

在这一层次的探索操作中，首先通过4个圆片巩固有序地摆的方法，探索规律“圆片的个数+1=摆出的数的个数”。再通过直接有序写出5个圆片能摆出的数，探索“个位上的数+十位上的数=圆片的数量”。学生的思维从直观到抽象，从抽象到具体，向更高维度发展。

四、变式迁移，深化解题思维

片断四：结合情境，运用规律。

师：数学王国的国王，想和你们来一场比赛，你们敢不敢挑战？

1.运用有序思考。

师：城堡的密码是中间空着的这个数。你能马上破解吗？

2.运用发现的规律。

师：城堡里的三扇门分别对应国王的卧室、厨房、书房。门上分别有7、8、9个圆片和数位表，请选择你喜欢的一扇门写一写圆片表示的数有哪些。

结合具体情境，进一步加深学生对位值及各规律的理解。城堡的密码让学生体会有序思考的奥秘，写出不同圆片个数能表示的数，让学生对所学规律有进一步地认识。解题思维在分析和解决问题的过程中得到发展。

五、拓展延伸，激发创新思维

片断五：突破规律，拓展思维。

师：老师把这些数请到我们熟悉的百数图中，其实我们的智慧锦囊就藏在其中，你有发现吗？（课件依次涂色呈现）

师：如果给你们10个圆片，你们觉得可以创造出几个数？

师：到底是几个呢？小组合作，摆一摆、数一数、想一想。

师：请一位同学上来摆一摆，他边摆你们边报数我来记录。

师：10个圆片能不能都放在一格？

生：不能，因为一个数位上最多摆9个珠子。

师：所以一共摆出了几个？

生：9个数。

师：那11个呢？12个呢？13个呢？……我们课后再进行研究思考。

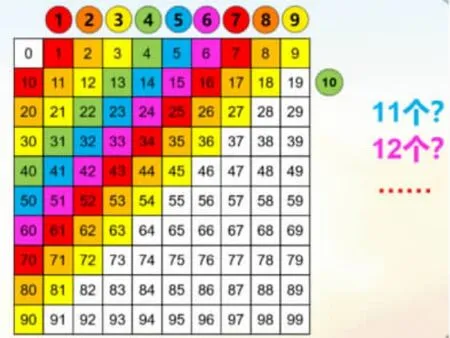
仍然是摆一摆问题，但圆片个数是10个及以上时不再满足“圆片的个数+1=摆出的数的个数”这一规律，摆出来的数相较9个圆片时反而变少了。这一奇特的现象再次激发学生的学习兴趣，不仅促使学生的思维在思辨中得以升华，更助力思维发散。11个、12个、更多的圆片又会怎样呢？课堂自然而然延续到了课外，数学研究回味无穷。