帮助学生探究“除法分配律”

文|胡海光 宋煜阳

学习乘法分配律时，学生会有“除法有分配律吗？”的疑问，可以借助以下活动，帮助学生经历对“除法分配律”的生疑、探疑、释疑的探究过程。

一、个例激疑，形成猜想

1.脱式计算，要求能简算的要简算。

（8+4）×25 15×（100+2）

（170+34）÷17 1200÷（20+30）

2.交流中形成“除法分配律”的猜想。

（1）根据前两题，回忆乘法分配律的字母表示方法：（a+b）×c=a×c+b×c，a×（b+c）=a×b+a×c。

（2）展示学生作品或课件演示。

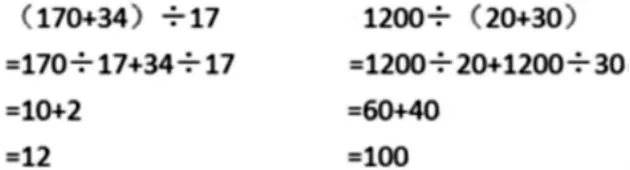
猜一猜：这两位同学这样做，他们是怎样想的？

（3）议一议，用字母表示两种猜想。

（a+b）÷c=a÷c+b÷c（c≠0）

a÷（b+c）=a÷b+a÷c（b≠0，c≠0，b+c≠0）

（4）讨论：除法有没有分配律？学生举例发现1200÷（20+30）≠1200÷20+1200÷30，明确“a÷（b+c）=a÷b+a÷c（b≠0，c≠0，b+c≠0）”不成立。

（5）质疑：“（a+b）÷c=a÷c+b÷c（c≠0）”成立吗？怎么验证？得出“列举类似的算式并通过计算来检验”“有没有反例”“举生活例子说明”等验证方法。

二、举例验证探疑，确认结论

1.提供《学习单》，学生举例验证。

2.全班交流。

（1）计算举例验证，引导寻找反例，确认结论成立。

（2）生活实例验证与画图验证，再次确认结论。

把66张纸平均分给3人，每人得到多少张？

66÷3=22

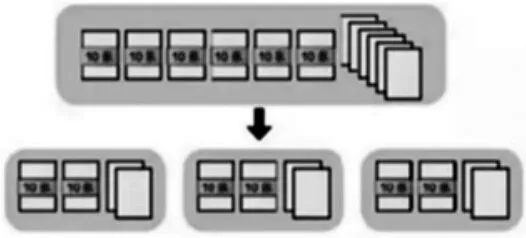
60÷3=20

6÷3=2

20+2=22

三、联系旧知释疑，引发二次猜想

1.回顾梳理：这个规律在以前的学习过程中遇到过吗？

回顾两位数除以一位数且商是两位数的口算过程。让学生举例说明（a+b）÷c=a÷c+b÷c（c≠0）的含义。

2.质疑：a÷（b+c）≠a÷b+a÷c（b≠0，c≠0，b+c≠0）为什么不能成立？用生活实例解释。

3.引发猜想：除了“两个数的和除以一个数”这种情况，还有哪些情况也会存在分配律？猜想多个数的和、两个数的差、两个数的积除以一个数是否存在分配律，用字母描述假定成立的规律。

四、再次组织学生探究，构成结论群

1.提供《学习单》，学生举例验证。

2.确认“多个数的和与两个数的差除以一个数”具有分配律。