简材厚学，发展思维

于飞 徐丹红

教学内容：

人教版数学四年级下册第72～73页。

课前思考：

四年级的“小数加减法”历来都被视为简单易学的内容，因为在该内容学习之前学生已经掌握了整数加减法、一位小数加减法、小数的意义和性质，已经有了一定的算理基础和迁移能力。事实也的确如此，通过前测（教材第72～73页“做一做”各选4题），发现数位相同的小数加减法（例1）正确率高达95%，而数位不同（例2）的正确率也有85%。那么面对这么高的正确率，如何让学生心目中的简单题目变得有趣，激发他们的学习热情呢？如何让大部分学生的“已会”内容变得有挑战、学有增量呢？基于以上学情和思考，本节课我们重组教材、沟通算理、变化形式，试图让看似简单的学习材料焕发生机，让学生学得更厚实，进而发展学生的运算思维。

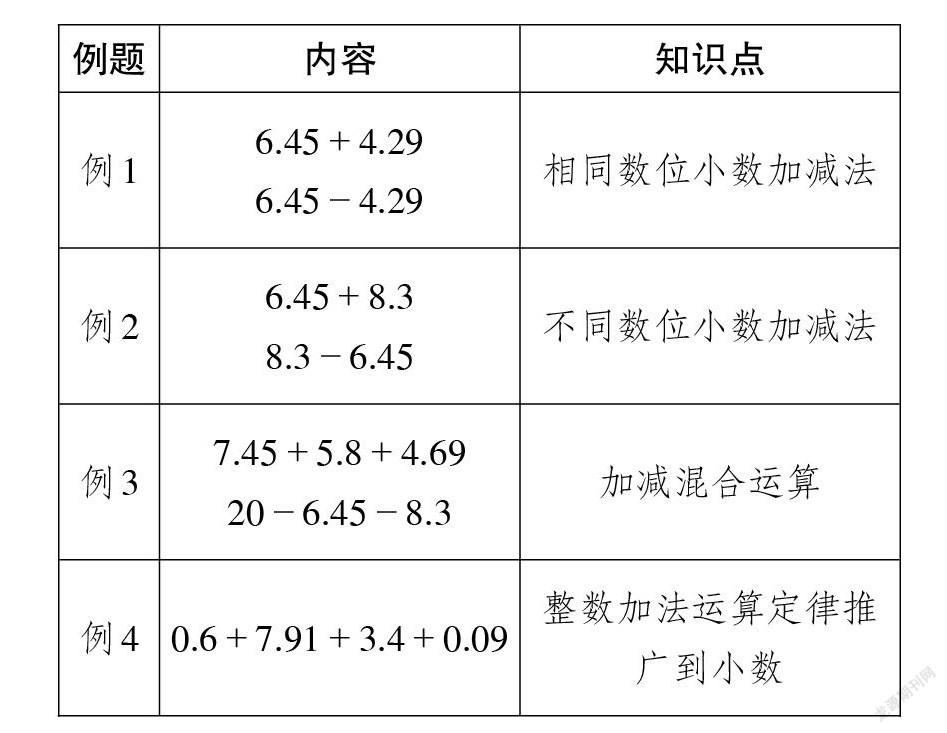
1.重组内容，融合口算和简算。依据学情，我们发现将例1作为教学的起点太低，而横向比较教材也证明了这一点。苏教版、冀教版、西南师大版和沪教版4个版本教材均直接从例2开始教学。因此，我们整合教材中的例1和例2，并以例2为主，同时渗透本单元后续例4的简便计算，再引入口算，让教学更加丰厚多元。

2.强化算理，沟通小数和整数。本课直入主题，从整数加减法切入，在正确和错误例子对比中，辨析、理解算理。同时沟通联系整数，寻找关联：无论是整数还是小数都是相同计数单位相加减。从而进一步强化算理。

3.变化形式，激发兴趣和提高能力。计算课要避免枯燥乏味，除了要深度理解算理，也要在练习形式上下功夫。本节课的练习设置了“创编习题，互做推荐”“挑战性练习，促进深度学习”“口算简算，灵活选择”3大类型习题，激发学生学习兴趣，提升运算能力。

教学过程：

一、直入主题，注重联系

师：今天我们学习加减法，你们脑海中想到了怎样的算式？

生：1+1=2，1+2=3，100+100=200……

师：有同学说到了整数加法，老师写一道（板书：854+63）。

（学生说笔算过程，教师板书竖式，教师添加小数点：8.54+6.3，揭示课题：小数加减法）

【思考】学生对小数加减法有很好的学情基础。教师没有过多铺垫，直接揭题，以学定教，同时蕴含整数和小数加减法的对比。

二、探究新知，沟通联系

1.竖式计算：8.54+6.3

学生独立竖式计算，教师寻找典型并板书在黑板上（如图1）。

2.对比正误，解释说理

（1）巧借估算，判断得数的合理性

师：哪个得数肯定不对？

生：方法①不对，因为8点几加6点几，不可能只有9点几，最少也有14。

师：是的，小数部分不看，8+6=14，实际比14还要大。看来估算可以帮助判断结果的合理性。

【思考】因为有了大量的整数加减法经验，学生做题正确率很高，只存在个别学生有方法①和方法②的错误。借助估算判断计算结果的合理性，体现了估算在笔算中的作用和价值，估算不是硬性要求才运用，而是源于题目的内在需求。

（2）追问缘由，深化算理理解

师：那6.3中的3要像整数那样与8.54中的4末尾对齐，还是与5对齐？

（大部分学生都支持3与5对齐）

师：为什么与5对齐？

生：因为计算时，十分位要和十分位对齐，百分位和百分位对齐。

师：你们的意思是相同数位要对齐。可为什么相同数位对齐了，就可以直接相加减了，背后的道理是什么？

（学生分小组讨论，交流汇报）

生：因为6.3中的3表示3个0.1，8.54中的5表示5个0.1，5个0.1加3个0.1就是8个0.1。

师：计数单位相同才能相加减。那方法②错在哪里？

生：它是4个0.01加了3个0.1，不是7个0.1。

师（小结）：原来相同数位对齐了，也就是计数单位相同了，才能直接相加减。

【思考】学生能想到相同数位要对齐，但这还不是真正的算理，因此在这里教师进一步深挖背后道理，及时追问。因为都表示几个0.1，计数单位相同，所以可以直接相加。

3.沟通联系，打通算法

师：观察对比这两道整数加法和小数加法题，你们有什么发现？

（学生小组讨论，交流汇报）

生：计算时都是相同数位对齐。整数部分是个位对个位，十位对十位，而小数部分是十分位对十分位，百分位对百分位。

师：是的。不管是整数部分，还是小数部分，都是相同数位对齐。还有其他发现吗？

生：虽然都是相同数位对齐，但整数是末尾对齐，而小数是小数点对齐。

（学生再说一说，教师圈画：整数竖式的个位，小数竖式的小数点）

师（小结）：在计算小数加法和整数加法时，都是相同计数单位上的数相加，只是整数加法是通过末尾对齐实现的，而小数加法是通过小数点对齐实现的。

【思考】小数加减法的教学，不应只局限于小数，而应该跳出小数，从整个加减法运算的维度看整数和小数的联系。在教学中教师引导学生观察发现：两者的算法算理是一样的，都是相同数位对齐，也就是计数单位相同才能相加減，只是在竖式对齐方式上略有区别。

4.竖式计算：8.54-6.3

师：小数加法会计算了，小数减法会计算吗？

（教师出示：8.54-6.3，学生独立计算，上台说计算过程）

师（小结）：在计算小数加减法和整数加减法时，都是相同数位对齐，计数单位相同才能相加减，而今天的笔算小数加减法是通过小数点对齐实现的。

三、变化形式，学有增量

1.创编习题，互做推荐

师：刚才都是老师出题，你们做题。现在改变形式，你们来出题。请看要求。

（1）每人创编1道小数加法题、1道小数减法题。题目可以制造点“小麻烦”，但小数位数不超过两位。

（2）同桌交换题目，互相做一做，并互相批改评价。

（3）四人小组讨论8道题，推荐最有价值的1道题，并上台说明理由。学生推荐如图2所示。

生：推荐1的理由：小数部分是连续的退位减法，我觉得很容易算错。

生：推荐2的理由：这道题也是连续退位的减法，但是整数减小数，我觉得整数后面添加两个0，计算起来更方便。

生：推荐3的理由：这道题是连续进位的加法，并且是向整数进1，得数2.00末尾的两个0去掉不影响大小。

（多个小组学生上台展示，说明推荐理由）

师：分享了这么多有价值的题目，现在你们能说说小数加减法的计算要点吗？

生：计算时一定要小数点对齐，然后按照整数的计算方法做题。

生：计算时要注意满十进1，如果不够减的话，要向前一位借1。

生：小数位数不同时可以末尾添0，变成小数位数相同，计算起来更方便。

【思考】学生创编习题，并且还要给同桌制造点“小麻烦”。出题的学生会认真思考，怎样的题目同桌可能会做错，而同桌在做题时会更加谨慎和认真，整个过程体现了数学思维的碰撞。最后学生上台推荐，有人说到进退位，有人说到小数的性质添0、去掉0，等等，都是非常有价值的分享。变传统的“通过练习展示学生错误”为“学生创编习题自发关注易错点”，这一过程不仅锻炼了学生的表达能力，也让注意要点的总结水到渠成了。

2.挑战练习，深度学习

课件出示：小马虎在计算“□+6.7”时，漏看了6.7的小数点，得到的和是70.35，正确的和是多少？

师：先想一想解题思路，再列式解答。

（学生独立解决问题）

师：不说算式，只说思考过程，谁来说？

生：因为漏看了小数点，所以现在的算式是“□+67=70.35”，先求出“□”里的数，求出来后，再加6.7就是正确的和了。

生：就是要先算出“□”里的数，然后再求出正确的和。

师：计算过程你们听懂了吗？现在谁来汇报算式？

生：70.35-67=3.35，3.35+6.7=10.05。

师（小结）：这一问题需要有序思考，还原求出方框里的数，然后算出正确的得数。

【思考】教学中，教师设计有挑战性的题目，能引发学生深入思考。教师有意要求：先不说算式，只说思考过程。考查学生能否清晰表达出自己的思考过程，让更多的学生听明白。这样的练习，不仅提升了学生运算思维能力，更培养了学生有序思考、清晰表达的综合能力。

3.口算简算，融合延伸

师：现在到了整节课注意力最集中的时刻。口算小达人，每题限定时间。

课件出示：3.08+1.2 6.8+2 7.45-0.5

6.3-3 1.76+4.8+0.24

（1）逐题闪现，写出得数。

（2）校对答案，评选优胜者。

师：哪些题目需要分享讲解？

（学生一致认为最后一题，题目很复杂）

师：1.76+4.8+0.24，计算起来真的很复杂吗？

生：哦！原来0.24与4.8交换位置，先算1.76+0.24=2，再算2+4.8=6.8。

（学生恍然大悟）

教师出示问题：小芳去文具店购买了下面四样文具，共花了多少元？

圆珠笔：2.36元/支 笔袋：12.8元/个

橡皮：1.2元/块 尺子：1.64元/把

学生独立尝试，大部分学生能根据数据特点进行简便计算。

师（小结）：在计算前，要先观察数据的特点，能简便的可以像整数那样简便计算。

【思考】教学中，教师利用限时计算、评比口算的形式，激发了学生的学习兴趣，提升了学生口算的速度。遇到最后一道题时，很多学生会发出感叹：太复杂了吧！但也有學生能迅速观察到数据特点，灵活计算。最后顺势出示解决问题的方法，简便方法的运用也就水到渠成了。融合口算简算，不仅调动了学生的学习积极性，也让学生感受到计算不需要拘泥于特定的形式，而是要关注数据，灵活选择计算方法。能口算就口算，口算难就笔算，有特殊数据可以简算。

【教学反思】

面对高起点的计算新授课，如何做到学有增量呢？

1.学生立场下的单元整体教学。高起点“高”在哪里？又该如何定位？我们不妨做前测：前测内容可以选取教材例题以及“做一做”的习题，也可以是自编的同类型的题目，真正把握学生的“高”与“低”。我们不妨做教材研究：可以横向对比不同教材，但更重要的是研究本教材的单元内容编排，了解单元的整体教学，把握单元的学习重、难点以及本内容在单元中的教学地位，有效整合，真正做到以学定教，学有所获。

2.核心算理下的运算思维的提升。学生会计算，不代表完全理解算理，也不代表在复杂背景下能灵活基于算理进行合理运算。因此，教师要精心设计算理探究环节，追问到算理最深处，切勿走过场。同时，围绕提升“运算能力”这一核心目标，设计多种形式的练习，充分调动学生的学习积极性，让学生在深化算理的同时学习算法。

（作者单位：浙江省海宁市南苑小学 浙江省海宁市教师进修学校）

投稿邮箱：405956706@qq.com