“童化”视域下的数学 可视化理解路径

林慧

童化即儿童化，是指基于儿童的立场，遵循儿童的身心发展规律，追寻儿童喜爱的趣味化状态的过程。“童化”数学学习，则是指从儿童的视角去观察和发现现实世界中的数学问题，用儿童的思维方式分析和解决数学问题，进而获得数学素养的全面提升和良好情感体验的过程。然而数学学科的抽象性容易造成儿童数学理解的困难和认知的障碍，伤害儿童数学学习的情感，如何基于儿童的需要，运用可视化方式助力儿童的数学学习呢？笔者进行了如下思考。

一、审视：当下学生数学学习的问题分析

《义务教育数学课程标准（2011年版）》（以下简称《标准》）指出：学生的数学学习应当是一个生动活泼的、主动的、富有个性的过程。然而审视当下的课堂，数学学习的“成人化倾向”和“过度化抽象”现象时有显现。

1.成人化倾向。儿童的认知水平、思维方式、情感世界等与成人不一样。教学中，教师常常从成人的视角设计教学，虽然关注知识和技能的掌握，但往往忽略了儿童的需要、儿童的学习方式等。尽管成人也曾经历过童年，然而随着不断成长，已经不能像儿童一样去感受和思考，变得更加理性和客观。在这样的背景下，数学学习少了童趣更少了儿童的主动参与，更多的是来自成人式思维的被动接受。例如，在“分数乘除法实际问题”的教学中，教师非常关注对题目中“单位‘1’”的分析，然而这也是学生理解的困难之处，不会找、找不对的现象比比皆是。为了帮助学生快速找出、找准“单位‘1’的量”，教师总结出“‘的’字前面”“‘比’字后面”是单位“1”的量的方法。这种程序性的方式，学生是很难理解的，割裂了数学学习与儿童思维之间的联系。在成人化的数学学习中，儿童缺少内驱力，更体会不到数学学习的快乐。

2.过度化抽象。儿童是数学学习的主体，儿童的成长与发展应是数学教学的根本目的。数学是抽象的，教师的思维和语言也是抽象的，因此儿童的数学学习需要大量的直观形象来帮助理解。然而我们的课堂常常受时间、场地、目标的窄化等因素的影响，忽视了直观形象的重要作用，忽视了直接经验的重要价值，忽视了儿童数学学习的过程。讲授代替了学生的体验，演示代替了学生的尝试，这样的过度化抽象违背了儿童认知发展的规律，让学生陷入数学学习的困境。

如何让数学教学真正地符合儿童的需求，符合儿童的认知发展规律呢？笔者提出了“童化的可视化数学学习”，让数学教学基于儿童、为了儿童。

二、释义：何为“童化”数学的可视化理解

1.“童化”概念的再厘清。童化即儿童化，是指基于儿童的立场，遵循儿童的身心发展规律，追寻儿童喜爱的趣味化状态的过程。“童化”数学学习，则是指数学学习中突出儿童的主体地位，从儿童的视角去观察和发现现实世界中的数学问题，用儿童的思维、方式分析和解决数学问题。

2.“可视化”内涵的深思考。“可视化”是指通过一定的方式让抽象、隐性的数学知识、数学问题、数学思维、数学理解显现出来。这里的“视”不仅指看得见，亦可指感受得到，即能用语言、文字、图画、肢体、想象等方式将数学描述出来，将数学思考的过程表达出来，让数学可感，从而促进学生获得数学素养的全面提升和良好的情感体验。

3.基于“童化”的数学可视化理解。从现有教学实践来看，“童化”的数学学习需要可视化的措施，可视化学习可以激发儿童的学习兴趣，有效地集中儿童的课堂注意力，更能帮助学生对抽象的数学知识产生具象化的理解。可视化学习让数学更直观。另一方面，可视化学习也能催生“童化”的创新表现，促进知识的理解和思维的深刻。比如，让儿童画数学，在描绘中让思维可见;让儿童说数学，在表达中让理解再现;让儿童做数学，在实践中让理解深刻。

總之，“童化”与可视化的联结，是一种符合儿童认知规律的学习方式。可视化数学学习可以激发儿童的学习动机，培养儿童问题解决、协作及创造等能力，实现学生数学素养的提升。

三、探寻：基于“童化”的数学可视化理解的路径

数学可视化有助于减轻儿童数学学习中因年龄、思维发展水平等因素造成的学习负担，真正为“童化”数学学习提供支持。笔者尝试从当下数学学习的问题根源出发，从以下几个方面实现数学的可视化理解。

1.问题情境——可视化理解的思维准备。《标准》中指出：数学教学要紧密联系学生的生活实际，从学生已有的知识出发，创设与学生生活环境、知识背景密切相关的，又是学生感兴趣的学习情境。这样的情境能够激发学生数学学习的积极性，诱发学生提出有价值的数学问题，并在问题的驱动下为进一步理解数学做好准备。

（1）童趣情境。在小学阶段，符合儿童年龄特点、富有童趣的数学学习情境深受学生的喜欢。例如，在“认识射线、直线和角”一课中，教师用拟人化的“小点点的运动”形式，让学生真切地感受到点动成线;在“三角形的练习课”中以卡通三角形带领大家畅游三角形乐园，学生在完成各项任务中主动巩固和建构出三角形知识的网络;在“圆的认识”一课中，教师以绘本《车轮为什么是圆的》为主线引发认知冲突，为学生后续学习打好了情感基础和思维基础。

（2）问题情境。学起于思，思源于疑，问题是引导学生思维的重要一环。教学中，教师应通过有效的问题设计或学生的自主提问激活学生的思维，为进一步学习做好准备。例如，在“认识射线、直线和角”一课中，教师再次以拟人化的问题“线段也想变成射线怎么办”引领学生思考，让“把线段的一端无限延长就得到了射线”这一概念自然地在点的运动中形成。教师再通过角色设定，提出“猜猜线段还会想些什么”的问题，引导学生自主提出“要是线段向两端无限延长呢”的问题，有效地实现了从“有限”到“无限”的突破，让“无限”看得见。

2.个体尝试——可视化理解的具身认知。情境的启发和问题的引领，需要儿童个体的尝试，就是每个儿童基于原有的知识经验对心得问题进行加工和理解。具身认知研究指出，当我们解释想法时，即使没有我们需要的词语，我们也倾向于画出形状，利用周围的空间来“传播”自己的想法。

（1）多元表征，在描绘中建构模型。在尝试解决问题的过程中，绝大多数儿童会基于自己已有的知识和经验，以及擅长的方式，如肢体、绘画、语言等来分析和思考。例如，在“列方程解决相遇问题”一课中，为了让学生更好地体会相遇问题的要素，教师可以请学生到前面来模拟两人从出发到相遇的行走过程，可以与同桌互相配合，用手指演示从出发到相遇的过程，在经历中体验相遇问题的“两人”“同时出发”“相向而行”等基本要素，可以用线段图表示出数量之间的关系，在演、画、列、说等多种表征中逐步抽象，体会方程模型思想。

（2）“童画”表达，在描述中形成结构。爱因斯坦曾经说过：“我的所有点子都是通过画图得来，语言只不过是我用来向别人解释想法的工具。”图和画更加贴合思维的特性，两者可以相辅相成、有机结合。在教学中，教师可以创造机会让学生画出心中的数学。如“画出你心中的0.3”“画出你心中的[34]”“画出你心中的‘-3’”等，学生在尝试用图画的表达中，对“数的概念”的理解和认知就会跃然纸上。

除了概念理解图，教师还可以通过绘制数学绘本、数学小报、思维导图等方式让学生的数学学习个性化地呈现出来。特别是思维导图，可以是一节课也可以是一个单元的内容，通过制作思维导图帮助儿童清晰地了解数学知识之间的关联与脉络，让关联看得见。因为小学生的年龄比较小，教师可通过“板书示范—尝试制作—展示评价”等系列活动，让学生学会用思维导图来表达数学的学习过程，在表达中建构个性化的认知结构。

3.合作交流——可视化理解的经验共生。尝试是一种个性化的思考，是个体思维的呈现，而合作能够让儿童看见自己的思考，看懂别人的思维，形成更全面的认识和理解。

例如，在“认识射线、直线和角”一课中，教师提出问题：“小点点想就这样朝着一个方向直直地一直跑一直跑，永远也不停下来，它会跑出什么图形呢？”让学生先閉上眼睛想一想，并追问：“能想出这个图形的样子了吗？”学生再动手画下这个图形，完成后进行展示、交流。

学生在个体的说明、集体的评议中优化出图形的样子，在争辩、说理和比较中，明确图形概念的特征。在可视化的思维对照中，促进经验的共生。

4.反思内省——可视化理解的个性建构。荷兰著名数学家和数学教育家费赖登塔尔教授曾指出：“反思是数学思维活动的核心和动力。”由此可见，反思不仅仅是对数学学习一般性的回顾或重复，更重要的是它指向学生数学思维活动的核心，在内省中实现个性化的建构。

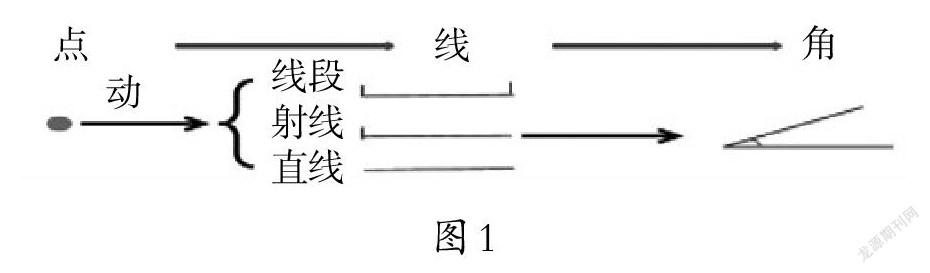
（1）借力可视化，实现童化育人。例如，在“认识射线、直线和角”一课的总结环节，如图1所示，学生通过自主回顾总结出本节课的知识要点，教师再通过课件的动态演示回顾学习过程，用“小点点的运动”这一童化情境，从图形运动的角度沟通了“点和线”“线段、射线和直线”之间的关系，感受数学的神奇。再通过“在线段、射线和直线中你最喜欢哪条线，能用它说一句话吗？”的问题让学生畅所欲言。“我喜欢线段，因为它有始有终，就像我们学习、做事一样。”“我最喜欢直线，因为它两端都可以无限延伸，无拘无束。”……最后教师送给大家三句话：“希望大家做事像线段，有始有终;学习像射线，学无止境;想象力像直线，想象无边创意无限。”在“说”与“送”中将线的特点化身为做人的道理，实现了童化育人的目标。

（2）借力可视化，实现学科育人。在课的总结阶段我们要善用可视化手段，引领学生回顾一节课学习的历程，形成学习的路径和方法，助力后续的学习，实现学科的育人价值。例如，在“小数的大小比较”一课中，教师通过动态呈现学习场景：“我提问—我思考—我尝试—我总结—我运用—我回顾”帮助学生在反思中形成探究新知的方法结构;还可以精心设计板书，在反思内省阶段，呈现出完整的知识结构，实现学科育人的价值。

综上所述，在“童化”立场的数学教学中，教师要重视数学可视化理解的重要价值，以直观可视的形式呈现数学的知识和过程，引领学生深入学习。因此，教师首先要关注问题情境的构建，为可视化理解做好思维的准备。其次要重视过程，让儿童在尝试与合作中表达，实现可视化理解的具身认知。最后要通过可视化理解的个性建构，实现数学学科的全面育人。

（作者单位：江苏省淮安市清河实验小学）