分段式叶片质量分布对风轮轴向窜动和陀螺效应的影响

李治国， 郝 波， 刘 乐， 高志鹰， 汪建文

(1. 内蒙古工业大学 机械工程学院， 呼和浩特 010051； 2. 内蒙古工业大学 能源与动力工程学院， 呼和浩特 010051；3. 内蒙古工业大学 风能太阳能利用技术教育部重点实验室， 呼和浩特 010051)

风力机在正常运行状态下，自然界湍流风与叶片相互作用会发生气弹耦合现象，叶片通常发生挥舞、摆振、扭转等振动变形[1-2]。然而柔性塔架使风轮沿主轴方向形成轴向窜动及旋转风轮对风时产生的陀螺效应，与通常所见叶片挥舞、摆振、扭转等变形具有显著区别[3-7]。由于这两种类型振动频率均低于风轮一、二阶振动，长期反复触发必然会加剧风轮的损伤程度，对风力机的安全稳定运行和使用寿命造成负面影响[8-13]。

Soleymani等[14]为减轻大型风力机风轮、塔架的振动传递，设计出一种混合无源/有源陀螺稳定器，来降低陀螺效应所产生的振动负能量。Da Costa等[15]利用有限元法研究一种添加襟翼复合结构的小型风力机，发现添加襟翼能够在一定程度上降低风轮的陀螺效应。Bahramiasl等[16]通过附加系泊链并试验测试海上风力机风轮振动变化，结果表明风轮轴向窜动会显著降低。Heg等[17]利用数学公式推导、物理机制，揭示轴向窜动和陀螺效应的影响因素，通过优化参数来降低这两种振动的影响。Hamdi等[18]运用有限元法研究发现，通过改变叶片刚度能够改善风轮陀螺效应。郭仁春[19]将超导磁悬浮轴承用于风力机，探究发现风轮陀螺效应、轴向窜动得到一定程度改善。迟凤东[20]运用数值模拟方法，研究风力机工作条件变化对风轮陀螺效应的影响程度，并通过改变陀螺力矩来降低风轮陀螺效应。

上述研究为降低风轮轴向窜动和陀螺效应提出多种方法，如加装陀螺稳定器、添加襟翼、附加系泊链、加装超导磁悬浮轴承等。本文基于分段式叶片设计理念[21-22]，以课题组自主设计S型水平轴风力机为研究对象，采用流固耦合数值模拟方法，结合内蒙古工业大学风能太阳能利用技术教育部重点实验室设备，探究两段式、三段式8种叶片质量分布对风轮轴向窜动及陀螺效应的影响，并提出最优质量分布方案。

1 数值计算

1.1 物理模型

在SolidWorks中建立如图1(a)水平轴风力机物理模型，叶片材料为木质，表面涂有玻璃钢材料，叶根处采用法兰连接；风轮轮毂中心距地面1.7 m，风轮直径为1.4 m。由于风力机大部分时间在额定工况下工作，所以主要选择额定工况进行数值模拟，因此选取额定风速、转速分别为8 m/s、545 r/min。图1(b)是风力机分段式叶片模型，依据风力机叶片分段原理，近似对不同位置进行单独密度设置，从而改变叶片质量分布并按长度比例1∶1和1∶1∶1进行分段。以内蒙古工业大学风洞实验室外形为基础，在ANSYS中建立如图2所示的风力机整机流场模型，入口截面距风力机旋转域平面为2D，出口距离风轮旋转平面为5D，D代表风轮直径。采用四面体网格对该流场进行划分，为了得到旋转域内准确的压力分布，对叶片及轮毂进行网格局部加密处理。

(a) 风力机整机模型

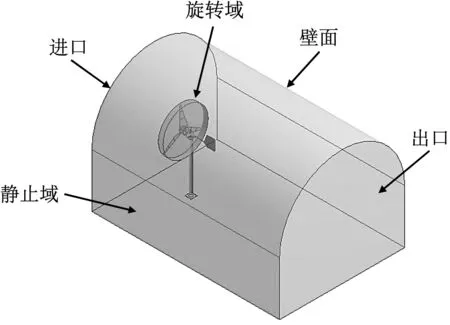
图2 风力机整机流场模型

1.2 边界条件设置

流体为25 ℃空气介质，入口边界条件为速度入口，大小为8 m/s；出口边界条件采用压力出口，相对压力为0；风轮旋转区域采用动网格技术实现流固耦合面上网格变形的传递，静止壁面采用无滑移条件，采用稳态计算，应用SST(Shear Stress Transport)方程进行求解。

1.3 风力机相关参数

对风力机进行模态数值分析时，材料参数设置的准确与否直接决定仿真结果的精确性。本文材料参数塔架密度为2 780 kg/m3，弹性模量为1.1×105MPa，泊松比为0.30；轮毂密度为7 250 kg/m3，弹性模量为1.13×105MPa，泊松比为0.25；轴段密度为2 950 kg/m3，弹性模量为2.0×105MPa，泊松比为0.30；叶片密度为625 kg/m3,弹性模量为4.8×103MPa；泊松比为0.33。针对实际风力机运行情况，对风力机塔架底部添加完全约束，即对风力机底部所有点进行完全约束。在额定工况下，导入前期流场计算获取的气动力载荷，添加风力机额定转速获取离心力。进而得到风力机风轮的动态响应，如振型、频率等。

1.4 气动力方程及其求解

气动力是气流流经叶片各个叶素面的微元力总和

(1)

(2)

式中:D为叶片表面阻力，N；L为叶片表面升力，N；Cd为阻力系数；CL为升力系数；ρ为空气密度，kg/m3；u为来流风速，m/s；c为叶片平均弦长，m；r为叶素微元距轮毂中心距离。

1.5 结构动力学运动方程

连续梁理论动力学方程

(3)

式中：ρ、E、I、S为单位体积叶片的质量、弹性模量、截面对中性轴的惯性积、叶片横截面积；f(x,t)为单位长度叶片上分布的外力；m(x,t)为单位长度叶片上分布的外力矩。

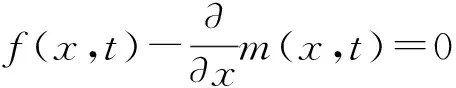
(4)

叶片的主振动可假设为

y(x,t)=φ(x)q(x)=φ(x)asin(ωt+θ)

(5)

代入自由振动方程

(EIφ″)″-ω2ρSφ=0

(6)

式中，ω为固有频率。

2 结果分析

2.1 原叶片(整段式)数值分析

通过数值模拟方法得到计算原叶片风轮轴向窜动频率为9.40 Hz，风轮陀螺效应频率为17.85 Hz，而风轮一阶对称、一阶反对称、二阶对称、二阶反对称均大于24.21 Hz。从频率数值来看风轮轴向窜动和陀螺效应远远小于风轮一、二阶固有频率，而从图3发现与刚性风轮相比轴向窜动沿轴向发生较大位移变化，塔架前后方向位移变化较为明显。风轮陀螺效应为平衡旋转力矩而产生涡动，从而与静止位置风轮发生一定错位现象。

(a) 原叶片风轮轴向窜动

2.1.1 试验验证

为验证原叶片风轮数值计算的可靠性，试验测试在内蒙古工业大学风能太阳能利用技术教育部重点实验室B1/K2式风洞开口试验段进行。对开路低速风洞开口段进行标定。风力机装配400 W永磁同步发电机，采用工况调节监测系统对风力机运行工况进行调节监测，在发电机前端紧靠风轮处布置加速度传感器捕获振动频谱，通过频谱分析法识别风轮运行模态。如图4振动信号分别由四个加速度传感器感知，布置位置分别为发电机顶部前端、发电机侧部前端、发电机顶端中部、发电机下端。利用谱分析法识别分段叶片风轮动频，加速度传感器感知测点处的振动信息，并由数据线传输给数据采集卡。数据采集卡收集数据，并对数据进行相关处理后，通过网线传输给电脑中的PULSE系统控制程序，控制程序完成测试系统的整体设置、控制及测试数据的显示。

(a) 试验设备原理示意图

2.1.2 可靠性分析

记录并整理试验数据得到表1，轴向窜动振动频率稳定在8.77 Hz，与数值模拟计算值9.40 Hz接近。陀螺效应振动频率稳定在17.14 Hz，与数值模拟计算值17.85 Hz接近。轴向窜动振动频率计算值与试验值相对误差控制在6.70%之内，陀螺效应触发频率计算值与试验值相对误差控制在3.98%之内。风轮在额定工况运行时，作用于风轮表面的轴向推力是导致风轮沿轴向往复运动原因之一，而塔架的弹性变形是发生轴向窜动另一个重要原因。因风轮旋转切向力方向时刻改变，从而使动量矩不断变化并使风轮产生陀螺效应。数值模拟的计算值与试验值存在差异，这是因为试验是通过布置于发电机前端部靠近风轮处的加速度传感器捕获频谱，这与数值计算理想的只针对风轮-塔架模型进行分析存在客观的差异性。但是最大误差仅有6.70%，证明该数值计算方法具有良好的可靠性，数值计算结构具有较高可信度。

表1 原叶片试验与模拟结果

2.2 两段式叶片轴向窜动

将叶片分割为两段式进行材料属性的计算，两段式叶片质量分布比例相对较为明显。从表2所示两段式叶片质量分布来看风轮轴向窜动易在低频时被触发且叶尖质量分布为30%、70%时频率数值分别为8.73 Hz、9.16 Hz。从图5风轮轴向窜动位移变化振型来看塔架发生位移变化相对较为明显。叶根质量分布为 30%时，塔架位移节点变化发生于塔架上段1/3处；叶根质量分布为70%时，塔架位移节点变化发生于塔架上段1/4处，由此分析可以发现叶尖质量分布变大对塔架位移影响范围逐渐扩大。轴向窜动致使三叶片沿轴向往复式运动，易在叶根处发生较大位移并承受较大往复式剪切应力。因此轴向窜动触发时易在叶片根部和发电机主轴产生疲劳损伤，而所带来的损伤累积会减少所在设计寿命周期内的正常运行概率。长期被触发必然会对叶片疲劳损伤产生严重影响，缩短叶片使用寿命。

表2 两段式叶片计算结果

(a) 叶根质量为30%

2.3 两段式叶片陀螺效应

由表2可以看出两段式叶片陀螺效应触发时，当叶根质量分布为30%时频率变化为24.59%；当叶根质量分布为70%时频率变化为5.15%。从频率数值变化来看叶根质量分布为30%时大于叶根质量分布为70%时。从图6可以看出三叶片振动形式相似，虽然振动顺序先后和幅度稍有差异，但同一时刻三叶片均处于刚性风轮两侧，图中平直不动的平面为风轮处于静止时的位置面。风轮旋转时产生旋转离心惯性力，导致叶根处承受回转式剪切应力。风轮切向力方向时刻发生改变，带来动量矩不断改变，近而造成陀螺效应频率变化的不同。陀螺效应振动频率数值变化相比于轴向窜动效应更为明显，因而可以得到叶片质量分布变化对陀螺效应有更大影响。

(a) 叶根质量为30%

2.4 三段式叶片轴向窜动

为近一步探究分段式叶片质量分布变化对风轮轴向窜动和陀螺效应的影响规律，将叶片分割为三段式进行研究。首先对三段式叶片轴向窜动进行探究，如表3所示三段式叶片质量分布情况及数据记录。当叶根质量分布为60%、叶尖质量分布为15%～25%时频率数值相比于原叶片降低7.57%～8.55%；当叶片中部质量分布为60%时频率数值相比于原叶片变化最大为18.14%。由以上数据可以看出，两段式叶片质量分布集中在叶尖可以降低风轮轴向窜动频率，而三段式叶片叶根质量大叶尖质量较小时可以降低频率数值。而从图7可以看出，质量分布1和3沿轴向发生窜动位移最大，塔架位移节点都发生于上段1/2位置处。质量分布2和4于60%集中叶片中部时，沿轴向窜动位移变化最小。而质量分布5和6轴向窜动位移变化介于上述两者之间。叶尖质量分布为60%时沿轴向窜动振动位移变化最大达15.38%，塔架位移影响范围变大，造成叶根部位和发电机主轴位移窜动剧烈。对于塔架设计时也应考虑沿轴向窜动振动的合理性。叶片中部集中质量分布为60%时对轴向窜动振动位移变化最小约3.45%。从频率变化来看，叶片质量60%集中于中部轴向窜动频率>叶片质量60%集中于叶尖轴向窜动频率>叶片质量60%集中于叶根轴向窜动频率。相比于频率数值变化，振动位移变化影响更加显著。这也说明风力机是个刚柔耦合的系统，而柔性叶片和塔架保证风力机安全稳定的运行。

表3 三段式叶片质量分布及结果

(a) 质量分布1

2.5 三段式叶片陀螺效应

从表3可以看出，叶尖质量分布为60%时频率数值相比于原叶片降低33.50%～35.40%；叶片中部质量分布为60%时频率数值相比于原叶片降低16.97%～28.74%。以上数据分析得出向叶尖集中质量时频率数值降低幅度相对较大，而陀螺效应相比于轴向窜动触发频率更大且相对于原叶片风轮频率数值变化极为显著。此类振动触发时所引起的位移变化量比轴向窜动更为明显，而此时风轮叶片振动形态与一阶对称振型形态有一定相似之处。风轮绕主轴不断回转，高速旋转的风轮动量矩不断改变方向。从叶根到叶尖的质量分布变化相当于改变叶片的质量矩阵，从而使旋转风轮切向力发生改变。两方面原因导致风轮在运行时触发陀螺效应。从以上分析看出叶片质量分布变化对陀螺效应有着显著影响。在实际工程应用中，保证叶片受力合理的前提下，适当改变叶片质量分布可有效改善风轮陀螺效应。

2.6 最佳选择方案

通过上述计算分析两段式叶片、三段式叶片的8种质量分布方案对2类典型振动影响。结果发现在保证叶片各个位置受力强度合理前提下，适当调整叶片质量分布，可有效降低风轮轴向窜动和陀螺效应。降低风轮轴向窜动最佳选择为6方案，从叶根到叶尖质量分布依次为60%、25%、15%。降低风轮陀螺效应最佳选择为1方案，从叶根到叶尖质量分布依次为15%、25%、60%。同时考虑风轮轴向窜动和陀螺效应最佳选择为5方案，从叶根到叶尖质量分布依次为60%、15%、25%，如表4所示。

表4 最佳方案

3 结 论

本文利用数值模拟方法及内蒙古工业大学风能太阳能利用技术教育部重点实验室设备，对拥有自主知识产权某S型叶片(整段式)的轴向窜动及陀螺效应进行对比分析，证实SST单向流固耦合数值模拟方法是准确可靠的。在此基础上，进一步探究两段式、三段式8种叶片质量分布对上述两种振动的影响，主要结论如下：

(1) 叶尖质量分布为60%对轴向窜动位移影响达15.38%，塔架位移变化范围扩大，加剧叶根部位和发电机主轴疲劳损伤。叶片中部质量分布为60%时对轴向窜动位移影响达3.45%，表明在保证叶片合理受力下可适当配置中部质量分布。

(2) 高速旋转的风轮动量矩不断改变方向，易在叶根处产生回转式剪切应力。三叶片同一时刻气动载荷不对称、质量分布不均匀使切向力时刻变化，叶尖质量为60%时对陀螺效应频率影响达33.50%以上。

(3) 降低轴向窜动最佳选择为质量分布6方案，降低陀螺效应频率最佳选择为质量分布1方案，同时考虑轴向窜动和陀螺效应最佳选择为质量分布5方案。

本文提出的最佳质量分布方案基于数值模拟方法，试验部分仅对原叶片(整段式)进行验证与可行性分析，后续研究工作将对分段式叶片进行实测。