实度与转动惯量对垂直轴风力机性能的耦合影响

王旱祥，马文龙，于洪栋，张金玲，姚明建，张立军



实度与转动惯量对垂直轴风力机性能的耦合影响

王旱祥，马文龙，于洪栋，张金玲，姚明建，张立军

(中国石油大学(华东) 机电工程学院，山东 青岛，266580)

当垂直轴风力机结构参数变化时，其实度和转动惯量均随之变化，进而耦合影响风力机性能。为此，以 200 W垂直轴风力机为研究对象，提出含转动惯量的CFD动态仿真模型，基于湍流模型实验确定使用RNG−湍流模型，分别对不同叶片数、风机半径、叶片弦长的垂直轴风力机进行仿真，通过垂直轴风力机启动时间判断其启动性能，采用运行时的最大风能利用率判断效率。研究结果表明：小转动惯量有助于减少风力机启动时间，提高启动性能；少叶片数、大半径、大叶片弦长有助于提高风力机稳定时的最大风能利用率，而风能利用率与实度、转动惯量没有明显关系。

垂直轴风力机(VAWT)；CFD仿真；实度；转动惯量

作为一种清洁的可再生能源，风能在中国具有极其丰富的储量。在国家政策措施推动下，我国风电产业进入稳定持续增长的新阶段[1-2]。垂直轴风力机凭借结构简单、无需对风、安装方便等优点，在零功耗公寓、城市公共照明等场合具有巨大的应用潜力[3-4]。但是，由于存在风能利用率低、启动能力弱等缺点，垂直轴风力机的规模化发展及应用受到限制[5]。实度是影响垂直轴风力机性能的重要设计参数[6]，对风轮的空气动力特性有较大影响。国内外学者开展相关研究探究实度对垂直轴风力机性能的影响规律。LI等[7-8]通过风洞试验测量不同叶片数的垂直轴风力机性能参数，发现风力机的风能利用率随着叶片数的增加而减小。QAMAR等[9]采用二维CFD技术仿真研究不同弦长和叶片数组合的非对称翼型NACA4312垂直轴风力机，确定实度与风力机运行叶尖速比范围的关系。SUBRAMANIAN 等[10]采用三维CFD技术仿真确定不同叶片数量的垂直轴风力机的风能利用率。通过上述国外学者的研究可知，CFD仿真技术与风洞实验手段均可有效探究实度对垂直轴风力机性能影响规律。此外，国内也有很多学者进行相关研究。张立勋等[11]通过样机实验及CFD技术研究风机半径、叶片弦长及数量对风力机性能的影响规律。张建新等[12]通过三维CFD技术研究不同风机半径、叶片弦长、叶片数及安装角度的垂直轴风力机，确定实度与风机启动性能之间的关系。丁国奇等[13]通过风洞实验研究叶片数量与风机半径组合的垂直轴风力机，测量不同参数组合下风力机的力矩与功率特性。上述文献大都是采用CFD仿真技术或风洞实验，通过软件设置或外加扭矩使得垂直轴风力机的转速保持恒定不变，然后测量相应叶尖速比下的风力机风能利用率，从而确定实度对风力机性能的影响。在现场工况下，风力机转速受到转动惯量和实度的耦合影响，处于波动状态。虽然上述研究方法能够确定实度对风力机的风能利用率及启动性能的影响规律，但忽略由实度变化引起的转动惯量变化对风力机相关性能的影响，导致相应的研究结果难以准确地反映实际工况。本文以RAINBIRD[14]在实验中采用的由静止到稳定转动的无负载垂直轴风力机为研究对象，提出一种含转动惯量的二维CFD动态仿真模型，并将不同湍流模型的仿真结果与实验结果对比，从而确定合适的仿真模型。利用该模型，研究由叶片数、叶片弦长及风机半径变化所引起的实度与转动惯量对垂直轴风力机性能的耦合影响效果，为进一步设计高风能利用率、优启动性能的垂直轴风力机提供 参考。

1 二维CFD动态仿真模型构建

在自然风作用下，垂直轴风力机叶片所受扭矩不断变化，其发电机的转速也随之变化[15]。而前人[9-12]的仿真模型假定风力机转速恒定，很难准确地反映垂直轴风力机的实际工作状态。因此，本文提出一种二维CFD动态仿真模型，并将其与文献仿真模型对比，如图1所示。

(a) 文献[9−12]中仿真模型；(b) 动态仿真模型

文献[9−12]的仿真模型中，垂直轴风力机转速恒定，通过求解N-S方程得到各叶尖速比下风力机性能。而本文仿真模型中，赋予风机以初始转速和转动惯量，根据N-S方程和动力学方程，确定每个时刻的风机运动及性能参数，更加准确地反映垂直轴风力机的真实工作状态。为详尽说明CFD动态仿真模型，以图2所示的RAINBIRD实验[14]中的200 W的H型垂直轴风力机为研究对象，列举动态仿真模型计算公式，垂直轴风力机的相关参数如表1所示。

首先，对特定时刻的垂直轴风力机的流场建立N-S方程。

连续性方程：

图2 H型垂直轴风力机示意图

表1 H型NACA0018垂直轴风力机相关参数[14]

动量方程：

图3 垂直轴风力机叶片1的受力示意图

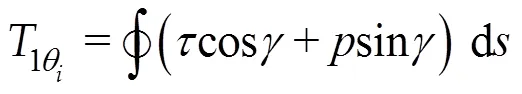
式中：为叶片数；为风力机叶片安装半径，m。

其次，根据刚体动力学知识，风力机的角加速度可由下式求得：

式中：为第时刻风力机的角加速度，rad/s2；为风力机的转动惯量，kg·m2。

通过四阶亚当斯−摩尔顿算法[16]迭代求解下一时刻风力机角速度+1：

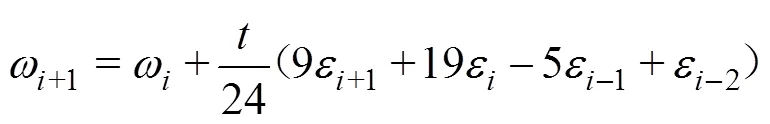
式中：为角速度，rad/s；为单步计算时长，s。

求得第时刻风力机对应的位置+1为

+1=++1(8)

待风力机角速度周期变化时，通过式(9)和式(10)求得风力机的平均功率ave和功率系数P：

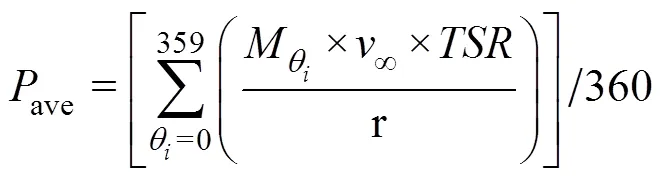
式中：s为风力机的扫略面积，m2；为风力机叶尖速比；∞为风速，m/s。

2 CFD仿真参数设置

因为垂直轴风力机叶片雷诺数低，存在严重的动态失速现象[17]，所以，目前关于准确仿真动态失速的CFD仿真参数仍无定论[18]。为保证CFD动态仿真模型的准确性，需要通过仿真试验确定合适的仿真参数，尤其是湍流模型。

首先，根据RAINBIRD实验条件，建立垂直轴风力机的二维仿真模型并确定边界条件，如图4所示。入口位于旋转中心上游4并设为来流速度6 m/s(其中，为风力机叶片半径)，出口位于旋转中心下游10.4并设为压力出口，计算域上、下两边相距7.2，并设为对称无滑移壁面边界，叶片和转轴的表面设为无滑移壁面边界，静域与旋转域采用滑移面连接。根据式(6)～(8)，编写旋转域运动udf程序。

其次，进行网格无关性验证。静域网格由外到内逐渐加密划分，网格加密区内叶片使用15个层边界，第1层单元高度为0.028 mm，增长率为1.2的边界层进行划分。计算域整体网格数为226 454个，节点数为152 073个，网格划分结果如图5所示。

图4 计算域及边界条件设置

图5 计算域整体网格

雷诺平均模型(RANS)在工业界广泛应用[19]，故采用RANS中的单方程S-A模型、RNG−模型、Realizable−模型、SST−模型和SST Transition模型分别进行仿真分析，结果如图6所示。

由图6(a)中不同湍流模型仿真结果可知，风力机叶尖速比从0增至稳定值，从而验证CFD动态仿真模型的可行性。为比较仿真结果与实验结果，将各时刻与启动稳定状态时刻进行比较，绘制−/曲线，得到图6(b)。以−/曲线变化趋势为仿真准确性评判标准，除S-A湍流模型以外，其他湍流模型仿真结果的增长趋势与实验结果相近。而就风力机稳定的叶尖速比而言，仅有Realizable−和RNG−湍流模型结果与实验结果相近，其他湍流模型所得值均大于试验值。故可知Realizable−和RNG−湍流模型均可保证仿真准确性。

为比较不同湍流模型的计算效率，针对不同湍流模型CFD仿真实验，使用MATLAB对相应−曲线采集数据，求解风机稳定时所需计算步数，结果如表2所示。RNG−湍流模型仿真达到稳定状态所需计算步数最少，而SST Transition湍流模型达到稳定状态所需计算步数最多，两者之间相差约2 707个计算步的耗时。综上所述，就风力机启动过程的二维CFD模型而言，相较于其他湍流模型，RNG−湍流模型计算不仅稳定时叶尖速比更接近于实验结果，而且达到稳定时的计算步数最少，故本文采用该湍流模型进行仿真分析。

(a) 不同湍流模型下叶尖速比λ−t曲线；(b) 不同湍流模型下叶尖速比λ−t/T曲线

表2 湍流模型实验仿真计算步数

3 实度与转动惯量对风力机性能的耦合影响

根据GB/T 13891—2009“小型风力机设计通用要求”，小型垂直轴风力机的叶片数量、弦长及风机半径是影响风力机性能的重要参数。而当上述任一参数发生变化时，垂直轴风力机的实度和转动惯量均将发生变化，故本文通过改变单一参数，控制其余任意2个参数不变，利用CFD动态仿真模型研究实度与转动惯量对风力机性能的耦合影响效果。其中，实度的计算公式如式(11)所示。而对垂直轴风力机的转动惯量进行简化处理，仅考虑风机叶片，通过SolidWorks的测量功能求得。

式中：为风力机实度；为风力机叶片数；为风力机叶片弦长，m；为风力机半径，m。

3.1 叶片数量

分别对3叶片、4叶片和5叶片垂直轴风力机进行仿真分析，计算叶尖速比及每一圈内风力机所受的平均扭矩，结果如图7所示。由图7中−关系曲线可知：在第1圈内，5叶片风力机的平均扭矩为0.5 N·m，大于3叶片、4叶片风力机所受扭矩。该现象出现的原因是此时风力机叶尖速比小于1，仍呈现出阻力型风力机特征[20]，故叶片数量越多，实度越大，风力机对于来流风场的阻碍作用越明显，使得扭矩增大。由图7中−关系曲线可知，3叶片风力机稳定波动的叶尖速比为3.9，启动时间为1.8 s，均优于4叶片、5叶片风力机相应参数。产生上述现象是因为随着叶片数量的增加，启动扭矩增加，但风力机转动惯量也增加，从而抑制扭矩增加对于风力机启动的积极作用，减缓风力机的加速过程，降低稳定时的叶尖速比。因此，随着叶片数量增长，风机的实度和转动惯量增大，在二者的耦合影响下，风力机启动扭矩提高，但是风力机到启动时间也增大。

实线：叶尖速比；虚线：平均扭矩

为分析叶片数对风能利用率的影响，根据叶尖速比稳定时的数据，计算得到不同叶片数风力机的p−关系图，如图8所示。3叶片风力机的瞬时风能利用率峰值为0.38，远高于其他叶片数风力机相应参数。产生上述现象是因为在风力机处于叶尖速比稳定波动时，叶片数越多，实度越大，对来流风场的阻碍作用越大，使得风能利用率降低。综上所述，3叶片垂直轴风力机启动性能最优，叶尖速比稳定时的风能利用率最高。

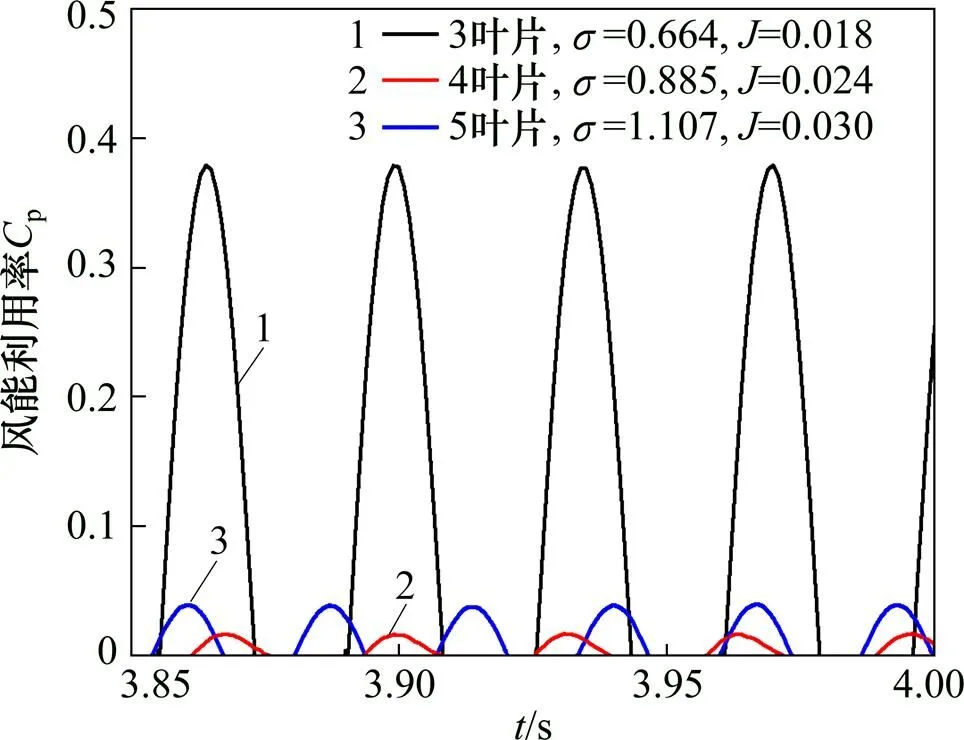
图8 稳定状态下不同叶片数风力机风能利用率−时间的关系

3.2 风机半径

分别对0.5倍、1.0倍及2.0倍半径的垂直轴风力机进行仿真分析，计算得到叶尖速比及每一圈内风力机所受的平均扭矩，如图9所示。由图9中−关系曲线可知：在任一圈内，当风机半径增加时，风力机所受的平均扭矩随之增加。结合式(5)可知，风力机所受扭矩由推力、风机半径决定。故为了分析上述现象的原因，提取推力实时数据，绘制不同半径风力机的−关系图，如图10所示。从图10可见：不同半径垂直轴风力机处于加速阶段时，所受推力先振荡上升至峰值，后振荡下降；处于稳定阶段时，所受推力在0 N·m附近以不同幅度振荡；在加速阶段，2.0倍半径垂直轴风力机所受的最大推力为7.2 N·m；在稳定阶段，其所受最大推力为2.4 N·m，均大于其他半径值对应的风力机所受推力值。因此，2.0倍半径垂直轴风力机所受扭矩最大。

由图9中−关系曲线可知：2.0倍半径风力机启动时间最长，为2.2 s；而0.5倍风力机启动时间则最短，为1.6 s，启动性能最优。这是因为当风力机半径增加时，风力机所受扭矩随之增加，转动惯量也随之增加，抑制扭矩增加对风力机启动的积极作用，减缓风力机加速过程。因此，随着风机半径增长，风机实度减小，而转动惯量增大，在二者耦合影响下，虽然风力机启动扭矩提高，但是启动时间增大。

实线：叶尖速比；虚线：平均扭矩

图10 不同半径风力机推力−时间的关系

为分析风机半径对于风能利用率的影响，根据叶尖速比稳定时的数据，计算得到不同半径风力机的p−关系图，如图11所示。从图11可见：2.0倍半径的风力机风能利用率峰值达0.58，远高于其他半径值对应的风力机。为解释上述现象，取转速稳定时不同半径风力机的涡量图，如图12所示。由图12可知：0.5倍半径风力机实度较大，叶片尾流涡量大于50 s−1，严重影响其他叶片的流场，而2.0倍半径风力机实度较小，叶片尾流涡量则较小，对其他叶片的流场影响小，从而使得大半径、小实度垂直轴风力机的风能利用率更高。综上所述，0.5倍半径垂直轴风力机的启动性能最优，而2.0倍半径垂直轴风力机的风能利用率最高。

3.3 叶片弦长

分别对0.5倍、1.0倍及2.0倍弦长的垂直轴风力机进行仿真分析，计算得到叶尖速比及每一圈内风力机所受的平均扭矩，如图13所示。由图13中−关系曲线可知：在任一圈内，当叶片弦长增加时，风力机所受的平均扭矩增加。产生该现象的原因是风力机在同等转速下，当叶片弦长增加时，叶片周围雷诺数随之增加，而根据美国SANDIA实验报告[21]可知，叶片升力系数也会随之增加，因此，2.0倍弦长风力机叶片升力最大，所受扭矩最大。由图13中−关系曲线可知：2.0倍弦长风力机启动时间最长，约为4 s，而0.5倍弦长风力机启动时间最短，为1 s，启动性能最优。该现象与不同风机半径相应现象发生原因相同，均因为风力机参数变化导致转动惯量增加，减缓风力机的加速过程。因此，随着叶片弦长增长，风机实度和转动惯量随之增大，在二者耦合影响下，风力机启动扭矩提高，但风力机启动时间增大。

图11 稳定状态下不同半径风力机风能利用率−时间的关系

(a) 0.5倍半径；(b) 1.0倍半径；(c) 2.0倍半径

实线：叶尖速比；虚线：平均扭矩

为分析叶片弦长对于风力机风能利用率的影响，根据叶尖速比稳定时的数据，计算得到不同叶片弦长的风力机p−关系图，如图14所示。从图14可见：2.0倍弦长风力机的风能利用率峰值为0.4，原弦长风力机风能利用率峰值为0.38，二者接近，而0.5倍弦长风力机的风能利用率峰值约为0.23。为解释上述现象，取转速稳定时不同半径风力机的涡量图，如图15所示。对比图12(a)和图15(c)可知：虽然0.5倍半径和2.0倍弦长风力机实度相同且均为1.328，但是2.0倍弦长的风力机叶片的失速现象较轻，涡量也小。这说明即使实度相同，不同结构参数的变化对风机流场影响不同，如大弦长叶片使得雷诺数升高，叶片升力提高，层流分离现象缓解，而小半径风力机则不会产生上述现象。由图15可知：在不同弦长风力机中，2.0倍弦长风力机失速现象最为严重，但其叶片雷诺数的升高促进升力提高，从而使得其风能利用率最高。综上所述，0.5倍弦长垂直轴风力机的启动性能最优，2.0倍弦长垂直轴风力机的风能利用率最高。

图14 稳定状态下不同叶片弦长风力机风能利用率-时间的关系

(a) 0.5倍弦长；(b) 1.0倍弦长；(c) 2.0倍弦长

4 结论

1) 叶片数量增加时，实度增加，转动惯量增加，风力机启动时间增加，且稳定时的最大风能利用率降低；3叶片风力机性能最优。

2) 风力机半径增加时，实度减小，转动惯量增加，风力机启动时间增加，而稳定时的最大风能利用率增加；0.5倍半径风力机的启动性能最优，而2.0倍半径风力机的风能利用率最高。

3) 叶片弦长增加时，实度增加，转动惯量增加，风力机启动时间增加，而稳定时的最大风能利用率增加；0.5倍弦长风力机的启动性能最优，2.0倍弦长风力机的风能利用率最高。

4) 小转动惯量有助于提高垂直轴风力机的启动性能，而实度、转动惯量与风力机稳定运行时的风能利用率没有明显关系。

[1] 李岩. 垂直轴风力机技术讲座(六) 垂直轴风力机应用及其发展前景[J]. 可再生能源, 2009, 27(6): 118−120. LI Yan. Lecture on the technology of VERTICAL-AXIS (VI) (the end) application and development prospect of vertical axis wind turbine [J]. Renewable Energy Resources, 2009, 27(6): 118−120.

[2] 张立军, 马东辰, 赵昕辉, 等. 小型H型垂直轴风力机变桨机构的优化设计与试验[J]. 西安交通大学学报, 2018, 52(3): 132−138. ZHANG Lijun, MA Dongchen, ZHAO Xinhui, et al. Optimal design of pitch mechanism for H-type vertical axis wind turbine[J]. Journal of Xi’an Jiaotong University, 2018, 52(3): 132−138.

[3] 张立军, 赵昕辉, 王旱祥, 等. H型垂直轴风力机实时高效攻角调节方法研究[J]. 机械工程学报, 2018, 54(10): 173−181. ZHANG Lijun, ZHAO Xinhui, WANG Hanxiang, et al. Study on the real time and efficient adjustment law for H-type vertical axis wind turbine[J]. Journal of Mechanical Engineering, 2018, 54(10): 173−181.

[4] LEUNG D Y C, YANG Yuan. Wind energy development and its environmental impact: a review[J]. Renewable & Sustainable Energy Reviews, 2012, 16(1): 1031−1039.

[5] BHUTTA M M A, HAYAT N, FAROOQ A U, et al. Vertical axis wind turbine: a review of various configurations and design techniques[J]. Renewable & Sustainable Energy Reviews, 2012, 16(4): 1926−1939.

[6] 杨益飞, 潘伟, 朱熀秋. 垂直轴风力发电机技术综述及研究进展[J]. 中国机械工程, 2013, 24(5): 703−709. YANG Yifeng, PAN Wei, ZHU Huangqiu. Review and research progress of vertical axis wind turbine[J]. China Mechanical Engineering, 2013, 24(5): 703−709.

[7] LI Qing’an, MAEDA T, KAMADA Y, et al. Effect of number of blades on aerodynamic forces on a straight-bladed vertical axis wind turbine[J]. Energy, 2015, 90: 784−795.

[8] LI Qing’an, MAEDA T, KAMADA Y, et al. Effect of solidity on aerodynamic forces around straight-bladed vertical axis wind turbine by wind tunnel experiments (depending on number of blades)[J]. Renewable Energy, 2016, 96: 928−939.

[9] QAMAR S B, JANAJREH I. A comprehensive analysis of solidity for cambered darrieus VAWTs[J]. International Journal of Hydrogen Energy, 2017, 42(30): 19420−19431.

[10] SUBRAMANIAN A, YOGESH S A, SIVANANDAN H, et al. Effect of airfoil and solidity on performance of small scale vertical axiswind turbine using three dimensional CFD model[J]. Energy, 2017, 133: 179−190.

[11] 张立勋, 梁迎彬, 李二肖, 等. 实度对直叶片垂直轴风力机风轮气动性能的影响分析[J]. 农业机械学报, 2013, 44(5): 169−174. ZHANG Lixun, LIANG Yingbin, LI Erxiao. et al. Effects analysis of solidity on aerodynamic performance of straight- bladed vertical axis wind turbine[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(5): 169−174.

[12] 张建新, 蔡新, 潘盼. H型垂直轴风力机启动性能分析[J]. 水电能源科学, 2013, 31(5): 243−246. ZHANG Jianxin, CAI Xin, PAN Pan. Analysis of start-up performance on H-shaped vertical-axis wind turbine[J]. Water Resource and Power, 2013, 31(5): 243−246.

[13] 丁国奇, 李岩, 王绍龙, 等. 实度对垂直轴风力机性能影响的风洞试验[J]. 可再生能源, 2013, 31(9): 58−62. DING Guoqi, LI Yan, WANG Shaolong, et al. Wind tunnel test on effects of solidity on performance of vertical axis wind turbine[J]. Renewable Energy Resources, 2013, 31(9): 58−62.

[14] RAINBIRD J．The aerodynamic development of a vertical axis wind turbine[D]. England: Durham University, School of Engineering, 2007: 78−80.

[15] MAHDI T A, ERFAN Z N, FAIZAL M, et al．Study on start-up characteristics of H-Darrieus vertical axis wind turbines comprising NACA 4-digit series blade airfoils[J]. Energy, 2016, 112: 528−537.

[16] WILCOX D C. Turbulence modeling for CFD[M]. La Canada CA: DCW Industries Inc, 1998: 76−80.

[17] 帕拉斯基沃尤. 垂直轴风力机原理与设计[M]. 李春, 叶舟, 高伟, 等. 上海: 上海科学技术出版社, 2013: 45−50. PARASCHIVOIU I. Principle and design of vertical axis wind turbine [M]. LI Chun, YE Zhou, GAO Wei, et al. Shanghai: Shanghai Science and Technology Press, 2013: 45−50.

[18] WANG Shengyi, INGHAM D B, MA Lin, et al. Turbulence modeling of deep dynamic stall at relatively low reynolds number[J]. Journal of Fluids & Structures, 2012, 33(5): 191−209.

[19] SANDERSE B, VAN DER PIJL S P, KOREN B. Review of computational fluid dynamics for wind turbine wake aerodynamics[J]. Wind Energy, 2011, 14(7): 799−819.

[20] HILL N, DOMINY R, INGRAM G, et al. Darrieus turbines: The physics of self-starting[J]. Proceedings of the Institution of Mechanical Engineers Part A Journal of Power & Energy, 2009, 223(1): 21−29.

[21] SHELDAHL R E. Aerodynamic characteristics of seven airfoil sections through 180 degrees angle of attack for use in aerodynamic analysis of vertical axis wind turbines[R]. Albuquerque, America: Sandia National Laboration, SAND80-2114, 1981: 20−25.

Coupling effect of solidity and moment of inertia on performance of vertical axis wind turbine

WANG Hanxiang, MA Wenlong, YU Hongdong, ZHANG Jinling, YAO Mingjian, ZHANG Lijun

(College of Electromechanical Engineering, China University of Petroleum, Qingdao 266580, China)

The solidity and moment of inertia of wind turbine change with the configuration parameters of vertical axis wind turbine(VAWT), which influence the performance of VAWT. Based on 200 W VAWT, CFD dynamic simulation model including moment of inertia was proposed. Through comparing simulation results obtained from different turbulence models, RNG−was proposed. Through CFD dynamic simulation model, wind turbines of different number of blades, turbine radius and blade chord were simulated. Length of start-up time and maximum coefficient of power were respectively used to evaluate starting performance and efficiency. The results show that small moment of inertia reduces start-up time of wind turbine and improves starting performance. The small number of blades, large radius, and large blade chord length contribute to the improvement of efficiency, but there is no obvious relationship between solidity, moment of inertia and maximum wind turbine efficiency.

vertical axis wind turbine (VAWT); CFD simulation; solidity; moment of inertia

KT 83

A

1672−7207(2019)05−1244−08

10.11817/j.issn.1672−7207.2019.05.029

2018−07−27；

2018−11−30

国家自然科学基金资助项目(51707204)；中央高校基本科研业务专项资助项目(17CX05021)(Project (51707204) supported by the National Natural Science Foundation of China; Project(17CX05021) supported by the Fundamental Research Funds for the Central Universities)

张立军，博士，教授，硕士生导师，从事可再生能源技术和绿色装备制造研究；E-mail：zhanglijun@upc.edu.cn

(编辑 秦明阳)