套筒结构对双层套筒式控制阀气动噪声的影响分析

钱锦远， 于龙杰， 侯聪伟， 蒋永兵， 郝娇山， 王伟波， 金志江

(1. 浙江大学 能源工程学院化工机械研究所, 杭州 310027； 2. 重庆川仪调节阀有限公司, 重庆 400707)

气动噪声是一种由气流直接产生，且频率杂乱、统计上无规律可循的声音。当人体长期处于气动噪声环境中，其听力会遭受较大的损伤，并容易产生负面情绪。控制阀内结构复杂，当高速气流流经控制阀内部结构时，压力迅速降低发生超声速流动，导致气体湍流程度快速增大并产生较大噪声，对现场操作人员的身心健康以及管路设备的安全运行有着严重影响[1]。多孔套筒又被称为笼式套筒或多孔笼罩，由于其多孔结构，有助于控制阀降低噪声，减小振动，被广泛应用于控制阀内部结构，提高阀门寿命[2]。将单层套筒改进为双层套筒，可进一步提升该控制阀的降噪性能。

许多学者对控制阀噪声与降噪措施做了大量的研究。Fan等[3]总结了控制阀的噪声预测方法以及噪声抑制的一般措施，主要包括采用迷宫式阻性消声器和多级套筒阀芯。Wei等[4]通过数值模拟法，发现在出口空腔中设置带孔节流板可有效地降低流致噪声。Berestovitskiy等[5]通过试验研究了带孔节流元件对调节阀流致噪声的抑制作用。但是，有研究表明节流元件会增大调节阀的气动损失，降低其流通能力[6]。此外，Youn等[7]发现径向狭缝结构对减压阀的高频噪声有较大的抑制作用，并且试验验证了降噪的有效性。张田等[8]采用鼓形出口和内壁小孔的结构对锅炉给水泵最小流量循环阀的出口进行改造，经分析该结构具有较好地抑制噪声效果。王佳典等[9]基于计算流体力学(computation fluid dynamic, CFD)和声学计算法，对某一种控制阀的管路流体噪声进行了瞬态方法和准稳态方法的对比分析，比较了计算精度与计算量的优缺点。孙长周等[10]通过声比拟法计算并提取阀内壁声压，并通过声振模型求解了阀门外部声场。苏华山等[11]基于Fluent软件以及动网格技术，发现流量的波动是导致阀芯产生振动噪声的主要原因。刘翠伟等[12]采用CFD软件耦合专业声学软件方法对气体流经阀门的气动噪声进行了研究，并确定流场中强烈的压力、速度脉动是阀门气动噪声产生的根本原因。Ryu等[13]利用频域声学模拟计算节流阀的内部气动噪声。此外，高温蒸汽等介质还涉及传热过程对噪声的影响，Qian等[14]发现较低的管壁温度不仅能强化对流换热，还可起到减弱气动噪声的效果。

噪声是控制阀最重要的性能指标之一，但是目前缺少针对套筒结构参数对控制阀噪声影响的相关研究，尤其针对双层套筒式结构。双层套筒式结构控制阀简称为双层套筒式控制阀。本文对双层套筒式控制阀建立不同套筒间距和套筒厚度数值模型，并对其模拟结果进行比较。本文的研究成果对于套筒式控制阀套筒结构设计具有重要的参考意义。

1 计算模型与控制方程

1.1 控制方程

过热蒸汽流经控制阀时满足可压缩气体流动方程，包括连续方程、动量方程与能量方程。此外，控制阀气动噪声模拟还涉及到宽频噪声模型与声学类比模型。在实际工程问题中的湍流噪声并没有明显的音调，它的频率范围连续分布在一个宽频段范围内，我们称为宽频噪声。目前有许多宽频噪声半经验修正模型，包括Proudman方程模型、线性Euler方程源项模型、Lilley方程源项模型等，其中Proudman方程模型是使用最为广泛的一种。基于Lighthill声类比模型，Proudman推导出了无均流各向同性湍流的声功率公式。考虑延迟时间差，Lilly重新推导了Proudman方程，其描述了单位体积各向同性湍流派生出的声功率PA，如式(1)所示

(1)

式中：u为湍流流速；l为特征长度；c为声速；α为模型常数。声功率级(acoustic power level)使用式(2)计算得到

(2)

式中，基准声功率Pref为1×10-12W/m3。

Ffowcs Williams and Hawkings方程(FW-H 方程)采用最通用的Lighthill的“噪声类比”方法，可以求解由单极子、偶极子和四极子产生的噪声传播。ANSYS Fluent采用时域积分的方法，通过少量的面积分计算指定位置的噪声。ANSYS Fluent中基于“可穿透面积分”的FW-H模型可以很好解决高、亚速气动噪声问题。声压级时域信号可以通过快速傅里叶变换(fast Fourier transform, FFT)，结合后处理，获得监测点总声压级、声压级频域信息和功率谱。FW-H方程是基于连续性方程以及N-S方程得出的非均匀波动方程，如式(3)所示

(3)

式中：ui为xi方向上的流体速度分量；un为垂直于f=0面的流体速度分量；vi为xi方向上的表面速度分量；vn为垂直于f= 0面的表面速度分量；δ(f)为狄拉克δ函数；H(f)为亥维赛函数；p′为远场声压(p=P-P0)；f= 0被视为声源面；a0为远场声速；Tij和Pij分别表示Lighthill应力张量和压应力张量。

1.2 几何模型

本文研究采用的双层套筒式控制阀模型，其流量特性曲线为可调比50∶1的等百分比流量特性。其结构示意图如图1所示。内外层小孔分布方式相同，外层小孔孔径为内层小孔孔径的1.2倍。小孔在套筒的排布方式遵循“下疏上密，下小上大”的原则，越底层的小孔又小又疏，越顶层的小孔又大又密。

图1 双层套筒式控制阀结构示意图

不同套筒间距和不同套筒厚度下双层套筒结构示意图，如图2所示。不同套筒间距和套筒厚度模型参数，如表1所示。由图2和表1可知，将套筒最小厚度设置为2 mm，最小间距为1 mm。以内层套筒内侧壁面为基准(内层套筒内层壁面直径等于阀塞直径，37.5 mm)，向外改变套筒结构。套筒间距设置为1 mm，3 mm，5 mm和7 mm，套筒厚度设置为2 mm，3 mm，4 mm和5 mm。

(a) 2-1-2

表1 不同套筒间距和套筒厚度模型参数

1.3 网格划分

本文采用十二面体网格对流道模型进行网格划分。由于多孔流道的结构复杂，不适合采用结构网格，因此选用非结构网格对流道进行划分。与四面体网格相比，十二面体网格的数量和计算时间更少，但计算精度较高，收敛性更好。以最大单元面网格尺寸为自变量划分网格，再观察模拟结果中出口流量变化，完成网格独立性验证。最大面网格尺寸小于等于2.5 mm时，出口流量基本不变，因此将面网格最大尺寸设置为2.5 mm，用来划分流道模型网格，如表2所示。流道模型网格，如图3所示。

表2 网格独立性验证

图3 流道模型网格示意图

1.4 边界条件及设置

控制阀内部流体介质为380 ℃(653 K)过热蒸汽，其物性参数如表3所示。将入口压力和出口压力分别设置为10.75 MPa和2.5 MPa。由于控制阀内部介质流动时，温度发生波动，导致密度变化，因此将介质密度设置为理想气体(ideal-gas)。由于涉及可压缩流体，采用密度基求解器及稳态求解。

表3 380 ℃过热蒸汽物性参数

在控制阀稳态流场的基础上，对控制阀流场进行宽频噪声模拟。当计算控制阀稳态流场模拟完成以后，开启宽频噪声源模型(Broadband Noise Sources)选项。对控制阀流场外部监测点进行声类比模型研究时，需要借助控制阀稳态流场模拟结果作为瞬态流场模拟的初始条件，这样可以使初始条件更接近真实状态，瞬态流场模拟结果更准确。开启Ffowcs Williams and Hawkings方程模型选项，再设置噪声源(Define Sources)，将壁面(wall)均设置为噪声源。根据GB/T 17213.8—2015《工业过程控制阀 第8-1部分：噪声的考虑 实验室内测量空气动力流流经控制阀产生的噪声》中的规定，设置控制阀外侧监测点，如图4所示。设置完上述参数后，还需在求解方法中进行调整。将Formulation设置为显式(Explicit)，将Transient Formulation设置成二阶隐式(second order implicit)，其他参数均不改变。最后，需要对时间步长(time step size)以及时间步数(number of time steps)进行设置。时间步长决定了声学分析中最高频率的大小。由文献调研可知，目前控制阀噪声频谱分析中最高频率基本位于5 000～8 000 Hz。本文的分析将最高频率fc设置为8 000 Hz，对应的采样频率fs为16 000 Hz，计算得到时间步长为6.25×10-5s。考虑到每个case的计算时长以及case数量，在确保采样信号的数量足以还原原信号的基础上，将计算总时长设定为0.1 s，时间步数设置为1 600。

图4 双层套筒式控制阀测点布置示意图

2 计算与分析

2.1 数值结果验证

由于缺乏相关噪声测试的试验条件，无法对文中的噪声模拟结果的有效性直接进行试验验证，因此只能借助有关学者的噪声研究成果来间接证明本文数值模拟方法的可行性。娄燕鹏[15]对高压降多级降压疏水阀及阀控管道的振动噪声特性进行了研究。其研究对象也为多级套筒式控制阀，口径为DN100，入口压力为5.9 MPa，出口压力为1.9 MPa，介质为200 ℃的高温水。对疏水阀进行噪声研究时，其最高采样频率与本文相似，均为8 000 Hz；对疏水阀噪声监测点的设置，其与本文相似，同样参考了标准GB/T17213.8—2015。疏水阀噪声研究中，监测点202与本文中监测点1位置相同，相互对应。选取了本文中较为典型的2-3-2模型小开度时监测点1的频谱特性曲线，与疏水阀监测点202的频谱特性曲线进行对比，发现两者的频谱特性曲线规律基本一致，如图5所示。噪声主要频率范围位于0～2 000 Hz，声压级均小于100 dB；随着频率的增大，声压级逐渐降低；当频率大于5 000 Hz时，声压级趋于稳定状态。这一结果也间接证明了本文基于数值模拟方法得到的模拟结果的可靠性。

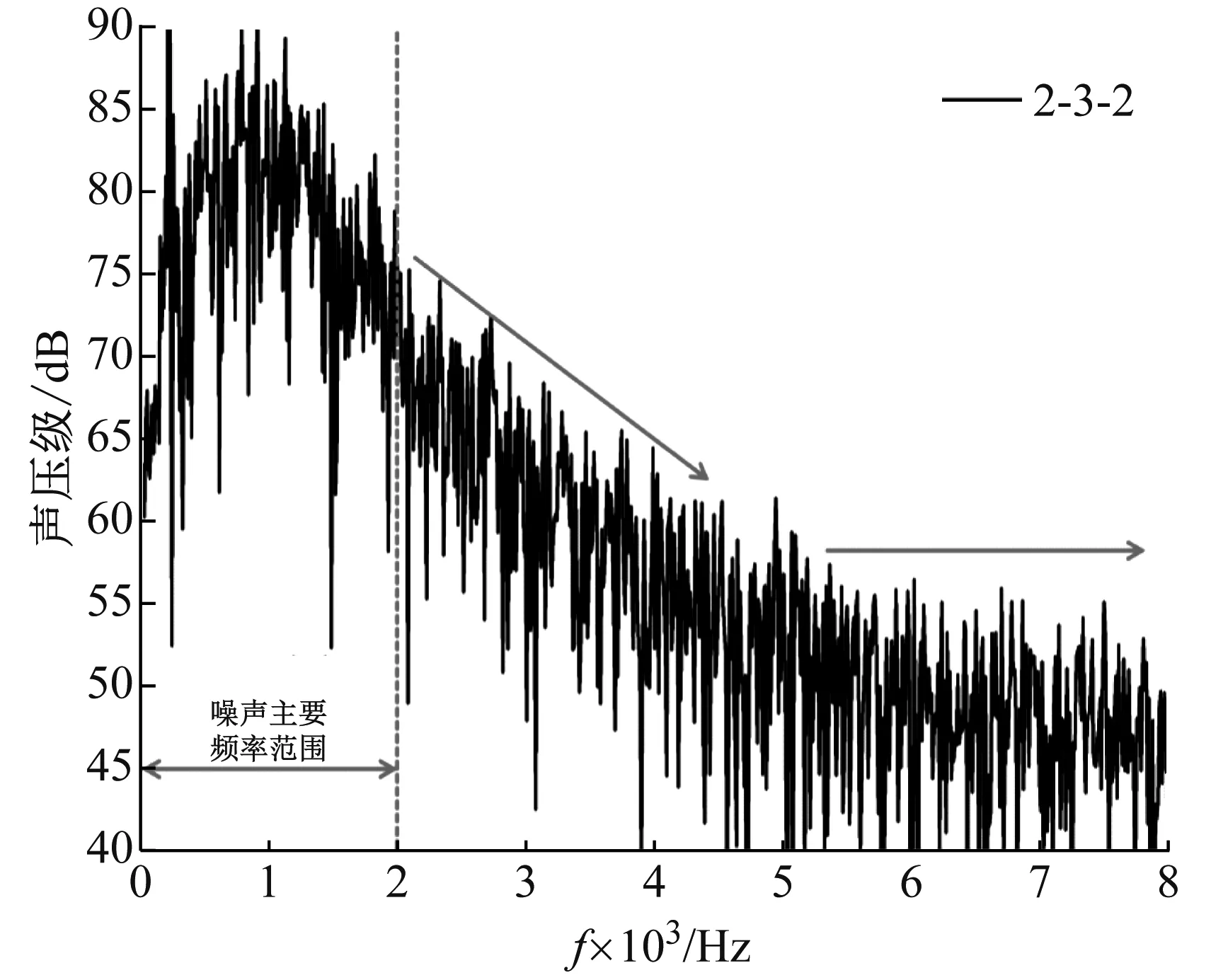
图5 数值结果验证

2.2 套筒厚度对气动噪声的影响

首先使用宽频噪声模型对控制阀内噪声源进行分析，不同套筒厚度模型的对称面声功率级云图如图6所示。由图6(a)可知，气动噪声随着流线方向(入口-阀腔-套筒小孔-出口)不断增大。声功率级(acoustic power level，APL)最大区域集中在套筒小孔流道附近流域。针对套筒底座之前的流道，阀腔底部声功率级靠近出口侧偏大。套筒内部流场靠近入口侧的声功率级大于靠近出口侧的声功率，且入口侧套筒小孔流道及其之后流域的声功率级大于出口侧套筒小孔流道及其之后流域的声功率级。大孔径套筒小孔流道处的高声功率级流域范围要大于小孔径套筒小孔流道处的高声功率级流域范围，出口流道内的声功率级仍保持在较高的水平。

(a) 2-1-2

随着套筒厚度的增加，套筒小孔流道及其出口附近高声功率级流域不断增大；阀腔内流域声功率级逐渐降低，不均匀分布现象明显好转；套筒内部流场靠近出口侧的声功率级不断降低，导致套筒内部流域声功率级分布不均匀度进一步提升；对称面上最大声功率级从189 dB略微下降至185 dB。

通过非稳态流场数值模拟，得到监测点声压信号，再借助傅里叶变换得到监测点的频谱图，分析监测点的频谱特性。不同开度下2-1-2模型测点1的噪声频谱图，如图7所示。该控制阀有三个最常使用的开度：最大工况开度82%，正常工况开度66%以及最小工况开度42%。由图7可知，不同开度下监测点的频谱特性变化趋势大致相同。随着噪声频率的增大，噪声的声压级都是先增大后减小，最后保持相对稳定。当开度不断减小时，最大声压级从120 dB减小至98 dB左右，而最大声压级发生的频率从1 400 Hz减小到1 000 Hz左右；在高频率处，声压级从60 dB下降至40 dB左右。可以发现，减小开度可以从各个频率上有效降低双层套筒式控制阀气动噪声，而且保持低声压级的高频率范围越来越大。根据相关标准规定，距离阀门外壳1 m处的声压级应不超过85 dB(A)。因此，大开度时噪声超标频率范围为300～3 500 Hz，正常开度时噪声超标频率范围为500～2 500 Hz，小开度时噪声超标频率范围为500～1 500 Hz，噪声超标频率范围随着开度的减小也不断缩小。

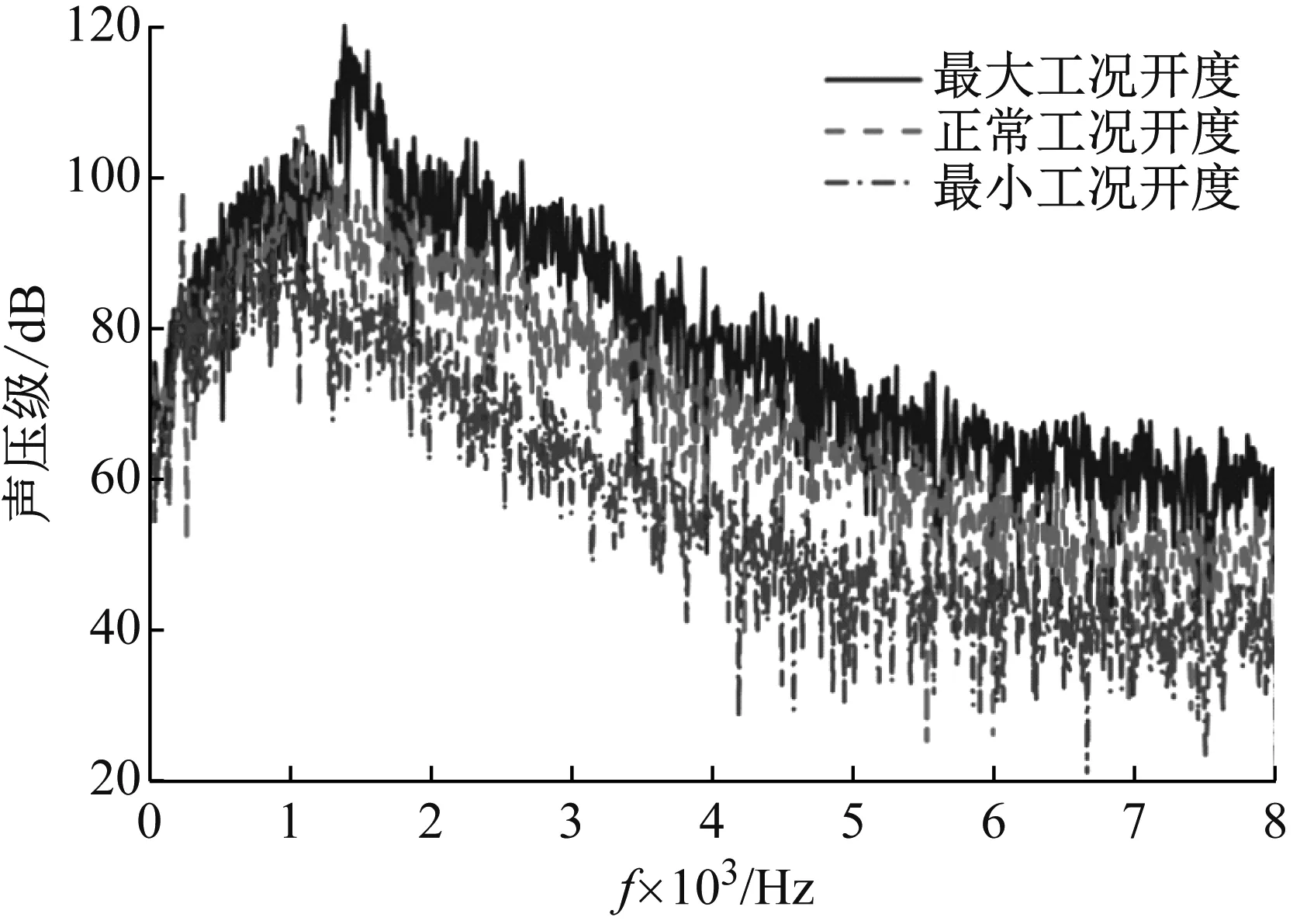
图7 不同开度下2-1-2模型测点1的噪声频谱图

基于监测点各个频率下的声压数据，通过式(4)计算得到监测点各个频率下的声压级

(4)

式中：SPL为声压级；p为声压；pref为空气中参考声压，一般取2×10-5Pa。而监测点的总声压级可通过式(5)得到

(5)

式中：OSPL为总声压级；pi为第i个采样频率点声压；n为采样频率个数。

不同开度下不同套筒厚度模型总声压级的变化，如图8所示。由图8可知，在大开度时套筒厚度的变化对双层套筒式控制阀没有抑制作用。随着开度的缩小，增大套筒厚度对于减小控制阀噪声有一定的效果，但降噪效果与增大套筒间距相比并不明显，最大降噪幅度约为2.2 dB。增大套筒厚度的降噪效果明显小于增大套筒间距的降噪效果。

图8 不同开度下不同套筒厚度模型总声压级的变化

套筒厚度的变化对于测点1的噪声频谱特性趋势基本没有影响，如图9所示。当厚度为5 mm时，所有频率上的声压级都基本控制在90 dB以下。套筒厚度的增加，使频率0～2 000 Hz的噪声有所降低，且主要噪声集中在这个范围；测点1高频率噪声所稳定的声压级略微从40 dB 提升到50 dB。随着套筒厚度的增加，下游管路外测点高频率范围内的噪声声压级基本上增加了10 dB左右。随着监测点的下游距离增大，各点的噪声频谱特性趋势不变，但各个频率上的声压级逐级下降，如图10所示。随着套筒厚度的增加，0～2 000 Hz范围内的声压级有所下降。

(a) 2-1-2

(a) 2-1-2

2.3 套筒间距对气动噪声的影响

不同套筒间距下顶部小孔中心线水平面声功率级云图，如图11所示。从图11可知，套筒内部流场声功率级分布并不均匀，内层套筒小孔入口处的流场声功率级明显大于套筒内部流场平均声功率级。随着套筒间距的增大，套筒内部流场声功率级分布不均匀度有所下降。最大声功率级发生的位置向不同方位套筒小孔流道转移，且套筒间隙流场的声功率级也不断提高；套筒外侧流场中的高声功率级流域不断消失，高声功率级流域往套筒附近流域不断汇集。整个平面的声功率级落在62～186 dB之内。不同开度下不同套筒间距模型总声压级的变化，如图12所示。当开度减小时，随着套筒间距增大，控制阀总声压级变化幅度越来越大。当大开度时，控制阀的总声压级随着套筒间距增大几乎没有变化，大约稳定在138 dB；当小开度时，控制阀的总声压级随着套筒间距增大明显下降，从117.65 dB下降到107.99 dB，下降幅度达8.2 %。当套筒间距为1 mm时，总声压级变化幅度为21.38 dB；当套筒间距为7 mm时，总声压级变化幅度提升至30.17 dB。因此，套筒间距的变化对于双层套筒式控制阀小开度工况下气动噪声影响较大。与图8相比，小开度下增大套筒厚度总声压级最大降噪值只有2.2 dB，而增大套筒间距总声压级最大降噪值提升到9.66 dB。后者的降噪值较前者提升了339%。

(a) 2-1-2

图12 不同开度下不同套筒间距模型总声压级的变化

不同套筒间距下小开度模型测点1的噪声频谱，如图13所示。与图9(a)相比，随着套筒间距的增大，可以发现在频率0～2 000 Hz范围内，声压级有很明显的下降。在套筒间距为5 mm和7 mm时，所有频率上的声压级都小于85 dB，满足标准要求。从趋势上来看，随着套筒间距的增加，声压级变化趋势愈发平缓，变化范围在逐渐缩小。针对不同套筒间距下小开度工况时双层套筒式控制阀下游管路中心点的声压级，采用1/3倍频图进行对比，如图14所示。从图14可知，随着下游管路中心监测点不断向下游移动，各个频率上的声压级都不断下降。每往后移动1 m，声压级下降5～10 dB。当套筒间距从1 mm增加到7 mm时，最大声压级明显降低，但在1 500～8 000 Hz范围内，声压级下降幅度明显降低。在高频率范围(6 000～8 000 Hz)内，大套筒间距模型的声压级要略高于小套筒间距模型的声压级。

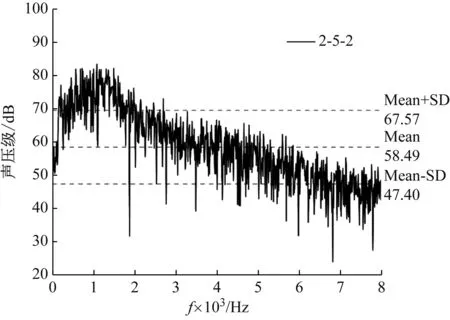
(a) 2-5-2

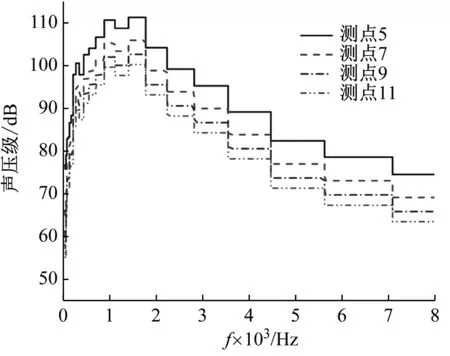
(a) 2-1-2

所有模型在不同开度下测点1的总声压级，如表4所示。从表4可知，2-7-2模型在3个工况开度下总声压级都是最小的。因此，从降噪的角度来说，采用套筒厚度2 mm和套筒间距7 mm套筒结构的二级套筒式控制阀是目前噪声相对最小的模型。此外，增大套筒厚度和套筒间距对于降噪都有效果，但增大套筒间距的效果要远好于增大套筒间距。而且，减小工况开度对于提升增大套筒厚度或套筒间距带来的降噪幅度有明显的效果。但增大套筒厚度以及套筒间距并不能减小大开度下控制阀的气动噪声，说明了大开度下，套筒厚度与套筒间距并不是影响套筒式控制阀气动噪声的关键因素。

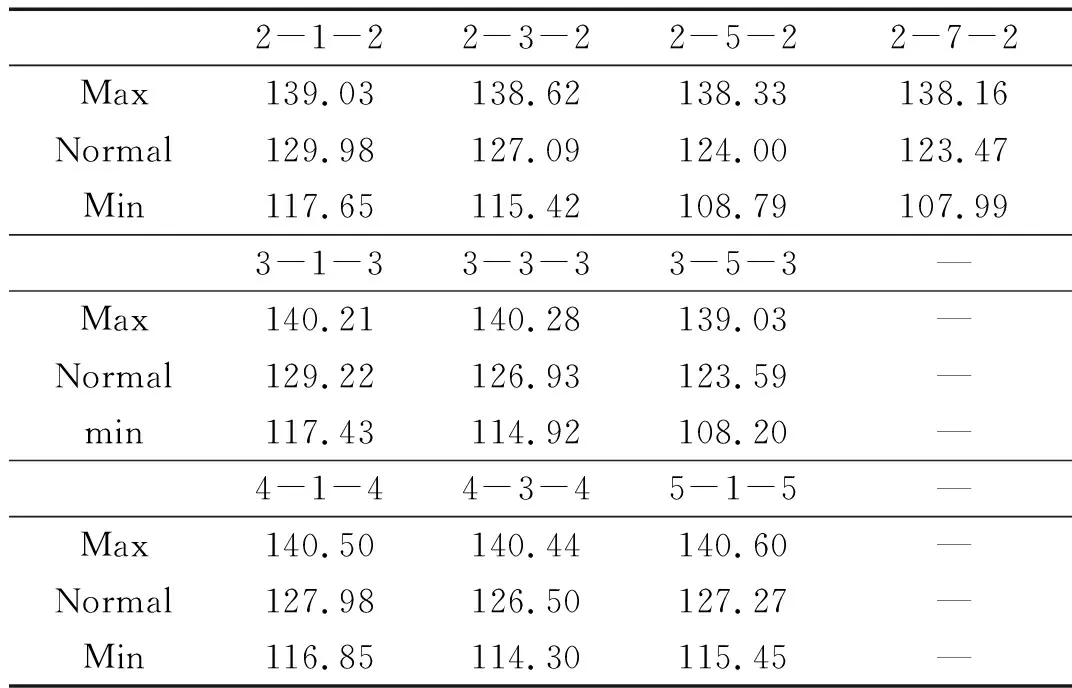
表4 各个开度下不同结构模型测点1总声压级

3 结 论

本文研究了套筒结构对双层套筒式控制阀气动噪声的影响。根据不同的套筒厚度以及套筒间距组合建立相对应的双层套筒式控制阀流道模型，使用宽频噪声模型以及声类比模型，对控制阀内部流场噪声源以及控制阀外部监测点的噪声频谱特性进行对比分析，所得到的具体研究结果如下：

内部流场噪声源主要集中在套筒小孔流道附近，声功率级达180 dB以上。增大套筒厚度，阀腔内声功率级分布不均匀度降低，套筒内部声功率级分布不均匀度增大。增大套筒间距，增大底部阀腔内声功率级分布不均匀度，降低套筒内部声功率级分布不均匀度，且套筒外高声功率级流域较小，逐渐向套筒小孔流道附近集中。从大开度减小到小开度，监测点各个频率上的声压级下降约20 dB。随着套筒厚度的增大，小开度下监测点总声压级下降最大，约2.2 dB，降幅小于2 %；监测点的频谱特性没有明显改变。增大套筒间距，大开度下监测点总声压级下降值只有0.9 dB，而小开度下监测点总声压级下降值提升至9.66 dB,降幅达8.2 %；监测点的噪声频谱特性变化趋势愈发平缓，且低频区域声压级下降。

总体而言，增大套筒厚度和套筒间距都有利于减小双层套筒式控制阀的气动噪声，且增大套筒间距的降噪效果要明显好于前者。