基于非线性超声混频技术的钢绞线张力识别研究
2022-05-04李健斌乔珍珍唐光武
钱 骥, 李健斌, 乔珍珍, 唐光武
(1. 重庆交通大学 山区桥梁及隧道工程国家重点实验室, 重庆 400074;2. 桥梁工程结构动力学国家重点实验室, 重庆 400067; 3.重庆交通大学 土木工程学院, 重庆 400074)
钢绞线广泛应用于预应力混凝土结构、桥梁拉索等重要工程结构,其应力水平直接影响着结构的耐久性和安全性。然而,在张拉及使用过程中,受各种因素影响,钢绞线难以长期保持设计应力水平,导致结构承载能力下降。因此,开展在役结构钢绞线应力水平检测对保障预应力结构安全性及耐久性至关重要。
超声导波是近年来研究较多的一种结构无损检测方法,具有传播距离远、检测速度快等优势[1]。传统的线性超声检测技术通过反映受测介质的声阻抗变化进行损伤评估,当受测材料性质变化不大时其损伤指标变化不明显[2]。非线性超声检测方法是通过超声波与损伤界面相互作用时表现的二次谐波[3]、边频调制谐波[4]及信号频移[5]等非线性特性实现损伤识别,相较于线性超声技术具有更高的敏感性。
二次谐波是较早开展研究的一种非线性超声效应。Nucera等[6-7]引入二次谐波进行钢绞线张力识别,开展了钢绞线有限元分析及张拉试验并测量二次谐波与基频产生的谐波,结果表明二次谐波非线性系数随钢绞线张拉力增大而减小。Salamone等[8]使用超声导波和嵌入式传感器在预应力梁中开展非线性超声检测,试验结果表明,基于二次谐波的非线性超声参数法是监测后张混凝土梁预应力水平的一种合适方法。
近年来,基于混频技术的声场调制方法在非线性超声研究中更受关注。混频法是指同时激励两列信号,通过分析接收信号产生的频率边带达到损伤识别目的。两列信号在受测试件中的激发和传播都保持分离,但它们在界面处会相互作用,因此该方法相较于二次谐波法,受传感器等设备的系统非线性的影响较小,对损伤识别的靶向性更高[9]。Biwa等[10]通过单列简谐波在含接触界面固体中的传播模型,推导了透(反)射信号的非线性分量的近似表达式。刘学君等[11]在该接触模型基础上考虑了两列信号入射的情况并分析了边频调制谐波声学非线性系数与界面刚度间的关系。Zhang等[12]将激振器振动与超声波结合开展了螺栓松动混频检测试验,同时利用二次谐波指标和调制边频指标评估松动螺栓的残余扭矩,两种非线性超声识别方法都能够有效的反映螺栓残余扭矩水平,而边频识别指标较二次谐波指标更稳定。焦敬品等[13]对含不同闭合裂纹长度的钢质梁进行超声混频检测,实现了对闭合裂纹的定位和长度测量。钢绞线丝间接触界面同样产生超声非线性效应,且最终反映钢绞线张力,目前,尚缺乏超声混频技术在钢绞线张力测量中的研究。
采用超声混频技术开展钢绞线张力测量方法研究。首先,基于界面刚度模型建立了钢绞线张力与边频非线性系数之间函数关系;然后,利用ABAQUS仿真模拟了钢绞线非线性超声传播过程;最后,通过逐级加载试验研究了非线性系数受张力影响规律,并分析了激励源输入功率影响。
1 理论分析
1.1 混频波传播过程推导
基于两列简谐波在钢丝界面的有限区域内的传播特性建立模型,如图1所示。两有限区域为线弹性结构(ρ为密度,E为弹性模量)。
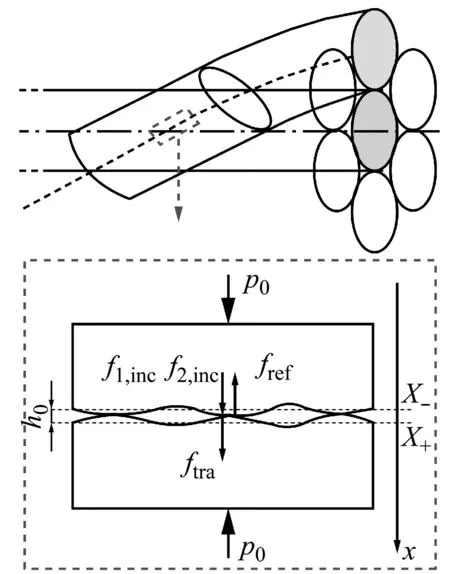
图1 钢绞线丝间接触模型
假定界面在未施加弹性波的情况下,界面两端受压力p0时,其间距为h0。在上侧沿x轴方向入射两列声波ua=f1,inc(x-ct) 、ub=f2,inc(x-ct),则
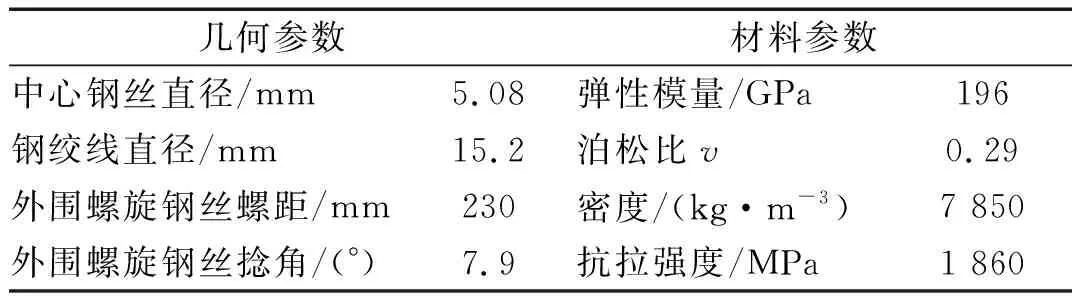
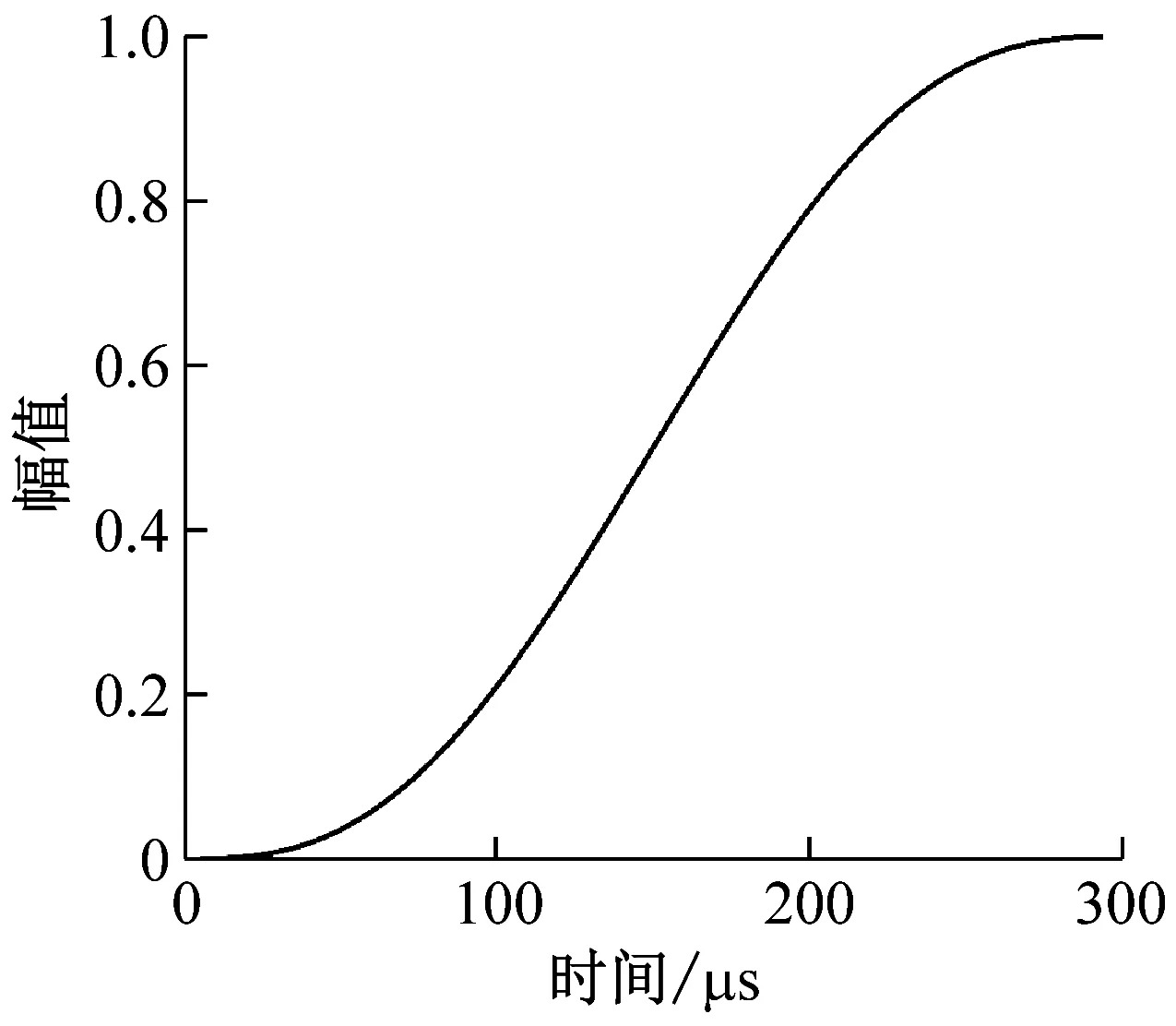
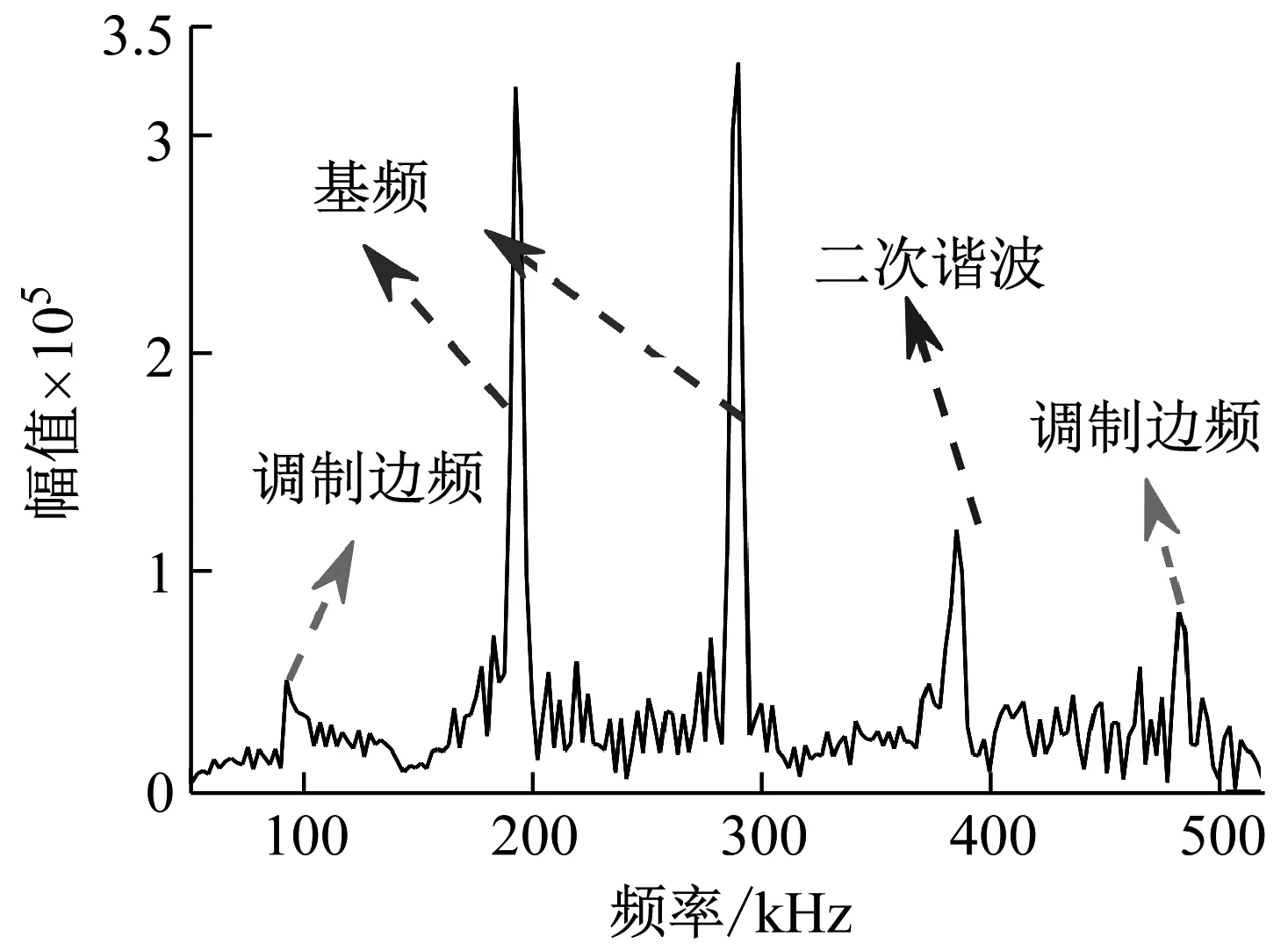
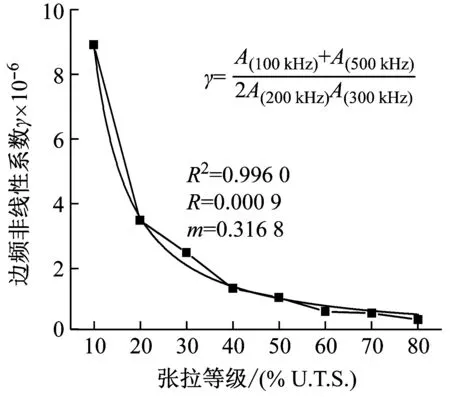
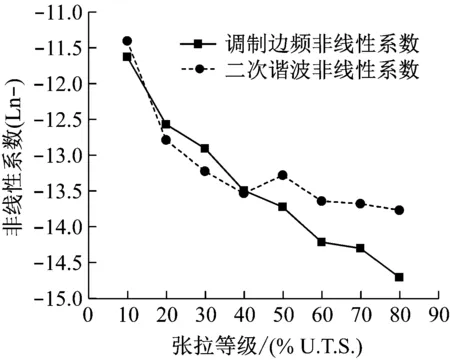
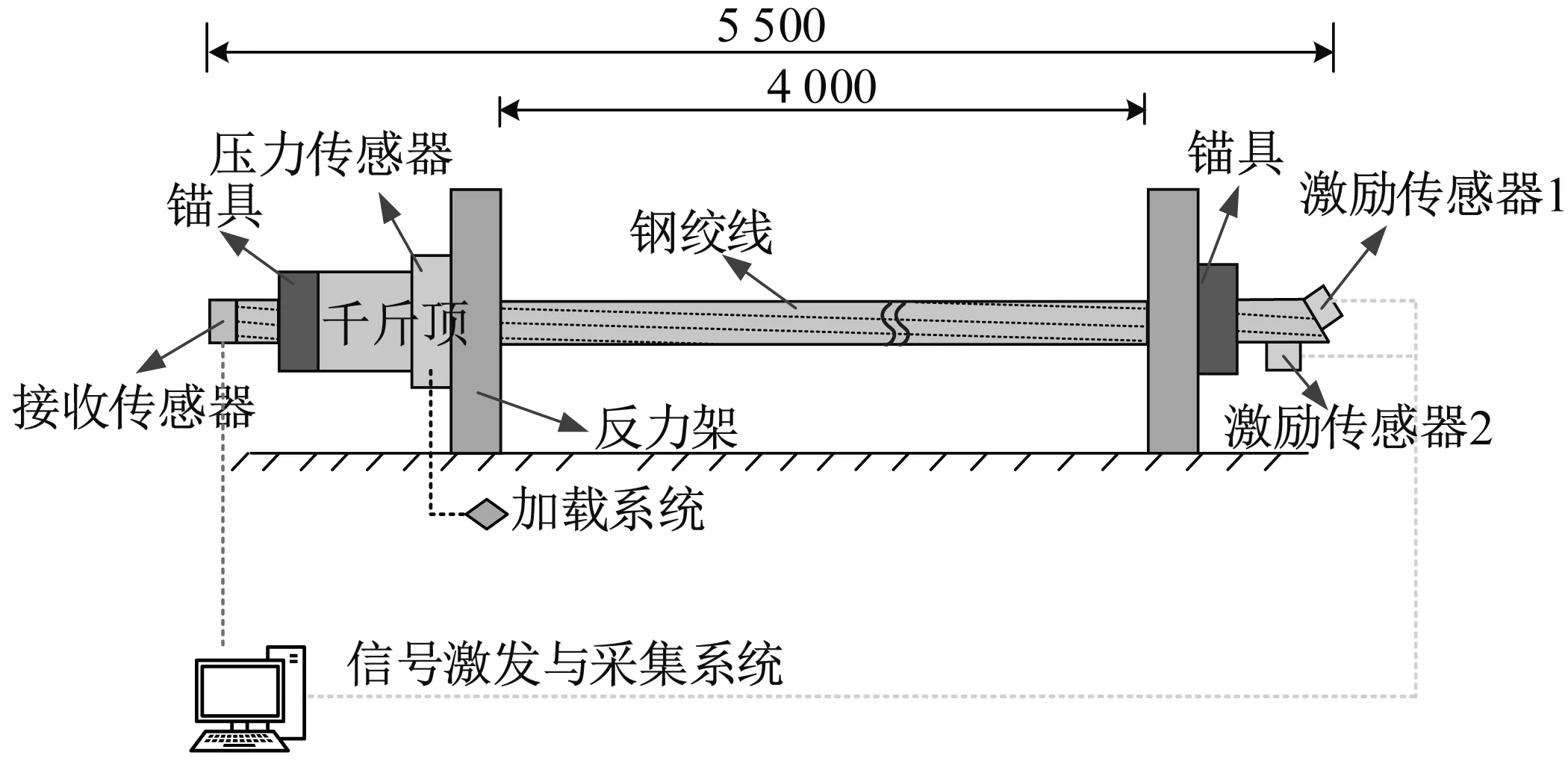
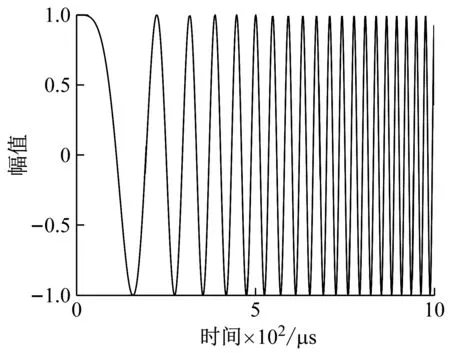
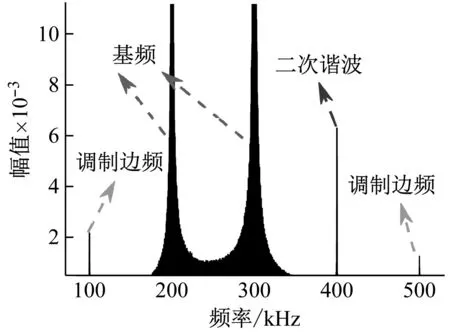
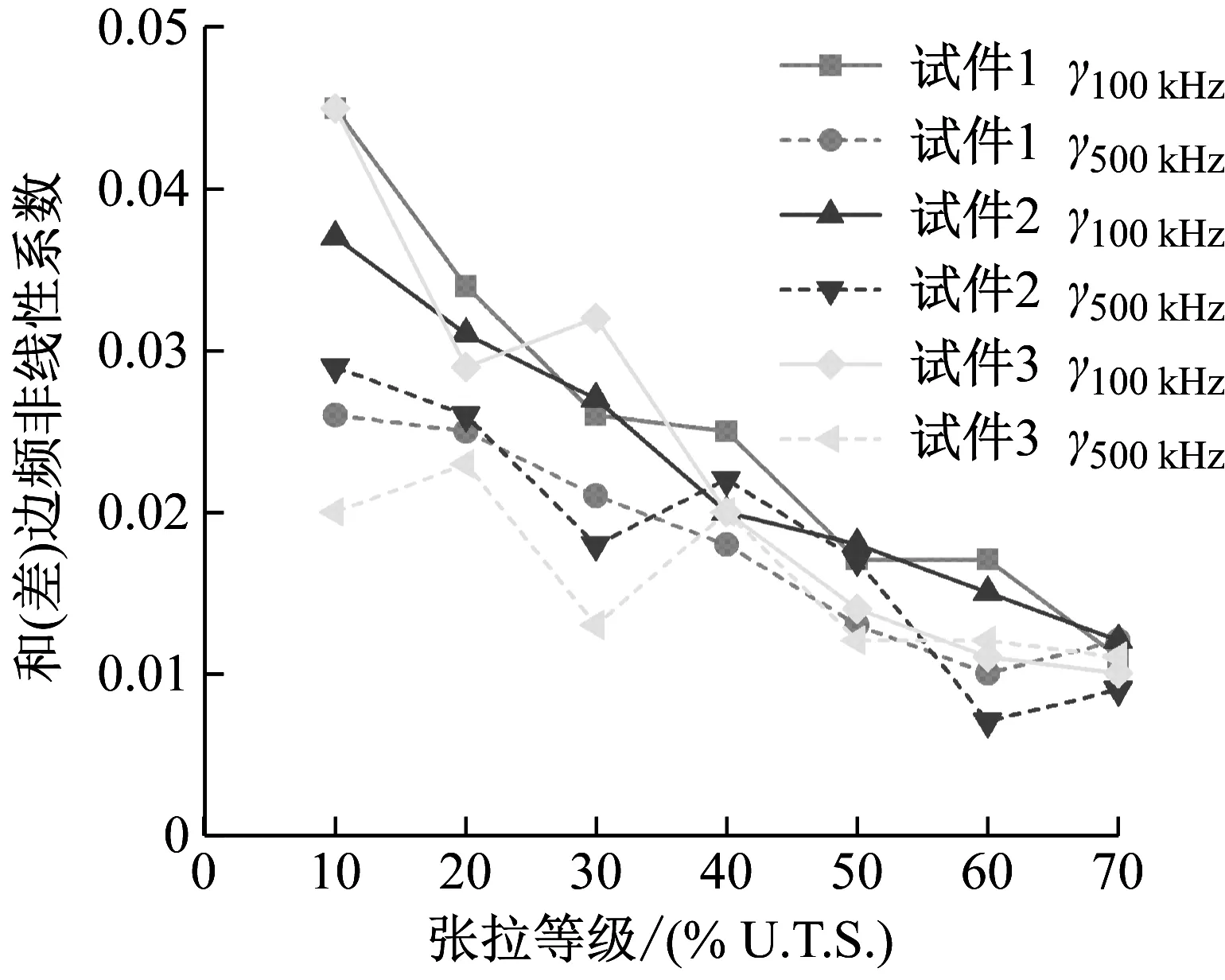
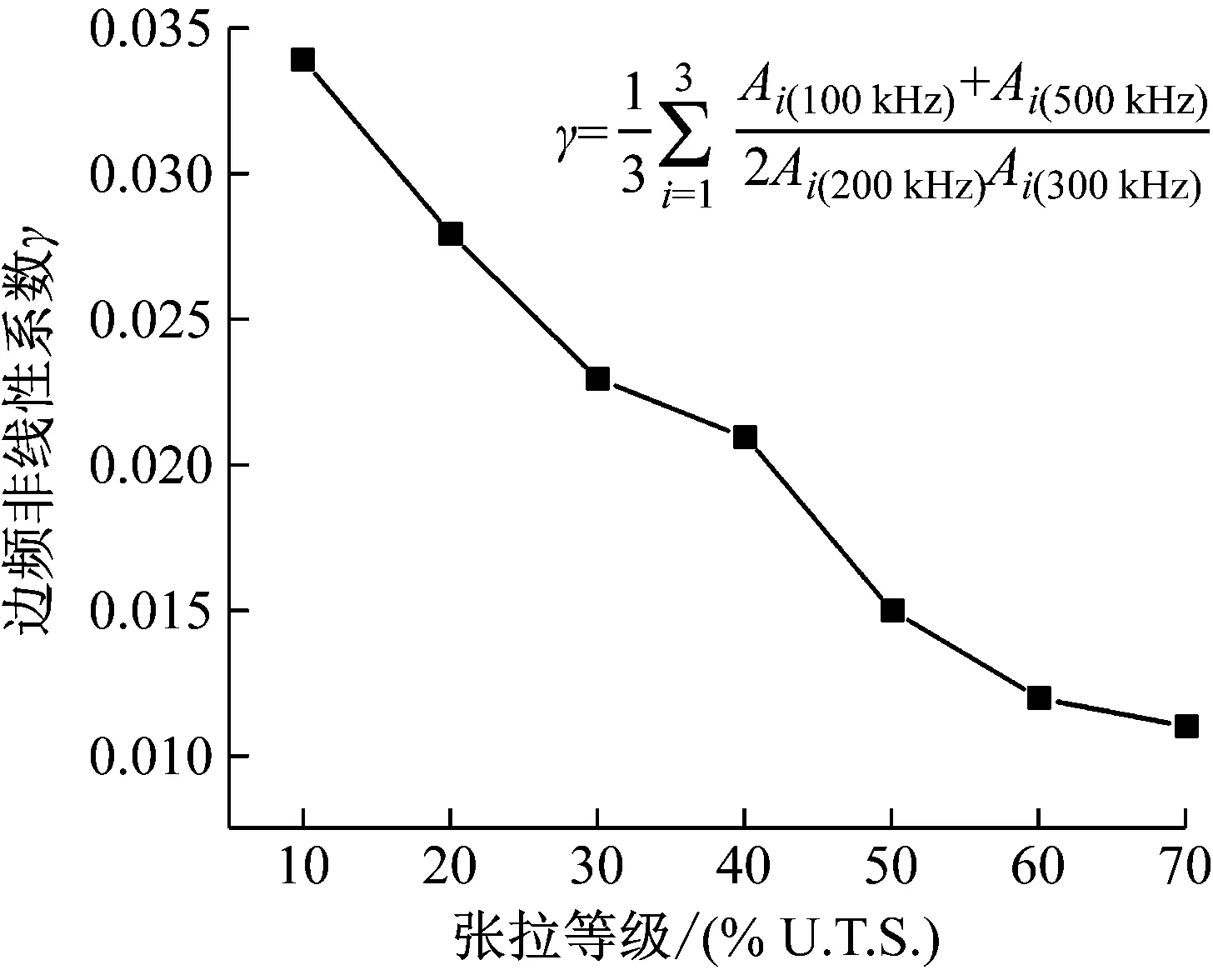
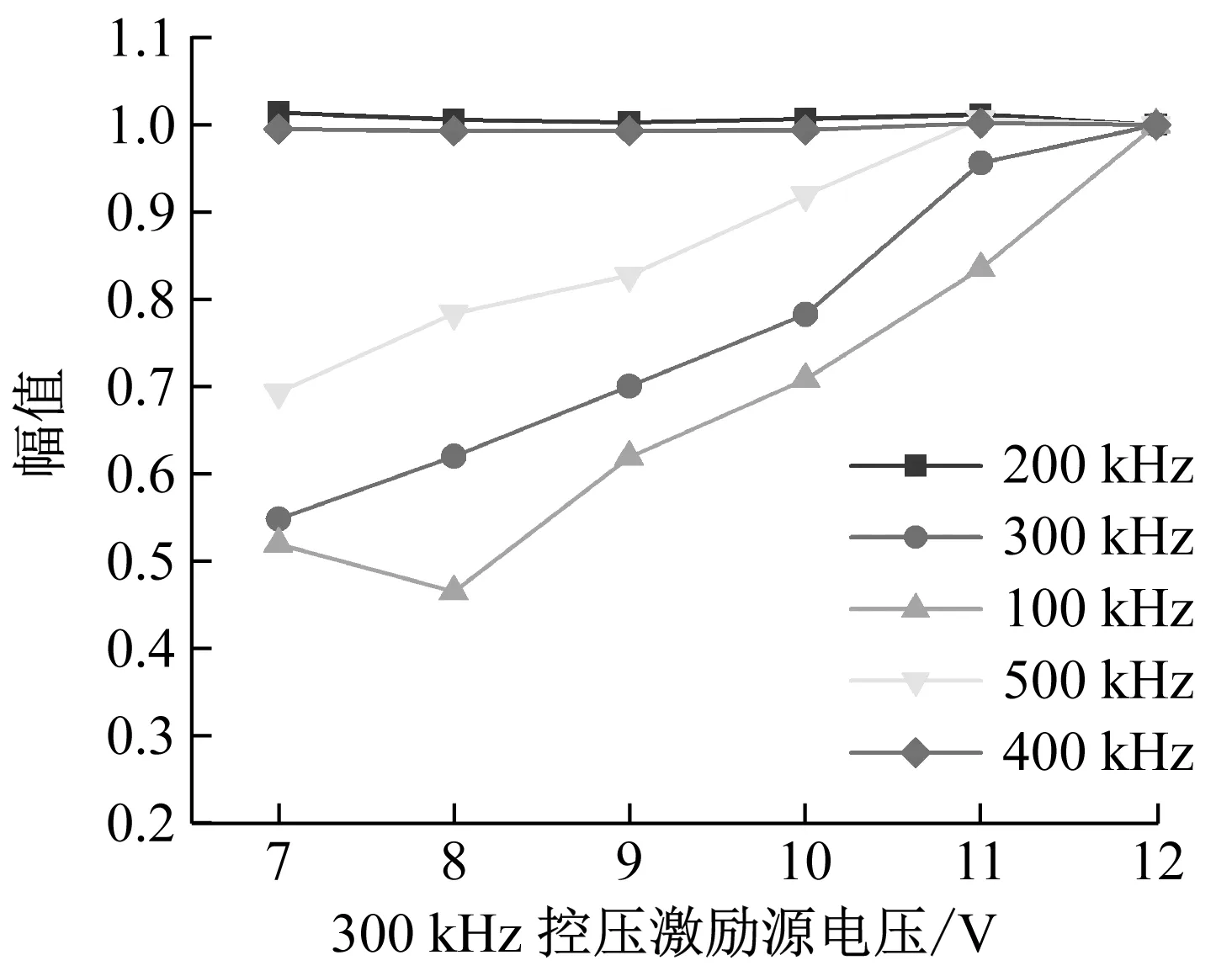
u-(x,t)=ua+ub+uc,x (1a) u+(x,t)=ud,x>X+ (1b) 式中:uc=fref(x-ct) 为反射波;ud=ftra(x-ct)为透射波;u为位移;c=(E/ρ)1/2为波速;t为时间。 考虑弹性波在界面的相互作用,得到界面的间隙与时间的关系有 h(t)=h0+u(X+,t)-u(X-,t) (2) 接触界面存在应力连续条件 σ(X+,t)=σ(X-,t)=-p(h(t)) (3) 式中:p(h0)=p0,令: X(t)={u(X+,t)+u(X-,t)}/2 (4a) Y(t)={u(X+,t)-u(X-,t)}=h(t)-h0 (4b) X,Y分别为界面的位移和界面间距随时间的变化,控制方程可以写为[14] (5a) (5b) (6a) (6b) 式中:A1,A2分别为两列入射波的幅值;ω1,ω2分别为两列入射波的角频率。因接触界面存在初始应力,故界面的非线性弹簧模型可以表述为[10] p(h)=p(h0+Y)=p0-K1Y+K2Y2 (7) 因此将式(6) 代入式(5(b))可得: (8) 上述方程为非线性非齐次微分方程,采用摄动法求解得到透射波与反射波的近似表达式 (9) (10) 从式(9)和式(10)可知,透射波ftra和反射波fref的谐波成分可由四部分组成,分别为直流成分、基频波(uω1,uω2)、二次谐波(u2ω1,u2ω2)、边频调制谐波(uω1±ω2)。其中二次谐波及边频调制谐波的出现被称为接触声非线性现象。以透射波为例,可以得到非线性谐波成分的最大幅值与入射参数的关系如下 (11a) (11b) uω1±ω2(x,t)∝A(ω1±ω2)= (11c) 式中:Aω1为基频波uω1的幅值;A2ω1为二次谐波u2ω1的幅值;A(ω1±ω2)为边频调制谐波uω1±ω2的幅值。研究对象变为另一列频率ω2以及反射波时式(11)计算结果相同。 基于边频信号幅值A(ω1±ω2)和基频信号幅值Aω1、Aω2可建立边频非线性系数γ(ω1±ω2) (12) 该非线性指标的大小仅与界面刚度有关,而与激励参数无关。而基于界面刚度模型的理论和试验研究证明,界面刚度与接触力满足幂率关系式 (13) 式中:C、m为始终为正的常数。假定钢丝接触作用为线分布力,则钢绞线的螺旋结构使丝间压应力p0与钢绞线轴向载荷Nh成比例[15] (14) 联立式(12)、式(13)和式(14),即可建立张拉力与接收信号边频非线性系数的关系式 (15) 式中:γ(ω1+ω2)和γ(ω1-ω2)为和(差)边频非线性系数,研究者常用两侧的边频非线性系数的平均值γ作为识别指标以减小检测误差。同理,可以得到张拉力与二次谐波非线性系数的关系式 (16) (17) 由式(15)和式(17)可知,非线性系数与钢绞线轴向张力呈幂函数关系。作为同阶摄动求解结果,两类非线性系数与张力的映射关系满足同样的幂律模型。不同的是,二次谐波非线性系数β还额外受基波频率的影响,这一影响因素在钢绞线内具有频散特性的导波传导过程中可能造成更多干扰。理论上,由于m始终为正,所以边频及二次谐波非线性系数随张拉力的提升而单调减小,且非线性系数不受激励信号幅值的影响。 利用ABAQUS/Explicit对钢绞线进行逐级张拉和非线性超声模拟,如图2所示。钢绞线长度L=520 mm,螺距h=260 mm,直径D=15.2 mm,不考虑材料阻尼影响,材料参数如表1所示。钢绞线轴向单元尺寸为1 mm,钢丝接触区域的网格尺寸加密到0.1 mm。钢绞线的法向接触采用“硬”接触,切向采用摩擦因数为0.6的“罚”摩擦[16]。分析过程采用全自动积分时间步长。 图2 钢绞线有限元模型 表1 钢绞线材料参数 模拟过程分为轴向张拉力施加、超声激励以及超声传播三个阶段,三个分析步时长均为300 μs。模型一端完全固定,另一端仅释放轴向位移,并约束其它方向自由度。在钢绞线的非完全固定端施加光滑幅值曲线的面荷载以模拟轴向张拉,最大拉应力为1 488 MPa,即80%极限抗拉强度(80%U.T.S),采用平滑幅值曲线完成张拉力施加,如图3(a)所示。在非完全固定端的中心钢丝圆心处,超声激励采用中心频率为200 kHz和300 kHz的调制正弦函数,为了防止信号湮灭,在已加载预应力钢绞线中激励导波时,激励信号能量级远高于预应力能量级[17],时域波形及傅里叶频谱如图3(b)和图3(c)所示。 (a) 轴向张拉力幅值曲线 有限元模拟钢绞线mises应力云图,如图4所示。从图4可知,由于轴向张拉作用,钢绞线钢丝接触面出现线状应力集中。同时,从中心钢丝端面激励出的超声波在传播过程中会向外围钢丝透射。提取出外围钢丝中距离激励点0.5 m的节点加速度时程曲线如图5所示。快速傅里叶变换(Fast Fourier Transform,FFT)频谱如图6所示。 图4 钢绞线的mises应力云图 图5 钢绞线有限元接收信号时域波形 图6 钢绞线有限元FFT频谱图 混频激励的超声波在钢绞线的有限元模型中表现出明显的非线性特征。接收信号的FFT频谱中除了基频频带(200 kHz、300 kHz)之外还出现了中心频率在基频二倍(400 kHz)附近的次谐波,以及中心频率为两列基频信号的和(500 kHz)或差(100 kHz)的调制边频。 基于式(15)和式(17)计算出各张拉等级钢绞线超声非线性系数,如图7所示。 (a) 边频非线性系数 总体来看,调制边频及二次谐波非线性系数均随着荷载等级的提升而单调下降。而随着张拉等级的上升,两类非线性系数的变化量迅速缩小,模拟结果的拟合曲线(见图7)较好地符合式(15)和式(17)建立的幂函数模型,同时与其他研究者在单次体波入射条件下利用非线性谐波测量轴压试件界面刚度的试验结果具有相同规律[18-19]。这说明钢绞线内超声导波的非线性传播过程仍符合基于一维体波入射条件建立的理论模型的基本规律。为了更直观研究两类非线性系数在高应力阶段的变化规律,将图7的纵坐标求对数,如图8所示。 图8 不同张拉等级钢绞线外围钢丝节点的对数非线性系数 比较而言,边频非线性系数在高应力阶段随张力变化更加明显,二次谐波非线性系数的变化量则相对较小。 采用大型反力架及穿心式液压千斤顶进行钢绞线加载试验。钢绞线为公称直径d=15.2 mm七芯钢绞线,长度L=5.5 m,几何及材料参数见表1。钢绞线一端锚固,一端张拉,最大张拉力为178.9 kN(70%U.T.S.)。按照每25.6 kN(10%U.T.S.)进行逐级加载。为准确加载,在液压千斤顶与反力架间设置压力传感器,试验重复进行3次。 试验采用谐振频率范围较广的WSα传感器以研究信号的多个频带特征。在张拉持载过程中利用JDS6600信号发生器同时激发两列超声信号并通过PCI-2声卡完成信号的采集和识别(试验布置如图9所示)。在钢绞线锚固处布置两个超声激励探头激励信号发生器产生的混频信号。在钢绞线张拉处设置接收探头以采集信号完成超声识别研究。 (a) 试验布置示意图 钢绞线空间螺旋捻制构造为两列入射波提供了广阔的混频空间和往复反射条件,因此增强导波相互作用即可提升非线性谐波分量。研究表明,钢绞线在100~1 000 kHz频带激励范围能量集中于L(0,1)纵波对称模态[20],故接收传感器平贴于钢绞线端面。为了增加导波辐射区域[21],将激励处钢绞线端面切削为45°斜面以布置传感器1斜入射纵向导波;与传感器1入射相对的方向的钢绞线侧面布置激发传感器2。 在试验开始前开展扫频探测以选定最佳激发频率。激励一列50~800 kHz的啁啾信号以研究传感器在钢绞线中的谐振特性,激励信号及频谱如图10所示。 (a) 宽频激励信号 由图10(b)可知,信号强度主要集中在100 Hz、200 kHz、300 kHz、400~600 kHz附近频段。也就是说,当采用200 kHz和300 kHz的混频信号作为激励源时,其接收信号的二次谐波(400 kHz)以及和差边频(100 kHz和500 kHz)的传感器幅值响应将最明显。同时,考虑调制谐波共振条件,故采用200 kHz和300 kHz的持续正弦波作为两列激励信号,采样率2 MHz,激励电压均为10 V。 混频激励下钢绞线的接收信号FFT频谱,如图11所示。从图11可知,当钢绞线受到混频激励时,将产生二次谐波、调制边频等非线性分量。为了研究张拉力变化对非线性系数的影响,根据式(12)得到了不同张拉力控制下的和(差)边频非线性系数,如图12所示。 图11 张拉钢绞线接收信号FFT频谱图 图12 张拉钢绞线和(差)边频非线性系数 试验证明随着张拉力的提升和(500 kHz)、差(100 kHz)两种边频非线性系数呈下降趋势,这与理论公式及有限元结论是统一的。理论上,两边频的信号幅值与非线性系数应该相等,然而试验信号中500 kHz的和边频信号非线性系数普遍小于同组信号100 kHz的差边频信号非线性系数,主要是因为和边频信号(500 kHz)的频率较高,在钢绞线上长距离传导后发生了更多的衰减所导致的;低应力阶段由于其边频初始幅值更高,所以两类边频非线性系数的差值较高应力阶段更加严重。根据式(15)和式(17)分别计算边频非线性系数及二次谐波非线性系数在三次试验中的平均值,如图13所示。 (a) 边频非线性系数随张拉力变化图 从图13可知,二次谐波非线性系数及边频非线性系数随张拉力增加而下降。虽然有限元与试验的开展条件不同导致了非线性系数的量值发生了变化,但试验提取的非线性系数变化规律与有限元结论仍然保持一致。在试验中,基于边频调制谐波建立的非线性系数较二次谐波表现出了更明显的规律性,证明边频非线性系数指标测量张拉力更具稳定性。 此外,有限元模拟中的两类非线性系数在低应力范围迅速下降,高应力变化量相对较小,具有高度的幂函数特征。相比之下,利用实测信号计算出的两类声学非线性系数虽然仍然保留有该类特征,但其变化量随着张力增强并没有明显减弱。这种朝线性变化的转变规律在其他研究者利用二次谐波测量钢绞线张力过程中也同样存在[22],造成该种区别的原因主要在于试验与模拟条件的不同(钢丝接触条件、激励方式等),有待进一步研究。这种变化规律对于实际环境中预应力损失的早期识别是有利的。边频非线性系数较二次谐波非线性系数更接近线性下降趋势,规律性也更强,这对工程中准确测量张力也更有利。 分别研究了两列激励信号的输入功率对提出的非线性系数精度的影响。考虑到在长距离钢绞线中接收到有效信号需要的功率门槛较高,为了在更广泛功率范围下研究非线性系数规律,本节将接收传感器布置位置缩短至距离激励传感器1 m处的钢绞线侧面。其他试验配置与“3.1”节中的描述相同,持载等级为10%U.T.S.。试验分别以200 kHz或300 kHz中任一激励波为恒压激励源,保持其输入电压始终为7 V;同时,以另一列激励波作为控压激励源并令其激励电压范围由7 V~12 V逐级增强。 (18a) (18b) (18c) 式中:Aωi,Vj为当控压激励源电压为Vj时接收信号FFT频谱中ωi的幅值,Aωi,Vmax为当控压激励源电压为最大电压(12 V)时接收信号FFT频谱中ωi的幅值;γVj和βVj是当控压激励源电压为Vj时基于式(15)和式(17)计算的二次谐波及边频调制谐波非线性系数,γVj和βVmax是当控压激励源电压为最大时的二次谐波及边频调制谐波非线性系数。 接收到的信号的FFT频谱结果如图14所示。控压激励源频率为300 kHz时,其幅值比变化见图14(a),非线性系数比变化见图14(c);控压激励源频率为200 kHz时,幅值比变化见图14(b),非线性系数比变化图14(d)。 (a) 300 kHz激励源不同电压下频谱的幅值比 首先,由图14(a)和图14(b)可知,基频信号幅值只受其相同频率的激励信号电压影响。控压激励源的电压逐级增强会导致与激励源频率相等的接收信号基频分量幅值递增,而恒压激励源所对应的基频幅值几乎不变。此外,作为边频调谐波的频带幅值会随着任一激励源电压增强而逐渐提升,而二次谐波幅值只随其对应基频的激励源电压单调变化。最后,边频非线性系数几乎不受激励功率的影响,这与理论推导结果一致(见图14(c)和图14(d));但二次谐波非线性系数在其对应基频的控制激励源处于低电压条件时偏高(见图14(d)),主要是由于试验仪器系统非线性产生了部分二次谐波分量而使得接受信号中的二次谐波频带幅值出现虚高,而后激励电压逐渐增强使得钢绞线界面非线性波动更充分,二次谐波非线性系数开始回落,这意味着二次谐波方法对仪器的电压要求更高。 基于非线性超声混频技术开展了钢绞线张力水平测量研究,结论如下: (1) 基于简谐波在固体界面间非线性传导模型,考虑钢绞线轴向张力与钢丝界面力对应关系,建立了超声非线性系数与钢绞线张力之间幂函数关系。 (2) 有限元仿真表明,超声波沿丝间接触界面向外围钢丝传播,钢绞线内产生了明显的二次谐波及边频调制谐波,边频及二次谐波非线性系数随张力增大而单调下降,符合非线性系数与张力间的幂函数理论关系式。 (3) 进行加载条件下钢绞线混频波试验,验证了理论及有限元结果中非线性系数随张力增加而下降的规律。对比分析表明,边频非线性系数较二次谐波非线性系数在张力测量过程中规律性更强,受激励源功率变化的影响更小。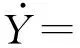
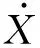
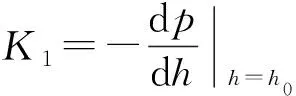
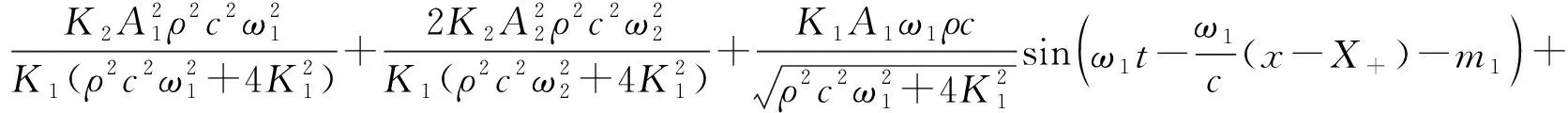
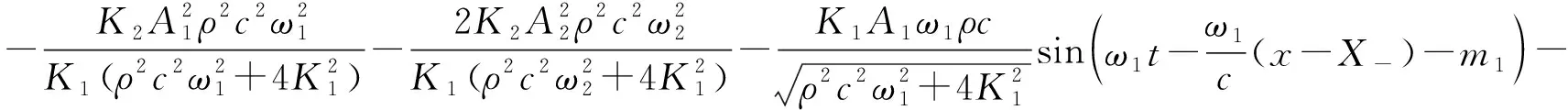
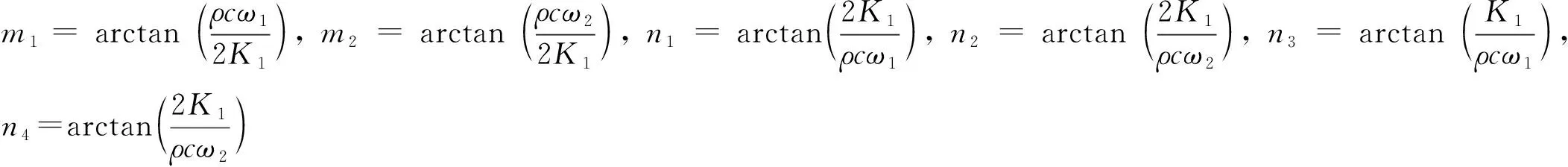
1.2 张力识别指标建立
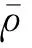
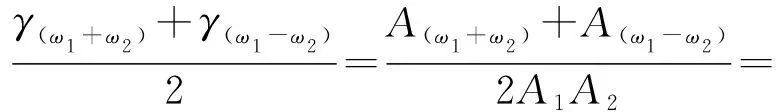
2 有限元分析
2.1 非线性超声现象模拟



2.2 张力识别
3 钢绞线张拉试验
3.1 试验方案
3.2 张力识别结果
3.3 激励源输入功率的影响
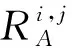
4 结 论
