分布式HDP领导-跟随者系统最优一致控制研究
2022-05-03翁腾飞陈国荣
韩 琦,曹 瑞,翁腾飞,陈国荣,王 慧
(1.重庆科技学院 智能技术与工程学院,重庆 401331;2.重庆科技学院 电气工程学院,重庆 401331;3.重庆师范大学 数学科学学院 ,重庆 401331)
0 引 言
随着人工智能技术的兴起与发展,其研究领域已经由人的智能延伸到机器智能,由人类、动物乃至工业集群行为延伸到智能群体共识协同行为。智能体及多智能体系统的相关课题受到各个领域研究学者的共同关注[1-4]。智能体指具有向环境学习的能力、能独立做出判断以及产生行为动作的智能单元,如智能语音机器人、无人机等。受智能体技术限制,单个智能体无法实现大规模、复杂化的任务。广大学者于是将目光投向智能群也就是多智能体系统的研究,研究多个智能体如何协同合作,共同达到同一目标,一致性作为协同控制的前提便成为研究热点之一。文献[5]在2004年首次提出一致性问题的理论框架和最基本的一次性协议。此后部分学者将领导者概念引入多智能体系统的一致控制中,演化出单个领导者情况下的领导-跟随者问题,以及多领导者情况下的包含控制问题[6]。
多智能体系统领导-跟随者一致就是让智能体通过与相邻智能体的通信最终实现与领导者状态的同步。文献[7]研究了分数阶多智能体系统的领导-跟随者事件触发控制问题,设计了无芝诺行为的自适应事件触发控制器,并采用分数李雅普诺夫直接法分析了系统的稳定性。
自适应动态规划(adaptive dynamic programming, ADP)是目前求解最优控制的有效方法并且在智能电网等领域得到广泛应用,ADP在求解优化控制问题上有独特优势,在行为未知的系统控制问题中有出色的表现,对于各种复杂系统具有广泛的适用性,且具有很强的自学习和自适应能力,能够自适应地学习和改进控制策略。ADP中广泛使用的迭代方法包括值迭代和策略迭代[8],以此来间接获得最优性能指标函数[9]。文献[10]首先给出了最优控制值迭代方法。启发式动态规划(heuristic dynamic programming, HDP)是ADP方法应用最广泛的结构,一般包括评价网、控制网和模型网络[11]。文献[12]采用动作相关启发式动态规划(action dependent heuristic dynamic programming, ADHDP)方法求解线性离散多智能体系统的多领导者包含控制问题,设计了值迭代和策略迭代方法,证明了值函数在迭代过程中会不断减小来保证算法的收敛性。文献[13]提出基于事件触发的HDP算法求解系统行为未知的离散时间非线性系统的优化控制问题,并运用Lyapunov稳定性理论证明:评价和执行网络权重矩阵渐进稳定且非线性系统是一致有界的。文献[14]运用线性二次调节器及非零给定点调节器理论解决了线性异构多智能体系统最优输出跟踪一致问题。文献[15]结合事件触发控制思想,研究了线性多智能体系统领导-跟随者跟踪控制问题。
受到文献[12-13]的启发,本文将ADP算法引入到非线性离散多智能体系统协同控制研究中,将求解单个系统的最优控制问题拓展到求解多智能体系统最优协同控制问题。相对于单系统的控制问题,多智能体系统的每个智能体不仅需要对自身状态做出反馈,更需要对环境变化做出响应,要考虑其他智能体的影响。本文结合ADP思想,提出了分布式HDP算法,根据每个智能体的局部误差设计局部性能指标函数,将多智能体系统领导-跟随者一致控制问题转化为求解智能体局部性能指标函数最优解的优化问题,然后设计基于BP(back-propagation)神经网络的分布式HDP求解最优控制律并对算法收敛性进行了分析,最后通过仿真验证算法是可行的。
1 预备知识
1.1 图论基础
本文采用图论来描述多智能体系统中智能体的通信关系。定义一个有向图=(V,E),其中V={v1,v2,…,vN}表示有向拓扑图中结点的集合,N表示图中的结点数,A=[aij]∈RN×N表示邻接矩阵,智能体j与i有连接,aij=1,否则,aij=0。Ni={j∈V,(j,i)∈E}表示不包含智能体i的其他所有智能体的集合。图的Laplace矩阵为L=[lij]∈RN×N,其中当i=j时,当i≠j时,lij=-aij。
1.2 符号说明
2 问题描述
考虑有N个智能体和一个领导者的离散时间非线性多智能体系统,其数学模型可以描述为
xi(k+1)=f(xi(k),ui(k))
(1)
(1)式中:xi(k),xi(k+1)∈Rn为系统状态向量;ui(k)∈Rm为系统控制输入,i=0表示多智能体系统中的领导者,i≠0表示跟随者,且u0(k)≡ρ,ρ为任意正常数;k表示离散时间多智能体系统的第k时刻。
假设1[13]系统(1)是可控可观测的。fi:Rn×Rm→Rn是一个未知的连续Lipschitz函数。在u(k)=0时,系统的状态x(k)=0是唯一的平衡点,即f(0,0)=0。
引理1[14]若图是连通的,则图的拉普拉斯矩阵L具有一个特征值0。

定义第i个智能体的局部误差为
(2)
(2)式中:ei(k)=[ei1(k),ei2(k),…,ein(k)]T∈Rn,ein(k)表示第i个智能体局部误差的第n维分量;Ki表示智能体i邻接智能体的集合。
这里可以根据 (2) 式推导出系统(1)的全局误差为
(3)
3 分布式HDP算法设计
3.1 方法提出
本章节设计分布式HDP算法求解多智能体系统(1)的一致控制问题。定义每个智能体i的局部性能指标函数
(4)
(4)式中,Ui(ei(k),ui(k))=ei(k)TQei(k)+ui(k)TPui(k)为局部效用函数,且Q∈Rn×n与P∈Rm×m都是正定矩阵。
从(2)式可知,每个智能体的局部误差和与其相连的其他智能体的状态有关。由(4)式可知,局部性能指标函数与智能体自身状态、同该智能体相连的其他智能体的状态以及控制输入都有关联,从而通过每个智能体的局部误差以及控制律构建系统局部性能指标函数(4)式,将(3)式中误差系统e(k)收敛的一致控制问题转变为求解局部性能指标函数(4)式最优解的问题。

ui(k+1)))
(5)
(6)
(6)式通常被称为离散时间的哈密顿-雅克比-贝尔曼(Hamilton-Jacobi-Bellman equation, HJB)方程。
当控制律ui(k)不受约束时,哈密尔顿函数为
Hi(ei(k),ui(k),ΔVi(ei(k+1)))=
ei(k)TQei(k)+ui(k)TPui(k)+
ΔVi(ei(k+1))·ei(k+1)
(7)
(7)式中,ΔVi(ei(k+1))=Vi(ei(k+1))-Vi(ei(k)),并且有Vi(0)=0。
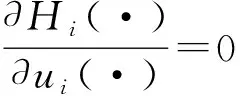
(8)
由贝尔曼最优性原理可知,对于最优局部性能指标函数(4)式的最优控制策略为
(9)
下面设计ADP算法来求解最优控制策略。
定义2[12]对于∀i,控制策略ui(k)是可允许控制策略,假设下列条件同时成立。
1)ei(k)=0时,ui(k)=0;
2)ui(k)对于误差状态空间Ei是连续的;
3)ui(k)能够使系统(1)稳定并且保证局部性能指标函数(4)式有限。
结合(4)—(5)式,最优控制策略和最优局部性指标函数的迭代寻优过程可以描述为
(10)
(11)
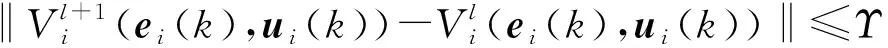
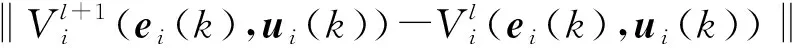
3.2 收敛性分析
本小节对(10)—(11)式的迭代方法进行收敛性分析。
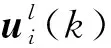
定理1对于任意给定的初始控制律ui(0),如果满足条件
(12)
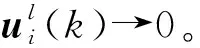
令k=t,当k→∞时有
(13)
然后令k=t-1,根据(10)—(13)式得
(14)
由(14)式的推导可知,当k=t-1时,(12)式成立。
假设k=s+1时(12) 式成立,其中∀s∈Z,Z为正整数,将k代入(12)式得
ui(s+1))
(15)
当k=s时,根据(10)—(12)、(15)式可知
(16)
证毕。
3.3 分布式HDP算法结构描述
本小节通过设计基于BP神经网络的分布式HDP算法来实现3.1提出的寻优过程,控制器中的所有网络都采用3层BP神经网络,其中模型网络的作用是辨识系统(1),评价网络用来逼近局部性能指标函数(4),执行网络用来逼近方程(6)的最优控制律。图1为分布式HDP算法结构图,其中实线表示数据正向传递,虚线表示神经网络权值反向学习调整过程。
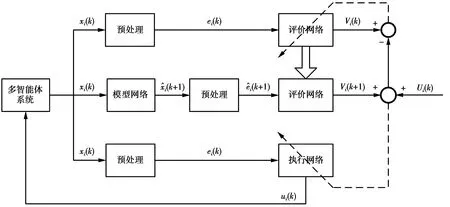
图1 分布式HDP算法结构图Fig.1 Distributed HDP controller structure diagram
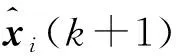
模型网络设计。智能体动力学模型(1)可运用BP神经网络来近似表示为
(17)
(18)
本文模型网络的反向传播采用梯度下降法来实现,其目标是最小化误差函数Emi(k),表示为
(19)

(20)
评价网络设计。评价网络的作用是逼近局部性能指标函数,定义评价网络的输出为
(21)
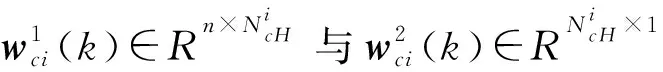
设定评价网络误差函数为
eci(k)=Vi(ei(k))-(Vi(ei(k+1))+Ui(k))
(22)
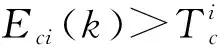
(23)
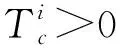
执行网络设计。执行网络将多智能体系统的实时局部误差ei(k)数据作为输入,定义执行网络输出为
(24)
(25)
(26)
3.4 算法实现
本小结介绍算法在多智能体系统中的实现步骤。
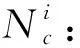
算法的实现步骤如下。
1.参数初始化;
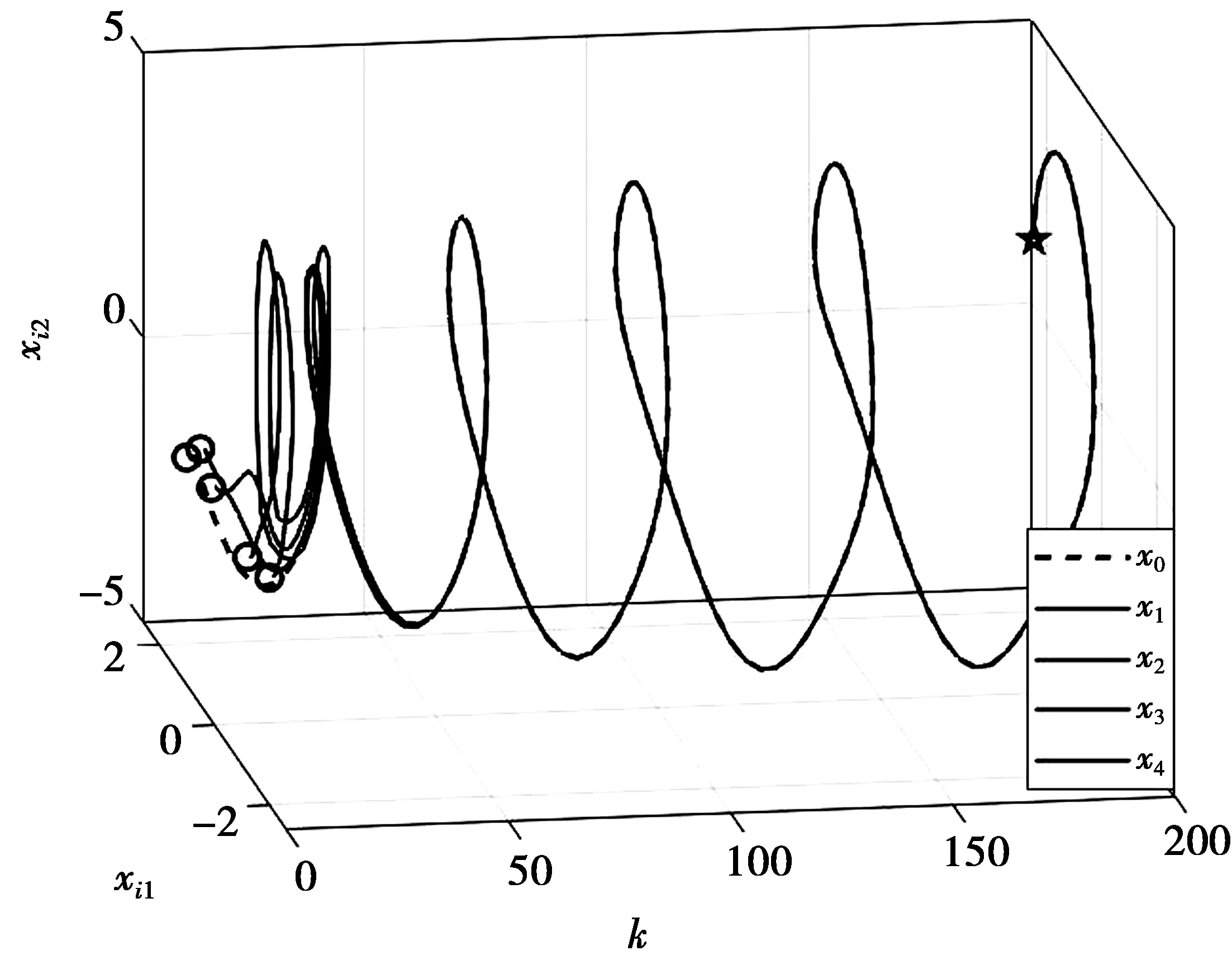
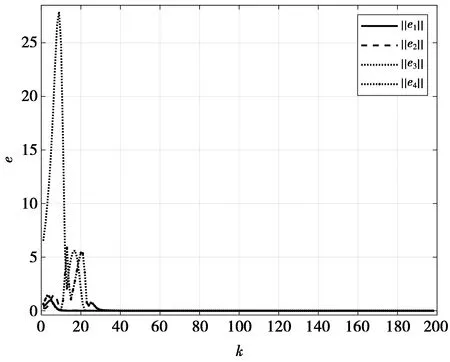
2.当k 3.根据(2)式计算ei(k)和ei(k+1); 4.根据评价网络(21)式计算Vi(ei(k))和Vi(ei(k+1)); 5.根据执行网络(24)式计算ui(ei(k)); 6.根据(22)式计算Eci(k)并且置cir=0; 9.跳转到步骤7; 10.根据(25)式计算Eai(k)并且置cir=0; 13.跳转到步骤13; 14.将ui(ei(k))输入到多智能体系统,令k=k+1,记录xi(k); 15.跳转到步骤2。 注释2虽然分布式控制器中3种神经网络(模型网络,评价网络和执行网络)的基本结构类似,都由3层BP神经网络结构组成,但是通过设定不同的误差函数(19)、(22)与(25)式,利用迭代学习使BP神经网络实现完全不同的3种功能,模型网络通过状态数据来学习辨识智能体的非线性动态特性,评价网络学习逼近局部性能指标函数(4)式,执行网络通过迭代学习寻找函数(4)式的最优值,也就是最优控制律。 注释3本文中的神经网络都只需要更新隐藏层到输出层的权重矩阵。因为只更新一层权重就足够实现预期的目标,而且可以有效减小算法的运算量。 为了验证分布式HDP控制器的可行性,本章节通过Matlab数值仿真进行算法的理论验证。 数值仿真中的符号定义如表1所示,参数设定值见表2。 表1 符号定义 表2 实验中参数的设定值 考虑具有两个跟随者,一个领导者的多智能体系统。智能体i∈{0,1,2,3,4}的数学方程为扭摆系统[13],,表示为 (27) 本实验仿真中每个智能体的控制器都采用相同的参数设定,包括神经网络的学习率、迭代次数、结点数和误差阈值。其中模型网络、评价网络以及执行网络所有神经网络初始权重为[-1,1]之间的随机数。 本部分运用分布式HDP算法实现了一阶离散非线性领导-跟随者多智能体系统的一致控制。图3为状态演化图,图4为空间演化图。 图3—图4中,领导者状态轨迹为虚线,其他智能体为实线(智能体地位相同、实线不区分),智能体1-4的状态轨迹最终与领导者实现了一致。 随着多智能体系统逐步演化,分布式HDP算法自适应产生智能体控制输入如图5所示。多智能体系统的局部误差如图6所示。 图3 领导-跟随者状态演化图Fig.3 Leader-follower state evolution diagram 图4 领导-跟随者空间演化图Fig.4 Leader-follower state space evolution trajectory 图5 智能体控制输入Fig.5 Control input of agents 由图5—图6可见,当系统局部误差随着智能体的运动增大时,系统含有的能量增大,此时控制器通过神经网络学习自适应调整权重扩大控制律来控制系统减小系统局部误差。当多智能体系统局部误差趋于0后,执行网络也自适应调整输出为0,从而实现了领导-跟随者多智能体系统的最优一致控制。 图6 多智能体系统局部误差Fig.6 Error of multi-agent system 本文结合文献[12-13],考虑非线性多智能体系统的分布式优化控制问题,将多智能体系统局部误差带入算法求解过程,设计了分布式HDP控制器来解决多智能体系统领导-跟随者一致协同控制的问题。与传统的多智能体系统牵制控制方法不同,本文从优化控制角度考虑多智能体系统一致性,探讨如何使系统中智能体能达成一致的目标(最小化多智能体系统局部性能指标函数)。基于神经网络辨识的分布式HDP控制器能根据智能体状态数据信息自适应学习,从而寻找局部性能指标函数最优解(最优控制律),并将控制律反馈输入多智能体系统实现领导-跟随者最优一致控制。
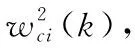
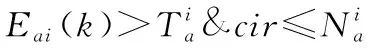

4 仿真实例
4.1 算法初始化


4.2 系统参数设置
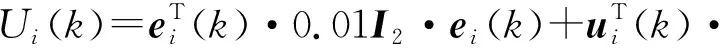
4.3 实验结果


5 结 论
