采用Pade逼近的有理非线性Fast-ICA

何选森，徐 丽

(1.广州商学院 信息技术与工程学院,广州 511363; 2.湖南大学 信息科学与工程学院,长沙 410082)

0 引 言

盲信源分离(blind sources separation,BSS)[1]是从传感器获得的观测信号中分离出未知的信源,其传感器测量的混合过程也是未知的。独立分量分析(independent component analysis,ICA)[2]是解决BSS问题的一种统计与计算技术,它揭示了构成观测信号的隐藏因素,并为观察到的多元数据定义了一个生成模型。ICA基本假设条件是信源中至多有一个服从高斯分布,其他均是非高斯,并且各信源之间相互独立。在ICA模型中,信源称为独立分量。 BSS是ICA的历史背景,而ICA是解决BSS问题的主要方法。

利用主纤维束(principle fibre bundle)[3]的概念,快速ICA (Fast-ICA)[4]算法被证明是局部二次收敛到正确地被分离出的信源上。通过对Fast-ICA在局部意义上BSS能力的推导[5-6],线性ICA的Cramer-Rao界的解析表达式也被给出[6]。基于统计效率[7]的概念,改进的Fast-ICA(efficient variant of Fast-ICA,EFICA)[7]被证明是渐近有效的,即由残差方差给出的算法精度可达到对应的Cramer-Rao下界。

Fast-ICA的理论基础是非高斯性(non-Gaussianity)最大化,而负熵(negentropy)与峰(峭)度(kurtosis)都是非高斯性的测度。由于峰度不是一个鲁棒性的测度[3],因此，非高斯性常采用负熵作为它的测度。然而,考虑到负熵本身的计算比较复杂,于是就需要对它做近似计算。在实际中,根据信源服从的分布要选择一个非二次对比函数(contract function)进行近似。当使用负熵的在线随机梯度算法时,还需要使用对比函数G(·)的导数g(·),称g(·)为影响函数,在神经网络中,则称g(·)为非线性(nonlinearity)。

Fast-ICA算法中引入了3种经典的G(·)和g(·)以处理不同分布的(非高斯)信源。由于在经典非线性中,存在有计算较复杂的非有理函数。为此,本文提出在Fast-ICA算法中采用有理函数替代经典的非线性,以节约算法的计算(运行)时间开销。为了降低有理函数的计算负担,采用最低(即1/2)阶的Pade逼近以搜索有理多项式的极限性能,从而构造出高效的有理非线性。

1 Fast-ICA算法

在无噪声情况下，ICA的线性瞬时混合模型为

x=As

(1)

(1)式中：x∈RM和s∈RM分别为观测信号和信源向量；A是RM×M的常数混合矩阵,由于它是方阵,则A存在逆阵。ICA的目的就是根据观测信号向量x估计出混合矩阵A，然后分离出信源

(2)

当峰度值为正时,对应的信号称为超高斯的信号(super-Gaussian);当峰度值为负时,称其为亚高斯的信号(sub-Gaussian)；当峰度值为零时，称其为高斯信号。在所有方差相等的随机变量中，高斯变量具有最大的熵。对于概率密度为p(y)的随机向量y，定义它的微分熵为[8]

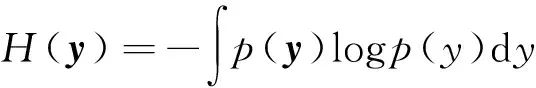
(3)

在微分熵的基础上，负熵定义为[9]

J(y)=H(yG)-H(y)

(4)

(4)式中，yG是与y具有相同协方差矩阵的高斯随机向量。一般地，负熵总是非负的，当且仅当y为高斯向量时，其负熵为零。由(3)式和(4)式可知，要精确计算负熵的值是很困难的，在实际应用中通常采用一些近似方法来计算。基于最大熵的原理，负熵的近似式为[3-4]

J(yk)≈C{E[G(yk)]-E[G(v)]}2

(5)

(5)式中：C是不相关的正常数；yk是向量y中的第k个元素；v是零均值单位方差的高斯随机变量；G(·)是任何一个非二次函数，并称其为对比函数；E(·)是数学期望(均值)的运算符。

从本质上讲，(5)式给出的就是Fast-ICA算法的目标函数。为了找到一个独立分量或一个投影追踪(projection pursuit)方向yk=wTx，对如下的函数优化(最大化)[4]

JG(w)={E[G(wTx)]-E[G(v)]}2

(6)

(6)式中，w是约束条件为E[(wTx)2]=1的M维权重向量。每个向量wi(i=1，2，…，M)给出了正交矩阵W的一行。

不同信源采用不同的对比函数才能获得较好的负熵近似。在Fast-ICA中，采用3个经典的对比函数G(·)及其非线性g(·)[3-4]，表示为

G1(u)=logcosh(u)，g1(u)=tanh(u)

G2(u)=-exp(-u2/2)，g2(u)=uexp(-u2/2)

G3(u)=u4/4，g3(u)=u3

(7)

(7)式中，G1(·)是通用的对比函数，对于超高斯和亚高斯信源都是适合的;当独立分量是超高斯或要求估计量具有较高鲁棒性时，G2(·)是很好的对比函数;若必须减少计算开销，则可使用G1(·)和G2(·)的分段线性逼近;若观测信号中没有异常值，从统计的角度来看，G3(·)仅用于估计亚高斯的独立分量。另外，从非线性的形式来看，g1(·)是一个双曲正切函数，记为tanh;而g2(·)是为分离超高斯信源而量身定制的，它接近于高斯变量的概率密度，故将其记为gauss;而g3(·)与峰度表示式相似，是一个有理函数，用于估算亚高斯信源。由于本文主要研究超高斯信源的BSS，故只涉及g1(·)和g2(·)。

Fast-ICA有紧缩(deflation)和对称(symmetric)2种算法。紧缩算法在正交条件下对独立分量逐个估计;对称算法是并行地估计独立分量。本文使用对称算法以同时估计所有的信源。文献[4]详细描述了对称Fast-ICA算法，这里仅给出最终的结果

w+=E[xg(wTx)]-E[g′(wTx)]w

w*=w+/||w+||

(8)

(8)式中：w+表示迭代的中间结果；g′(wTx)是关于w的(偏)导数；w*则是w最新的迭代值。显然，这是牛顿二阶迭代法。

考虑到信号的众多样本点，将ICA模型表示为矩阵的形式

X=AS

(9)

(9)式中：S∈RM×N和X∈RM×N分别是信源和观测信号矩阵；M为信号的个数；N为信号的样本数量，A∈RM×M仍是混合矩阵。观测数据X需要通过白化和去均值的操作转换成不相关的数据，表示为

(10)

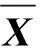
Fast-ICA算法的目标是求正交矩阵W。显然，由ICA估计的解混合矩阵B与正交矩阵W之间的关系为B=WC-1/2，于是独立信源的估计为S=WZ。由于本文采用的是白化数据Z而不是观察数据X本身，故迭代式(8)可修改为矩阵形式[10]

W+=E[g(WTZ)·ZT]-

W*=(W+W+T)-1/2W+

(11)

(11)式中：1N和1M分别表示其元素都为1的N×1和M×1矢量；符号“·”表示点积的运算。(11)式的迭代从随机酉矩阵W开始直到其收敛。

2 有理非线性的推导

Fast-ICA采用经典的非线性tanh和gauss函数以分离超高斯信源。由于tanh和gauss本身的计算复杂性，造成Fast-ICA算法的收敛速度下降。考虑到有理函数具有计算简单的特点，因此，对tanh和gauss进行有理函数逼近能够提高Fast-ICA算法的计算速度[11]。

本文中，构造有理非线性的2个原则：①采用有理函数的Fast-ICA将极大地提高算法的收敛速度;②与经典算法相比，有理非线性的Fast-ICA将保持超高斯源的BSS性能不下降。

有理逼近与连分数(continued fractions)[12]、有理插值(rational interpolation)[13]以及Pade逼近(Pade approximation)[14]等密切相关。在有理逼近中，渐近式展开(asymptotic expansion)[15]或泰勒级数展开(Taylor series expansion)[15]通常可以通过将一个给定的函数重新安排为2个类似展开式的比值(即有理函数)来极大地加速函数的计算，甚至可以将发散的函数转变为收敛函数。

所谓Pade逼近就是在给定展开式阶数情况下的有理函数，而且该有理函数的幂级数展开与指定的幂级数在一定的阶数上是相同的。给定函数f(x)的幂(麦克劳林)级数

(12)

以及一个有理多项式函数

(13)

如果函数f(x)和RM/N(x)满足以下关系

f(x)-RM/N(x)=O(xN+M+1)

(14)

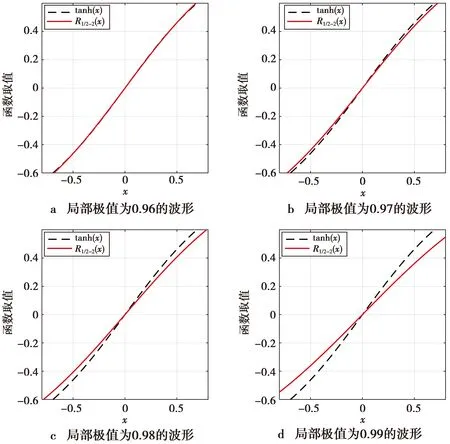
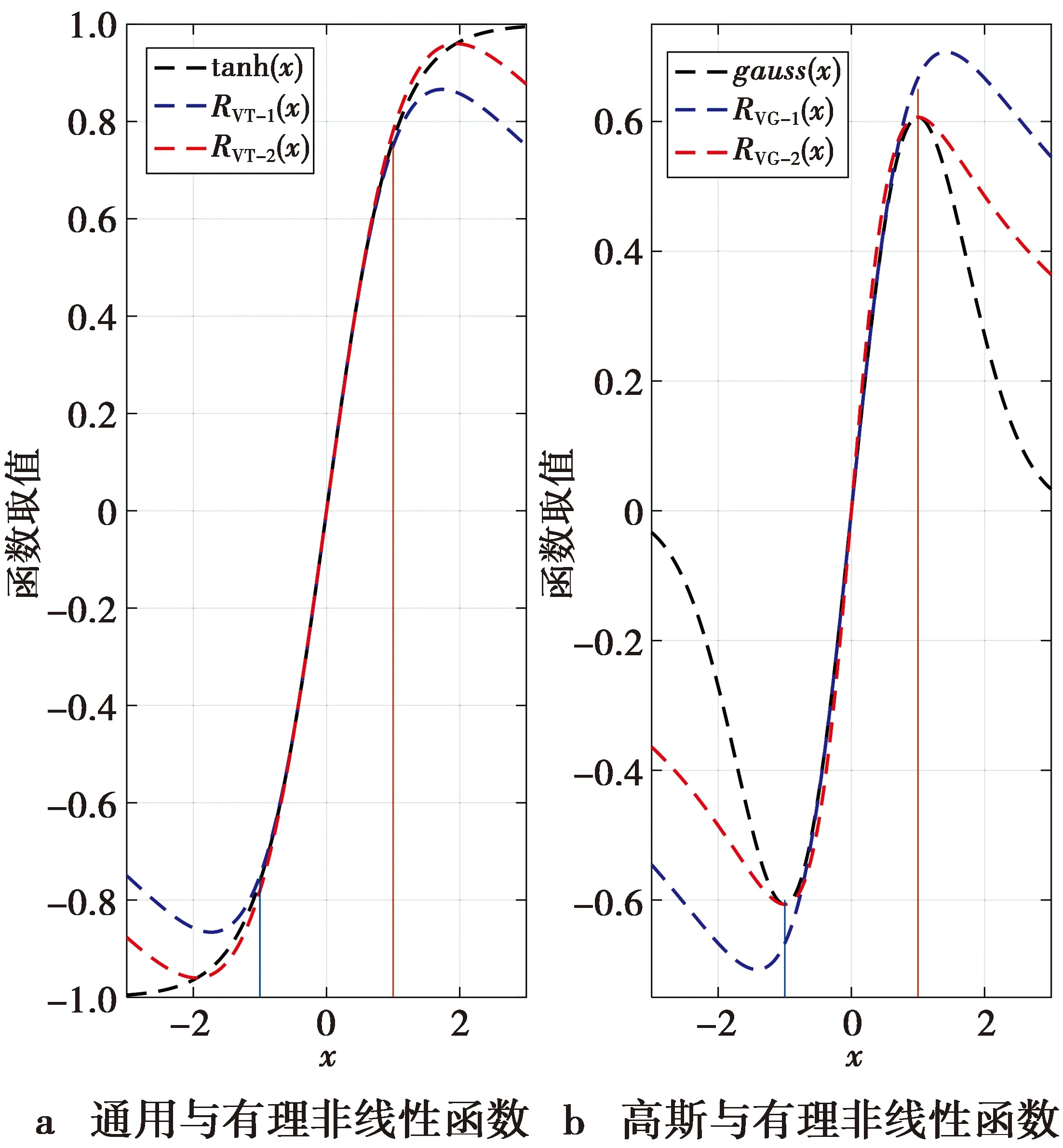
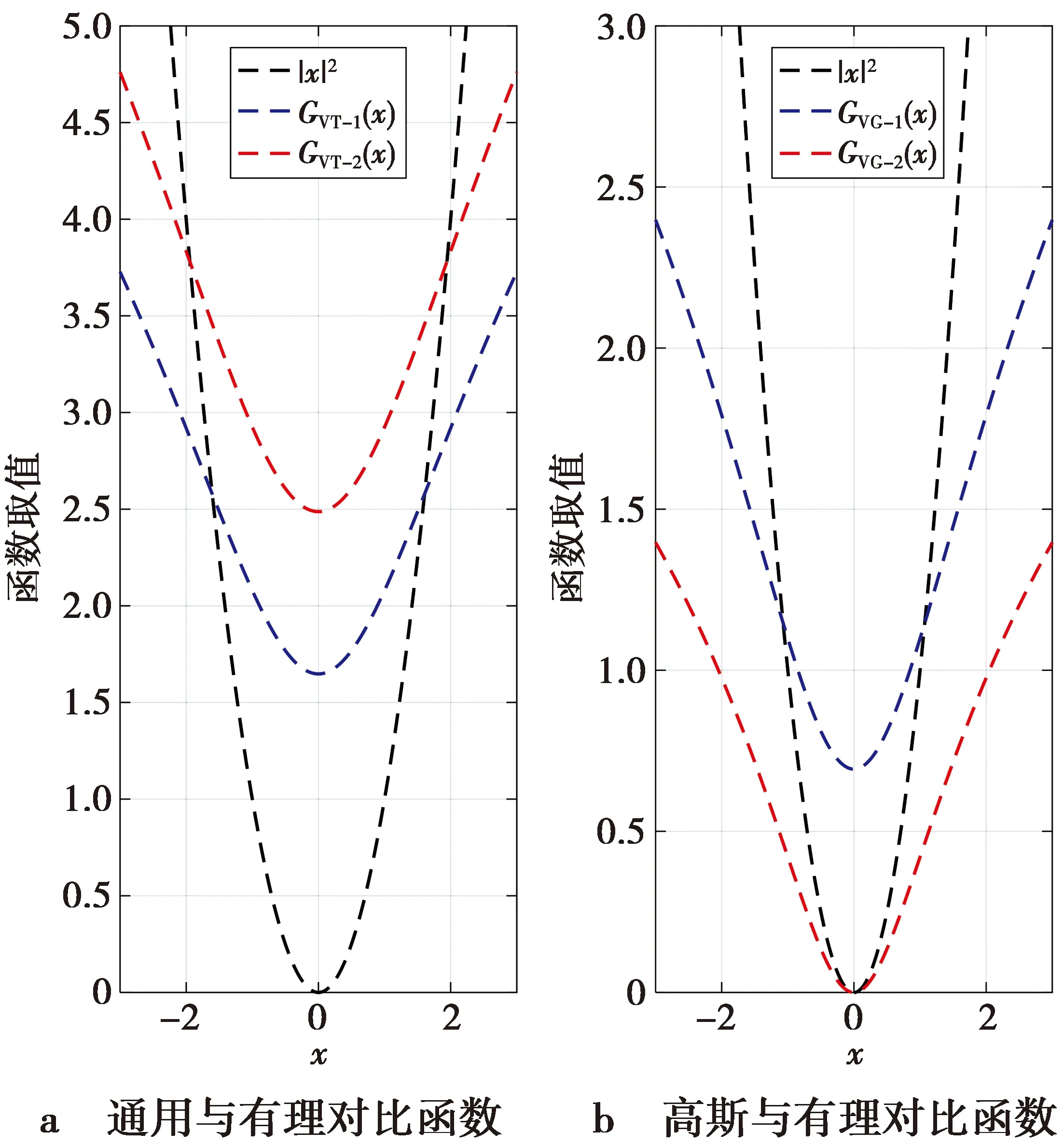
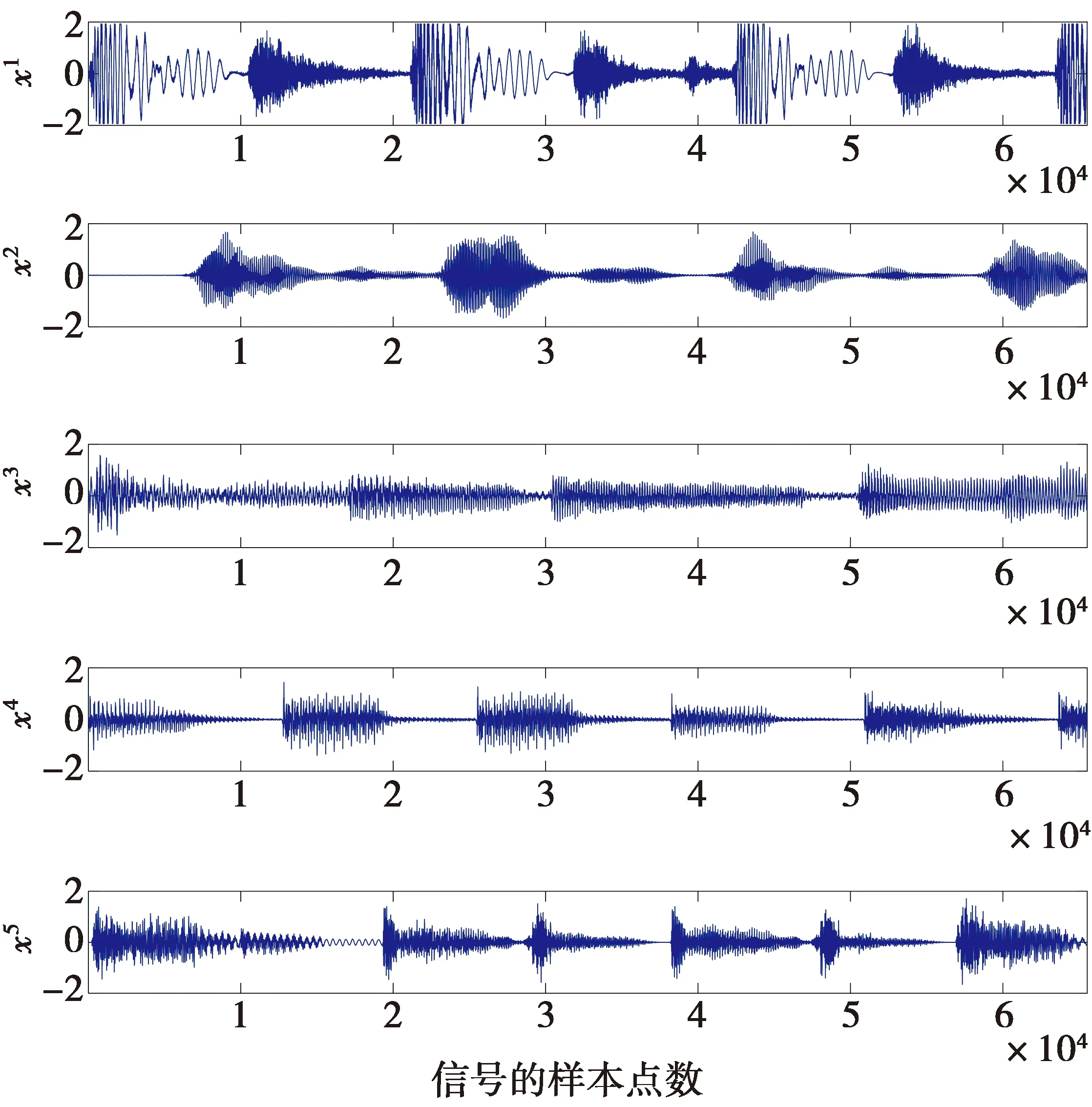
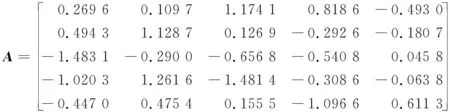
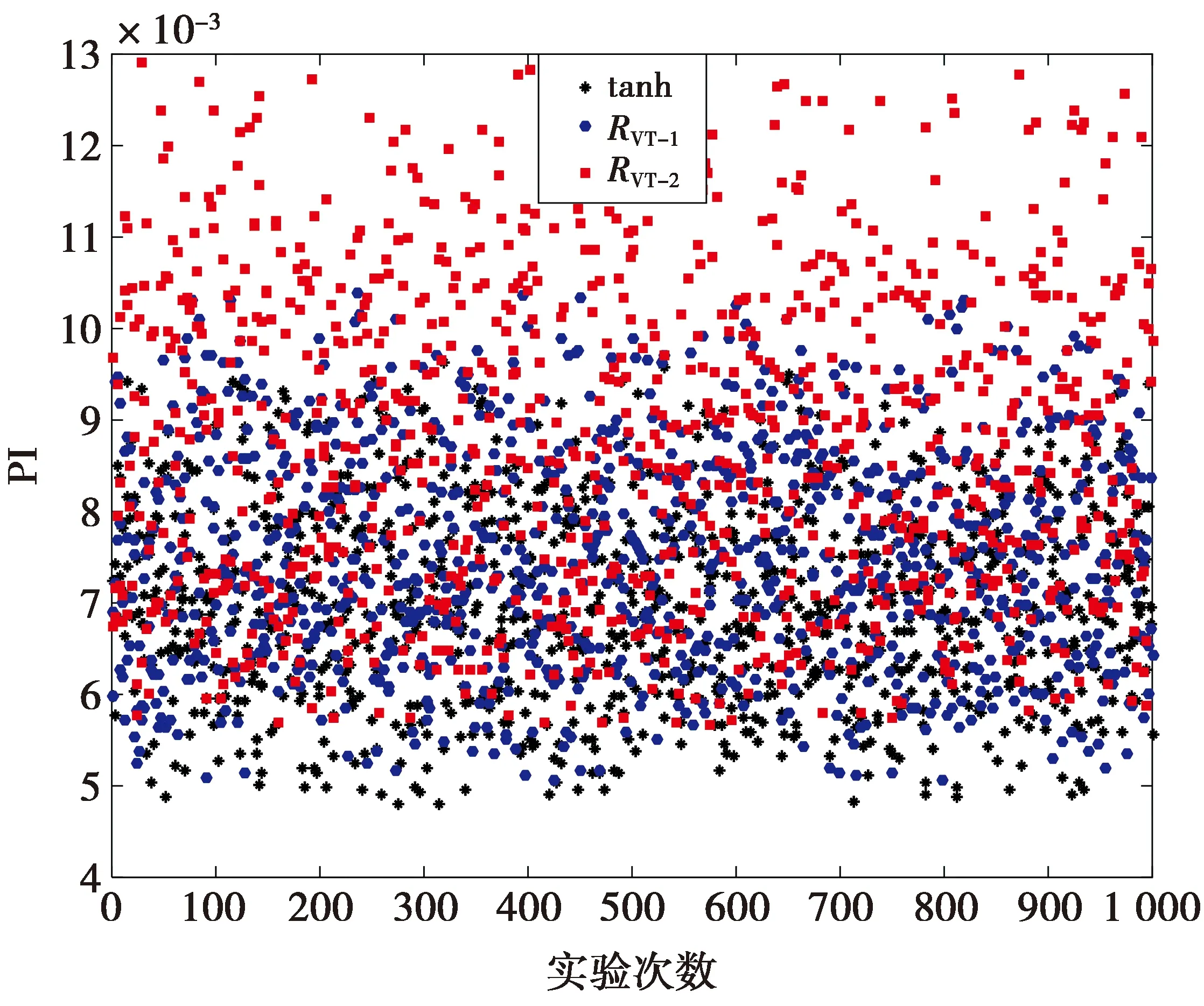
则称RM/N(x)为f(x)的Pade逼近[14]。其中M和N为整数，O(·)是高阶无穷小。在(13)式中，通常将分母多项式的系数进行归一化，即首项系数b0=1。RM/N(x)表示有理函数的分子阶数为M且分母阶数为N的Pade逼近。一般来说，总有M

从(14)式可知，Pade逼近是用有限项幂级数替代无穷项幂级数，即Pade逼近是从较少项数的幂级数展开式中提取尽可能多的信息。显然，Pade逼近可加快级数的收敛速度，即使在幂级数的收敛半径之外(若出现渐近发散的展开式，则收敛半径可能为零)也可以实现较高的逼近精度。(14)式也可以等价为以下的公式。

RM/N(0)=f(0)

(15)

(16)

由于b0=1是已知的，则(15)式和(16)式就为M+N+1个未知的系数a0，…，aM和b1，…，bN提供了M+N+1个方程。如果仅考虑对角有理逼近的情况，即M=N，则可知a0=c0，而其他系数满足[13]

(17)

(18)

(17)式和(18)式给出了幂级数系数ck(k=0，1，…，M+N)与逼近的有理多项式系数ai(i=0，1，…，M)，bj(j=1，2，…，N)之间的关系。由于系数ck是已知的，则(17)式就是求未知系数bj的一系列线性方程组。当系数bj一旦被确定下来，则从(18)式就可以求出未知系数ai的值，从而完成对有理函数分子和分母多项式系数的求解。

根据构造有理非线性的第一个原则，即有理函数分子分母多项式的项数都应尽可能地少，从而使之易于计算，因此，取Pade逼近的阶数M/N为最低的阶数1/2，即有理函数的分子为一次多项式，而分母为二次多项式。M/N=1/2的Pade逼近表示式为

(19)

在(19)式中考虑了b0=1的条件。根据(19)式，对Fast-ICA算法中经典的非线性tanh和gauss的有理化过程进行如下的推导。

函数f(x)=tanh(x)的泰勒(麦克劳林)级数展开式为

c0+c1x+c2x2+c3x3+c4x4+c5x5+O(x6)

(20)

显然，c0=c2=c4=0，c1=1，c3=-1/3，c5=2/15。由(17)式和(18)式可列出求解R1/2(x)中系数a0，a1，b1，b2的线性方程组

a0=c0

a1=c0b1+c1

(21a)

c1b1+c0b2=-c2

c2b1+c1b2=-c3

(21b)

由(21b)式求出b1=0，b2=1/3，并将其结果代入到(21a)式即可求出a0=0，a1=1。于是得到代替tanh的有理函数R1/2(x)为

(22)

类似地，函数f(x)=gauss(x)的泰勒级数展开式为

c0+c1x+c2x2+c3x3+c4x4+c5x5+O(x6)

(23)

(23)式中：c0=c2=c4=0；c1=1；c3=-1/2；c5=1/8。求解系数的方程组为

a0=c0

a1=c0b1+c1

(24a)

c1b1+c0b2=-c2

c2b1+c1b2=-c3

(24b)

由此，求解出a0=0,a1=1,b1=0,b2=1/2。

因此，得到代替gauss的有理非线性R1/2(x)为

(25)

把(22)式和(25)式归纳为R1/2(x)的一般式

(26)

显然，(26)式中有理函数分子和分母的系数都取相同的整数值α，即α的不同取值构造出不同的有理非线性。然而，另一种可能性是(26)式中分子和分母中的常数是不相同的，而且它们的取值也可以是非整数。因此，将(26)式中的R1/2-1(x)进一步扩展为

(27)

(27)式中，α，β是可调整的系数，且α≠0，β>0。如果α=β，则(27)式与(26)式是一致的，也就是说，R1/2-1(x)只是R1/2-2(x)的一种特例。

由于Pade逼近中采用了有理函数的最低阶数(M/N=1/2)，因此，(27)式不可能与tanh和gauss具有全局相同的性能。这就需要通过调整系数α和β的取值，使得通用函数R1/2-2(x)在一定范围内尽可能地逼近tanh(x)和gauss(x)，从而搜寻出R1/2-2(x)的极限性能。

由以上推导可知，tanh(x)和gauss(x)的幂级数是在x0=0处展开。因此，R1/2-2(x)的极限性能是在x0=0的一个邻域内，分别让R1/2-2(x)与tanh(x)，R1/2-2(x)与gauss(x)的曲线尽可能地相互重叠，并保证R1/2-2(x)与tanh(x)，R1/2-2(x)与gauss(x)具有相同的极大值和极小值。

在函数R1/2-2(x)两边分别对自变量x求导并令其为零，即

(28)

由(28)式可知，R1/2-2(x)在x=β1/2和x=-β1/2取得极值。再求二阶导数J(x)。

(29)

当x=β1/2时，J(x)<0;当x=-β1/2时，J(x)>0。因此，函数R1/2-2(x)在x=β1/2处取得其极大值，而在x=-β1/2处取得其极小值。

双曲正切函数f(x)=tanh(x)是奇函数，它的定义域为(-∞，∞)，其值域为[-1，1]。然而，当自变量x在有限值的范围内变化时，tanh(x)不可能取到数值±1，即函数tanh(x)是以f(x)=±1为渐近线，表示为

(30)

虽然x在有限值的范围内，函数tanh(x)不能达到其极限值±1，但仍然可以让函数tanh(x)尽可能地逼近其极限值。为此，分别取数值0.96(-0.96)，0.97(-0.97)，0.98(-0.98)和0.99(-0.99)作为tanh(x)的局部极大(极小)值;然后再根据这些极值计算出R1/2-2(x)中对应的待定常数α和β。通过比较不同极值情况下R1/2-2(x)与tanh(x)在x=0附近的曲线重合度来确定最优的极值。4种极值的波形如图1所示。

图1 4种极值对应的tanh(x)和R1/2-2(x)曲线Fig.1 Curves of tanh(x) and R1/2-2(x) corresponding to four extreme values

从图1可以看出，当取0.96(-0.96)作为tanh(x)的极大(极小)值时，R1/2-2(x)与tanh(x)在x=0附近的曲线重合度是最好的。

考虑到tanh(1.945 9)≈0.96和tanh(-1.945 9)≈-0.96，得β1/2=1.945 9和β≈3.786 5。将该β的值代入R1/2-2(x)表示式中有

(31)

因此解出α=3.736 1，并获得第2个替代tanh的有理非线性为

(32)

同样地，对于奇函数gauss(x)=x·exp(-x2/2)，它的极大(极小)值的点处于x=1(x=-1)处。因为gauss(1)=e-1/2≈0.606 5，gauss(-1)≈-0.606 5，可得β1/2=1和β=1，将该β值代入到表示式R1/2-2(x)中得到

(33)

即α=1.213 0，于是获得替代gauss的第2个有理非线性为

(34)

在实际应用中，用RVT-1，RVT-2替代tanh，用RVG-1，RVG-2替代gauss会产生误差。为了比较有理函数逼近经典非线性的性能，将函数的波形绘制在一起进行观察。6种非线性的曲线如图2所示。

图2 不同非线性的波形Fig.2 Waveforms of different nonlinearities

从图2a可以看出，在定义域中，函数RVT-1(x)，RVT-2(x)与tanh(x)的极值各不相同。当|x|>1时，随着|x|值的增加，这3种函数取值趋势的差别越来越大。然而，在|x|≤1的区间，3种函数曲线几乎完全重合，即在x=0的邻域用RVT-1和RVT-2替代tanh将不会产生明显的误差。

同样地，从图2b还可以看出，函数RVG-1(x)，RVG-2(x)与gauss(x)在|x|>1后取值趋势的差别也是越来越大。尽管RVG-2(x)与gauss(x)的极值几乎是相同的，但它们与RVG-1(x)的极值是不同的。若把自变量的值限制在x∈[-0.7，0.7]，则这3种函数的曲线几乎完全重叠。由于在Pade逼近中，仅考虑x=0邻域的麦克劳林级数，因此，有理函数RVG-1(x)和RVG-2(x)可以有效地替代经典非线性gauss(x)。

3 鲁棒性分析

由于观测向量x中每个信号的样本数是有限的，因此，ICA目标函数中理论的数学期望值实际上是用样本的平均值所代替。这就导致在信源的估计中产生误差，而渐近方差或协方差是该误差的经典度量。使ICA估计量渐近方差为最小的对比函数G(·)为[3-4]

Ggood(x)=c1logpi(x)+c2x2+c3

(35)

(35)式中：pi(x)是一个独立分量x的概率密度函数；c1，c2，c3是任意的常数。为简单起见，将常数项省略，则可以取

Ggood(x)=logpi(x)

(36)

从(36)式可知，对比函数实际上是类似于一种负熵的概念。

ICA估计量的另一个重要性质是对异常观测值的鲁棒性，即在观测数据中存在单个的很离谱的野值(outlier)对估计量的影响不大。鲁棒性同样取决于对比函数G(·)的选择。对于鲁棒性的估计量，则要求对比函数G(x)不能随着|x|的增长而快速增长[3]。

在BSS和ICA模型中，由于信源一般是服从非高斯分布的，因此，信源中的独立分量采用以下的概率密度函数族

pd(x)=C1exp(C2|x|d)

(37)

(37)式中：d是一个正的常数；C1，C2是归一化的常数，它们的作用是确保pd(x)成为一个单位方差的随机变量x的概率密度。对于不同的d值，(37)式中的概率密度反映出不同分布的信源。当02时，pd(x)则为亚高斯的概率密度。

综合考虑ICA估计量的渐近方差和鲁棒性这2种性质，即把(37)式代入到(36)式中，可得到最佳的对比函数形式。同样地，为简洁起见，在(37)式中的常数C1，C2也被省略，因此，对比函数为

Gopt(x)=|x|d

(38)

由于常数d取值是否为2可区分出独立分量服从的是高斯还是非高斯分布，于是将(38)式中的对比函数设定为平方函数|x|2。对于超高斯密度，最佳的对比函数是一个比|x|2增长慢的函数;而亚高斯密度的最佳对比函数是一个比|x|2增长快的函数。本文考虑的是超高斯音频信源，因而对比度函数应具有G(x)=|x|d(d<2)的形式。

为了分析有理非线性对ICA估计量渐近方差和鲁棒性的影响，把(27)式的R1/2-2(x)进行积分，得到对应的原函数(即对比函数)为

(39)

(39)式中的系数α和β分别用RVT-1，RVT-2，RVG-1和RVG-2表达式中的对应数值代入，则得到它们的对比函数分别为

(40)

(41)

(42)

(43)

为了分析有理非线性及其对比函数对信源的ICA估计性能(即渐近方差和鲁棒性)，将平方函数|x|2与GVT-1(x)，GVT-2(x)，GVG-1(x)和GVG-2(x)的曲线绘制在一起进行比较，其结果如图3所示。

图3 不同对比函数的波形Fig.3 Waveforms of different contrast functions

从图3可以看出，对比函数GVT-1(x)，GVT-2(x)，GVG-1(x)和GVG-2(x)的增长率都明显慢于二次函数|x|2。因此，应用有理非线性RVT-1(x)，RVT-2(x)，RVG-1(x)和RVG-2(x)的Fast-ICA算法所获得的ICA估计量不仅具有最小的渐近方差，而且对观测数据的异常值是鲁棒的。

另外，对于d<1的超高斯信源，由于函数|x|d的导数为分式且自变量x出现在分母上，于是对比度函数|x|d在x=0处是不可微的，即对|x|d的微分要进行近似处理。与|x|d不同，对比函数GVT-1(x)，GVT-2(x)，GVG-1(x)和GVG-2(x)在x=0处均是可微的，表明在Fast-ICA算法中使用本文提出的有理非线性将具有潜在的优势。

4 仿真及其结果分析

为了验证有理非线性的性能，将Fast-ICA中的经典非线性用本文的有理函数替代，通过仿真比较它们在BSS中的效果。为了获得公平的结论，各种非线性的仿真平台及条件是完全相同的。

4.1 仿真环境和性能指标

一般地，衡量ICA算法的性能包括2个方面[4]：①算法的统计性能，即对于未知信源的盲分离效果；②算法的计算负担，即执行算法需要的运行时间开销，也就是算法的收敛性能。

串音误差(cross-talk error)[16]是衡量ICA算法统计特性的重要指标，一般地将串音误差表示为

(44)

(44)式中：M是信源的数量；常数cij是矩阵C的元素。全局矩阵C=A·B，即A与B的点积，其中A为混合矩阵，B是由ICA估计出的解混合矩阵。串音误差PI的值越小，则ICA与BSS效果越好，反之亦然。

仿真硬件平台为笔记本电脑，操作系统为Windows10，CPU为Intel(R) Celeron(R) CPU 1007U @ 1.50 GHz，内存为4 GByte (RAM)。仿真软件为MATLAB 9 (R2016a)。用于测试的5个音乐音频信源(网址为http://www.freesound.org/)的类型为wav，信号抽样频率为44 100 Hz。每个信源的样本数量为N=216=65 536。5个信源s=[s1，s2，s3，s4，s5]T的波形如图4所示。

图4 5路音乐音频源信号的波形Fig.4 Waveforms of 5 audio music source signals

采用归一化峰度(normalized kurtosis)[4]值检验信源的分布

(45)

(45)式中：s是信源向量；ms为信源的样本均值。若k(s)=0，则信源s服从高斯分布;若k(s)<0，则s服从亚高斯分布;若k(s)>0，则s服从超高斯分布。对于图4中的5个音频信源s1，s2，s3，s4，s5，计算出它们对应的归一化峰度值分别为2.400 8，4.776 6，1.052 8，4.690 2，3.133 7。这些结果说明，所有信源都服从超高斯分布。

4.2 非线性本身的计算时间

为了比较不同非线性的计算时间开销，首先利用MATLAB命令x=randn(1，10^6)生成高斯分布测试数据，然后运行命令y=tanh(x)，z=x.*exp(-(x.^2)/2)，RVT-1(x)=2*x./(2+x.^2)，RVG-1(x)=3*x./(3+x.^2)，RVT-2(x)=(3.736 1*x)./(3.786 5+x.^2)，RVG-2(x)=(1.213 0*x)./(1+x.^2)，并记录各命令的运行时间。由于每次生成的测试数据都是随机的，因而在不同的仿真中，所得到的运行时间结果也是各不相同的。通过多次仿真实验，每次的运行时间数据基本都处于同样的范围之内。表1给出了其中的一次仿真运行结果。

从表1的数据可知，非线性tanh的运行时间是有理函数RVT-1的5.95倍，是RVT-2的6.16倍。同样地，非线性gauss的运行时间是RVG-1的4倍，是RVG-2的4.64倍。仅从非线性本身的运行时间来看，有理非线性要比相对应的经典非线性的计算速度快得多。

表1 各种非线性的运行时间

4.3 Fast-ICA算法的性能

对于不同非线性的Fast-ICA算法，主要比较它们对信源s的盲分离性能。仿真过程如下:首先产生代表采集信道特性的混合矩阵A;然后按照ICA模型由混合矩阵A和信源s获得观测信号x;最后利用不同非线性Fast-ICA算法估计解混合矩阵B并分离出信源。在仿真过程中，对Fast-ICA算法的运行时间和PI指标进行计算。

由MATLAB命令A=randn(5，5)随机生成的混合矩阵为

(46)

观测信号由模型x=As混合而成。对于5个混合信号x，利用不同非线性的Fast-ICA算法进行BSS。为了全面测试算法的整体性能，每种算法都进行了1 000次试验。图5给出了非线性tanh，RVT-1和RVT-2对应的Fast-ICA算法在1 000次实验中性能指标PI值的分布。

从图5中PI值的分布看，经典非线性tanh对应的Fast-ICA算法的盲分离性能从整体上比有理非线性RVT-1，RVT-2对应的Fast-ICA算法优一些。对于2种有理非线性来说，RVT-1的Fast-ICA算法比RVT-2对应算法的盲分离性能优一些。

图5 非线性tanh，RVT-1，RVT-2的Fast-ICA算法BSS性能Fig.5 BSS performance of Fast-ICA with tanh，RVT-1，RVT-2

然而，从图5的PI值分布只能给出3种非线性的Fast-ICA算法在盲分离性能方面总体上的粗略结论。为了从具体的PI值上进行相互比较，对于每种非线性的Fast-ICA算法，在仿真过程中还分别计算出它们在1 000次实验中最大(即最差)PI值、最小(即最优)PI值、PI值波动范围以及平均PI值。其结果如表2所示。

表2 tanh，RVT-1，RVT-2的Fast-ICA算法的PI值

从表2的数据可看出，在1 000次实验中，无论是PI的平均值、最大值、最小值，还是PI的波动值，经典非线性tanh的Fast-ICA算法都优于有理函数RVT-1和RVT-2的Fast-ICA算法。从平均PI值来看，tanh与RVT-2的差别体现在小数点后第3位上，而tanh与RVT-1的差别仅体现在小数点后第4位上，即这3种非线性对应的Fast-ICA算法对音频信号的盲分离性能没有实质性的差别。

同样地，图6给出了非线性gauss，RVG-1和RVG-2对应的Fast-ICA算法在1 000次实验中性指标PI值的分布。

图6 非线性gauss，RVG-1，RVG-2的Fast-ICA算法BSS性能Fig.6 BSS performance of Fast-ICA with gauss，RVG-1，RVG-2

从图6可以看出，有理非线性RVG-2的Fast-ICA算法比经典非线性gauss对应的算法具有更好的BSS性能;而且RVG-2的PI值更集中地分布在一个较小的范围内，这说明其BSS性能更加稳定。另外，经典非线性gauss的Fast-ICA算法比有理非线性RVG-1对应的算法具有更优的BSS性能，而且RVG-1对应的PI值分布范围很大。

为了从具体数值上比较非线性gauss，RVG-1和RVG-2的Fast-ICA算法的BSS性能，将在1 000次仿真中的最大PI值、最小PI值、平均PI值以及PI值的波动范围记录在表3中。

表3 gauss，RVG-1，RVG-2的Fast-ICA算法的PI值

从表3可以看出，无论是平均PI值、最大PI值、最小PI值，还是波动PI值，有理非线性RVG-2对应的Fast-ICA算法都明显要优于gauss和RVG-1对应的算法。从平均PI值看，gauss与RVG-1的差别体现在小数点后第4位上，而gauss与RVG-2的差别体现在小数点后第3位上。这说明，在Fast-ICA算法中用RVG-1代替gauss不会引起明显的BSS误差，而用RVG-2代替gauss会取得更好的BSS效果。

另外，通过比较图5与图6，以及表2与表3的PI值可以看出，非线性gauss，RVG-1和RVG-2的Fast-ICA算法比tanh，RVT-1和RVT-2对应的算法在BSS性能要好很多。这是因为tanh是一个通用的非线性，它对超高斯和亚高斯信源都是适应的;而gauss则是专门用于分离超高斯信源的，因此，对服从超高斯分布的音频信源具有更好的适应性。在实际的BSS应用中，由于信源是不可观测的，因而无法确定信源的分布。在这种情况下，非线性tanh及其有理函数RVT-1和RVT-2却可以实现混合非高斯信源的BSS，因此具有重要的应用意义。

为了比较不同非线性的Fast-ICA算法进行BSS所花费的运行时间(包括对算法saddle points的测试时间)，在1 000次实验中，分别记录了每种算法的最大(最差)运行时间、最小(最优)运行时间、运行时间的波动范围和平均的运行时间。其结果如表4所示。

从表4可以看出，有理非线性RVT-1和RVT-2的Fast-ICA算法各个运行时间指标都明显优于经典非线性tanh对应的算法。RVT-1的平均运行时间比tanh节约了0.065 9 s。将以上仿真重复100 000次，则总的运行时间将节约6 590 s，即109.83 min。对于RVT-2和tanh的Fast-ICA算法，RVT-2也可以节省大致相同的运行时间。

同样地，从表4还可以看出，RVG-1和RVG-2对应的Fast-ICA算法的运行时间指标也优于gauss对应的算法。RVG-2的平均运行时间比gauss节约了0.033 9 s。如果将以上仿真重复100 000次，则总的运行时间将节约3 390 s，即56.50 min。对于RVT-1和gauss的Fast-ICA算法，有理函数RVT-1还可以节省更多的运行时间。

表4 各种非线性的Fast-ICA运行时间

综合以上的仿真实验结果可知，虽然有理非线性RVT-1和RVT-2的Fast-ICA算法在BSS性能上略差于tanh对应的算法，但有理函数的快速计算能力却弥补了BSS性能的缺陷。对于超高斯的音频信源，有理函数RVG-1和RVG-2的Fast-ICA算法与gauss对应的算法具有几乎相同的BSS性能(而且RVG-2具有更好的BSS性能)，但在算法的收敛上，有理非线性RVG-1和RVG-2的快速计算能力却远远超过经典非线性gauss。从ICA算法的统计性能和收敛性能两方面看，有理非线性在大规模数据处理中具有潜在的优势。

5 结束语

在盲信源分离和独立分量分析的应用中，实时处理观测信号已成为普遍的现象，这就要求ICA算法具有更快的计算速度。为此，本文对Fast-ICA算法中的非线性进行有理化处理，以提高算法的计算效率。对于经典的非线性tanh和gauss，利用Pade逼近技术分别提出了2个有理多项式的非线性。为了进一步提高有理非线性对应Fast-ICA算法的收敛性能，由Pade逼近构造出的有理函数，其分子为简单的一次(线性)多项式，而分母也仅是二次多项式。

仿真结果表明，将经典非线性替换为有理函数的Fast-ICA算法具有更快的计算速度。同时，在盲信源分离的性能上，有理非线性与经典非线性具有几乎相同的效果。对于超高斯分布的音频信源，有理函数的Fast-ICA还可以获得更优秀的盲分离性能。