基于INSGA-II高维目标柔性作业车间调度的优化

李 丹，向凤红，毛剑琳

(昆明理工大学 信息工程与自动化学院，昆明 650500)

0 引 言

在当今市场激烈的竞争中，企业通过对生产调度进行改善以增加核心竞争。优化调度可以提高企业制造生产效率和利润率。柔性作业车间调度问题(flexible job shop scheduling problem,FJSP)是传统JSP的延伸，是数学上一类经典的NP-hard组合优化问题[1-5]。FJSP明显的优点是更加符合实际生产需求：机器可以通过合理利用空闲时间来节省闲置时间，从而提高设备的利用率；若在加工过程中碰到故障机器，工序可以绕过该机器选择其他继续加工从而维持生产的稳定；同一台机器上可以选择让同一个工件在满足工序可选该机器的前提下一直加工，减少了在不同机器上装卸的时间。

在实际复杂的车间生产调度中往往要考虑多项性能指标，即多目标优化问题，多个目标要同时得到满足且各个目标之间很可能相互冲突对立。当优化目标为4个或4个以上时，可以称之为高维目标优化[6]。一般企业的调度优化目标包括：最大化完工时间、瓶颈机器负荷、生产成本、平均流经时间、库存、总能耗、总拖期、总机器负荷等。通过大量文献研究可知，单一的算法由于算法的局部性使寻优过程中有很多不足，采用混合算法机制可以很好地提高算法的性能。郭钧等[7]研究了混合人工鱼群算法，针对不确定加工时间，考虑再制造技术的经济性和绿色性，采用种群协同进化的思想对算法进行改进来优化多个目标，对单种群和多种群进行了仿真结果对比，并验证了算法的有效性；裴小兵等[8]在遗传算法的基础上将博弈思想引入到多目标车间调度问题求解中，通过对3个目标之间的博弈策略实现优化组合解；孟冠军等[9]研究了各个阶段采取不同的新搜索机制的人工蜂群算法，与禁忌搜索算法相结合提高了局部搜索能力，通过大量算例仿真结果对比，验证了算法的优越性。帕累托最优解是满足多个目标的相对最优解，在工程学和经济学中得到广泛应用。为求解优化多目标问题，Srinivas等[10]在1994年设计了非支配解遗传算法(non-dominated sorting genetic algorithms，NSGA)；Deb等[11]在2002年提出了NSGA2，在NSGA的基础上加入了拥挤度计算、精英选择，很大程度上使计算复杂度降低；赵一霞[12]在NSGA2算法中采用循环计算拥挤度和改进精英选择策略，并通过多个案例证明了改进算法的有效性；张超勇等[13]针对NSGA2精英选择策略上的不足，采用层次分析法选择出最优Pareto解；陈辅斌等[14]研究了NSGA2算法，在选择操作中引入免疫自我调节功能，在精英保留策略中限制父代精英解的个数并适当增加非精英解的个数，提高了算法的优化性能；景志强等[15]研究了混合NSGA-II算法，在选择操作中对序值和拥挤距离使用模拟退火与模拟二进制相结合，并通过实验仿真证明了该算法具有更强的全局搜索能力。

本文针对车间调度生产中以完工时间、总拖期时长、机器负荷和生产总能耗为目标，对高维目标柔性作业车间调度问题(many-objective flexible job shop scheduling problem, MaOFJSP)进行了研究。在NSGA-II算法的精英选择策略上进行了改进，并根据优化目标的特点在变异操作中提出了基于改变关键工序块邻域结构的方法，最后通过Matlab模拟仿真，验证了算法设计和模型建立的可行性和有效性。

1 高维目标调度模型

1.1 问题的描述

高维目标调度问题可以描述为N个不同的工件在M台不同机器上加工，每一个工件有一道或多道工序，每一道工序都可在可选的机器集中任意选择一个加工。将工件的各个工序合理地分配给机器，使多个目标同时尽可能达到最优的加工序列为最优调度工序。

1.2 优化目标的分析

1)最大完工时间。在车间生产调度中加工工序和加工机器都满足的条件下，缩短工件Ji的最后一道工序的最大完工时间，可以使企业的生产效率得到很大的提高。随着效率的提高，车间生产就会按照规定的日期完工，不仅客户的满意度有所提高，而且可以通过减少工人的加班时间，降低生产成本。表示为

f1=max(Ci|i=1,2，…,n)

(1)

(1) 式中：Ci表示工件Ji最后一道工序的完工时间；n表示工件的个数。

2)总拖期时间。工件生产的超前完工会使库存资源浪费造成仓储成本的增加，推迟完工会给客户带来与期望相差很大的体验，从而降低客户满意度，同时受到合同协议的惩罚。在实际生产中为了保证高质量的产品，材料成本不能缩减，但可以减少成品仓储成本和违约成本。因此，最优的调度工序是总拖期时间接近于0。表示为

(2)

(2)式中，Di表示工件Ji的交货期。

3)机器总负荷。不同的调度方案，机器负荷的大小也不一样，机器总负荷越小，设备的利用率就会有很大提高。表示为

(3)

(3)式中：ni表示工件i的总工序数；pijk表示工件Ji的第j道工序在机器k上的加工时间；xijk是决策变量，若工件Ji的第j道工序在机器k上加工，则为1，否则为0。

4)总能耗。能耗包括机器加工能耗、机器空转能耗、车间工件转移能耗、车间固有能耗。减小总能耗可以提高生产的绿色性。表示为

γS+f1A

(4)

(4)式中：αk表示机器k上加工的平均单位能耗；Ck表示机器k的完工时间；βk表示机器k空转时的平均单位能耗；γ表示生产车间工件的转移能耗；S表示生产车间工件的转移次数；A表示生产车间的固定能耗。

1.3 约束条件

1)每个工件不同工序之间的先后顺序约束，表示为

Sij+pijkxijk≤Cij

Cij≤Si(j+1)

(5)

(5)式中：Sij表示工件Ji的第j道工序的加工时间；Pijkxijk表示该道工序在机器k上的加工时间；Cij表示该道工序的完工时间；Si(j+1)表示该工件下一道工序的开始时间。

2)每个工件的完工时间不能超过最大完工时间，表示为

Ci≤Cmax

(6)

3)每道工序只能在可选的机器集中选择一台机器进行加工，表示为

(7)

(7)式中，Mij表示工件Ji的第j道工序可选的机器集。

4)同一个时刻同一台机器上只能加工一个工序，表示为

Sij+pijk≤Sgh+L(1-yijghk)

Cij≤Si(j+1)+L(1-yi(j+1)ghk)

(8)

(8)式中：Sgh表示工件Jg的第h道工序；L表示一个很大正整数；yijghk表示若Oijk先于Oghk为1，否则为0。

5)每一台机器在满足工序可选机器集的条件下可以循环在一台机器上操作，表示为

(9)

2 改进NSGA-II(INSGA-II)算法设计

2.1 染色体编码和解码

根据柔性作业车间调度复杂性的特点，染色体编码采用基于工序排序和机器选择的双层编码。随机生成一组有效的工序编码，找出工件i在工序染色体中对应的序号，基于工序编码在可选的机器集中随机选择2个机器，通过随机生成0～1的任意值来判断具体选择哪个机器进行加工，若此值>0.8，则在随机生成的2个机器中选择加工时间短的，若此值≤0.8，则选择另一台机器。基因由2部分组成，前半部分为工件的加工顺序，每一个相同的数字代表同一个工件，出现的次数代表这个工件的第几道工序；后半部分为机器编码，每一个数字代表前半部分工件加工工序依次选择的机器编号,如基因串[31212231132322],工件的加工工序为O31O11O21O12O22O23O32，依次对应的加工机器为1132322。解码是把染色体解码成可行的调度工序，从染色体前半部分依次记录当前解码过程中工序在序列上顺序，将工件的每一道工序安排到尽可能早的时刻进行加工的机器上。从染色体后半部分依次记录当前解码过程中该道工序在该机器中待加工序号，记录所有机器的加工间隙，然后基于工件和加工机器的约束，来判断最终约束。

2.2 Pareto排序

随着目标函数的增多，Pareto排序可以大大提高运行效率。种群初始化选择每一个个体X依次与剩余个体比较，若X的目标函数值优于Y个体的目标函数值(即X支配Y)，则把Y放入集合SX中(即所有被X支配的个体都放入SX)。在X依次与个体比较过程中，若有个体支配X，则支配X的个体数量加1(nX代表支配X的个体数量，即nX=nX+1)，把nX为0的所有个体X放入第1层，即非支配等级1。将等级1层作为当前层并找出该层中每一个个体的SX集合，把SX中每个个体的nX减1(nX=nX-1)，把nX为0时的所有个体放入第2层，即非支配等级2。重复以上操作，直到每一个个体都被分配对应的等级为止。

2.3 精英选择策略

传统的精英选择策略是把Pareto排序等级低的个体留下，其余去掉，这样就会造成选择操作中全是精英解而形成局部最优的情况。可以在父代种群中适当加入一些非精英解确保解的均匀分布，这样就保证了种群的多样性。非精英解是Ai中前ni个个体，计算公式为

ni=|Ai|×λi

(10)

(10)式中：ni为第i层非支配曲面Ai上选取的个体数量；|Ai|为非支配曲面上的个体数量；λi为(0,1)的常数。

在精英选择过程中，当非支配解等级一样时，可以优先选择拥挤度大的个体。拥挤度的大小是由同一个层的非支配解中个体的拥挤度与相邻2个个体的目标函数值之差判断的。如个体A与相邻2个个体围成的区域内的其他个体的拥挤度大小一样，且都可以被A支配，就无法判断A和被围成区域内的个体哪个才是最优。为保证个体A能够顺利被选择到父代种群，引入了改进的选择策略，步骤如下。

步骤1根据不同目标函数值的大小进行降序处理。

步骤2把进行降序处理的个体分成一定规模的种群。

步骤3计算各个规模种群中每个个体的斜率ki，计算式为

ki=(f1(i)-f1(i+1))/(f2(i)-f2(i+1))

(11)

(11)式中：f1，f2表示个体二维方向的2个目标函数值；i=1,2,3,…,n-1，其中，n为全部个体的数量，当i=n时，个体斜率趋近于负无穷。

步骤4将每个种群中斜率最小的个体选择进入父代，其余个体全部放入一个种群中，通过锦标赛选择法进入父代。

2.4 交叉操作

交叉操作对遗传算法全局搜索能力有着很大的影响，柔性作业车间调度的交叉操作为基于工序排序部分的交叉和机器选择部分的交叉。①工序交叉：将工件随机分成2个不同的集合A和B，从第2代父代个体中随机选择染色体a和b，将父代染色体a中A的工件按位置不变的顺序复制到子代染色体a1；同理，将父代染色体b中B的工件按位置不变的顺序复制到子代染色体b1。将父代染色体a中剩余工件，即A中的工件按顺序复制到子代b1；同理，将父代染色体b中剩余工件，即B中的工件按顺序复制到子代a1。工序交叉如图1所示，a和b这2个染色体有5个工件，将工件1和工件3(图1中阴影部分)放入集合A中，将染色体a中的工件1和工件3复制到a1中，将染色体b中的工件1和工件3去掉，其余按顺序复制到a1。②机器交叉：从第2代父代个体中随机选择染色体a和b，将染色体a和b中分别随机选择2个位置的基因按位置顺序不变复制到子代染色体a1和b1中；将父代染色体a中剩余的基因按顺序复制到子代b1中，将父代染色体b中剩余的基因按顺序复制到子代a1中。机器交叉如图2所示，随机选择染色体a中1，2和b中2，3的2个位置分别复制到子代染色体a1和b1中，将染色体a中剩余的基因4，2，4和染色体b中剩余的基因5，2，3按顺序分别复制到子代染色体b1和a1中。

图1 工序交叉Fig.1 Process cross

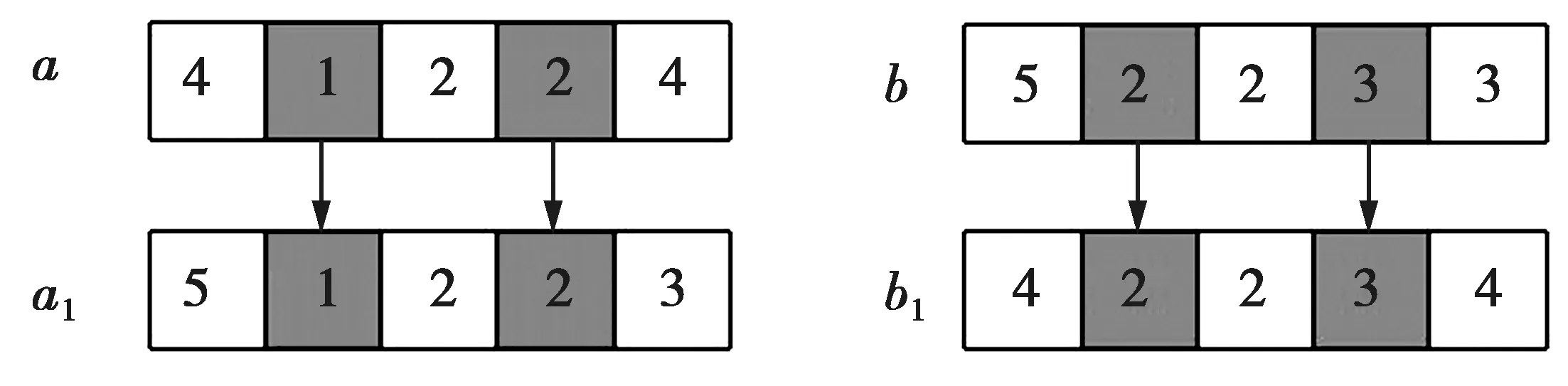
图2 机器交叉Fig.2 Machine cross

2.5 变异操作

变异操作对遗传算法局部搜索能力有着很大的影响，一个设计合理且具有指导意义的邻域结构对局部搜索能力有着至关重要的作用。根据目标函数确定块结构邻域的性质，去除非优质解，在剩余的优质解集中进行搜索可以提高效率。目前相关研究是将一个块内关键工序的块首块尾互换、相邻块结构互换、块内移到块首或块尾等。关键路径是指加工过程中在同一台机器上加工工件相邻的关键工序。根据甘特图上的块结构邻域可以发现，改变一条关键路径的非公共部分的邻域结构不会影响另一条关键路径，就不会改变问题目标。在同一台机器上的不同工件(或同一工件)的不同工序之间，通过对相邻块结构采用插入或互换操作，选择让工序小的先加工，可以很大程度上减小最大完工时间。过程如下：①基于工序的变异，首先确定要变异的工序和机器，记录工件J的所有位置，在变异工件的全部工序中找到最大工序所在位置以及工件的上一个工序所在位置，允许变异将工序小的插入到工序大的前面；②基于机器的变异，记录每个机器上各有几个加工工序，找出工序最多的机器及确定需要变异的位置，根据各机器的加工工序数目生成变异的概率，将工序多的向工序少的变异。

3 仿真和分析

本文将传统NSGA-II算法和INSGA-II算法进行了对比分析，以8个工件在8台机器上加工为例进行了Matlab模拟仿真，如表1所示。图3和图4分别是传统算法和改进后算法仿真车间调度甘特图，根据颜色的不同来区分工件的编号，在小矩形方框中P(X,Y)=A，等号左边代表工序，其中，X是工件的编号，Y是工件X的第Y道工序，等号右边是工件X的第Y道工序在机器(纵坐标对应的数字代表机器编号)上的加工时间。从图3，图4可以看出，在相同条件下，算法改进前后的4个目标函数值分别为(93，6，377，181.68)和(68，0，363，160.15)，对比发现改进后算法结果更优。

表1 8×8实例

图3 传统NSGA-II的甘特图Fig.3 Gantt chart of traditional NSGA-II

图4 INSGA-II的甘特图Fig.4 Gantt chart of INSGA-II

图5为4个目标最优解空间分布对比图，星星图案代表传统NSGA-II算法的解，圆形图案代表INSGA-II算法的解，不同颜色表示机器总负荷的大小，可以明显看出，改进后的Pareto解优于传统算法。

表2为10个工件、8台机器的FJSP算例，对比了3种算法，在最大完工时间方面，INSGA-II明显优于多目标遗传算法(multi objective genetic algorithm,MOGA)和传统NSGA-II；在总拖期时长方面，INSGA-II和MOGA结果相似，均优于传统NSGA-II；在机器总负荷方面，INSGA-II略优于其他2种算法；在总能耗方面，INSGA-II优于MOGA，MOGA优于传统NSGA-II。有效验证了该算法的稳定性和求解高维目标FJSP的有效性。

表2 10×8实例

图5 Pareto最优解分布对比Fig.5 Pareto optimal solution distribution comparison

4 结束语

柔性作业车间调度是一个复杂的生产系统。实际生产调度过程中，机器故障、订单取消、新订单加入等动态事件的出现会使工况发生变化，可能导致既定调度方案变得不再可行。因此，调度方案的动态优化十分重要。本文研究了多目标优化求解柔性作业车间调度问题，提出改进非支配解遗传算法来实现优化指标。通过Matlab模拟仿真，验证了算法设计和模型建立的可行性和有效性。科技的飞速发展对动态车间调度提出了更高要求，但目前有关此课题的研究仍较少见，未来尚有较大的提升空间。