自适应OFDM调制结构优化设计

2022-05-03王光宇陈峻嵩

重庆邮电大学学报(自然科学版) 2022年2期

梁燕，李倩,2，王光宇,2，邵凯,2，陈峻嵩

(1.重庆邮电大学通信与信息工程学院，重庆 400065；2.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065)

0 引言

第五代移动通信系统(the 5th generation mobile networks，5G)要求支持异构的服务，包括增强型移动宽带(enhanced mobile broadband,EMB)、大规模机器类型通信(massive machine-type communications, MMC)和超可靠低延迟通信(ultra-reliable low-latency communications, URLC)等。根据业务的需求多样性，接入无线网络(radio access network, RAN)以网络切片技术提供物理资源配置。例如，低数据流通信分配少数目的子载波，实时医疗通信满足低时延配置等。这对物理传输波形设计提出了非常灵活的要求。

5G研究中提出了几种候选波形，包括基于正交频分复用(orthogonal frequency division multiplexing，OFDM)的滤波OFDM(filter OFDM,F-OFDM)、加窗OFDM(window OFDM,W-OFDM)、通用滤波多载波(universal filtered multi-carrier, UFMC)以及滤波器组多载波(filter-band multi-carrier, FBMC)等。同时，为了配合波形设计的灵活性，提出了一种参数集numerologies，可以为不同业务适配传输帧[1]。F-OFDM是利用滤波实现的一种频谱整型机制，能够避免一定的带外泄露(out of band emission, OBE)，且其将带宽划分成子带，通过numerologies配置可提供一定的灵活性[2]。但F-OFDM是对数据流进行全带滤波，这导致了滤波器的长度过长，系统复杂度变高[3]。W-OFDM则保留了OFDM的核心接收机结构，与滤波型技术相比其具有相对简单的加窗频谱约束，且峰均功率比(peak-to-average-power ratio, PAPR)比较低[4]，然而在高信噪比下，频谱效率及鲁棒性能低[5]。由于引进了numerologies，5G新波形在边缘子载波容易产生不同numerologies之间的干扰(inter numerology interference, INI)[6]。INI严重影响不同用户之间的波形共存，文献[7]中提出了一种INI分析模型，该模型将INI分为等效噪声部分和显性确定部分，然后再用干扰消除算法进一步处理。

在第六代移动通信系统(the 6th gen-eration mobile networks，6G)中，通信系统对于5G的三大应用场景要求更高。例如，EMB频谱更宽速度更快，在紧急情况下支持URC用户海量连接更加灵活[8]，业务直接切换更加频繁。这对底层波形设计提出了更高的时变性要求，即时/频资源配置更快更灵活。5G研究中的波形设计，更多考虑的是OBE与INI消除问题，对业务转换的时变特性还没有涉及。例如，F-OFDM能够针对不同用户分配不同时间/频率长度的资源块，然而在时域上，当用户切换业务时却难以做到无缝连接，无法自适应调节参数以满足用户灵活切换业务的需求。

5G中对FBMC有较深入的研究，但很多文献中提到的FBMC实际特指偏置正交负端调制滤波器组多载波(filter bank multicarrier on offset-quadrature amplitude modulation, FBMC/OQAM)。调制滤波器组被广泛应用于数据压缩、特征检测提取以及多载波调制等信号处理中。目前调制滤波器组分为离散傅里叶变换(discrete Fourier transform，DFT)滤波器组和离散余弦变换(discrete cosine transform, DCT)滤波器组。DFT滤波器组有FBMC/OQAM、滤波多音调制等特殊结构，由于DFT是一种复数调制，其固有干扰始终无法彻底消除，故很难满足滤波器组的完全重建。而DCT为实数调制，在通信信息传输中可以达到完全重建。DCT滤波器组实现简单且设计成本低，具有更出色的频谱压缩和能量集中特性，因此在基于插值的信道估计中具有更好表现[9]。

在6G中，mmWave和太赫兹的应用使频谱资源不再受限，DCT滤波器组应用障碍不复存在，而某些特殊应用场景，如MMC无人机通信、URC灾难应急处理等，将对通信设备的更快更灵活接入提出更高要求。因此，本文提出了一种基于离散余弦变换的自适应OFDM(adaptive OFDM， AOFDM)调制结构。首先，采用DCT滤波器组完成子载波级的滤波整型，有更好的频谱收敛特性，利于抑制OBE和INI；其次，可根据numerologies完成不同业务的初始参数配置，保留5G中各候选波形的灵活优势；再次，采用原型函数图形法[10]分段配置原型函数，完成AOFDM的收发信号在变化状态下的完全重建，即当用户业务发生切换时，自适应调整滤波器组设计参数以达到不同业务的无缝切换，不影响当前传输连接；最后，继承了DCT滤波器组的抗频偏特性和完全重建特性[11]，在理想信道条件下可达到无误码率传输，即使是衰落信道，也能表现出良好的传输性能。综上，AOFDM继承了DCT滤波器组的已有优势，并增加了时变特性。本文重点在于讨论其变化状态时的完全重建特性。

1 系统模型

相较于传统调制结构，AOFDM有多个随时间m变化的可调参数，如图1所示。

在逆离散余弦变换(inverse discrete cosine transform, IDCT)及DCT滤波器组中

hd(n,m)=gd(-n,m)=h(n,m)×

(1)

(1)式中：hd(n,m)和gd(n,m)分别为IDCT和DCT滤波器组系数，hd(n,m)={h0(n,m),h1(n,m),…,hM(m)-1(n,m)}，gd(n,m)={g0(n,m),g1(n,m),…,gM(m)-1(n,m)}；M(m)为滤波器重叠系数；0≤d≤M(m)-1；0≤n≤L(m)-1； 0≤k≤M(m)-1。

图1 自适应OFDM调制结构框图Fig.1 Block diagram of adaptive OFDM modulation structure

用户原始数据流在发送端经过串并转换以及基带调制得到复数信号xd(n,m)={x0(n,m),x1(n,m),…,xM(m)-1(n,m)}，然后经过M(m)倍上采样，通过发送端IDCT滤波器组对信号进行子载波级整形调制得到发送信号。接收端对信号进行DCT滤波处理得到yd(n,m)={y0(n,m),y1(n,m),…,yM(m)-1(n,m)}，最后通过均衡解调恢复出原始发送信号。表1给出了AOFDM中时间m相关参数，AOFDM的时变特性主要体现于对这些参数的灵活配置。

表1 AOFDM中时间m相关参数

根据滤波器组理论，DCT滤波器组系数矩阵应为IDCT滤波器组系数矩阵的转置。要保证IDCT与DCT变化后信号的完全重建，需要满足的完全重建条件为[12]

N(m)-1+i]=

(2)

(2)式中：hi(n,m)为滤波器组系数矩阵；IM(m)为单位矩阵。

2 自适应处理机制

本文提出的AOFDM，为多业务系统提供了一种更加灵活的调制结构。当用户业务所需数据流发生改变时，该调制结构能够自适应地调节分配的子载波数目以更好地为用户服务；当用户业务时延需求发生改变时，该调制结构同样能够自适应调节滤波器的重叠系数以达到所需时延。根据滤波器组长度L(m)=K(m)M(m)，子载波数目的改变以及滤波器重叠系数的改变均可视为滤波器长度发生改变，因此，可以利用滤波器原型函数的改变来达到用户需求。要完成AOFDM的时变处理，在用户业务切换时刻不影响系统传输性能，重点是保证变换前、变换过程中及变换后滤波器组的完全重建。

2.1 子载波数目改变

当用户的业务数据流减小时，为了节约频谱资源，可以降低传输该信息的子载波个数。通过减小上下采样倍数即减少子载波数目。本节以M(m)个子载波长度为L(m)=2M(m)的滤波器组转换成一个M(m)/2个子载波长度为L(m+1)=2M(m+1)=M(m)的滤波器组为例。为了保证在减少子载波数目的同时不增加误码率，需要变换前后滤波器组近似完全重建。可通过组合业务切换前后滤波器组的原型函数图形，使系统在调整子载波数目过程中仍然保持最佳性能。

发送端长度为L(m)=2M(m)的滤波器满足完全重建的原型函数为

(3)

(3)式中，0≤n≤2M(m)-1。

调整子载波数目实质上就是M(m)的值改变，因变换前后的滤波器原型函数表达式基本不变，简单来说就是对原型函数进行相应压缩。假设在m时刻及以前时刻为8个子载波即M(m)=8，在m+1时刻子载波数目减半为4，则变化前后时刻的原型函数如图2所示。

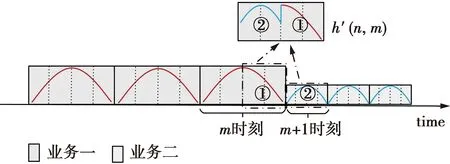
图2 子载波数减半的原型函数图形Fig.2 Prototype function graph of the half-number of subcarriers

前一时刻函数的后半部分和当前时刻函数的前半部分对称，即原型函数满足时变对称，才可能构成滤波器组的完全重建条件。图2中，m时刻的原型函数和m+1时刻的原型函数不是时变对称的，且此种情况下K(m)恒等于2，故恢复m时刻发送的信号所使用的实际原型函数h′(n,m)为m时刻的原型函数后M(m)长度与m+1时刻的原型函数前M(m)长度相拼接，即h′(n,m)由①、②段拼接而成。其他时刻原型函数均满足时变对称，所以只需要关注h′(n,m)是否对称即可，而拼接的h′(n,m)并不对称，因此，保证完全重建需要对原型函数进行适当修改，同时应满足

h2(n+M(m),m)+h2(n,m+1)=1

(4)

(4)式中，0≤n≤M(m)-1。

为减小复杂度，调整m时刻原型函数的后半部分，与m+1时刻的前半部分时变对称。调整后的原型函数如图3所示。

图3 m时刻原型函数h(n,m)的构造Fig.3 Construction of prototype function h(n,m) at time m

将m时刻原型函数h(n,m)的后半部分分为3段。第1段为1，长度为m时刻与m+1时刻的子载波数目差值的一半；第2段与h(n,m+1)的前半部分对称，长度为m+1时刻的子载波数目；第3段为0，长度与第一段相同。为了和h(n,m)的后半部分对称，把h(n,m+1)移位m时刻原型函数为1的长度。如此，既保证了h′(n,m)的对称，又保证了(4)式的成立。同时，由于h(n,m+1)进行了位移，h′(n,m)的拼接还需要m+2时刻的前M(m)/4=M(m+1)/2长度。h′(n,m)中有置为0的部分，该部分可与任何部分对称。子载波数目改变前后时刻的原型函数如图4所示。

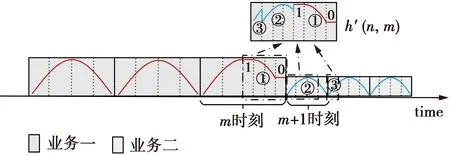
图4 子载波数减半且完全重建的原型函数图形Fig.4 Prototype function graph with the number of subcarriers halved and completely reconstructed

通过调整后，m+1时刻的原型函数为

(5)

(5)式中，0≤n≤2M(m+1)-1。

对比(3)式和(5)式可得，用户业务切换前后，所改变的只有子载波的数目。从m+1时刻开始，用户所分配的子载波数目为4个，满足用户服务的同时，节约了频谱资源。

当用户需要的数据流增大时，应增加子载波数目，该调整可以看作是对滤波器原型函数进行了扩展。假设在m时刻及以前时刻为4个子载波即M(m)=4，在m+1时刻子载波数目倍增到8，其转换前后时刻原型函数如图5所示。

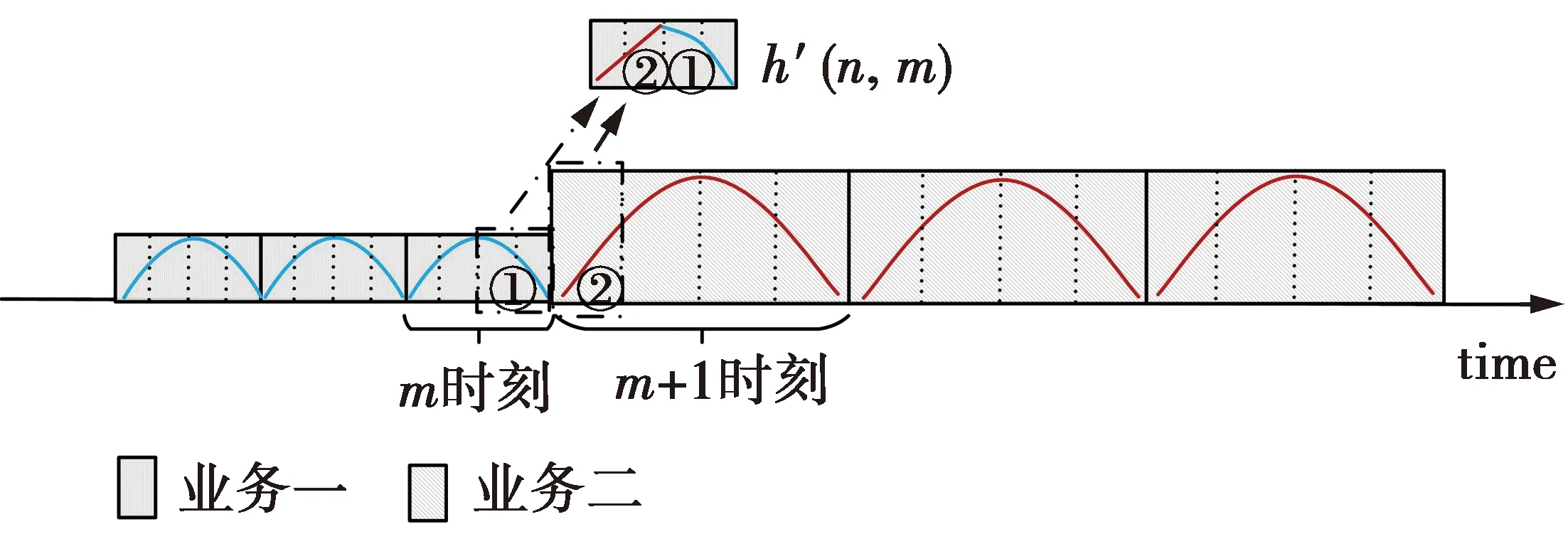
图5 子载波数增倍的原型函数图形Fig.5 Prototype function graph with doubled subcarrier number

显然图5不满足时变对称条件，同样需要部分调整原型函数。由于m+1时刻的原型函数比m时刻长，因此调整m+1时刻原型函数的前半部分，以便和m时刻原型函数的后半部分对称，从而达到完全重建条件。转换前后时刻原型函数如图6所示。

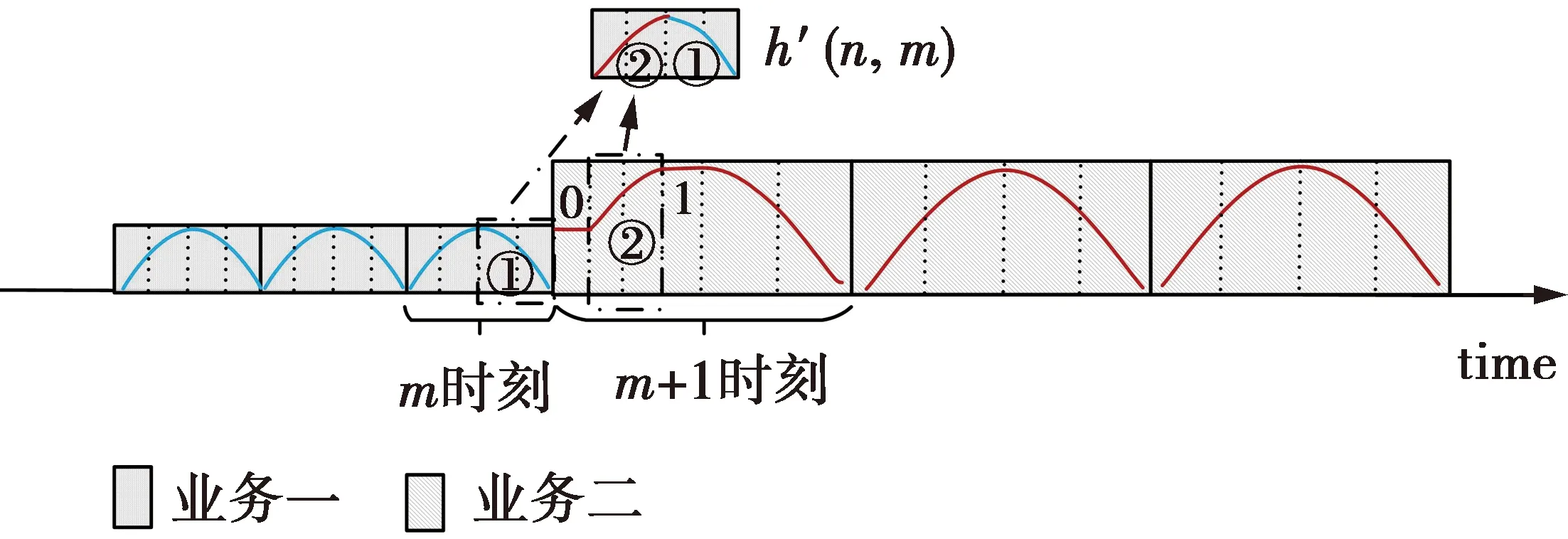
图6 子载波数增倍且完全重建的原型函数图形Fig.6 Prototype function graph with doubled number of subcarriers and completely reconstructed

为满足重建条件，对m+1时刻的原型函数进行位移。因此，在h′(n,m)的拼接中即图6②段的选取也进行相应位移。在m+1时刻用户切换业务，到下一次用户切换业务之前，分配的子载波均为8，即上下采样器的倍数均为8。如此，在保证数据传输不间断且没有增加误码率的情况下，完成了用户的需求数据流增大业务切换。

2.2 时延改变

当转换后的业务要求时延更低时，由于滤波器组长度越长时延越高，因此，通过减小滤波器组的长度来降低时延。本节以滤波器组长度从4M(m)转换到2M(m+4)为例。在这种情况下，用户所分配的子载波数量不改变，即上下采样倍数恒等于M。m时刻，该滤波器的原型函数为

(6)

(6)式中，0≤n≤4M-1。

一般情况下，滤波器组的长度越长，需要部分调整原型函数的时刻就越多，即过渡区越长。此时，需要部分调整4个时刻的原型函数，才能在不破坏系统传输性能的情况下从长度4M的滤波器组过渡到长度为2M的滤波器组。恢复m时刻发送的信号即业务一的最后一个信号所使用的实际原型函数h′(n,m)由①、②、③以及④段拼接而成，而恢复m+4时刻发送的信号即业务二的第一个信号所使用的实际原型函数h′(n,m+4)由⑤、⑥段拼接而成。假设M=8，时延改变前后时刻原型函数如图7所示。

图7 时延改变且完全重建的原型函数图形(L(m)=4M,L(m+4)=2M)Fig.7 Prototype function graph with time delay changed and completely reconstructed (L(m)=4M,L(m+4)=2M)

在图7中，从m+1时刻开始，滤波器的原型函数开始调整。m+1时刻到m+3时刻为过渡区，原型函数的构建原则是拼接出对称的h′(n,m)保证m时刻系统的传输性能不受业务切换的影响。实际上，业务切换发生在m+4时刻，此时发送的第一个信号也能完全重建，即h′(n,m+4)对称。而m+5时刻滤波器组完全过渡到长度为2M的滤波器组。用户业务切换之后，滤波器的长度减半，时延也将减小且不增加误码率，从而达到了用户切换业务之后的时延要求。

3 仿真及结果分析

表2列出了仿真参数。

图8为OFDM与AOFDM在QPSK与16QAM时的PAPR仿真对比图。AOFDM继承了DCT变化的优点，无论采用QPSK还是16QAM，其PAPR性能都明显优于OFDM系统。图8中，L=2M和M=128分别表示AOFDM时延减小和子载波数目减半后的情况。当子载波数目从256调整为128后，AOFDM的PAPR性能有所提升，这与载波数减少有关；而调整时延前后，滤波器长度从4M变为2M，AOFDM PAPR性能无明显变化，说明PAPR性能与时延大小弱相关。

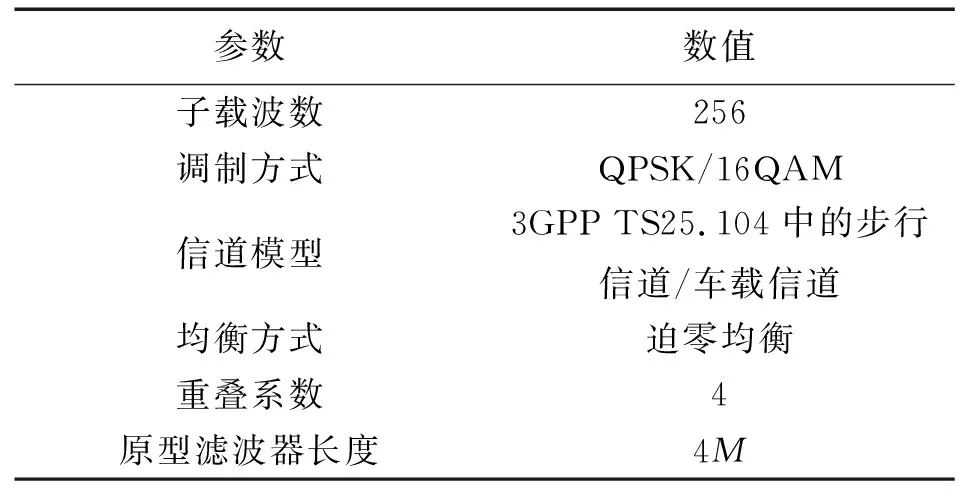
表2 仿真参数

图8 不同基带调制下系统PAPR性能比较Fig.8 Comparison of PAPR performance of the system under different baseband modulation

图9为采用QPSK调制时系统的BER仿真对比图。仿真结果表明，无论在步行信道还是车载信道，AOFDM的BER性能相比于OFDM系统均无明显损失。而在时变调整后，即图9中L=2M和M=128的情况，AOFDM的误码率与调整前也无明显损失。这符合AOFDM时变调整前后时刻需要保证的完全重建特性。

图10显示时延调整实例在原型函数长度从4M(m)转换到2M(m+4)时频谱变化过程。图10a为变化前m时刻原型函数频谱图，满足完全重建特性；图10b—图10d为m+1时刻到m+3时刻原型函数自适应变化频谱图，在不暂停信息传输的同时，为m+4时刻的业务切换做准备；图10e为业务切换m+4时刻原型函数频谱图；图10f为m+5时刻已完成切换的完全重建原型函数频谱图，此时的调制结构已经结束自适应调节。切换过程各个时刻仍能满足系统的频域收敛特性，不会带来额外的带外干扰，保证了信息传输。

在OFDM系统中，M点快速傅里叶变换的实数乘数目为MlbM。AOFDM中，由于采用子载波滤波器，复杂度要比OFDM高，工程中常利用多相分量矩阵实现[12]。该结构大大减少了所需运算的数量，尤其是乘法数量。当DCT滤波器组的长度为L=NM时，本文提出的AOFDM调制结构实数乘法计算次数为(M/2)lbM+2M+NM。

4 结论

未来移动通信具有更复杂的业务形态，接入无线网将以网络切片形式提供物理资源的灵活配置。本文针对未来网络的灵活需求，提出了AOFDM调制结构。首先，AOFDM继承了DCT变换完全重建的特性，并且具有很好的PAPR性能及频谱收敛特性，适合多载波传输机制，能较好地抑制OBE和INI；其次，AOFDM具有自适应调节特性，可以满足5G中numerologies配置要求，并能保证海量业务快速灵活无缝切换；最后，AOFDM结构继承了OFDM系统在应用时的自适应调制优点。需要强调的是，AOFDM有较好的频谱收敛特性，在对子信道的选择性利用上更具优势。但是，DCT调制采用实数调制而导致频谱利用率低的问题，这对未来AOFDM的应用提出了重要的讨论课题。综合来看，在某些特殊应用场景，如MMC无人机通信、URC灾难应急处理等领域，AOFDM是值得考虑的备选方案。