一种具有抗噪声能力的图像清晰度评价函数

林 丽，李诗云，陈 健

(福建工程学院 电子电气与物理学院，福州 350118)

0 引 言

随着工业生产自动化程度的不断提高，机器视觉技术在精密加工过程中的应用也越来越广泛。在机器视觉和图像测量领域中，自动对焦技术是获取清晰图像的前提。基于图像处理技术的被动式对焦方式具有成本低、功耗小、算法灵活、容易控制等优点[1]。被动式对焦又分为对焦深度法和离焦深度法两类，由于对焦深度法利用了计算机处理数字信号的高速性和灵活性，在工业应用中具有适应面广、改进潜力大等特点[2]，受到了国内外研究者的普遍关注。

在对焦深度法中，涉及到3个关键技术：对焦窗口选择、图像清晰度评价函数和搜索算法[3]。1993年，Subbarao等[4]为清晰度评价函数研究奠定了理论基础。近年来，许多学者对清晰度评价函数和对焦窗口选择方法进行了研究。针对清晰度评价函数，Murat[5]提出了一种利用彩色图像R，G，B这3个分量中亮度最大分量的对比度进行评价的方法，有效提高了对焦精度；Zou等[6]利用傅里叶变换计算信号频谱作为评价函数；Roh等[7]提出了模糊划分和模糊变换对方差进行改进的评价方法；刘书炘等[8]提出了一种基于改良Canny算子的清晰度评价函数，该方法利用模糊熵来确定边缘点的高低阈值，从而实现Canny算子的自适应边缘检测，具有良好的实时性、准确性和抗干扰性；张丰收等[9]提出了将4方向的Sobel梯度函数和Brenner梯度函数相乘作为清晰度评价依据，获得了清晰度更高的细胞显微图像；王烨茹等[10]针对夜景等应用场景，提出一种去除饱和像素的评价函数，可用于含有光源等过亮区域场景的拍摄；李成超等[11]针对微小零件显微图像的纹理具有相似性，边缘信息太少的问题，提出了一种基于局域方差信息熵的清晰度评价算法，该方法同时考虑了灰度的概率信息和图像的空间信息，具有较高的灵敏度以及较好的抗噪性；针对对焦窗口选择，刘威等[3]为解决固定窗口中图像目标不在选择区域的问题，提出一种自适应的窗口动态选择方法，提高了对焦的准确性；江旻珊等[12]克服了传统窗口选择方法的弊端，提出了一种基于改进的人工鱼群算法的窗口选择方法，该方法具有良好的稳定性；吴迪等[13]提出一种用于数码相机自动对焦过程的窗口选择方法，该方法中对焦窗口可以随着镜头位置调整。

通常一幅图像包含有大量不同尺度的信息，而图像的研究往往仅限于某一尺度或某些尺度上，因此，将图像按尺度进行分离十分必要，这样既可以消除其他尺度信息对图像处理结果的影响，也可以简化图像处理的难度和复杂度[14-16]。常用的多尺度分析方法有小波变换和希尔伯特-黄变换(Hilbert-Huang transform，HHT)。HHT信号分析方法是由美国航空暨太空总署哥达德太空飞行中心的华裔工程师Huang等[17]于1998年提出的，它通过经验模态分解(empirical mode decomposition，EMD)将信号中真实存在的不同尺度波动或趋势逐级分解出来，产生一系列具有不同特征尺度的数据序列，其中每一个序列称为一个固有模态函数(intrinsic mode function，IMF)。小波分解的基函数是预先确定的，采用不同的小波基，分析结果有很大的差异。而HHT对于不同信号，分解的基函数是从信号中自适应得到，可以说它是一种自适应的广义基[18]。将二维经验模态分解(bidimensional empirical mode decomposition，BEMD)方法与图像处理技术结合，已经成为不少学者研究的方向[19-23]。

基于以上分析，本文提出一种结合4方向Scharr算子、BEMD及能量梯度函数的自动对焦方法，方法首先利用4方向Scharr算子进行多区域窗口选择以提高算法的实时性，再通过BEMD提取对焦窗口中的不同尺度信息，最后由最高2个尺度分量加权并结合能量梯度函数，计算最终的清晰度评价函数值。由于减小了最小尺度的信息，因此，方法获得了较好的抗噪性能。同时，本文针对用于精细对焦阶段的清晰度评价函数，提出累加差值这一评价指标来定量分析清晰度评价函数峰值附近的灵敏度。实验表明，本文算法具有较好的实时性、抗噪性能以及灵敏度。

1 二维经验模态分解

1.1 二维经验模态分解原理

自然图像具备多尺度特性，利用HHT的自适应多分辨特性，将一维信号处理的方法推广到二维，可以将图像按尺度从小到大进行分离，小尺度信息包含了图像的细节，剩余的大尺度信息表达了图像的基本趋势和结构。

BEMD方法是由Nunes等[24]提出的。以灰度图像为例，可以将一幅灰度图像考虑为一个矩阵，其行列坐标表示图像中的一个点，而矩阵中相应元素的值则表示该点的灰度值。根据图像的实际尺寸定标图像所在平面(oxy坐标平面)的坐标，图像对应像素的灰度值设定为Z坐标，将图像的Z坐标垂直投影到oxy坐标平面即可表示一幅灰度图像。

按照EMD的方法，进行BEMD分解，首先在投影面上进行局部极值点选取(包括极大值和极小值)和处理，形成局部极大值和局部极小值所定义的包络曲面，从而得到局部均值曲面，然后进行相应的筛选过程，最终得到有限个二维固有模态分量(bidimensional intrinsic mode function，BIMF)和趋势项。

1.2 二维经验模态分解筛选过程

按照EMD的思想，给出BEMD的分量曲面筛选过程。对于图像信号F(x,y)，它的上、下包络曲面分别表示为fmax(x,y)和fmin(x,y)，则局部均值曲面m1(x,y)可定义为

(1)

根据BIMF的定义，在理想情况下，第1次筛选结果可以作为第1个分量h1(x,y)，定义为

h1(x,y)=F(x,y)-m1(x,y)

(2)

为了使得均值曲面更加对称，需要继续筛选，第2次筛选以h1(x,y)作为待处理数据。这一过程将被重复多次，直到h1k(x,y)满足BIMF的定义。此时，h1k(x,y)就是从原始信号中获得的第1个BIMF分量，定义为

C1(x,y)=h1k(x,y)

(3)

把C1(x,y)从原信号中分离出的信号R1(x,y)作为新数据进行处理。

R1(x,y)=F(x,y)-C1(x,y)

(4)

依次继续筛选，最终可以得到

(5)

(5)式中：Ci(x,y)为第i个BIMF分量；Rn(x,y)为剩余的趋势项。

筛选过程能平滑不规则的振幅，削弱数据的奇异性，但也会影响图像的物理意义，所以必须确定一个筛选过程停止准则。本文以限制标准差Sd的大小作为判断标准[24]，对2次连续的筛选结果计算Sd，表示为

(6)

(6)式中：hlk(x,y)，hl(k-1)(x,y)分别为2次连续筛选的结果；l表示分量的序号；k表示相应的筛选次数。

同样地，应当设置分解停止准则来决定何时停止分解过程，得到最终的残余趋势项。当分量Cn(x,y)达到比预定值小时停止，或者当剩余分量Rn(x,y)变成单调函数，从中不能再筛选出BIMF时停止。

2 本文方法

本文提出一种基于BEMD的清晰度评价函数，本文方法流程如图1所示，先对图像进行双区域对焦窗口的选择，再将窗口图像进行BEMD分解，提取最高2个BIMF分量并加权，最后计算能量梯度值，求出最终的清晰度函数评价值。

图1 本文方法流程图Fig.1 Flow chart of proposed method

2.1 双区域对焦窗口

BEMD方法中，由于存在筛选算法，如果对整幅图像进行处理，将大大影响到算法的实时性。选择合适的对焦窗口，不但可以减小计算量，提高算法的实时性，还可以进一步提高对焦算法的精确度。

根据视觉习惯固定窗口位置的方法有中央选择法、固定多区域选择法，这2种方法都不适用于目标不在窗口区域的情况。当无法事先预测目标的出现位置时，可以根据图像自身的特征，自适应地选取包含较多边缘细节信息的对焦区域[12]。文献[25]先提出了一种对图像划分子图，再计算每个子图下累积梯度和的单区域对焦窗口选择方法。在实际应用中，若图像具有复杂背景，单区域选择会影响最终的对焦准确性。因此，本文提出了针对复杂背景图像的双区域对焦窗口选择方法，步骤如下。

步骤1利用图像的多尺度特性，选择基于Scharr算子的4个5×5模板[25]，如图2所示。利用这些模板对图像求4方向的梯度并求和作为当前像素点处的梯度信息。

a 0° 方向模板 b 45° 方向模板 c 90°方向模板 d 135°方向模板

图2基于Scharr算子的4方向5×5模板

Fig.2 5×5 external templates with four directions based on Scharr operator

步骤2根据不同大小的窗口在图像中划分区域，并计算每一个区域下的累积梯度值，最终选择具有最大2个值的窗口进行下一步的BEMD分解。区域的划分和累积梯度值的计算式为

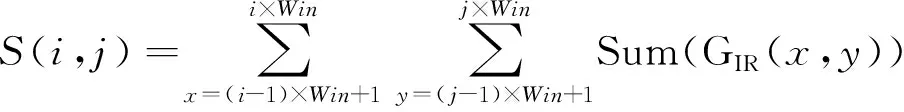
(7)

(7)式中：GIR(x,y)表示所选区域中的梯度图像；Sum()表示在区域内进行梯度累加；Win表示所选择的窗口大小。

对于复杂背景图像，当采用100×100的窗口时，选择结果如图3所示，图3a、图3b分别为原图1、原图2，图3c、图3e为原图1的对焦窗口，图3d、图3f为原图2的对焦窗口。可以看出，双区域选择下的对焦窗口能够更好地体现出原图像的细节信息。

图3 对焦窗口的选择Fig.3 Selection of focusing window

2.2 利用BEMD分解图像

对于对焦图像而言，图像中目标边界处的灰度变化更剧烈，即其边缘处含有更多信息，而这些边缘信息主要包含在图像的最小尺度中[26]。考虑到对焦算法的实时性，可以设定只筛选前2个BIMF分量来进行后续的工作。在图像受到噪声干扰的时候，这2个BIMF分量包含大部分的噪声信息[23]，可以通过给这2个BIMF分量选择不同的加权系数来改善噪声对对焦函数的影响。本文所用的BEMD流程如图4所示。

图4 本文BEMD方法流程图Fig.4 Flow chart of BEMD in proposed method

2.3 能量梯度函数

能量梯度函数是用相邻点的差分计算当前像素下的梯度，可以实现对焦精度在一个像素内，表示为[27]

[I(x,y+1)-I(x,y)]2}

(8)

(8)式中：I(x,y)为图像在点(x,y)处的灰度值；f(I)为评价函数输出结果。

由于能量梯度函数将梯度值平方之后，把边缘的贡献加强了，因此，没有必要再设置阈值[27]。该方法适用于对精度要求比较高的应用场合[28]。

3 精细对焦阶段的评价指标

清晰度评价函数性能好坏大多是通过简单观察评价函数曲线得出的，并不能定量地分析算法性能的优劣，因此，本文提出关于精细对焦阶段的评价指标。在精细对焦阶段，峰值附近函数值变化越剧烈，越容易找到真实的焦平面，当噪声影响较大时，峰值附近函数值变化较为缓和，则对焦过程有可能停止在焦平面附近的虚假焦平面上[29]。文献[29]给出了6个定量指标，其中，对精细对焦阶段清晰度评价函数评估较有意义的是灵敏度指标，定义为

(9)

(9)式中：fmax是对焦曲线的峰值；f(zmax+ε)为横坐标变化时清晰度评价函数的取值。

在噪声影响下，清晰度评价函数可能出现局部峰值和单调性的改变，所以在评价灵敏度的时候，应考虑峰值附近的几个评价值的影响。理想情况下，应该是峰值附近曲线越陡峭越好[2]，因此，本文提出一种新的评价指标——峰值附近的累加差值。曲线越陡峭，峰值和附近几个值的差值应该越大，一旦存在局部峰值或者单调性的改变，差值将会减小，所以可以选取峰值前后的4个值，与峰值计算差值后累加，最终的结果越大，说明清晰度评价函数的灵敏度越高。累加差值的定义式为

(10)

(10)式中：k为清晰度评价函数最大值的序号；f(i)为序号i处的归一化清晰度评价函数值。

4 实验验证

4.1 实验数据

本文实验均在主频为2.5 GHz的Intel(R) Core(TM) i5 CPU、内存为4 GByte、显卡为NVIDIA GeForce 930MX的计算机上实现，所用的操作系统为Windows 7，采用MATLAB2013 (a)平台设计。选取了2组图像作为实验图像，如图5所示，这2组图像均为复杂背景图像，每组图像都体现了离焦—聚焦—离焦的过程。2组图像均由15帧图像构成，大小分别为640×480，720×480，其中每组的第8帧为聚焦图像(第1组图像数据集可以从 https://download.csdn.net/download/qq_42154913/12839310下载得到，第2组图像数据集可以从 https://download.csdn.net/download/qq_42154913/12839312下载得到)。

图5 实验图片Fig.5 Test images

4.2 窗口大小的选择

4.2.1 双区域窗口的选择

在实际应用中，若对复杂背景图像选择单区域窗口，由于参与评价的信息量不够，有可能造成误判。以第1组图像为例说明此问题，如图6所示。当选取单区域窗口时会造成误判，以第7帧图像作为聚焦图像，而选用双区域窗口，则会保证评价函数的无偏性。

4.2.2 窗口大小的选择

对焦窗口的大小也会影响到最终结果，窗口过大会包含太多的背景信息，带来较大的计算量；若对焦窗口过小，虽然计算量小，但容易受到噪声的影响，并且包含的图像信息量过少也不能达到评价效果[12,30]。

分别选取50×50,100×100,150×150,200×200这4种窗口大小。由2组图片得到的归一化评价函数曲线如图7所示。可以看出，4条曲线均满足单峰性、单调性。但对于第1组图像，由于50×50窗口信息量太小，造成了误判。同时，窗口越大计算量越大，如表1所示。不加窗的时候，平均每帧图像的计算时间为12.209 s，随着窗口大小的减小，计算时间依次下降，100×100的窗口计算时间仅为0.943 s，较不加窗的情况下降了92.28%，符合实际应用的需求。综合以上结果，最终选择100×100的对焦窗口。

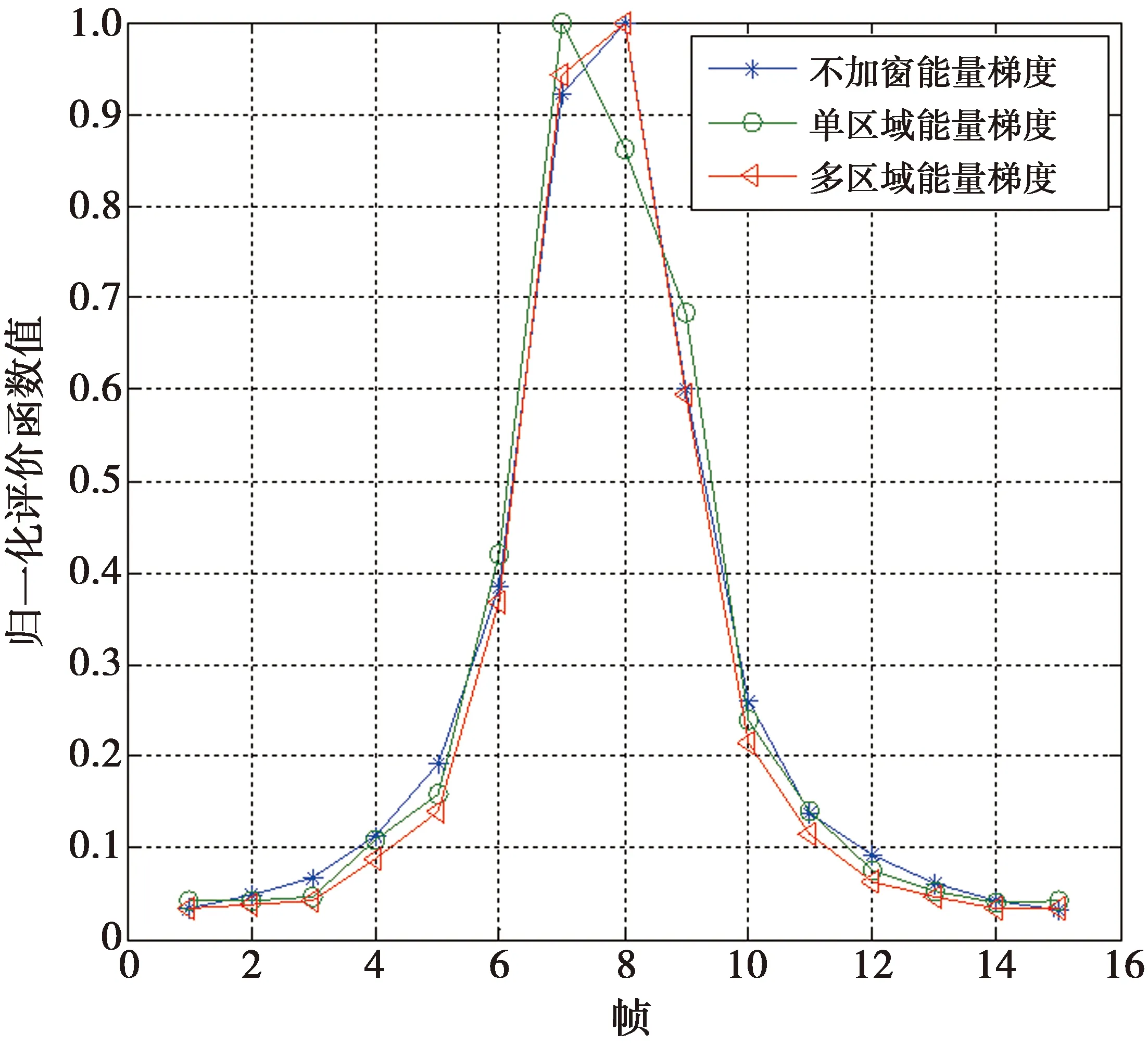
图6 单区域对焦窗口与双区域对焦窗口的比较Fig.6 Comparison of single region and dual-region focusing window

表1 运行时间比较

4.3 BIMF分量的选择

4.3.1 噪声对BIMF分量的影响

经过BEMD，图像的细节信息依次从小尺度到大尺度(即由细到粗)逐一分解出来，而图像的边缘信息主要体现在第1个分量BIMF1中。同时，BIMF1容易受到噪声的干扰，所以给最高的2个BIMF分量添加不同的权重，得到的结果如图8所示。添加的噪声为高斯白噪声(均值为0，方差为0.01)。

从图8可以看出，BIMF1分量比例越小，结果受噪声的影响就越小，当取0×BIMF1+1×BIMF2时，抗噪声能力最强。但由于第1个分量BIMF1的缺失，细节成分丢失太多，评价结果会发生错误，如图8a所示，在第1组图像中，当BIMF1系数取0时出现了局部峰值，而取0.3时也出现了误判。同时，BIMF1分量比例越高，受噪声的影响就越大，当取1×BIMF1+0×BIMF2时，在图像离焦较大的位置，出现了非单调性。当BIMF1的比例大于0.7时，曲线形态就非常接近由原图像直接计算能量梯度的结果，而当BIMF1的比例小于0.3时，就很接近BIMF1系数取0的效果。故将BIMF1系数选择缩小到0.3～0.7。

图7 不同窗口大小的比较Fig.7 Comparison of different focusing window size

4.3.2 BIMF1分量系数的选择

通过分析噪声对BIMF分量的影响之后，进一步探讨BIMF1分量系数的选择。在无噪声影响的情况下，得到的结果如图9所示。可以看出，在没有噪声的影响下，BIMF1系数取0.6或0.5都和原图像的评价结果很接近。为了定量分析，计算BIMF1系数分别取0.6，0.5和0.4时的曲线和原图像对应曲线的欧氏距离，距离越小，说明越接近，如表2所示。综合考虑噪声影响以及评价结果准确性，最终选取0.5×BIMF1+1×BIMF2作为后续计算梯度能量的依据。

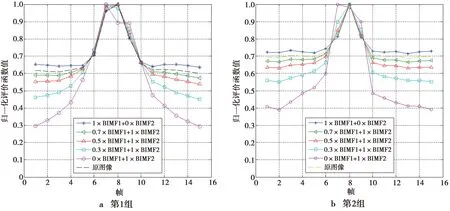
图8 不同加权系数的对比(加噪)Fig.8 Comparison of different weighting coefficient (with noise)

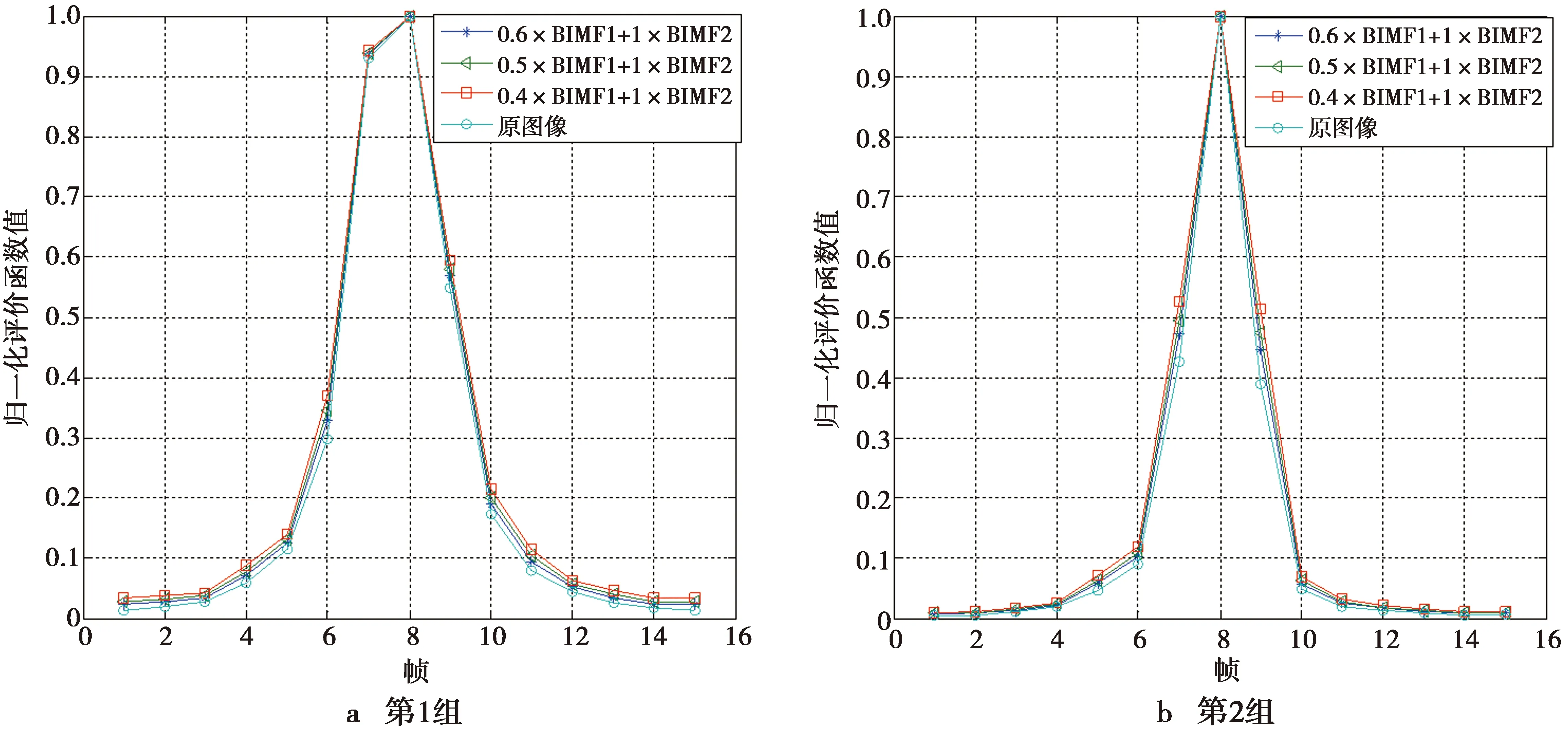
图9 不同加权系数的对比(未加噪)Fig.9 Comparison of different weighting coefficient (without noise)

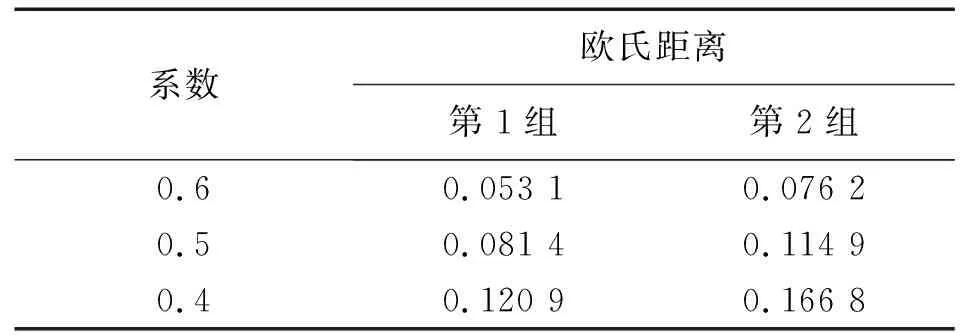
表2 不同BIMF1系数得到的曲线与原图像

4.4 算法性能分析

为了更好地比较本文方法的性能，引入常见的应用于自动对焦的清晰度评价函数，如灰度差分绝对值之和(sum of modulus of gray difference，SMD)[29]、方差[29]、能量梯度[27]、信息熵[27]以及Brenner函数[27]与本文方法进行对比，结果如图10所示。与其他清晰度评价函数相比，在无噪声影响的情况下，方差和信息熵具有单调性，但灵敏度不高，有较宽的覆盖范围，适合作为粗对焦阶段的清晰度评价函数。本文算法以及用Brenner和能量梯度作为评价函数的方法都具备较好的灵敏度，适合作为精细对焦阶段的清晰度评价函数。

对图像加入均值为0、方差分别为0.01和0.02的高斯白噪声后，清晰度评价函数性能比较如图11和图12所示。以SMD，信息熵作为评价函数的曲线灵敏度明显下降；在无噪声情况下，性能较好的能量梯度函数也受到了很大的影响，而本文算法具有较好的抵抗白噪声的能力。

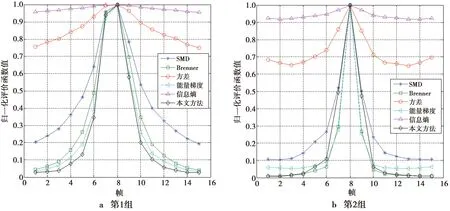
图10 清晰度评价函数性能比较(未加噪)Fig.10 Comparison of definition evaluation functions (without noise)

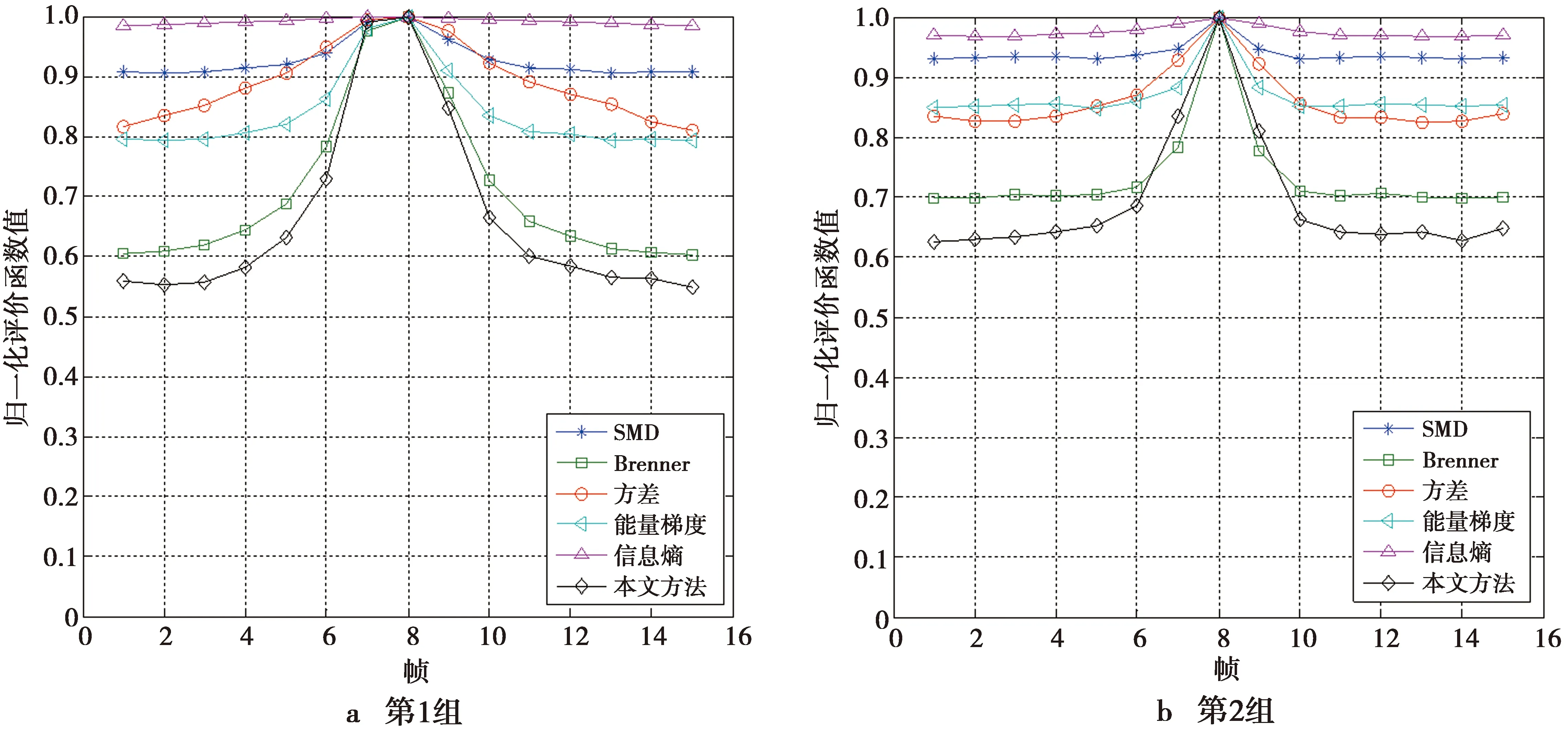
图11 清晰度评价函数性能比较(方差为0.01的高斯噪声)Fig.11 Comparison of definition evaluation functions (Guassian noise with variance of 0.01)

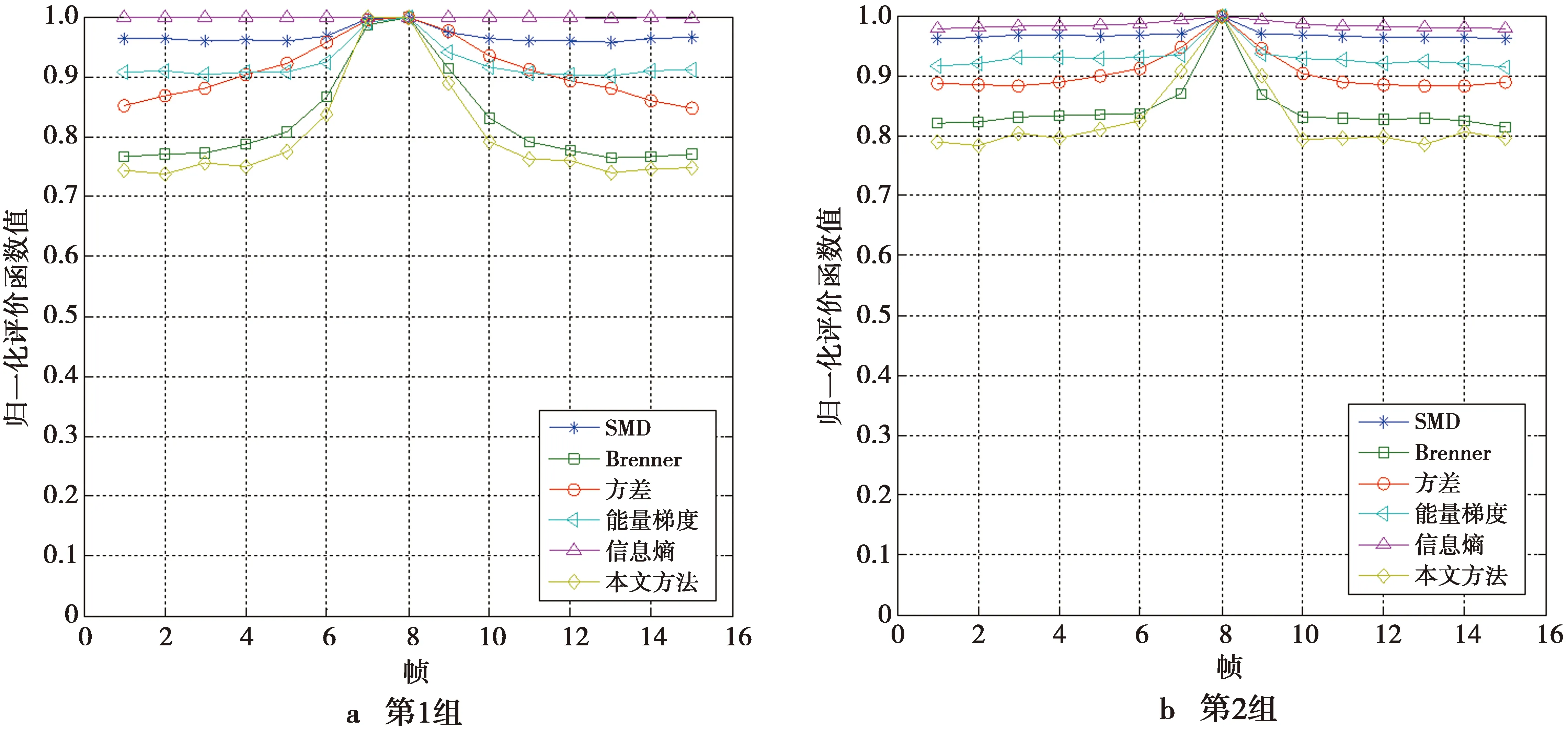
图12 清晰度评价函数性能比较(方差为0.02的高斯噪声)Fig.12 Comparison of definition evaluation functions (Guassian noise with variance of 0.02)

对图像加入方差为0.01的乘性噪声后，清晰度评价函数性能比较如图13所示。对于第1组图像，本文算法依旧具有较好的抵抗白噪声的能力；对于第2组图像，除了信息熵方法以外，其余算法都出现了非单调性，但对本文算法的影响是最小的。

图13 清晰度评价函数性能比较(乘性噪声)Fig.13 Comparison of definition evaluation functions(with speckle noise)

对2组图像分别计算不含噪声和不同噪声情况下的累加差值并取平均值，结果如表3所示。由于方差和信息熵的方法不适用于精细对焦阶段，SMD抗噪性能较差，所以实验中只比较了能量梯度、Brenner和本文算法。从表3中可以看出，在第2组图像加入方差为0.01的高斯白噪声以及乘性噪声情况下，本文方法略微低于Brenner算子，其余含噪声情况下，本文方法得到的累加差值都是最大的，即灵敏度最高。在不含噪声情况下，本文方法在第1组图像中的累加差值是最大的，但在第2组图像中的灵敏度却低于能量梯度和Brenner这2种方法，这是源于将涵盖细节信息的BIMF1分量牺牲了一部分(对BIMFI分量的加权系数只取0.5)来换取抗噪性能，造成了灵敏度的轻微下降。

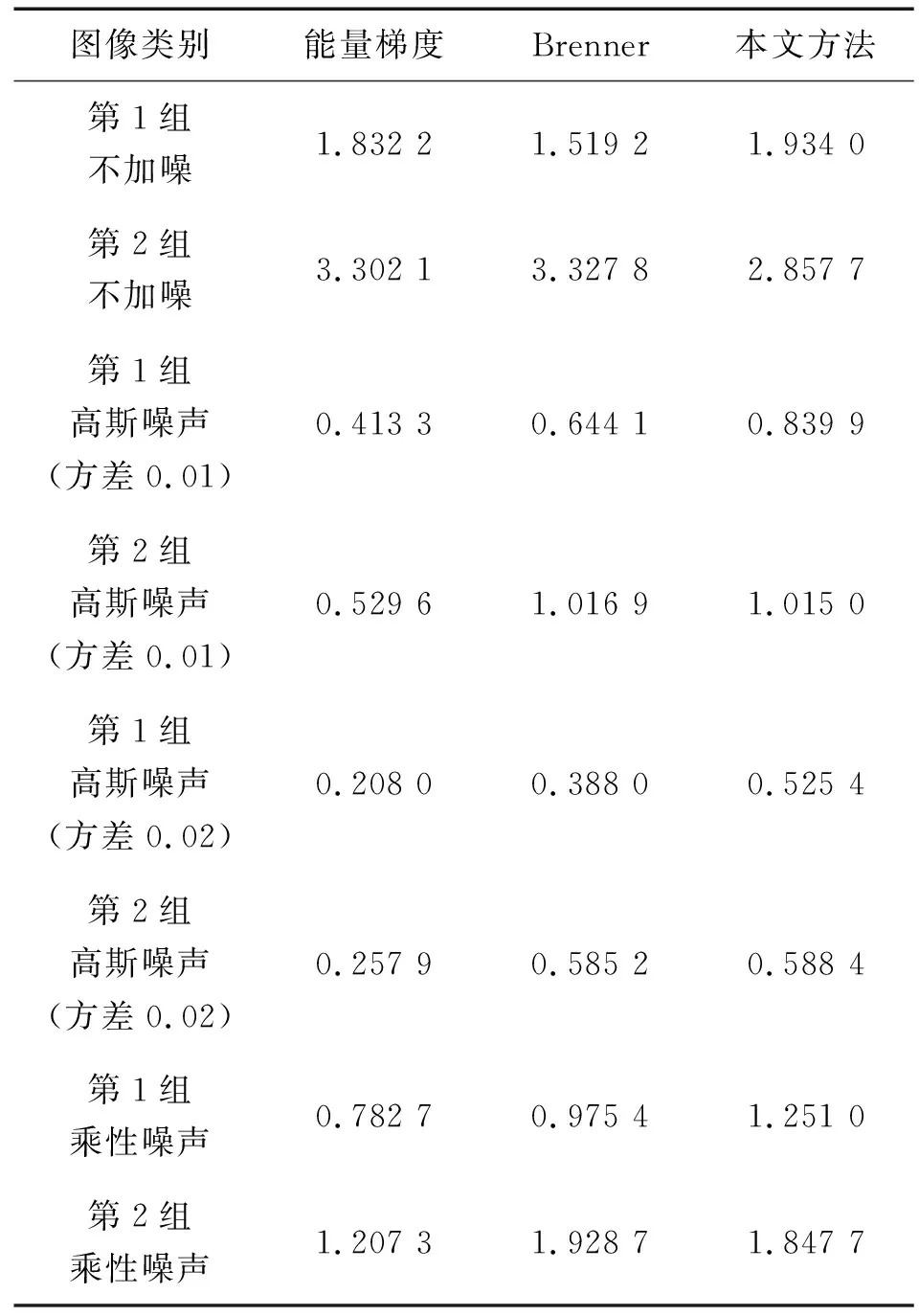
表3 累加差值比较

5 结束语

为了充分利用图像的多尺度特性，并改善常用图像清晰度评价函数对噪声敏感的问题，本文提出了一种基于4方向Scharr算子及BEMD的清晰度评价函数。BEMD可以将图像从小尺度到大尺度层层分解，但筛选过程中计算量较大，算法实时性不强。本文方法利用4方向Scharr算子进行双区域窗口选择，以减少计算量并提高对焦准确性。实验结果表明，双区域窗口可以避免误判，同时也可将每帧图像的计算时间降低。利用BEMD分解出的BIMF1和BIMF2分量包含较多图像细节的特点，将这2个分量加权可以提升评价函数的抗噪性能。为了对结果进行定量分析，本文提出了精细对焦阶段灵敏度评价指标——累加差值。实验结果表明，本文方法在有噪声情况下仍然具备较好的灵敏度，抗噪能力较强。