基于模糊神经网络的啤酒灌装精度控制技术

刘 伟

(吉林电子信息职业技术学院电气工程学院，吉林 吉林 132000)

随着自动化技术的发展以及市场竞争的加剧，全自动灌装机成为灌装生产线上不可或缺的设备，在食品、医药等行业中扮演着十分重要的角色[1-2]。灌装的效率和精度是衡量企业生产能力的重点指标，但就实际生产而言，部分企业还依靠人工手动调整灌装精度，生产效率低，生产成本高。虽然也有企业采用了自动化生产设备，但精度低、稳定性差。

灌装是啤酒生产过程中的关键环节。灌装机系统复杂，控制要素多，既要实现对流量、压力以及重量等指标的过程控制，还要同步控制传动系统的运动速度和位置[3]。传统灌装过程需要人工复检，效率低，成本高，且采用的常规PID控制方法参数不能实时调节，有一定的局限性。因此，学者们[4-7]不断将模糊算法、神经网络算法等先进控制理念融入到灌装过程中。其中，模糊控制具有抗干扰能力强的特点，能有效解决多变量、非线性等问题，但模糊规则的制定受主观因素影响大，缺乏自学习能力；神经网络控制是模拟人脑结构机理来实现对复杂系统的控制，具有很强的自学习能力，但不适用于表达基于规则的知识，容易陷入局部最优问题。

针对饮料产品自身特点及食品生产要求，研究拟将模糊算法与神经网络算法相结合，提出一种模糊神经网络PID(FNN-PID)控制策略，使系统既具备推理归纳能力，又具有自适应能力，从而实现PID参数的动态调整，旨在为提高啤酒灌装机的精确性和稳定性提供依据。

1 灌装机结构及工作流程

灌装机工作流程包括清洗、传送、灌装、封装等，其中灌装是灌装机的核心工序[8]。灌装机构主要由传送带伺服机构M1、灌装伺服机构M2、称重装置、液体充灌装置以及重量检测装置等组成(图1)。

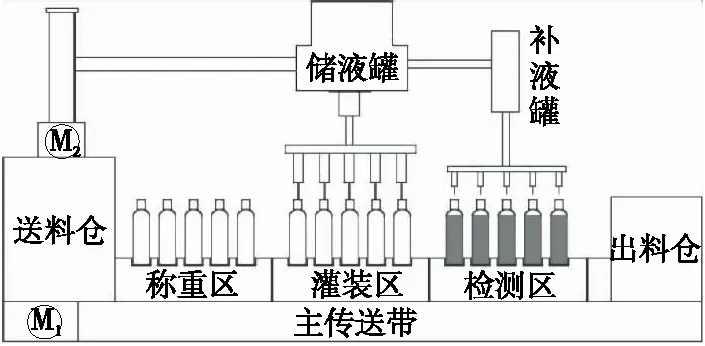
图1 灌装机结构Figure 1 Structure of filling machine

该灌装机采用重力式灌装方式，分为称重区、灌装区以及检测补灌区3个工位。为提高灌装速度，共设5个主灌装接头和5个补灌接头，可根据生产需求在触摸屏上设置传送带速度、灌装重量以及灌装时间等参数。当按下启动按钮后，传送带将称重后的空瓶送至灌装区，灌装接头下降至灌装位置，开启阀门，完成初次灌装任务。受泡沫、喷溅等因素影响，灌装的容积或重量存在一定误差，因此灌装完成后，需对灌装结果进行精度检测，不满足条件的需进行二次灌装。试验目的是验证控制策略在灌装机上的应用效果，因此只对二次补灌过程进行控制，以重量偏差为研究指标，具体灌装步骤为：

(1) 称重区进行空瓶称重，并确认是否有灌装瓶。

(2) PLC控制伺服电机M1带动传送带将待灌装的空瓶传送至灌装区。

(3) 伺服电机M2驱动灌装接头下降至灌装位置。

(4) 按照设定参数开始第一次灌装。

(5) 初次灌装完成后，传送带将灌装好的饮料瓶送至检测区，并将未灌装的空瓶同步送至灌装区，做好下一次灌装准备。

(6) 对已灌装的饮料瓶进行重量检测，计算瓶内液体的重量。

(7) 计算重量偏差，采用FNN-PID控制器进行二次补灌。

(8) 当检测值与设定值相同时，灌装完成。

2 控制系统设计

2.1 控制系统组成

控制系统由上位机、PLC控制器、传感器、伺服电机、驱动器以及电磁元件等模块组成(见图2)。PLC控制器是系统的核心，在收到传感器采集的流量、位置、重量等数据信息后，根据设计要求向执行元件发送控制指令，控制伺服电机、电磁开关等执行器工作[9-11]。上位机主要用来监测灌装过程，实现人机交互，具有参数设定、故障报警、数据监控等功能。

图2 灌装控制系统组成Figure 2 Composition of filling control system

2.2 模糊神经PID控制器结构

为保证灌装精度，需解决系统存在的时变性问题。模糊神经网络结合了模糊控制精度高和神经网络自学习能力强的特点，在控制参数发生变化时只需更新样本数据重新训练即可，可移植性较强[12-13]。因此，采用模糊神经网络在线更新PID参数，模糊神经网络PID控制器结构如图3所示。

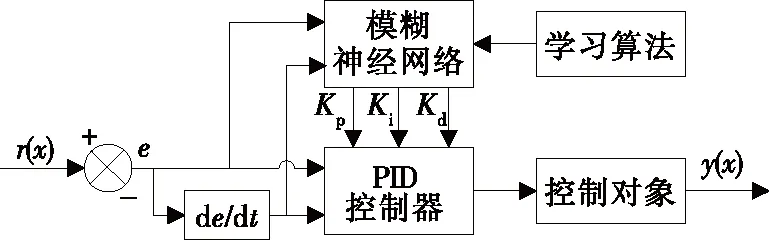
图3 模糊神经网络PID控制器结构Figure 3 Fuzzy neural network PID controller structure

试验设计的模糊神经网络采用双输入结构，输入神经元是灌装重量的偏差和偏差变化率，输出神经元为PID的3个性能指标参数Kp、Ki、Kd，包括输入层、模糊化层、模糊推理层以及输出层4个层级结构(见图4)。

图4 模糊神经网络结构Figure 4 Fuzzy neural network structure

(1) 输入层：两个输入变量分别代表灌装重量的偏差e和偏差变化率ec，分别对应两个神经元节点，并通过激活函数输出到模糊化层，其表达式为

f1(x1)=xi。

(1)

(2) 模糊化层：将输入变量e和ec模糊化，利用高斯函数[式(2)]作为评价标准，计算各语言变量作为隶属度函数的输入变量，从而达到模糊化的目的。

(2)

式中：

cij、σij——高斯函数的中心位置和宽度。

(3) 模糊推理层：该层中节点和模糊规则是一一对应的，作用是进行模糊推理，用于计算每条规则对于各自节点的适应度，所采用的激活函数为

(3)

式中：

N——神经元之和。

(4) 输出层：实现变量的反模糊化，连接PID控制器的3个参数Kp，Ki，Kd。所采用的激活函数为

(4)

即

(5)

式中：

ω——模糊推理层与输出层之间的连接权重。

根据系统控制特点，采用Delta(x)函数确立学习规则，使用梯度下降法实现网络训练的调控，进行隶属度参数及输出权值的学习训练，实现系统自适应和快速逼近实际值的目的，其目标函数为：

(6)

式中：

r(k)——理想输出；

y(k)——实际输出。

2.3 模糊推理规则

将训练样本输入到模糊神经网络的输入层中进行离线训练，直到满足设定要求。利用映射关系将模糊逻辑和神经网络相结合，将模糊规则、隶属度函数转化为模糊神经网络的权重，利用神经网络的自学习能力来修正权重，不断逼近设定值，达到模糊推理的目的。

对模糊子集的语言变量进行设置：定义模糊子集为{NB，NM，NS，ZO，PS，PM，PB}，即{负大，负中，负小，零，正小，正中，正大}，e、ec的论域均为[-1，1]。控制规则是模糊控制器的核心，取决于专家的经验和推理。针对灌装的工作特点制定ΔKp、ΔKd、ΔKi的模糊控制规则如表1～表3所示。

表1 ΔKp控制规则表Table 1 Control rule table of ΔKp

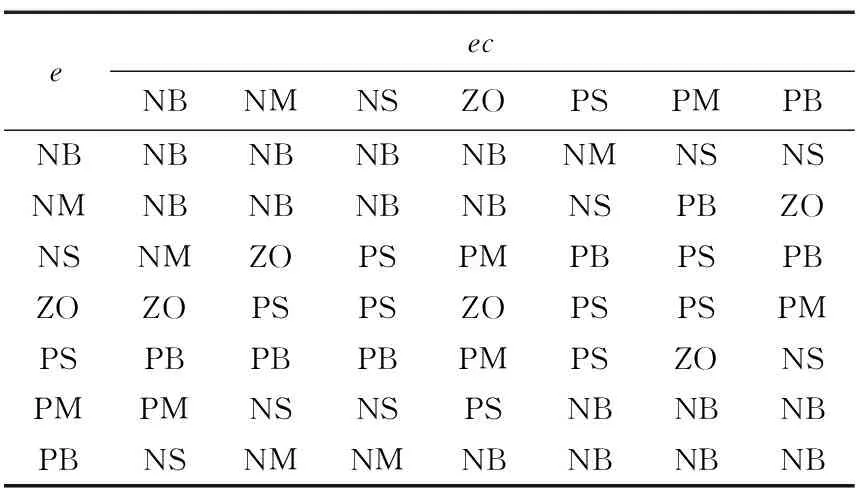
表2 ΔKi控制规则表Table 2 Control rule table of ΔKi

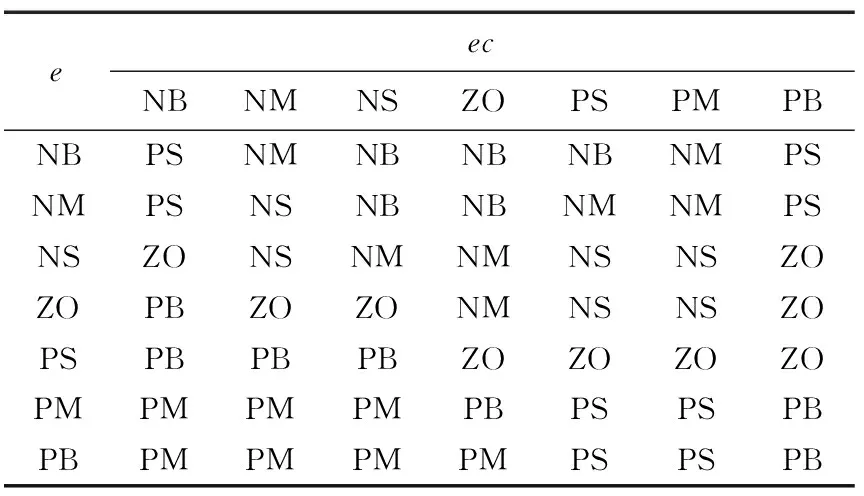
表3 ΔKd控制规则表Table 3 Control rule table of ΔKd

2.4 灌装控制流程

将FNN-PID控制算法应用于二次灌装控制过程中，进一步提高灌装精度。在完成初次灌装后进入检测区进行称重，根据两次称重结果计算灌装液体的重量，利用测量值与目标值之间的重量偏差进行补灌控制，FNN-PID控制流程如图5所示。

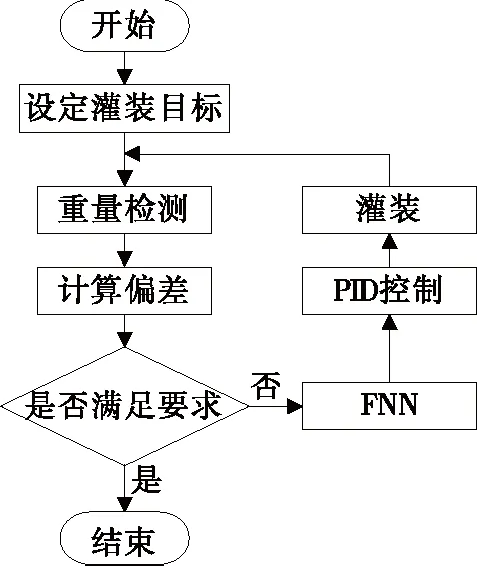
图5 FNN-PID控制流程Figure 5 FNN-PID control flow

3 仿真与结果分析

为验证所设计控制方法的有效性，在MATLAB软件中使用Simulink建立仿真模块，将FNN-PID控制算法调入模型中进行阶跃响应仿真分析，并与常规PID及模糊PID进行对比，结果如图6所示。

为进一步说明几种算法的控制效果，将图6中曲线进行量化处理，从峰值时间、峰值、超调量、调节时间4个指标进行对比分析，结果见表4。

图6 阶跃响应对比情况Figure 6 Step response comparison

由表4可知，与其他算法相比，FNN-PID算法超调量最小，达到稳定状态时仅需2.81 s。与常规PID控制相比，FNN-PID的超调量和调整时间分别提高了67%和55%，具有控制精度高、响应速度快、鲁棒性好等特点，符合灌装生产高效、准确的控制要求。

表4 仿真对比结果Table 4 Simulation comparison results

4 实验验证

搭建灌装试验平台，因灌装装置只在补灌工序中实施了模糊神经控制，所以测试中忽略初次灌装工序，只对补灌流程进行性能测试。试验中先以100 g为目标重量进行灌装，共进行3组测试，每组测试分别采用常规PID、模糊PID以及FNN-PID进行控制灌装。每个补灌接口各灌装12瓶，5个接口共灌装60次，即3种控制方法各灌装20次。要求灌装精度为±3 g，产品合格率要求≥98.5%，灌装完成后，在同一测量装置上进行称量并记录结果，忽略测量误差，结果见表5。采用同一方法以200 g为目标重量进行第二次测试，要求灌装精度为±5 g，产品合格率要求≥98.5%，结果见表6。

由表5可知，当灌装目标为100 g时，PID控制平均灌装误差为2.0 g，最大绝对误差为4.2 g；模糊PID控制平均灌装误差为1.5 g，最大绝对误差为3.5 g；FNN-PID控制平均灌装误差为0.5 g，最大绝对误差为0.9 g。由表6 可知，当灌装目标为200 g时，PID控制平均灌装误差为3.5 g，最大绝对误差为5.7 g；模糊PID控制平均灌装误差为3.2 g，最大绝对误差为5.1 g；FNN-PID控制平均灌装误差为1.7 g，最大绝对误差为3.2 g。从合格率角度看，3种控制方案的合格率分别为90%，95%，100%。为使分析更为直观，将以上结果进行绘图对比(见图7、图8)。

表5 灌装目标为100 g时的结果Table 5 Results of the filling target with 100 g

表6 灌装目标为200 g时的结果Table 6 Results of the filling target with 200 g

由图7、图8可知，FNN-PID控制精度高、稳定性好，与常规PID及模糊PID控制相比，平均精度分别提高了49.5%，44.5%。

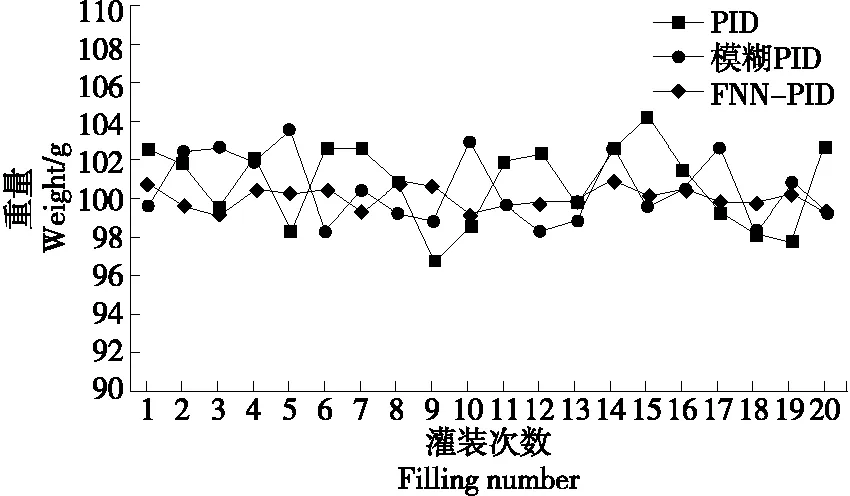
图7 灌装目标为100 g时对比曲线Figure 7 Comparison curve of the fillin target with 100 g

图8 灌装目标为200 g时对比曲线Figure 8 Comparison curve of the filling target with 200 g

5 结论

以PLC控制为基础，结合模糊算法抗干扰能力强以及神经网络算法自学习能力好的优势，提出了一种基于模糊神经网络的灌装机PID控制算法，并将其应用于饮料灌装过程中。结果表明，基于模糊神经网络的灌装机PID控制算法响应速度快，相比常规PID控制提高了55%，可大大提高灌装机的工作效率。基于模糊神经网络的灌装机PID控制算法具有较高的控制精度，最大偏差仅1.7 g，灌装合格率为100%，灌装精度相比常规PID控制的提高了50%，满足自动生产线运行稳定、快速、可靠的要求。后续可对整个灌装流程进行优化。