智能反射面辅助雷达通信双功能系统的多载波波形优化方法

田团伟 邓浩* 鲁建华 杜晓林

①(河南大学物理与电子学院 开封 475001)

②(空军航空大学航空作战勤务学院 长春 130022)

③(烟台大学计算机与控制工程学院 烟台 264005)

1 引言

作为现代电磁理论的两个主要应用[1]，雷达与通信长期独立发展并逐渐升级为多功能设备，两者的宽带化、网络化趋势导致了频谱资源拥挤，降低了雷达与通信效能。对此，基于雷达与通信系统之间的相似性，众多学者与机构开展了波形处理与资源管控有机一体方案的研究。雷达通信一体化可有效降低复杂电子信息系统冗余、能耗等，是未来信息技术的发展趋势[2–6]。

同时实现雷达通信双功能(Dual-function Radar-Communication,DRC)是雷达通信一体化的重要研究方向，其主要目标为利用一套设备同时实现雷达与通信功能。DRC可应用于包括车联网、室内定位以及隐蔽通信在内的诸多民用及军用场景[7]。

在不同时隙、频带或者码字完成雷达与通信功能是易于实现的DRC系统[8,9]。时分复用一体化最早应用于美国国家航空航天局轨道飞行器系统[10]，并广泛应用在智能交通系统[11–13]；频分复用一体化在不同频段内传输雷达与通信信号[14–17]；而码分复用一体化采用不同伪随机(正交)码分别调制雷达与通信信号并进行合成[18–20]。然而，文献[10–20]所研究的波形设计方案无法充分利用时间、空间、频谱和码字等资源。对此，众多学者开展了利用同一波形同时实现雷达与通信功能的研究，目前可分为通信共用波形和雷达共用波形两类。

通信共用波形设计是指采用现有或经过改动的通信波形同时实现雷达与通信功能[21–24]。文献[25]和文献[26]分别研究了宽带信号和存在多个目标的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)波形设计问题。Sit等人[27]于2011年采用OFDM通信信号测量多个目标的速度参数。李自琦等人[28]于2014年提出了分组并行格雷编码结合加权系数优化的OFDM峰均功率比抑制算法。通信共用波形需要设计新的雷达处理方式，进而造成雷达性能下降；若通过调整通信波形以提升雷达性能，通信性能会相应下降。因此，通信共用波形需要在雷达与通信性能之间进行折衷考虑。

雷达共用波形设计是指将通信符号嵌入到现有雷达脉冲(串)，以实现雷达与通信功能。目前，该双功能实现方案主要有快时间信息嵌入和方向图调制信息嵌入。快时间信息嵌入是指通过调制多个脉冲的波形信息以传输通信符号。2016年，Nowak等人[29]通过控制脉冲间波形的相位信息将通信符号嵌入到雷达波形。Gaglione等人[30]于2018年利用调频斜率不同的线性调频信号的准正交性实现了通信符号嵌入。Liu等人[31]于2018年通过设计类似通信符号的雷达发射波形以同时实现雷达与通信功能。Edara等人[32]于2018年提出了采用跳频和相移键控采样策略的快时间信息嵌入方案。然而，快时间信息嵌入技术功率和频谱效率低，进而导致雷达性能下降。

方向图调制信息嵌入是指通过控制发射波束的旁瓣信息将通信符号嵌入到雷达波形中以同时实现雷达与通信功能。2015年，Hassanien等人[33,34]提出了基于幅度调制的信息嵌入方案(Amplitude Shift Keying-Information Embedding,ASK-IE)。该方案通过控制指向通信用户方向的旁瓣幅度，将通信符号嵌入到雷达发射波形中。每个旁瓣幅度对应一个通信符号，通信接收端通过解调接收信号的幅度，进而判断对应的通信符号。同年，Hassanien等人[35]又提出了基于相位调制的信息嵌入方案。2018年，Ahmed等人[36]提出了基于正交振幅调制的信息嵌入方案(Quadrature Amplitude Modulation-Information Embedding,QAM-IE)，通过同时控制通信用户方向的旁瓣幅度与相位同时实现雷达与通信功能。基于方向图调制信息嵌入方案，Tian等人[37]于2020年研究了OFDM-DRC的功率优化问题；于2021年研究了DRC发射/接收波束联合优化问题，提出了交替方向松弛规划(Alternating Direction Sequential Relaxation Programming,ADSRP)算法，在双功能同时实现前提下优化了DRC的探测性能[38]。

在候选通信性能增强方案中，智能反射面(Intelligent Reconfigurable Surface,IRS)以其独特的低成本、可编程、易部署的特点受到了众多学者的关注[39–41]。Huang等人[42]于2020年设计了IRS被动波束向量以最大化最小信干噪比(Signal-to-Interference-Noise Ratio,SINR)。De Jesus Torres等人[43]于2021年研究了不同IRS阵元数下电磁干扰对IRS辅助通信系统性能的影响，指出当通信发射机与接收机之间的链路性能较差时，IRS的存在可能会降低通信性能。Wang等人[44]于2020年研究了IRS辅助多输入单输出系统的稳健波束与相移设计问题。崔铁军院士团队[45–48]完成了基于IRS的单/多输入、单/多输出实时传输以及IRS自由空间路径损耗的测量。

IRS也在雷达检测、监视、涡旋波束设计等领域得到了应用[49–52]。Buzzi等人[53]于2021年研究了IRS辅助雷达系统的检测问题，指出IRS与雷达发射/接收机的距离会影响系统性能：距离较近时(即近距离IRS)能获得显著的性能提升；然而，远距离IRS仅能获得有限的性能提升。Wang等人[54]于2020年研究了IRS辅助的多输入多输出雷达与多用户多输入单输出通信系统之间频谱共享问题；于2021年研究了IRS辅助DRC (I-DRC)系统的波形与被动波束设计问题，提出了基于流形优化的交替算法以最小化多用户之间的互干扰[55]。对此，在文献[33–38]介绍的方向图调制信息嵌入技术基础上，本文面向近距离IRS辅助的雷达探测为主、数据传输为辅的场景，设计I-DRC系统的多载波波形，在双功能实现前提下有效提升DRC探测及数据传输性能。主要贡献如下：

(1) 由于发射/接收天线的阵列结构扩展了自由度，本文联合优化双功能发射波形、IRS反射单元以及雷达和通信接收机，并采用传输功率、通信码字错误率(Word Error Probability,WEP)、旁瓣幅度与IRS反射系数约束下雷达互信息(Radar Mutual Information,RMI)最大化为优化准则。

(2) 由于待优化问题为非凸的，本文提出了基于交替方向最大化(Alternating Direction Maximization,ADM)的多载波波形优化算法，将原高维非凸优化问题分解为低复杂度的双功能发射波束、IRS反射系数以及雷达与通信接收波束设计子问题并迭代优化，获得了多载波波形功率分配策略的局部最优解。

(3) 给出了一系列I-DRC仿真性能曲线，分析了近距离IRS对雷达探测性能的影响，验证了ADM算法可同时实现雷达与通信功能；相较于现有算法，有效提升了雷达探测性能及WEP性能。

符号说明：和分别表示转置、共轭转置、共轭、范数、取绝对值、取均值和取实部操作；vec{·}表示将矩阵按列排列形成列向量；trace(·)和 diag{·}分别表示矩阵的迹和对角元素；⊗表示Kronerker积；C为复数集合；CN×1为包含N ×1向量的复数集合；CN×N为包含N ×N矩阵的复数集合；IN×N表示N ×N维单位矩阵；CN(·,·)表示高斯分布。

2 系统模型

考虑一个包含双功能发射共置阵列、IRS、雷达和通信接收共置阵列的I-DRC系统，如图1所示。其中，双功能发射共置阵列包含NT个阵元，IRS包含M个阵元，雷达与通信接收共置阵列分别包含NR,r和NR,c个阵元。不失一般性，假设所有阵列均为阵元间隔为半波长的均匀线性阵列；雷达与通信接收阵列的阵元数相同，即NR,r=NR,c=NR；双功能发射阵列和雷达接收阵列以同一方位角观察远距离目标，且模型中涉及的方位角已知；IRS与双功能发射机的距离较近，即近距离IRS[53]；最后，假设雷达与通信信道状态信息(Channel State Information,CSI)已知[38]。

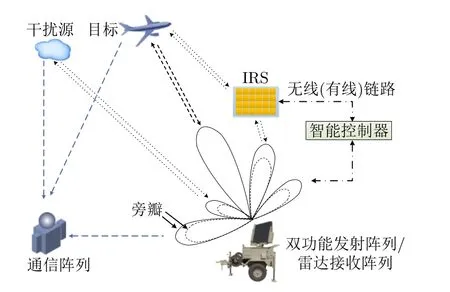
图1 I-DRC基本框架Fig.1 Basic frame of I-DRC

2.1 雷达功能

令双功能发射共置阵列与目标、干扰源以及IRS之间的信道分别为和TIRS和目标之间的信道为IRS的反射系数为q=(q1,q2,...,qM)T，其中，qm=为反射幅度，υm=[0,2π]为反射相位。假定探测目标、干扰源以及IRS分别位于方位角θ0,θ1以及θris，IRS与探测目标之间的方位角为θrist，则雷达接收阵列处第k个子载波上等效基带接收信号为

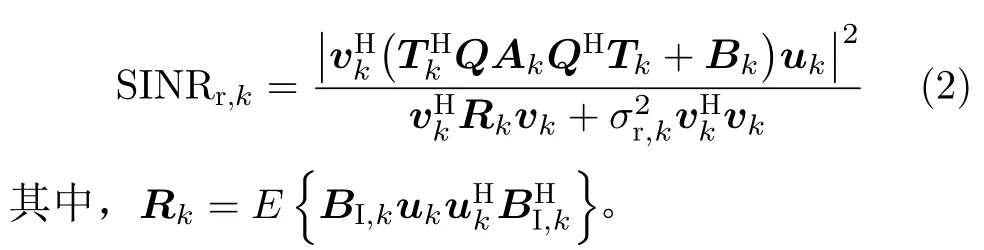
在Mark于1993年将RMI作为雷达系统的评价指标后[56]，RMI被广泛应用于成像[57]、跟踪[58]及雷达波形设计[59–62]。RMI用来衡量观测到的目标信息量，RMI值越大，表明回波信号yr,k中包含的目标信息量越多，进而获得更好的探测性能。由文献[63,64]可知，RMI为雷达SINR的函数，可表示为

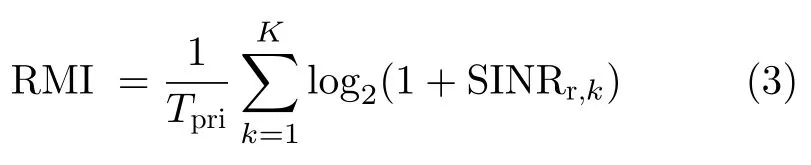
其中，Tpri为脉冲重复间隔。由式(3)可知，SINRr,k越大，RMI越大。

2.2 通信功能

假定通信接收阵列位于方位角φ，则第k个子载波上等效基带通信发射信号为

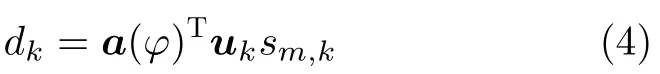
通信符号的传输通过控制式(4)的幅值(指向方位角φ的发射波束旁瓣电平)实现。dk对应一个唯一的通信符号，为在每个子载波上传输log2(L)比特符号(一个脉冲持续时间)，需要设计L个dk不同的发射波束并存储在码字字典D={d1,k,d2,k,...,dL,k}。因此，在脉冲持续期间，从D中选择一个dℓ,k(ℓ=1,2,...,L)；在通信接收端，通过判断dℓ,k(ℓ=1,2,...,L)以确定所对应符号，进而完成符号传输。

通信接收阵列处的信号包含来自双功能发射阵列的有用信号以及探测目标/干扰源反射的干扰信号，则第k个子载波上等效基带接收信号可表示为

定义wk ∈为第k个子载波上NR×1的通信接收波束形成矢量，则在通信接收阵列处，接收信号yc,k经由wk滤波后，得到第k个子载波上通信SINR，即

其中，ds,k为不同于dℓ,k的码字。

3 I-DRC多载波波形优化算法设计

针对I-DRC的多载波波形优化问题，其优化过程需达到以下3个目标：(1)最大化RMI；(2)完成符号传输；(3)满足WEP要求。因此，采用传输功率、WEP、旁瓣幅度与IRS反射系数约束下RMI最大化为优化准则，待解决问题为

其中，约束C1表明发射功率不能超过Pt,θall为所有方位角的集合；约束C2意味着WEP不能超过期望值；约束C3控制指向方位角φ的旁瓣幅度，以完成通信符号传输；约束C4表明IRS是被动的，不放大来波信号，仅进行相位调整，其相位信息经由智能控制器控制。此外，由约束C3可知，为传输log2L比特符号/脉冲，优化问题(8)需求解L次。

由于目标函数关于uk,Q,vk和wk的非凹性，优化问题(8)为高维非凸优化问题。受到文献[65,66]所提算法的启发，并利用目标函数的可分性结构，即

其中，ε为预先设置的迭代停止常数。

3.1 uk设计子问题

其中，常数1/Tpri已省略。由于目标函数关于uk是非凹的，优化问题(12)是非凸的，接下来求解其等价松弛凸问题。

引入满足如下条件的松弛变量ϖk

则优化问题(12)等价于如下优化问题

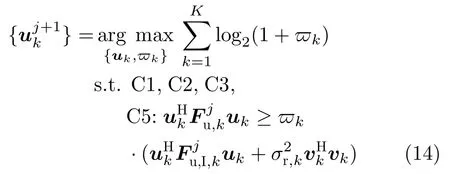
由于约束C5关于uk的非凸性，优化问题(14)为非凸的。根据一阶泰勒展开条件[67]可知，满足如下条件：

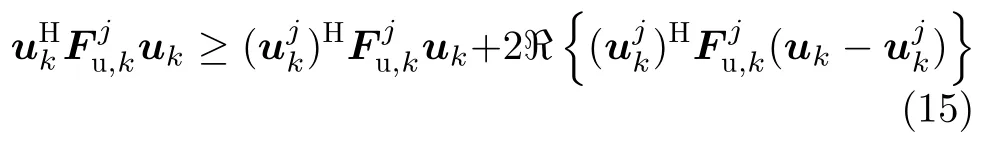
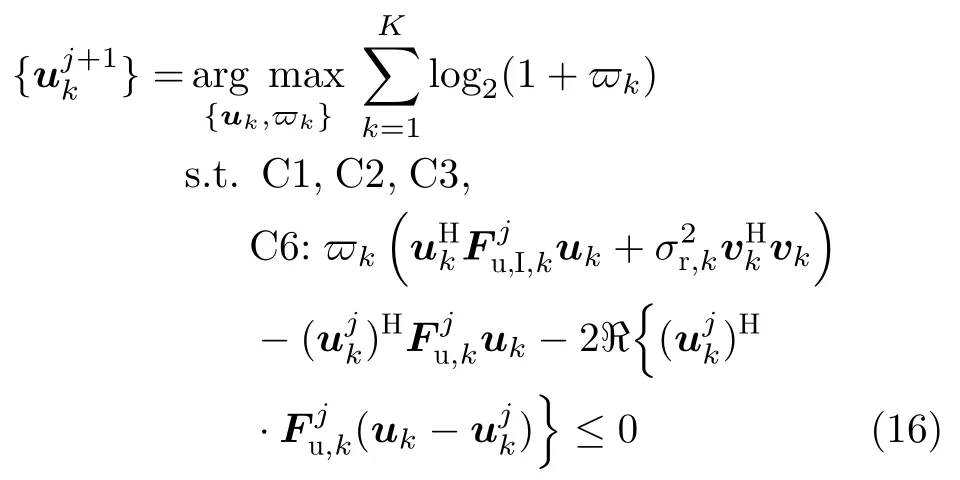
松弛优化问题(16)为凸的，其最优解可通过CVX工具箱[68]获得。

3.2 Q设计子问题

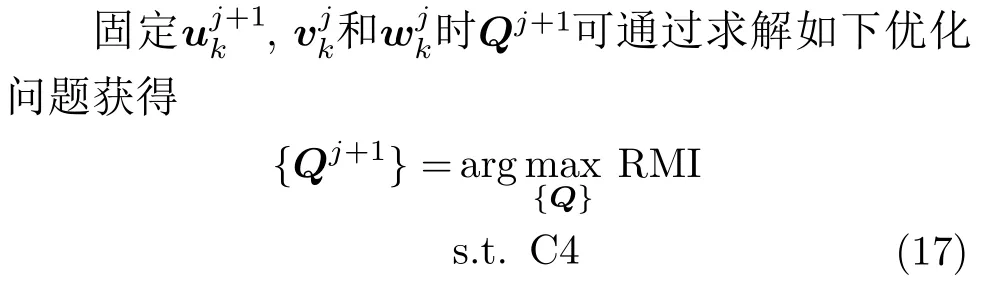
由于RMI是雷达SINR的单调递增函数且K个子载波相互独立，上述优化问题等价于如下优化问题：

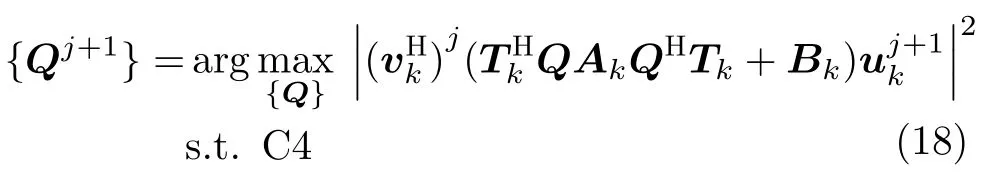
考虑到恒模约束的存在，上述优化问题的求解则较为复杂，接下来求解其等价松弛凸问题。

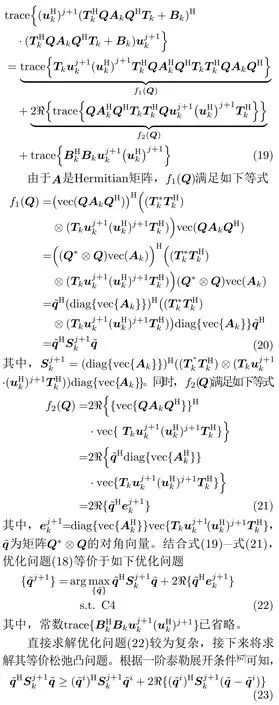
3.3 vk设计子问题

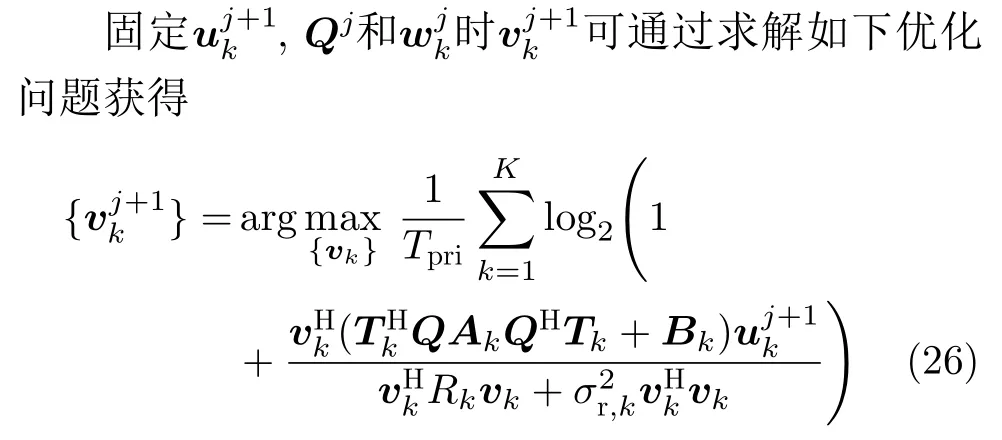
由于RMI是雷达SINR的单调递增函数且K个子载波相互独立，优化问题(26)等价于如下优化问题：

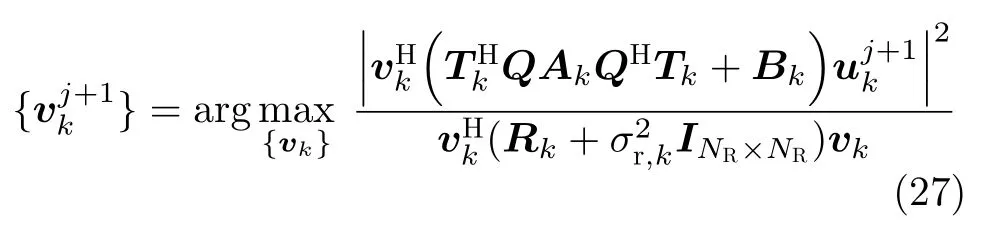
优化问题(27)可等价为最小方差无畸变响应(Minimum Variance Distortionless Response,MVDR)波束形成问题[69]，即

3.4 wk设计子问题

优化问题(30)可等价为MVDR波束形成问题，即

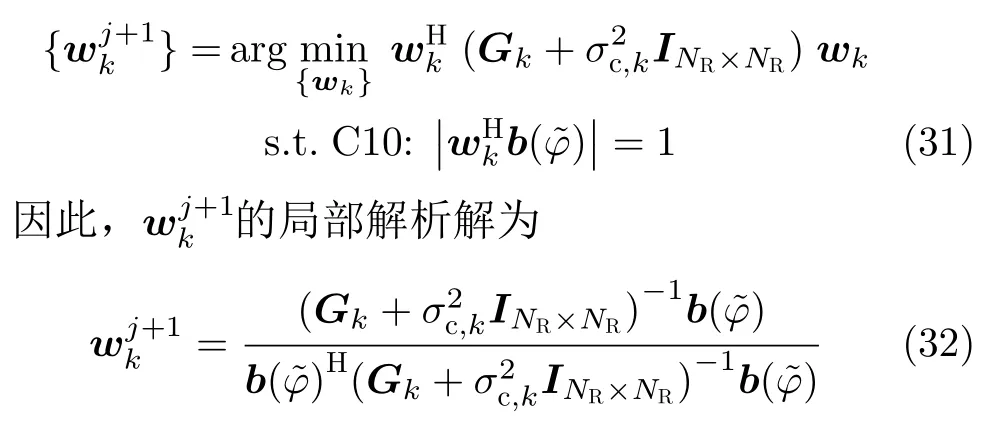
ADM算法迭代过程总结于表1。

表1 基于ADM的多载波波形优化算法Tab.1 ADM based multicarrier waveform optimization method

3.5 算法复杂度与收敛性分析

3.5.1 复杂度分析

3.5.2 收敛性分析

此外，由于SINRr,k的有界性[70,71]且RMI(uk,Q,vk,wk)为SINRr,k的单调递增函数，蒙特收敛理论[72]保证了ADM算法的收敛性。

4 仿真结果与分析

本节通过仿真实验验证ADM算法性能并评估IRS对I-DRC系统性能的影响，仿真场景如图2所示。假设探测目标、IRS与干扰源分别位于方位角θ0=0◦,θris=15◦与θ1=60◦，IRS与探测目标之间的夹角为θrist=30◦；子载波数为K=16；发射/接收阵元数均为NT=NR=16，IRS阵元数为M=16；通信接收阵列位于方位角φ=40◦，并预先设计L=2种旁瓣幅度，即d1=−10 dB和d2=−20 dB。以通信接收阵列的角度，从方位角=0◦接收有用信号，并受到来自方位角ϕ0=50◦和ϕ1=70◦的信号的干扰。如无特别说明，假定雷达与通信的噪声方差均为1，即=1；部分探测及干扰信道系数的方差均为0.005，即=0.005；同时，通信信道系数的方差设置为1，即=1。针对近距离IRS，双功能阵列与IRS之间的信道状态优于双功能阵列与探测目标之间的信道状态，对此，本节分析=0.01与时雷达与通信性能。最后，迭代停止常数为ε=0.01。

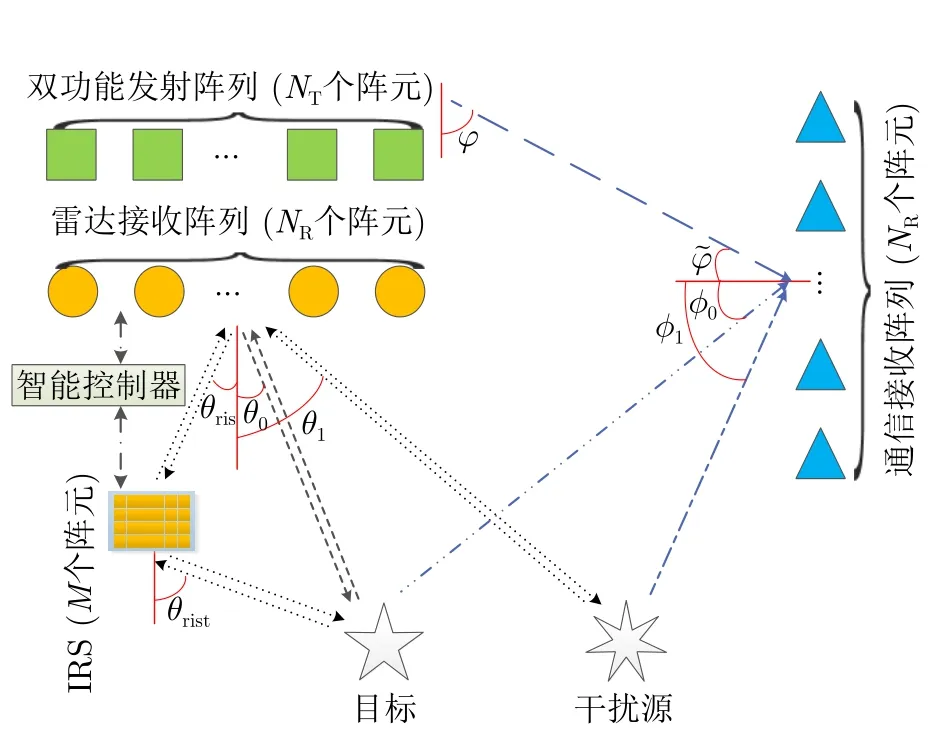
图2 I-DRC多载波波形设计的仿真场景Fig.2 Simulation scenario of multi-carrier waveform design for I-DRC

由于所提ADM算法是在方向图调制信息嵌入技术基础上，本节分析了ASK-IE[34],QAM-IE[36]与ADSRP[38]算法的性能以便对比ADM算法。QAM-IE算法的基本原理是在保持雷达主瓣增益前提下，控制指向通信用户方向的旁瓣幅度与相位(对应一个通信符号)，通信接收端通过解调接收信号，进而判断对应的通信符号。QAM-IE算法的待优化问题为

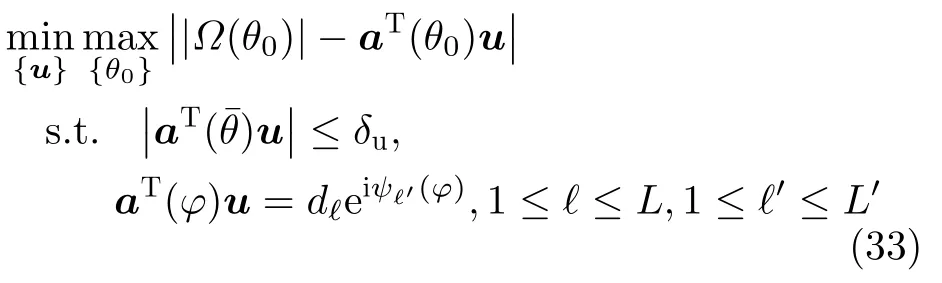
其中，Ω(θ0)为理想波束方向图；ψℓ′(φ)为指向通信方位角的L′种可能旁瓣相位之一。优化问题的求解过程详见文献[36]。ASK-IE算法为QAM-IE算法不考虑相位信息ψℓ′(φ)的特例。两种算法均采用单载波波形且没有考虑I-DRC雷达与通信耦合问题(即没有考虑WEP约束，对应ADM算法在=1时的情形)。ADSRP算法通过联合优化发射与接收波束以最大化雷达探测性能(在特定WEP需求下)，详细过程请参考文献[38]。

图3展示了由ADM算法获得的L=2个发射波束。可以看出，两个波束在方位角θ0=0◦及θris=15◦的幅度相同，表明两个波束的雷达性能相同。通信方位角φ=40◦的旁瓣幅度彼此不同，即d1=−10 dB和d2=−20 dB；在脉冲持续时间内，通信接收阵列处判断发射波形的旁瓣幅度，进而确定其所对应的通信符号。此外，在方位角θ1=60◦处有零陷点，意味着ADM算法可有效降低干扰源对雷达性能的影响。

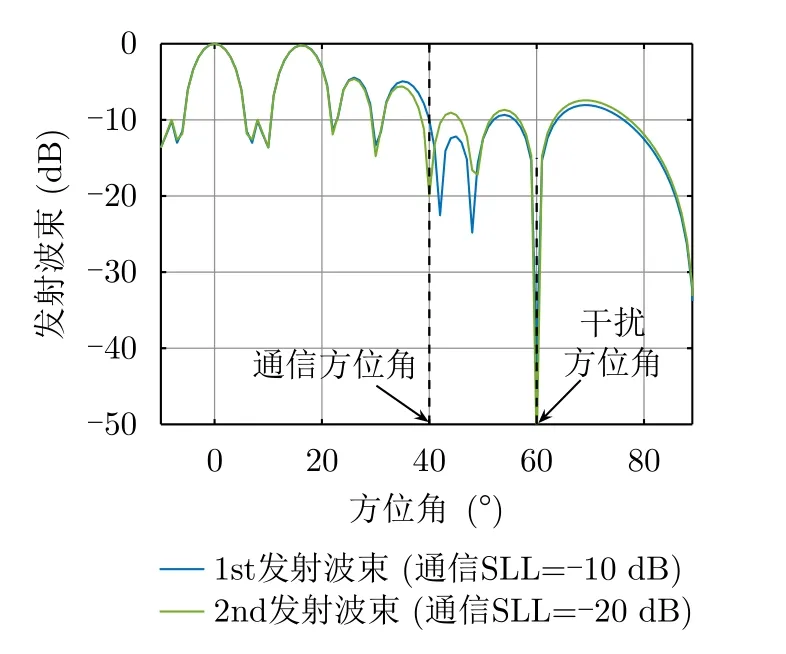
图3 通信方位角旁瓣幅度分别为–10 dB和–20 dB的发射波束Fig.3 Transmit beampatterns with sidelobe amplitudes of–10 dB and–20 dB,respectively,towards the communication direction

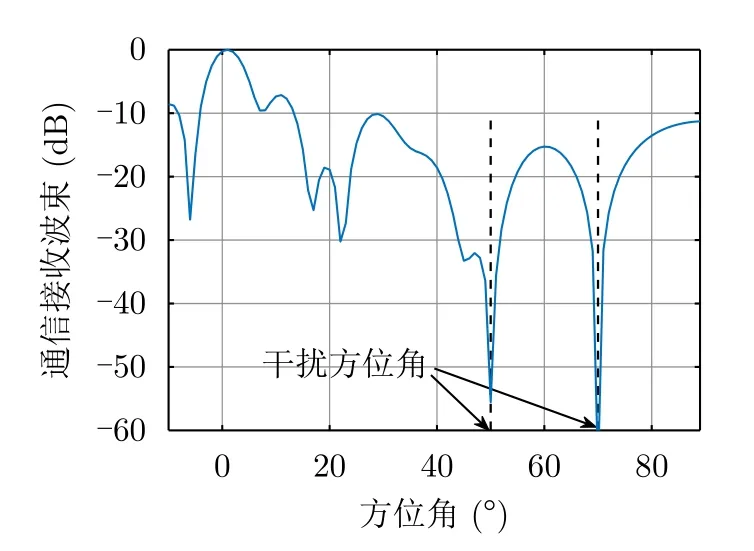
图4 通信接收波束Fig.4 Receive beampattern of communication

基于图5所示子载波信道状态，接下来分析不同WEP要求下I-DRC多载波波形功率分配方案。从图5可以看出，部分子载波(如子载波9和13)雷达信道状态较好，有利于雷达探测。部分子载波(如子载波1和5) IRS信道状态较好，有利于经由IRS发射单元进行目标探测。部分子载波(如子载波6、9和15)通信信道状态较好，有利于通信符号的传输。干扰子载波1和5以及通信干扰子载波2、3和4的信道强度较强，对应子载波上传输的信号将对雷达(或通信)性能造成相对强烈的干扰。

图5 子载波信道状态Fig.5 Channel condition of subcarrier

图7展示了不同WEP要求下RMI随着发射总功率变化曲线图。可以看出，RMI随着发射总功率的增加单调递增。对比无WEP约束、=10−4与=10−54种情形，无WEP约束时RMI值最大，这是因为传输功率仅根据雷达信道状态自适应地分配。同时，WEP要求越高，RMI越小；这是因为功率分配过程需兼顾雷达与通信子载波信道状态，功率被相对“均匀”地分配到各个子载波，造成RMI值的减小。对比图7(a)和图7(b)(或图7(c)和图7(d))可知，越大，RMI值越大，即I-DRC探测性能越好。对比图7(a)和图7(c)(或图7(b)和图7(d))可知，相较于ADSRP算法，ADM算法可获得更高的性能增益。这是因为ADM算法性能同时受到直接探测信道与IRS信道状态的影响，可以根据两者的信道状态进行自适应分配；然而，ADSRP算法的性能仅由直接探测信道状态决定。当直接探测信道状态较差时，ADSRP算法的RMI值较小，而ADM算法的RMI值由IRS信道状态决定。

图8展示了ADM,ADSRP,ASK-IE和QAM-IE算法RMI性能比较。可以看出，相较于ASK-IE和QAM-IE算法，ADM算法可获得更大的RMI值，即更好的雷达性能(ADM与ADSRP算法性能比较已在图7详细分析)。这是因为ASK-IE和QAM-IE算法仅优化发射波束形成矢量，而ADM通过联合优化发射与接收波束形成矢量获得了更高的增益。此外，ASK-IE和QAM-IE算法的RMI值相同，这是因为两者均是在不影响雷达性能前提下将通信符号嵌入到雷达波形里，差别仅为ASK-IE算法没有考虑旁瓣相位信息。

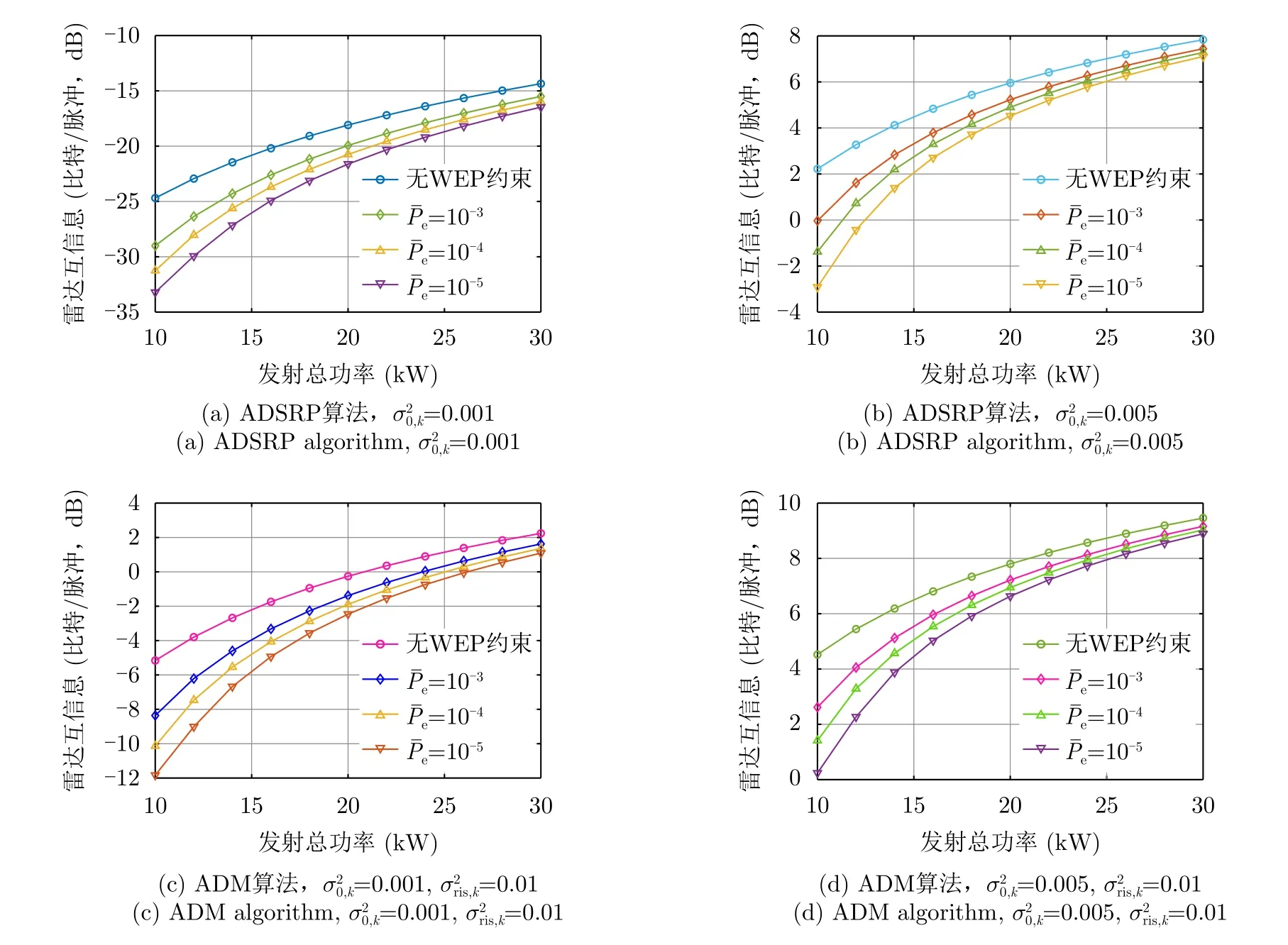
图7 不同WEP要求下RMI随着发射总功率变化曲线图Fig.7 Curve of relationship between RMI and total transmit power under different WEP requirements

图8 ADM,ADSRP,ASK-IE和QAM-IE算法RMI性能比较Fig.8 RMI Performance comparison for ADM,ADSRP,ASK-IE and QAM-IE algorithms

图9展示了ADM,ASK-IE和QAM-IE算法的WEP随着信噪比变化曲线图(L′=4)。可以看出，与ASK-IE和QAM-IE算法相比，所提的ADM算法能更好地对抗噪声、获得更低的WEP。这是因为基于ADM的多载波波形优化算法在相同条件下获得更高的可达速率，引起各个子载波上符号空间中符号之间距离的增加。

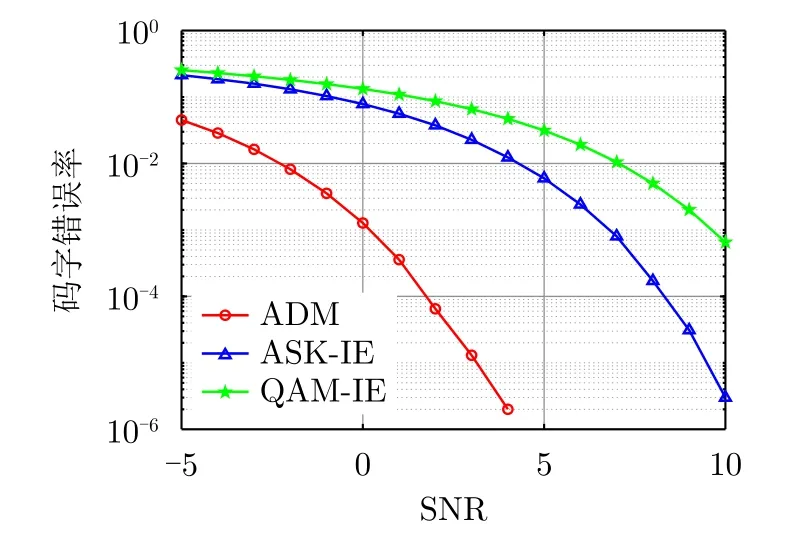
图9 WEP随着信噪比变化曲线图(L′=4)Fig.9 Curve of relationship between WEP and SNR (L′=4)

5 总结

本文研究了I-DRC系统的多载波波形优化问题，构建了传输功率、WEP、旁瓣幅度以及IRS反射系数约束下RMI最大化模型，提出了基于ADM的多载波波形优化算法。该算法将原高维非凸优化问题分解为传输功率、WEP与旁瓣幅度约束下双功能发射波束形成矢量设计子问题、IRS反射系数优化子问题、雷达与通信接收波束形成矢量设计子问题，进而获得其等价松弛凸问题/局部解析解并进行迭代优化，获得了多载波波形功率分配策略的局部最优解。仿真实验验证了ADM算法能同时实现雷达与通信功能并有效提升了RMI和WEP；同时，近距离IRS能显著提升I-DRC的探测性能。

由于IRS应用于雷达系统以及雷达通信双功能系统的公开文献较少，同时受限于研究条件、时间以及文章篇幅，本文有诸多问题值得进一步研究和完善，包括但不限于以下6个方面：

(1) 文中没有考虑地球曲率和地面障碍物等因素。对此，受到地球曲率和地面障碍物影响后的通信距离、中断概率等通信指标性能需要进一步探讨。

(2) 文中所提算法复杂度受到子载波、阵元数以及所传输符号数决定，当三者数目较大时算法复杂度会急剧上升，无法满足实时性要求。对此，需要进一步降低算法复杂度。

(3) 文中所获得结果均在目标方位角及CSI已知的基础上；然而，实际场景中无法精确获得目标方位角及CSI。对此，需要进一步研究目标方位角以及CSI非理想估计情形下I-DRC系统的探测与通信性能。

(4) 文中所提算法没有约束雷达主瓣和通信接收阵列方向之外的旁瓣电平，而高旁瓣电平将导致系统性能下降。对此，约束雷达主瓣和通信接收阵列方向之外的旁瓣电平情形下的探测与通信性能有待研究。

(5) 文中忽略了近距离IRS受到的电磁干扰，而在干扰较强时，IRS的存在可能会降低系统性能[43]。对此，需要进一步分析IRS受到电磁干扰时I-DRC的系统性能。

(6) 文中仅研究了近距离IRS，远距离IRS情形下I-DRC系统性能需要进一步探讨。