频率捷变雷达联合模糊C均值抗间歇采样干扰

董淑仙 吴耀君 方文 全英汇

(西安电子科技大学电子工程学院 西安 710071)

1 引言

在雷达信号处理领域，干扰与反干扰一直是一个研究热点[1–3]。尤其是数字射频存储器(Digital Radio Frequency Memory,DRFM)的出现和发展，给雷达系统带来了严峻挑战[4–7]。DRFM通过对截获到的信号进行调制和转发，利用干扰与雷达发射信号的相参特性，在雷达匹配滤波后产生逼真的假目标，且一般情况下干扰的能量远大于目标的能量，严重影响雷达对目标的有效检测[8,9]。

为了对抗基于DRFM产生的欺骗干扰，频率捷变体制雷达应运而生[10–12]。文献[10]将频率捷变技术应用到多输入多输出-合成孔径雷达(Multiple-Input Multiple-Output Synthetic Aperture Radar,MIMO-SAR)以对抗欺骗干扰，提高雷达的生存能力。文献[11]将脉间频率捷变体制应用到引信工作，通过设置频率快速跳变，使得干扰机难以瞬时追踪和复制引信信号，解决无线电引信在基于DRFM的欺骗式干扰环境下的目标探测问题。由于捷变频体制雷达发射脉间载频随机跳变的脉冲信号，当干扰机对截获信号转发延迟大于一个脉冲重复周期时，干扰信号与雷达接收机的混频信号不再匹配，低通滤波时干扰信号会被滤除。因此，捷变频雷达可以有效对抗DRFM产生的跨脉冲重复间隔(Pulse Repetition Interval,PRI)干扰[13]。

随着间歇采样转发干扰(Interrupted Sampling Repeater Jamming,ISRJ)的提出和发展，传统的基于频率捷变体制雷达的目标检测面临严峻挑战[14–16]。ISRJ通过对截获到的雷达信号进行低速的间歇采样，巧妙利用干扰与雷达发射脉冲信号的相参性，脉冲压缩后，在当前PRI内产生与目标相似的假目标，形成脉内干扰，使得频率捷变技术失效。为了对抗ISRJ干扰，文献[17]提出一种基于时频分析的ISRJ抑制方法，结合ISRJ的时域不连续转发特性，时频分析后在时间维搜索能量函数的极小值点并结合此点对应的频域设计带通滤波器，然后对时频分析后的回波信号频域滤波，实现ISRJ的抑制。由于该方法主要是对ISRJ在时域不连续的部分进行提取，对抗高占空比的间歇采样重复转发干扰时算法性能下降明显。文献[18,19]通过脉内频率编码实现脉内不同子脉冲之间的相互掩护，从而可以对未被干扰机采样的信号进行提取，在对抗高占空比的间歇采样重复转发干扰时优势明显。但该方法在抑制干扰时，主要是通过经验设定阈值对子脉冲是否被干扰进行判决，在不同雷达、干扰参数下灵活性较差。

针对上述问题，本文基于ISRJ时域不连续的特性，提出一种基于频率捷变体制雷达联合模糊C均值(Fuzzy C-Means,FCM)的抗ISRJ方法。首先，本文将脉内频率编码技术与传统的捷变频体制雷达相结合，设计雷达发射脉内线性调频(Linear Frequency Modulation,LFM)-频率编码联合调制、脉间载频捷变的脉冲波形；基于脉间频率捷变体制，雷达可以有效对抗跨PRI的ISRJ干扰，对于在当前发射脉冲回波中的ISRJ干扰，接收机接收到回波信号后，设置与脉内频率编码相对应的窄带滤波器对回波信号进行窄带滤波，得到不同频率编码对应的子脉冲回波信号；由于干扰机对雷达发射信号是间歇采样，因此，部分子脉冲中含有干扰，部分子脉冲中不含有干扰，只有目标信号和噪声。基于这一特点，本文引入FCM算法对所有脉冲压缩后的子脉冲中是否含有干扰进行判断并对干扰进行抑制；最后将未被干扰的子脉冲进行脉内积累并利用压缩感知(Compressed Sensing,CS)算法进行脉冲间的相参积累，进而计算目标的距离和速度信息，实现目标的检测。

2 信号模型

2.1 脉内频率编码-脉间载频捷变信号模型

在弹载干扰机等诸多应用场合，由于物理尺寸与天线隔离度等条件限制，干扰机采用收发分时的工作模式。因此ISRJ具有时域覆盖不连续的特点。本文基于这一特性，设计雷达发射脉内频率编码-脉间频率捷变的发射波形。脉内频率编码可以实现不同子脉冲之间的相互掩护，脉间载频捷变可以实现不同脉冲间的相互掩护。

假设一个相参处理间隔(Coherent Processing Interval,CPI)内雷达发射N个脉冲波形，每个脉冲内有K个频率编码，第n个 发射脉冲信号的第k个子脉冲表示为

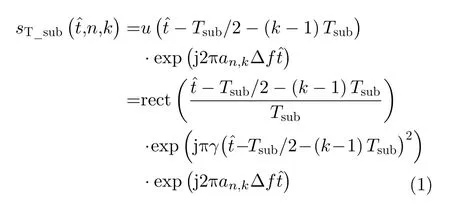
其中，表示快时间，为矩形窗函数，Tsub表示子脉冲的时宽，调频斜率γ=Bsub/Tsub，Bsub表示子脉冲的带宽，an,k ∈{0,1,...,K−1}表示第n个发射脉冲信号的第k个子脉冲的频率调制码字，∆f表示子脉冲间的最小频率间隔。

经上变频调制器处理后，第n个发射脉冲信号可以表示为

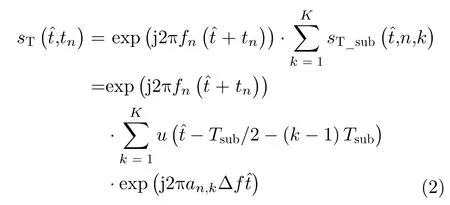
其中，tn表示慢时间，fn=f0+a(n)∆F表示第n个发射脉冲信号的载频，f0表示雷达发射脉冲信号的初始载频，∆F表示脉间跳频步长，a(n)是{0,1,...,M −1}中的随机数，表示发射脉冲信号的跳频序列，M表示跳频点数且M>N。

假设雷达观测场景中有一个目标，初始距离为R0，速度为v，那么该目标的第n个回波信号可以表示为

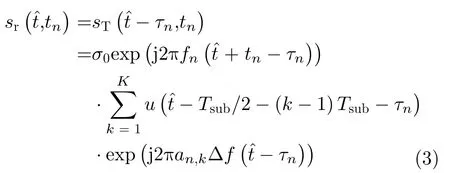
其中，σ0表示目标的后射散向系数，τn=2(R0−v(n −1)Tr)/C表示目标的时延，C=3×108m/s表示光速。

2.2 ISRJ模型

根据转发方式不同，ISRJ可以分为直接转发(Direct Forwarding,DF)、重复转发(Repeat Forwarding,RF)和循环转发(Cyclic forwarding,CF)。此外，为了使干扰具备压制效果，干扰机会对采样信号调制噪声，本文采用的噪声调制方式为噪声调频干扰，是噪声对射频信号进行频率调制产生，表示为

其中，调频噪声信号u(t′)是一个零均值的广义平稳随机过程，KFM为噪声的调频系数，φ0服从[0 2π]均匀分布。

其中，Aj表示干扰信号幅度；Tj表示干扰机采样时长；Ts表示采样重复周期，为干扰机采样和转发时长之和；P=[Tp/Ts]表示采样次数；τj表示干扰时延。

同理，假设干扰机重复采样信号为p2(t)，基于噪声调制的间歇采样重复转发干扰(ISRJ-RF)可以表示为

其中，Q=[Ts/Tj]−1为间歇采样重复转发的次数。

因此，雷达接收机接收到的第n个回波信号可以表示为

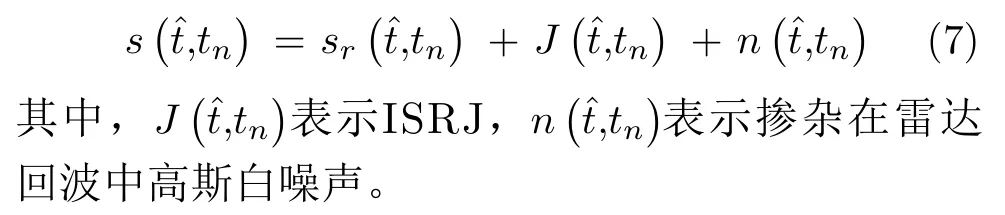
3 干扰对抗

图1为本文所提算法的具体流程。

图1 所提方法的流程图Fig.1 Flow chart of the proposed method

3.1 频域窄带滤波与分段脉冲压缩

由于间歇采样转发干扰具有时域不连续的特点，发射信号中只有部分子脉冲被采样转发。根据所设计的雷达发射脉冲信号采用脉内频率编码调制，在雷达接收机处，设置窄带滤波器对下变频调制器处理后的回波信号进行频域滤波，得到不同频率编码对应的子脉冲回波信号，然后进行脉冲压缩处理。其中，频域滤波的带通滤波器组的参数由频率调制码字和子脉冲带宽等确定。第n个回波信号第k个子载波对应的带通滤波器Bn,k(f)可以表示为

窄带滤波具体步骤为：首先通过快速傅里叶变换(Fast Fourier Transform,FFT)将第n个回波信号变换到频域；然后根据式(8)设置的窄带滤波器对进行频域滤波；最后将频域滤波后的信号进行逆快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)，即可得到对应于第n个雷达发射信号第k个子脉冲的时域回波信号：

3.2 基于FCM算法的干扰判决与抑制

3.2.1 FCM算法

FCM是属于机器学习领域的一种典型的非监督分类算法[20,21]。该算法通过优化函数计算每个样本对所有类中心的隶属度来自动实现样本分类，且最终划分到同一类别内的样本之间的相似度最大，不同类别的样本之间的相似度最小[22]。

假设待分类的样本集为X={x1,x2,...,xZ}，Z表示样本数目，类别数目为c，cj表示第j类的聚类中心，j=1,2,...,c,uj(xi)表示样本xi相对于第j类的隶属度且。FCM算法目标函数为

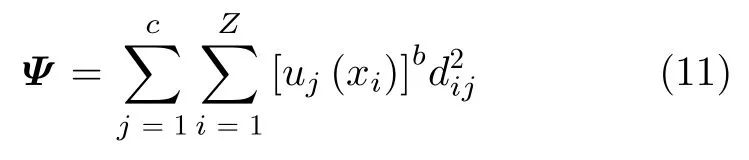
其中，b表示模糊加权指数，一般情况下，取值为2；dij=‖xi−cj‖表示样本xi到第j类的聚类中心cj的欧几里得距离。从式(11)可以看出目标函数Ψ实质上计算的是各样本到聚类中心的加权欧式距离平方和，其值越小，表明样本依附聚类中心越紧致。

通过对式(15)和式(16)迭代计算，实现对样本隶属度uj(xi)和类别聚类中心cj的更新。当样本的隶属度变化小于设定阈值时，停止迭代计算。最后，样本xi的分类结果由式(17)决定

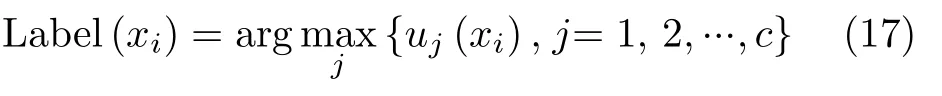
3.2.2 基于FCM算法进行干扰判决

基于干扰机天线收发分时的特点，本文所设计脉内频率编码发射波形可以实现不同子脉冲之间的相互掩护。因此，窄带滤波后部分子脉冲中含有ISRJ，而部分子脉冲中只含有目标和噪声。为了达到欺骗和压制的效果，干扰能量一般都远大于目标信号的能量。因此，脉冲压缩后，含有干扰的子脉冲和不含有干扰的子脉冲的均值和方差都有差异，且含有干扰的子脉冲的均值和方差大于只含目标和噪声的子脉冲的均值和方差[18,19]。本文从该角度出发，基于子脉冲脉冲压缩后的均值和方差特征，利用FCM算法对子脉冲是否含有干扰进行判断。具体步骤如下：

步骤1 分别计算y中每个子脉冲取模值后的均值和方差，并记为mean(n,k)和var(n,k)，n=1,2,...,N,k=1,2,...,K，完成特征提取。

步骤2 将均值和方差两个特征组合为一个样本(mean(n,k),var(n,k))，得到样本集X={(mean(1,1),var(1,1)),(mean(1,2),var(1,2)),...,(mean(N,K),var(N,K))}。

步骤3 使用FCM算法进行样本分类。具体为：

步骤3.1 设置待分类的类别数c；

步骤3.2 用0～1的随机数初始化隶属矩阵U，其中U的行数等于数据集X中的样本数量(N ×K)，列数等于类别数c，矩阵U中的第i行第j列的数值uj(xi)表征了第i个样本对第j类的隶属度，且满足每个样本对所有类别的隶属度总和等于1，即

步骤3.3 初始化迭代次数h=1，并记初始化隶属矩阵U0=U；

步骤3.4 结合式(16)计算j个聚类中心cj，j=1,2,...,c；

步骤3.5 根据式(15)更新隶属矩阵Uh；

步骤3.6 判断更新后的隶属矩阵是否满足‖Uh −Uh−1‖<ε,ε为设定的阈值。如果不满足，令h=h+1，重新进入步骤3.4；如果满足，则结束迭代，进入步骤3.7；

步骤3.7 结合最终计算得到的隶属矩阵和式(17)得到对样本集X的分类结果。

步骤4 干扰判决。比较c个聚类中心的均值和方差特征，判断均值和方差最小的聚类中心所在的类别为不含干扰的子脉冲，其他聚类中心所在的类别为含有干扰的子脉冲；

步骤5 干扰抑制。将含有干扰的子脉冲作置零处理，得到ISRJ抑制后的子脉冲

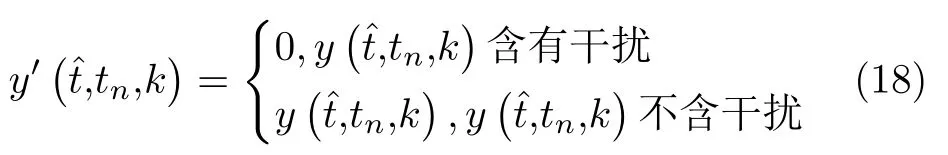
经过上述抗干扰算法处理后，含有干扰信号的子脉冲回波会被剔除，只留下含有目标回波和噪声的子脉冲回波。接下来，对干扰抑制后，第n个脉冲重复间隔内的子脉冲信号进行脉内积累：

其中，An,k表示第n个雷达发射信号第k个子脉冲脉冲压缩后目标信号的幅值，表示脉内积累后的噪声。可以看出，干扰抑制后，信号主要包括目标回波脉压后的包络幅值项与脉间载频项。由于脉间载频的跳变，一个CPI内方位向相位关系混乱，本文通过构造与目标距离-速度参数相匹配的字典矩阵，利用CS算法实现多个脉冲间的相参积累。

4 基于CS算法的捷变波形相参积累

一般情况下，经过干扰抑制后，一个距离单元内的目标个数较少，即目标场景具有稀疏性，因此可以采用基于CS理论的稀疏重构算法进行脉间相参积累[23–25]。将雷达观测场景内感兴趣的距离-速度范围进行离散化，设离散化后的距离维、速度维格点数分别为L,W，使

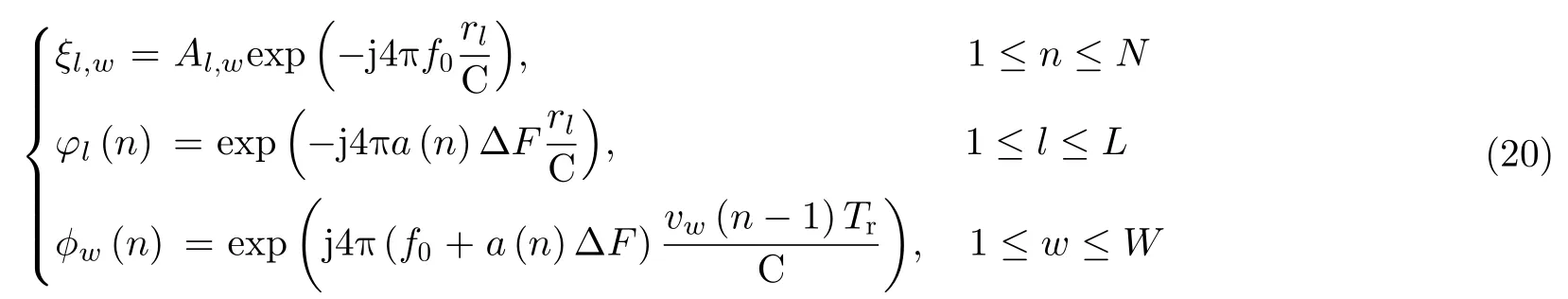
其中，ξl,w表示目标的后向散射系数，φl(n)和ϕw(n)分别表示距离和速度相位项。进而可以构建字典矩阵

其中，el,w=[φl(1)×ϕw(1)φl(2)×ϕw(2) ...φl(N)×ϕw(N)]T。则式(19)所示的回波信号可以重新改写为

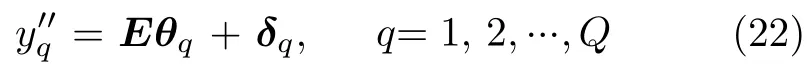
其中，δq表示噪声向量，θq表示待求解的第q个距离单元的稀疏重构向量，θq的估计值可以通过求解如下ℓ1范数优化问题得到

根据稀疏重构向量θq可得到目标的距离和速度信息，实现对目标的检测。

5 仿真结果与分析

为了分析本文设计的脉内LFM-频率编码联合调制、脉间载频捷变波形的多普勒容限和验证所提算法对ISRJ的对抗性能，本文设置5组实验：(1)仿真分析本文设计波形的模糊函数，进而得到该波形的多普勒容限；(2)仿真分析所提算法对噪声调制ISRJ-DF的对抗效果；(3)仿真分析所提算法对噪声调制ISRJ-RF的对抗效果；(4)设置蒙特卡罗实验次数为100，仿真分析在不同信噪比(Signal to Noise Ratio,SNR)和干信比(Jamming to Signal Ratio,JSR)条件下，FCM算法对被干扰子脉冲的判决正确率；(5)设置蒙特卡罗实验次数为100，仿真分析在不同干扰机采样时长Tj情况下，本文所提算法和文献[19]算法对ISRJ-DF的对抗性能。

实验中，假设干扰机前置目标2000 m，工作频段为13～15 GHz；目标初始距离R0=12 km，速度v=80 m/s；雷达脉内频率编码序列采用10位科斯塔斯(Costas)编码，Costas=[1 2 4 8 5 10 9 7 3 6]，表1为雷达波形的相关参数，雷达发射脉冲信号的时频图如图2所示。

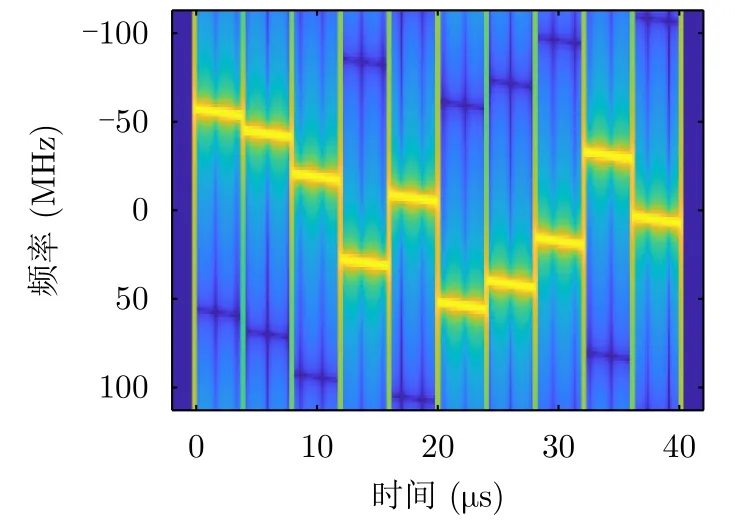
图2 雷达发射脉冲信号时频图Fig.2 Time-frequency diagram of radar transmitted pulse signal

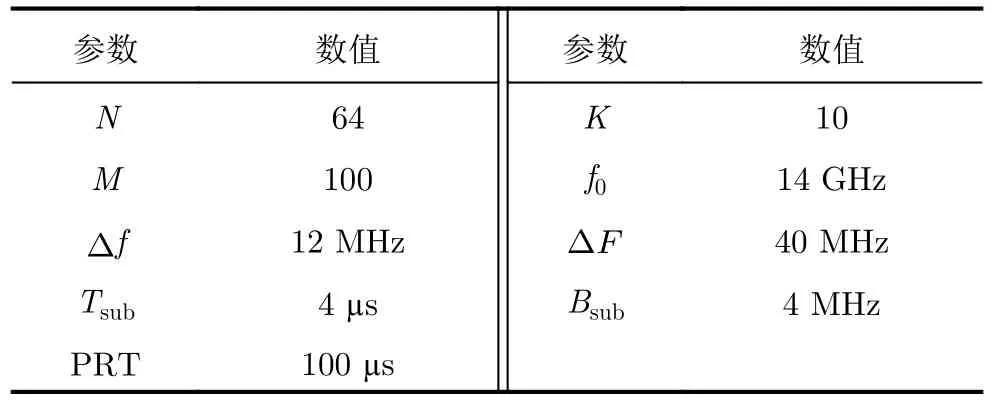
表1 雷达参数Tab.1 Radar parameters

5.1 仿真实验1

图3为本文所设计的脉内LFM-频率编码联合调制、脉间载频捷变波形的模糊函数图，可以看出，模糊图近似“图钉型”，因此具有较高的分辨力。

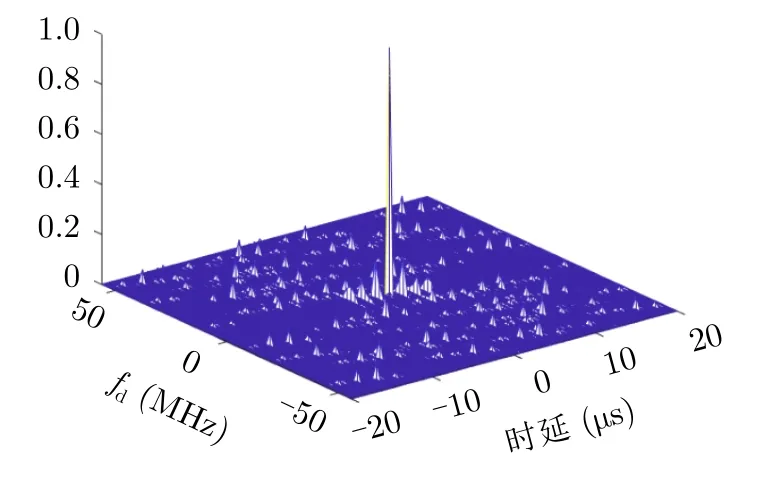
图3 本文设计波形的模糊函数图Fig.3 Ambiguity function diagram of the waveform designed in this paper

为了分析设计波形的多普勒容限，设置蒙特卡罗实验次数为100，多普勒频率fd=0～100，分别计算fd取值不同时距离模糊图的主旁瓣比(Main Sidelobe Ratio,MSR)，得到图4所示的曲线。可以看出，随着fd的增大，MSR先是基本不变，然后呈下降趋势。当fd=0时，MSR获得最大值19.01 dB，当fd=80 Hz时，MSR约为15.84 dB。相比于fd=0的MSR，fd=80 Hz时MSR下降了大约3.17 dB，因此，设计波形的多普勒容限大约为80 Hz。

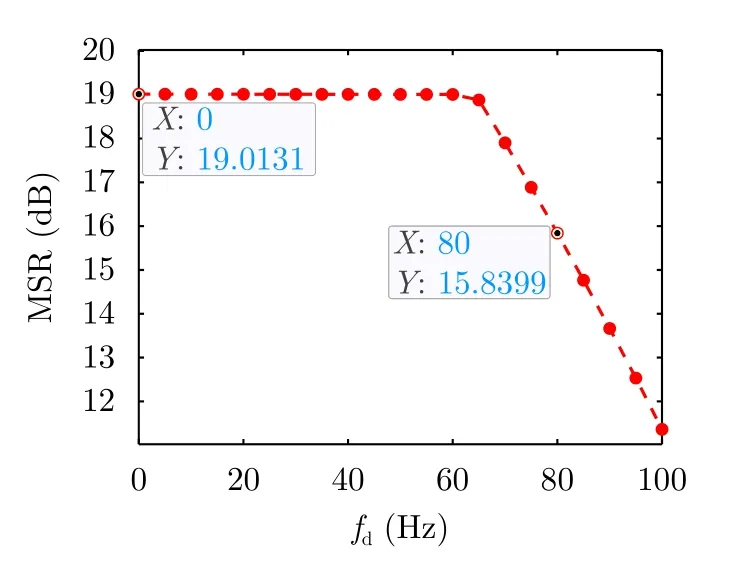
图4 多普勒频率与距离模糊图主旁瓣比的关系曲线Fig.4 Relationship curve between Doppler frequency and the main sidelobe ratio of distance fuzzy graph

5.2 仿真实验2

噪声调制ISRJ-DF参数设为：干扰机采样时长Tj=4µs，采样重复周期Ts=8 µs，噪声调频带宽Bj=4 MHz，调频系数KFM=Bj/2.35，子脉冲压缩后信噪比SNR=15 dB，干信比JSR=30 dB，干扰机对雷达信号同步采样转发，即干扰机的开始采样位置为雷达发射脉冲信号的开始位置。由于本节干扰机采样时长Tj和子脉冲时宽Tsub相同，部分子脉冲被干扰机完全采样，部分子脉冲未被干扰机采样。回波信号窄带滤波后，子脉冲主要有两种情况，因此，在使用FCM算法设置待分类的类别数目c=2。

图5为所提方法对ISRJ-DF的对抗效果图。图5(a)为含有ISRJ-DF的雷达回波的时域图，可以看出，雷达发射信号被干扰机采样5次，且干扰的能量大于目标信号的能量，目标被干扰和噪声淹没。图5(b)为含有ISRJ-DF的雷达回波的时频图，可以看出，基于ISRJ时域不连续的特点和脉内频率编码的优势，有5个子脉冲没有被干扰机采样，可以在频域窄带滤波后，用于目标检测。图5(c)和图5(d)分别为窄带滤波后含有ISRJ-DF和不含有ISRJ-DF子脉冲的脉冲压缩结果，由于ISRJ-DF与雷达发射脉冲信号是相参的，在脉冲压缩步骤获得了积累增益，形成了具有强能量的假目标干扰，影响雷达对目标的正确检测；而从图5(d)可以看出，未被采样的子脉冲在频域窄带滤波和脉冲压缩后，可以得到目标信息。使用FCM算法对子脉冲是否含有ISRJ进行判决并将干扰抑制后，对一个脉冲内的未被干扰的子脉冲进行脉内积累，得到图5(e)所示的结果。最后使用二维高分辨稀疏重构算法对雷达观测场景进行重构，得到图5(f)所示的仿真结果，可以看出，计算得到目标距离为12 km，速度为80.67 m/s，根据速度分辨率计算公式∆v=C/(2f0·N ·PRT)≈1.7 m/s，仿真速度误差0.67 m/s在允许范围内。

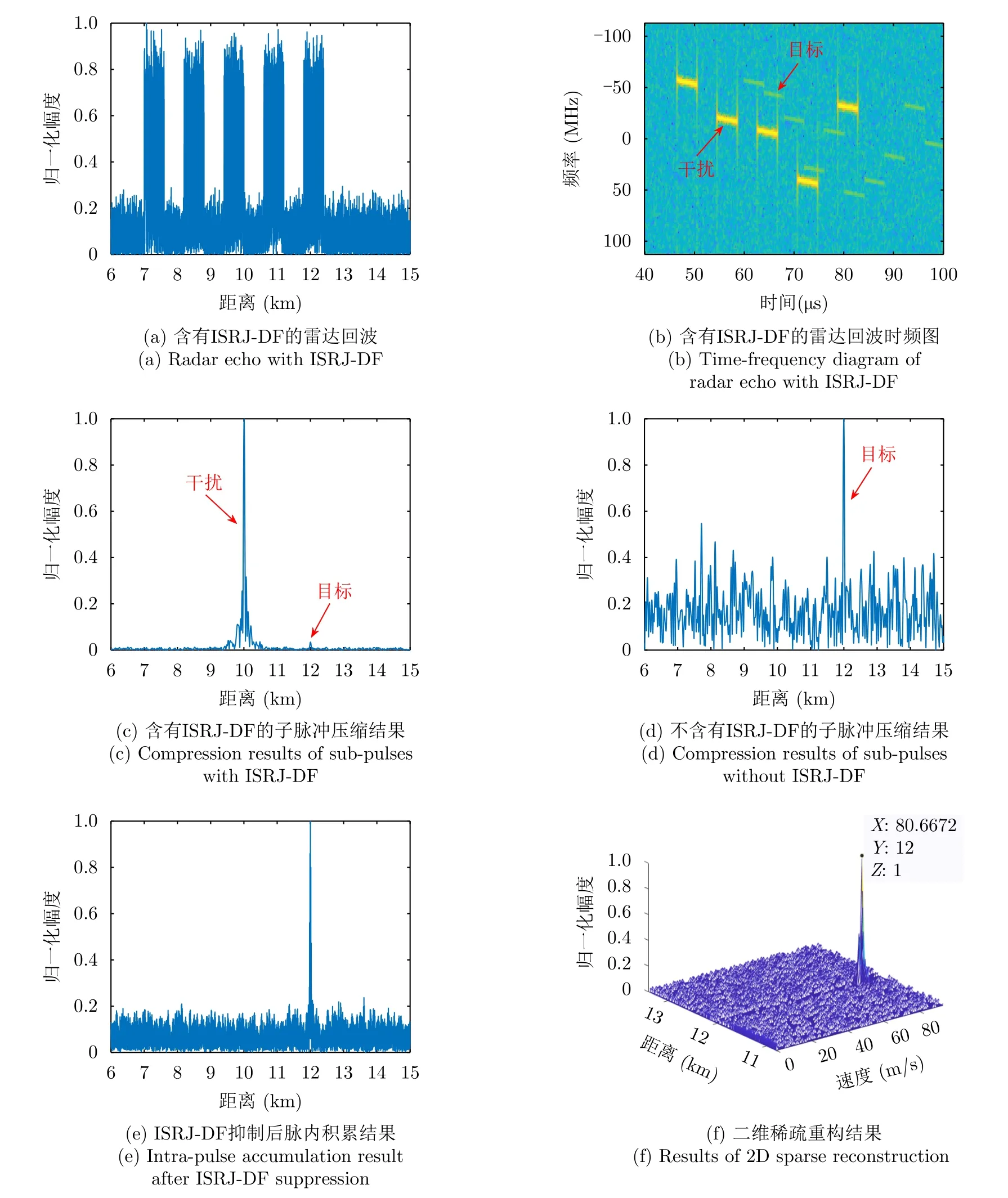
图5 所提方法对ISRJ-DF的对抗效果图Fig.5 Antagonistic effect diagram of the proposed method against ISRJ-DF

5.3 仿真实验3

为仿真分析所提方法对噪声调制ISRJ-RF的对抗效果，设置干扰机采样时长Tj=4 µs，采样重复周期Ts=12 µs，其余参数设置与仿真实验2相同。根据图1所提算法流程对含有噪声调制ISRJ-RF的回波信号进行处理，得到图6所示的仿真结果。其中，图6(a)和图6(b)分别为含有ISRJ-RF的雷达回波时域图和时频图，从图6(a)可以看出，雷达信号被采样4次，且每次采样后转发的时宽是ISRJ-DF的两倍，说明干扰机间歇采样雷达信号后在时域重复转发了两次。图6(c)和图6(d)分别为窄带滤波后含有ISRJ-RF和不含有ISRJ-RF子脉冲的脉冲压缩结果，从图6(c)可以看出，由于ISRJ-RF的转发次数为2，子脉冲脉冲压缩后，产生了两个逼真的假目标干扰，雷达无法对目标正确检测；而图6(d)为干扰机未采样的子脉冲的脉冲压缩结果，可以用于目标的检测。与对噪声调制ISRJ-DF的处理流程相同，计算所有脉冲压缩后子脉冲的均值和方差特征，并基于这两个特征用FCM算法对子脉冲是否含有ISRJ-RF进行判决和抑制。然后，对未被干扰的子脉冲进行脉内积累，得到图6(e)所示的仿真结果，可以看出，ISRJ-RF已经被抑制，只剩下目标信息。图6(f)为使用二维稀疏重构算法进行目标检测的仿真结果，计算得到目标距离为12 km，速度为80.67 m/s，与仿真实验1计算得到的目标距离、速度信息相同。

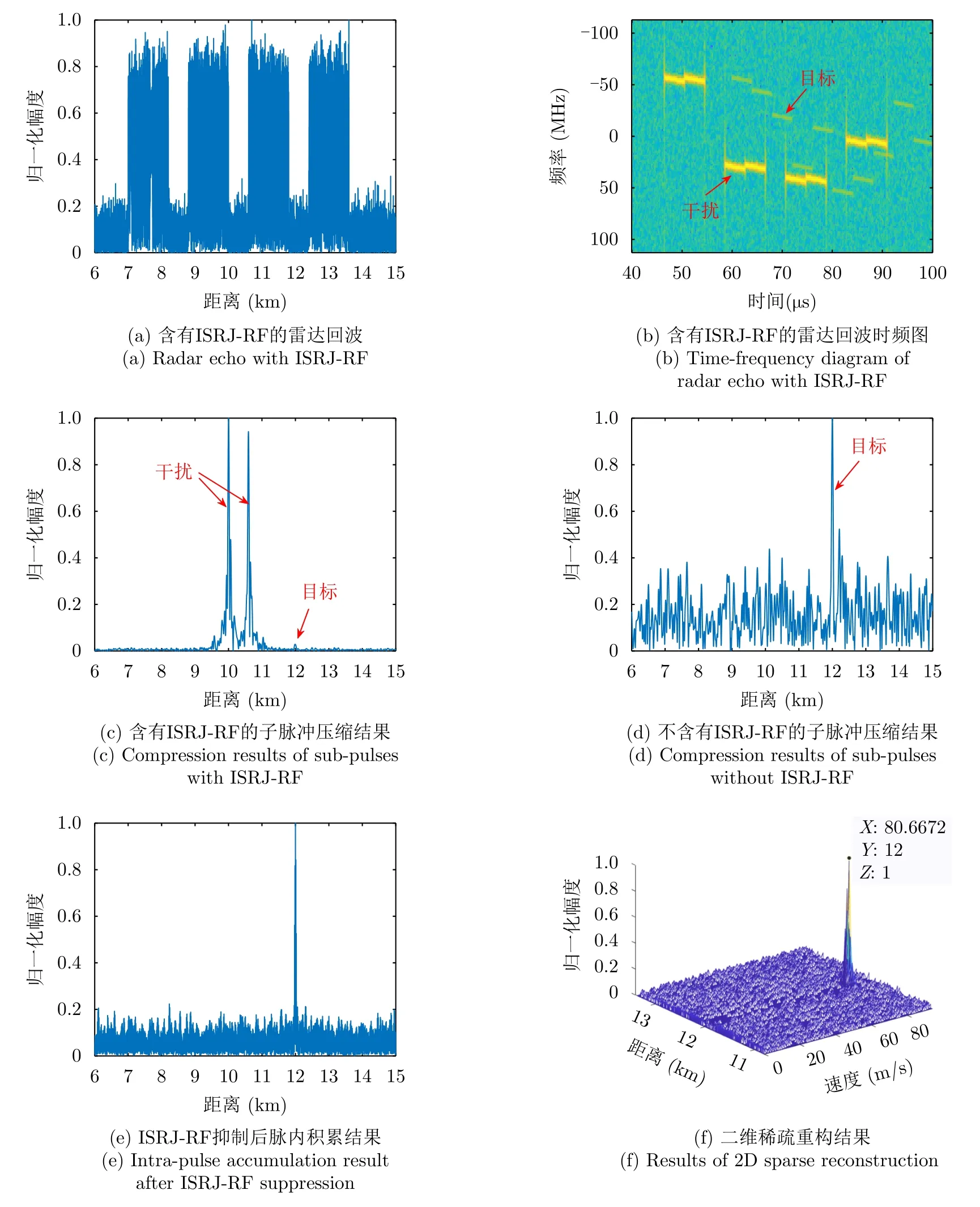
图6 所提方法对ISRJ-RF的对抗效果图Fig.6 Antagonistic effect diagram of the proposed method against ISRJ-RF

5.4 仿真实验4

为了仿真分析在不同干信比JSR和信噪比SNR条件下，FCM算法对ISRJ-DF和ISRJ-RF的判决正确率，设置干信比分别为JSR=5 dB,10 dB,20 dB,30 dB，子脉冲压缩后信噪比SNR为–6～20 dB，根据本文所提算法进行仿真，得到图7所示的关系曲线。从图7(a)和图7(b)可以看出，当SNR和JSR都比较小时，FCM对两种ISRJ的判决正确率均小于100%。这是因为此时噪声能量较强，不仅目标被噪声淹没，干扰也被噪声淹没，统计的均值和方差特征中噪声能量占主导地位，不能对含有干扰的子脉冲准确判决。当SNR比较小但JSR=30 dB时，FCM对两种ISRJ的判决正确率均达到100%。这时从未被干扰的子脉冲统计的均值、方差特征中噪声能量占主导地位，而从被干扰的子脉冲中统计的均值、方差特征是干扰的能量占主导地位，由于干扰能量大于噪声能量，FCM算法可以基于两者的能量差异对含有干扰的子脉冲进行准确判决。当SNR比较大时，4种JSR条件下，FCM对两种ISRJ的判决正确率均达到了100%。此时，从未被干扰的子脉冲统计的均值、方差特征是基于目标的能量，被干扰的子脉冲统计的均值、方差特征是基于干扰的能量，FCM算法可以基于干扰与目标的能量差异对含有干扰的子脉冲进行准确判决。

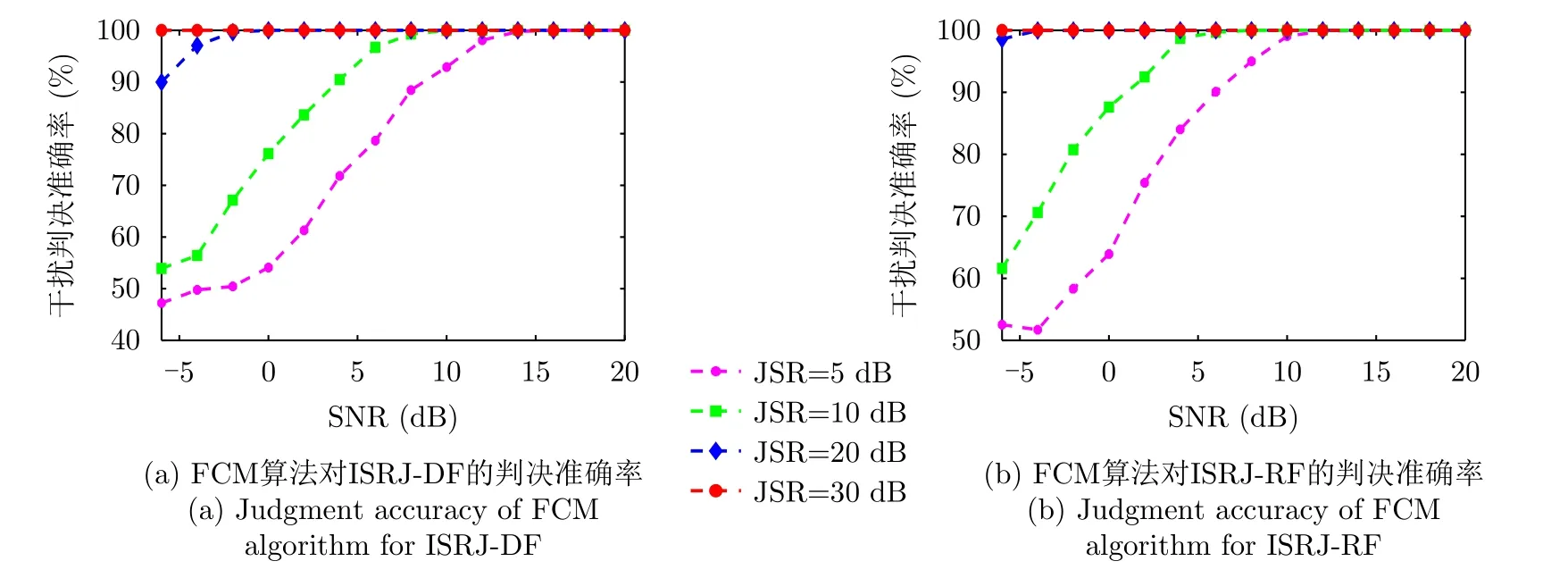
图7 不同信噪比下FCM算法对ISRJ的判决准确率Fig.7 Judgment accuracy of FCM algorithm for ISRJ under different SNR

5.5 仿真实验5

下面仿真分析在不同干扰机采样时长Tj情况下，分别使用本文所提算法和文献[19]算法对ISRJDF进行判决与抑制，以二维稀疏重构后输出信干比(Signal to Jamming Ratio,SJR)作为对干扰抑制性能的对比。其中，设置FCM算法中待分类的类别数分别为c=2,3,5,7，也就是将数据集X分别分为2,3,5,7类。当干扰机采样时长Tj不是子脉冲Tsub的整数倍时，不同子脉冲被干扰机间歇采样的程度不同，导致分段脉压后不同子脉冲的均值方差特征存在差别，因此，需要将待分类的类别数设置为c ≥2，并判断均值和方差最小的聚类中心所在的类别为不含干扰的子脉冲，其他聚类中心所在的类别为含有干扰的子脉冲。文献[19]是通过结合干扰门限因子和子脉冲脉冲压缩后的方差特征对子脉冲是否被干扰进行判决，本文参考文献[19]在对比实验中设置干扰门限因子ρ=0.5。设置Tj/Tsub=1～2，输入SJR=−30 dB，100次蒙特卡罗仿真实验如图8所示。

图8 二维稀疏重构后不同算法的输出信干比Fig.8 Output SJR of different methods after 2-D sparse reconstruction

从图8可以看出，当干扰机采样时长Tj是子脉冲时宽Tsub的整数倍时，两种算法均可以对子脉冲是否含有干扰进行有效判决，二维稀疏重构后可以获得较高的SJR。当干扰机采样时长Tj不是子脉冲时宽Tsub的整数倍时，不同子脉冲被采样的时间长度存在不同，部分子脉冲未被采样，部分子脉冲被不完全采样，部分子脉冲被完全采样。因此，脉冲压缩后，不同子脉冲之间的均值和方差特征差别较大。在使用FCM算法对子脉冲是否含有干扰进行判决时，需要设置合适的待分类的类别数，以对不同采样程度的子脉冲进行分类，从而有效判决出未被干扰的子脉冲以用于目标检测。从图8可以看出，当分别设置待分类的类别数c=2,3,5,7时，所提算法在c=7时获得了较好的输出SJR，说明设置较大的待分类类别数更有助于对子脉冲是否含有干扰进行判决。另外，从图8可以看出，当干扰机采样时长Tj不是子脉冲时宽Tsub的整数倍时，大多数情况下，所提算法在c=7时获得了比文献[19]更高的输出SJR，说明相对于文献[19]根据经验设置干扰门限因子，本文所提算法更具有灵活性。

6 结论

针对传统频率捷变体制雷达无法有效对抗ISRJ的难题，本文提出一种捷变频雷达联合FCM的抗ISRJ方法。首先设计一种脉内频率编码-脉间载频捷变的雷达发射波形，以实现脉内不同子脉冲、脉间不同脉冲的相互掩护。对包含ISRJ的回波信号，通过频域窄带滤波、脉冲压缩、特征提取、FCM干扰判决等步骤实现ISRJ的对抗。最后通过脉内积累、脉间二维高分辨稀疏重构实现目标的检测。由于本文是在频域对雷达回波进行分选，在对抗高占空比的ISRJ-RF时，与时间维干扰抑制算法相比，本文所提算法具有明显优势。