接收函数与重力联合估计的技术与应用研究进展

唐晗晗，郭良辉,2*

1 中国地质大学（北京）地球物理与信息技术学院，北京 100083

2 地质过程与矿产资源国家重点实验室（中国地质大学），北京 100083

0 引 言

地壳厚度和泊松比是研究地壳结构和物质组成的重要参数. 其中，地壳厚度可以描述莫霍界面起伏特征和地壳增厚或减薄状态，岩矿石泊松比表示在单向应力作用下横向应变与纵向应变比值的绝对值，可以描述地壳物质的长英质或铁镁质矿物含量及可能的熔融状态（Watanabe et al., 1993;Christensen, 1996）. 在以往的地质、地球物理研究中，众多学者利用这两个参数量化地壳结构、物质成分和变形特征，分析地壳增厚或减薄模式（Dugda et al., 2005; Ji et al., 2009; He et al., 2014;Wang et al., 2016; Cheng et al., 2021）、地壳均衡状态（Wang et al., 2017; Guo et al., 2019），区分构造单元或识别构造块体之间的缝合带（Lombardi et al., 2008; Guo et al., 2019），结合地热数据描述地壳水化状态（Lowry and Pérez-Gussinyé, 2011; Ma and Lowry, 2017）等. 特别地，泊松比在描述物质成分及差异方面有重要的作用，获取精确的地壳泊松比分布将对认识地球构造演化具有重要意义.

远震接收函数H-κ叠加方法（Zhu and Kanamori, 2000）是获取地壳厚度和波速比的重要手段. 该方法避免了因拾取震相到时不准确而引起的误差，被广泛应用于全球多个地区（Lombardi et al., 2008; Ji et al., 2009; Bashir et al., 2011; Liu and Niu, 2011; He et al., 2014; Tao et al., 2014; Zhang et al., 2018）. 然而，实际应用中部分台站下方往往地壳结构比较复杂（如构造界面倾斜、壳内低速层等），以及存在地震波形记录信噪比低等问题，接收函数H-κ叠加方法拾取地壳厚度和波速比参数的不确定性增大. 因此，需要引入其它数据的约束，改善接收函数H-κ叠加谱错乱的问题，降低估计的不确定性.

Lowry和Gussinye（2011）首先提出了接收函数与重力联合估计地壳厚度和波速比参数的方法，该方法认为布格重力异常包含莫霍界面起伏、壳内密度不均匀异常体和壳幔热异常引起局部物质膨胀这三部分引起的重力异常. 主要思路为：（1）利用远震接收函数H-κ叠加法计算目标台站及其附近台站（以目标台站为窗口中心）的地壳厚度和波速比分布；（2）根据接收函数得到的地壳厚度和波速比正演得到区域理论重力异常，与实测重力异常作差并利用似然比（likelihood ratio method, Beck and Arnold, 1977）的方法计算重力H-κ似然谱；（3）根据克里金插值原理计算最优插值概率得到“OI”（optimal interpolations）似然谱，并将其与重力H-κ似然谱、接收函数H-κ谱相乘并作归一化处理，谱峰值对应联合估计的最优解. 该方法综合考虑了地热因素以及周围台站数据分布结果的影响，更精确地对台站下方的地壳厚度和波速比进行了估计，并成功应用到美国西部地区，得到了该地区更可靠的地壳厚度和波速比分布. 随后，该方法经过国内外学者多次的发展和改进，逐步形成了一套相对完备的接收函数和重力的联合估计技术.

本文将对接收函数与重力联合估计的技术原理与应用进展进行概述. 首先，分别简述单一接收函数、重力似然函数估计的方法原理及两者联合估计技术的算法流程；再者，介绍接收函数与重力联合估计的技术进展，分析方法存在的不确定性及其对应的优化和改进；然后，介绍该方法的应用实践；最后，对当前接收函数与重力联合估计方法进行总结，并对其未来研究方向提出展望.

1 接收函数与重力联合估计的原理

1.1 接收函数H-κ叠加法

接收函数是去除震源、地震波传播路径以及仪器响应等因素后的时间序列，它主要记录了地震台站下方地壳和上地幔速度间断面所产生的转换波（如图1，Ps）及其多次波（PpPs, PpSs+PsPs）的信息（Langston, 1979）. 震中距在 30°～90° 之间的远震 P 波可视为垂直入射，其在莫霍面上的转换点对应台站正下方，因此，可以利用接收函数记录的震相计算台站正下方的地壳厚度与波速比.

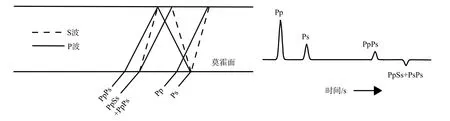
图1 远震P波接收函数示意图Fig. 1 Sketch map of teleseismic P-wave receiver functions

Zhu 和 Kanamori（2000）提出的接收函数H-κ叠加法是目前获取地壳厚度和波速比的使用最广泛的方法，在理想的单层地壳模型下，不同震相的走时差与地壳厚度H、波速（横波VS，纵波VP）关系为：

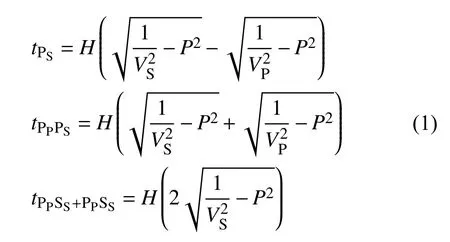
式中，P表示射线参数，通过不同数值的（H,κ）组合，计算每个震相的到时差及其对应的接收函数振幅r（t），赋予不同的权重再求和：

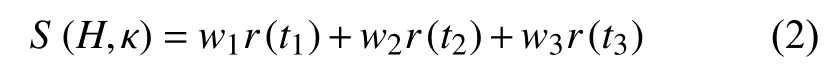
即可得到H-κ叠加图（如图2a所示）. 其中w1、w2、w3为各项权重系数，和为1. 叠加谱值最大点对应的（H,κ）即为最优解.

该方法通过叠加的方式减少数据中非相干噪声的影响，也避免了人工拾取到时引起的误差，具备处理大量地震事件数据等优点. 试验表明，在单层水平均匀地壳模型下，接收函数H-κ叠加结果受相关输入性参数（如初始P波速度、震相的权重分配）的影响较小，准确度较高（Ogden et al., 2019; 查小惠等, 2020）. 但在实际情况中，当台站下方地壳结构复杂（如壳内低速层、界面倾斜等问题的影响），应用接收函数H-κ叠加法估计结果的可靠性降低.

1.2 重力似然估计法

Shi等（2018）在Lowry和Gussinye（2011）的方法基础上，考虑到小面积情况下深源热异常偏弱可以忽略，从而从理论重力异常的正演部分和似然函数的计算部分对重力模块的似然估计法进行了简化. 这里以Shi等（2018）改进后的重力似然估计法为例说明其基本原理.

在不考虑深部热异常影响的情况下，布格重力异常主要包括莫霍界面起伏引起的异常gMoho和壳内密度不均匀体引起的重力异常gCrust（Blakely,1995），其中，地壳厚度可以描述莫霍面的起伏变化，波速比则可以描述地壳内部物质成分差异，与密度参数有一定关联，其各个部分的正演公式可表示为（Shi et al., 2018）：

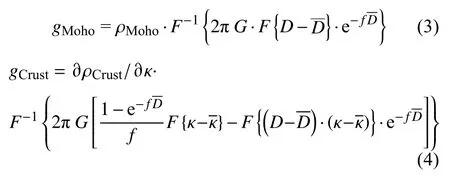
式中，ρMoho为莫霍面上下密度差，∂ρCrust/∂k为地壳密度相对于波速比的变化率，D=H-E为莫霍面深度，H为地壳厚度，E为地形高度，D为研究区莫霍面深度的平均值，κ为研究区波速比的平均值，F{}和F-1{}分别表示傅里叶变换和反傅里叶变换，G为万有引力常数，f为波数. 利用这一关系，就可以将接收函数和重力结合起来.

最大似然估计法是建立在最大似然原理基础上的一种统计方法，在作参数估计的应用中比较常用. 重力似然估计是根据理论重力异常gModel与实测重力异常gObs之间的偏差Δgres计算其似然值，进而分析其正演模型的准确程度. 假设实测重力异常和理论重力异常的残差服从高斯分布，则其似然函数可表示为均值µ 和方差σ2的函数：

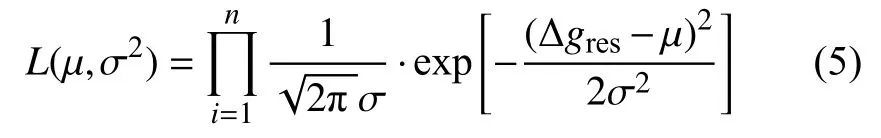
据此，通过设定同接收函数H-κ叠加谱一样大小和步长的H值和κ值，进行扫描并计算每个点的似然函数值，就可以得到重力H-κ似然谱（如图2b所示），其最大值即对应重力估计的地壳厚度和波速比参数. 通常重力H-κ似然谱的谱条带与接收函数H-κ叠加谱的谱条带呈正交或交叉关系.

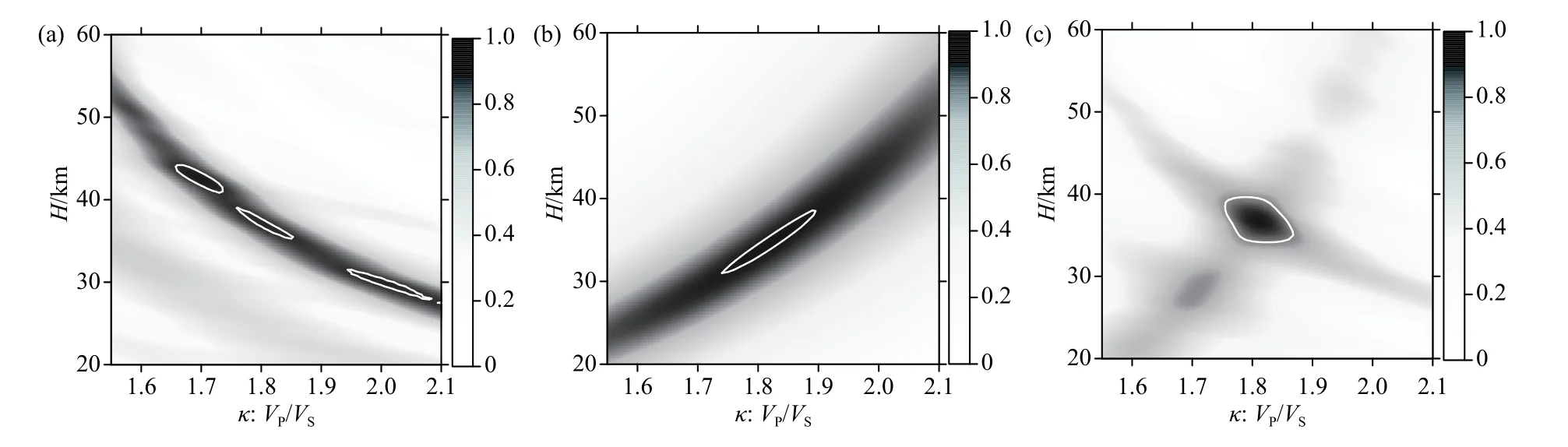
图2 （a）接收函数H-κ叠加谱；（b）重力H-κ似然谱；（c）联合H-κ叠加谱Fig. 2 （a） H-κ map from the receiver-function H-κ stacking; （b） H-κ likelihood map from the gravity inversion；（c） H-κ map from the joint inversion

1.3 接收函数与重力联合估计算法与流程

在接收函数与重力联合估计的算法流程中，重力模块的计算是在一个以目标台站为中心的窗口内进行的，联合估计算法流程图见图3（本节流程对应实线流程框），具体步骤为：

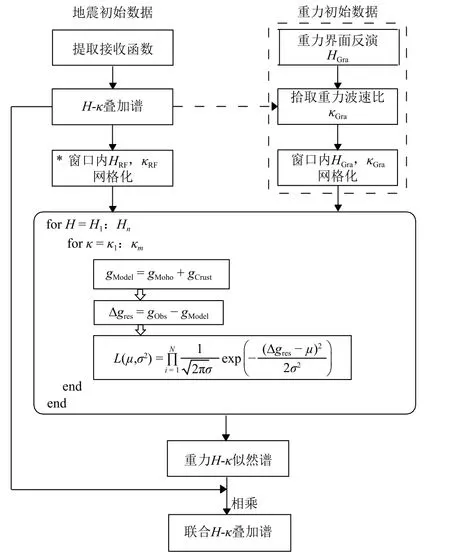
图3 接收函数与重力联合估计算法流程图. 实线流程框对应接收函数结果作初始数据，将虚线流程框替换星号框（*）即对应重力结果作初始数据Fig. 3 Flow chart of the joint estimation by receiver function and gravity data. Shapes in solid line refer to the algorithm when receiver function results are initial data.Substitute the shape marked with an asterisk （*） for shapes in dashed line, which refers to the algorithm when gravity results are initial data

（1）准备初始模型数据. 利用常规接收函数H-κ叠加方法获取研究区内所有台站的地壳厚度和波速比分布，并将地壳厚度减去地形得到莫霍面深度数据，作为重力异常正演的初始模型数据.

（2）计算密度参数ρMoho和∂ρCrust/∂k. 准备研究区的布格重力异常数据，并将研究区所有台站的地壳厚度和波速比结果插值成与重力数据坐标相对应的网格数据，根据公式（3）和（4）采用线性回归算法计算ρMoho和∂ρCrust/∂k的数值.

（3）计算重力H-κ似然谱. 将窗口内所有台站的接收函数结果网格化，结合第（2）步得到的ρMoho和∂ρCrust/∂k密度参数分别进行正演[公式（3）和（4）]，求和即可得到窗口内的理论重力异常.同时，截取该窗口内的实测重力异常，两者作差，代入似然函数[公式（3）]计算其似然值；然后，扫描同接收函数H-κ叠加谱一致的H、κ范围和步长，计算每组（H,κ）对应的似然值，最终生成重力H-κ似然谱.

（4）获取目标台站下方（H,κ）的联合估计值. 将计算得到的重力H-κ似然谱与接收函数H-κ叠加谱相乘，并作归一化处理，得到联合估计谱（图2c），谱值最大点所对应的坐标（H,κ）即为联合估计的最优解.

（5）将获取的目标台站结果（H,κ）对初始模型数据进行更新，重复上述步骤计算下一个台站的联合估计值，直到遍历研究区内所有的台站.

1.4 质量评价

接收函数H-κ叠加谱图提供了评估方差最大值的置信区间. 目前单一和联合估计技术均采用常规的误差分析方法（Zhu and Kanamori, 2000），对s（H,κ） 震相谱进行泰勒展开并略去高阶项，得到地壳厚度和波速比的方差Ea√ton等（2006）在此基础上将振幅谱方差σs改进为，使得方差的大小会随叠加地震事件数目n的增加而降低，更符合叠加规律.

2 接收函数与重力联合估计的技术进展

自从Lowry和Pérez-Gussinyé（2011） 提出接收函数与重力联合估计的方法以来，多位学者在该方法的发展与应用实践中对算法做了分析和优化改进，主要针对：初始模型的构建、相关密度参数的估计、地幔热异常的影响、地壳结构复杂（如沉积层的存在）情况下的算法等，促进技术实用化.

2.1 初始地壳模型优化构建

联合反演对初始模型数据（地壳厚度H和波速比κ）具有依赖性，国内外学者一般使用接收函数H-κ叠加法得到的地壳厚度和波速比（H,κ）作为重力异常正演的初始模型数据. 但在实际应用中，常规接收函数H-κ叠加法的结果往往连续性较差，模型网格化后易形成局部异常值，导致重力异常的拟合效果不佳，不符合残差呈高斯分布的假设. Shi等（2018）对接收函数估计结果异常的台站，研究采用接收函数与重力联合建模的办法，优化选取台站的初始地壳厚度和波速比参数. 我们将这一初始地壳模型构建办法推广到全区，这是因为该方法得到的初始地壳模型较为平滑，有利于后续重力异常拟合. 这种初始模型优化构建算法的基本原理如下：

对布格重力异常进行分离，得到反映莫霍界面起伏引起的区域异常部分，然后应用频率域密度界面反演方法（Oldenburg, 1974）对该部分重力异常进行反演，得到莫霍面深度数据，此时再加上地形值，就得到新的初始地壳厚度HGra. 将重力反演得到的台站地壳厚度HGra投影到台站的接收函数H-κ叠加谱图上，此时最大值对应的κ值作为新的初始地壳波速比κGra. 按照这种办法可获取研究区内所有台站的初始地壳厚度和波速比参数（HGra, κGra），实现全区的初始地壳模型优化构建. 本小节对应流程图（图3）的虚线流程框部分（将星号框替换为虚线流程框，即为重力结果作初始模型数据的完整联合估计流程）.

2.2 滑动窗口参数优化选取

马亚伟（2017）对该方法进行参数测试，评估计算窗口对联合估计结果的影响，得出以下认识：计算窗口的网格间距对联合反演结果的影响不大，但为提高运算速度，建议窗口内网格间距N与台站平均间距M的关系为M/4＜N＜M；不同的窗口大小会对地壳厚度和波速比的结果产生一定误差，误差范围分别在1 km和0.02之内，为保证频率域计算的稳定性，应保证结果在合理范围内适当增加窗口大小. 同时，对计算窗口的大小进行说明：台站分布较密的区域对应的计算窗口较小，台站稀疏的区域对应的计算窗口较大，须确保每个窗口内至少有5个地震台站. 陈国江（2020）在此基础上对实际台站的窗口大小进行调试，测试台站为NM.BHS和LN.GAX，计算窗口的网格间距为20 km，固定ρMoho和∂ρCrust/∂k均为400 kg/m3，分别进行了步长为40 km、变化范围从200～600 km的窗口测试.结果显示窗口太大或太小均会导致联合反演拾取的结果不稳定（误差在±1 km和0.02之间），并认为在实际数据处理过程中，使计算结果稳定的窗口大小应设置在300～450 km范围之间.

2.3 地幔热异常压制

本文在1.2节中介绍了Shi等（2018）不考虑地幔地热因素，对重力异常的正演和拟合作出简化，并采用重力最大似然估计法代替似然比（Beck and Arnold, 1977），完成了重力H-κ似然谱的求算. 当研究区域较小，深部地幔热变化引起的重力异常较小且平缓，因此，该方法对小面积研究区是适用的.

对于较大面积的研究区，Guo等（2019）研究使用重力垂直梯度异常gz代替布格重力异常进行联合估计算法改进，此时公式（3）、（4）变为：

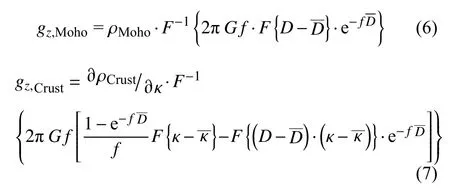
梯度异常的优点是能够削弱深部背景场，且突出浅部场源的影响，因此一定程度上可以压制深部地幔地热变化引起的重力异常，使得接收函数与重力联合估计方法在较大面积研究区得以推广应用，具有更广的适用性.

2.4 密度参数优化估计

为了测试密度参数ρMoho和∂ρCrust/∂k对联合估计值的影响，陈国江（2020）利用实测台站数据（NM.BHS和LN.GAX）对这两个参数进行测试，结果显示，莫霍面上下密度差ρMoho对联合反演结果的影响较小，ρMoho在100～600 g/cm3范围内变化，联合反演的估计值基本保持不变；地壳平均密度与波速比的偏导数∂ρCrust/∂k在100～1 600 g/cm3范围内变化时，两个台站的结果展示出不同的变化规律，NM.BHS不受该参数的影响，而LN.GAX在200 g/cm3以内变化对联合估计结果（H,κ）产生影响，大于200 g/cm3之后结果基本保持不变. 因此，∂ρCrust/∂k参数对不同台站结果的影响不同，具体规律还须进一步明确.

密度参数∂ρCrust/∂k表示地壳平均密度与波速比的偏导数，可以用来指示地下主要岩石类型的密度与波速比的相关变化关系. Lowry和Pérez-Gussinyé（2011）利用重力异常反演计算得到美国西部的∂ρ/∂κ为460 kg/cm3，Zhang等（2020）根据相关系数法计算得到的美国西部∂ρ/∂κ为1 180 kg/cm3，中东部为300 kg/cm3. 可知，该参数的不确定性较大，使用一个常数代表一个地区是不合适的，需要计算∂ρ/∂κ的二维分布. 为此，我们对密度参数∂ρCrust/∂κ的估计做了理论分析和算法改进，以适应研究区不同构造单元参数值差异的实际情况.

Ji 等（2009）在实验室下测量主要岩石类型的平均密度和波速比，发现两者存在相关变化关系.我们研究发现密度参数∂ρCrust/∂κ的绝对值对应这一变化趋势线的斜率大小、及∂ρCrust/∂κ的正负指示密度和波速比两个参数的正负相关关系. 因此，可以利用地壳视密度和平均波速比的分布计算∂ρCrust/∂κ的横向变化值. 我们定义其绝对值∂ρ/∂κ=，其中Δρx和Δρy指地壳视密度在水平x、y方向的变化（Δκx和Δκy同理），如果某一点的视密度与波速比同时高于或低于区域平均值（如2 670 kg/m3和 1.75），该点∂ρ/∂κ取为正，反之，∂ρ/∂κ取负. 为了保证∂ρ/∂κ参数分布的平滑性，可以采取计算周围一定范围内的平均值并进行滑动窗口的方式.

通常，密度参数∂ρCrust/∂κ的变化范围在-1 600～1 600 kg/cm3范围之间（零值除外），在盆地地区以负值为主，指示较高的密度背景值；在山脉地区以正值为主，指示较低的密度背景值.

2.5 地壳结构复杂情况下的算法优化

本文在1.1节提到，在单层、水平均匀的地壳模型假设下，接收函数H-κ叠加结果受初始P波速度数值的影响较小（Ogden et al., 2019; 查小惠等,2020）. 在实际情况中，部分台站下方不满足这一理想假设，呈多层或介质不均匀等复杂结构，此时，地壳初始P波速度的错误估计会对接收函数的叠加结果产生扰动，进而对联合估计结果产生影响. 为了减少地壳初始P波速度带来的误差，任志远和李永华（2020）在接收函数和重力联合估计的基础上加入面波频散的约束，获取台站下方地壳平均P波速度、地壳厚度与波速比值.

此外，模型测试和实际应用发现，在沉积层较厚的地区，联合估计的效果不佳，因此，联合估计技术还应对考虑沉积层的影响. 目前，前人在接收函数的沉积层校正方面提出了一些方法（Yeck et al., 2013; Tao et al., 2014; Yu et al., 2015），我们把沉积层校正技术（Yu et al., 2015）与接收函数和重力的联合估计技术结合起来，用以削弱沉积层的影响，此时，重力异常增加了沉积层底界面起伏引起的重力异常gSed，对应的正演公式为：

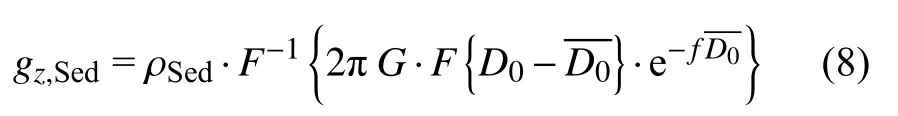
式中，ρSed表示沉积层界面上下密度差，D0和D0表示沉积层深度及其平均值. 此时，联合估计得到的地壳厚度和波速比结果指示沉积层下方的结晶基底结构，因此，考虑沉积层的影响有助于获取台站下方真实的地壳结构.

3 接收函数与重力联合估计的应用进展

接收函数与重力联合估计技术可以获取更可靠的地壳厚度和泊松比（以及波速比），为区域地壳变形、物质组成和动力学机制提供重要依据，目前已被应用于北美大陆和中国部分地区.

3.1 美国大陆

岩石类型、温度和是否存在结合水是地壳受力变形和发生破裂的重要影响因素（Lowry and Gussinyé, 2011）. Lowry和Pérez-Gussinyé （2011）利用接收函数、重力和地表热流联合估算了美国西部的地壳厚度和波速比分布，结果发现，波速比低值和岩石圈高温二者与科迪勒拉山脉的变形具有惊人的相关性，利用波速比对温度不敏感、但对石英丰度非常敏感的特性，分析认为，大陆岩石中最弱的矿物——地壳石英的丰度可能是大陆的温度和变形的决定性参数，韧性应变首先位于相对较弱的石英质地壳内，然后促进变暖、水化和进一步弱化，形成一种反馈机制，进一步解释构造活化和威尔逊旋回（Wilson tectonic cycle）. Ma和Lowry （2017）将接收函数与重力联合估计技术应用在美国大陆地区，分析认为水化作用降低了地壳波速比和密度，并在地壳浅层释放热量，而在最底层吸收热量，进一步分析认为科迪勒拉山脉高热流可能反映了部分地壳水化. Zhang等（2020）利用联合估计技术中得到的理论重力异常与实测重力异常之间的偏差，反演并发现了美国中部密苏里州的布卢姆菲尔德附近相邻台站间的深成岩体（bloomfield pluton），该结果与Ravat等（1987）使用重、磁数据构建的复杂密度异常体相一致. 由此可见，联合估计技术获取的重力异常残差还可以帮助识别相邻台站之间的密度异常体.

3.2 青藏高原东南缘

李永东等（2017）通过接收函数与重力联合估计技术估算了青藏高原东南缘的地壳厚度和波速比分布，该地区的地壳厚度整体位于30～60 km之间，由南向北逐渐增厚；地壳平均波速比在1.70～1.86之间变化，相比单一接收函数的结果，联合反演后的结果分布更为均匀，四川盆地及攀西裂谷地区为明显的波速比高值异常，滇南地区呈现出相对的低值异常. 结合水对地壳常见矿物波速比的影响，李永东等（2017）认为青藏高原东南缘的低波速比、低强度特征与俯冲的岩石圈脱水及上覆岩石圈的水合作用有关. 从矿物学角度分析，水的出现会促使地壳中石英、长石等相对较轻的矿物增长，辉石、石榴子石的含量降低，从而降低地壳波速比和密度数值，在重力均衡的作用下地表必然会被抬升，这一过程可能在青藏高原的隆升及变形中扮演着重要角色.

3.3 青藏高原东北缘

石磊等（2020）利用青藏高原东北缘及邻区布设的密集流动地震台阵得到的远震事件数据，结合区域重力异常资料，应用接收函数与重力梯度联合估计方法，获得了青藏高原东北缘及邻区的地壳厚度和波速比参数值及分布特征，结果显示：该地区地壳厚度位于39～65 km之间，由西南向东北逐渐变薄；地壳平均波速比整体呈低值分布，大致在1.71～1.78之间变化. 在此基础上计算得到的艾里均衡深度显示，在松潘—甘孜和西秦岭地区下方出现了最大9.3 km的偏差，这两个地区的莫霍面深度与高程的相关性较弱，说明其均衡补偿的贡献不仅来自地壳，也来自岩石圈深部的地幔. 同时，地壳厚度与波速比、地壳厚度与密度之间存在较强的负相关关系，支持上地壳均匀增厚或下地壳分层的假设.

3.4 华南地区

Guo等（2019）在华南大陆地区应用接收函数与重力联合反演技术，获取了该地区地壳厚度和泊松比的分布. 结果显示：该地区地壳厚度位于26.1～46.5 km之间，整体呈西北厚东南薄的变化特征，沿着宜昌—吉首—百色一线呈现南北向的地壳厚度梯级带，与重力梯级带大致吻合；其均衡地壳厚度表明，扬子块体的地壳超过了均衡深度，补偿过剩，江南造山带和华夏大部分地壳未达到均衡状态，补偿不足. 地壳泊松比显示，大部分地区的数值在0.20～0.31之间，西北部四川盆地及周边地区泊松比大于0.28，推测其前寒武纪基底内可能存在镁铁质中基性火山岩；东部沿海火山区较高，在0.26～0.29之间；扬子块体和华夏地块之间的江南造山带为明显的低值条带，大致在0.20～0.24之间，其低值异常的原因可归结为江南造山带逆冲推覆构造和南华裂谷系沉积. 同时，该低值条带可能指示板块碰撞拼合的位置，Guo等（2019）根据其低值分布，结合相关地质、地球物理资料推测扬子与华夏两块体之间的缝合带位于石台—九江—吉首—百色一线和绍兴—江山—萍乡—永州—贵港—北海一线之间.

3.5 华东地区

我们将接收函数与重力联合估计方法进一步应用在中国大陆华东地区，结果显示，华东地区的地壳厚度位于26.6～62.4 km之间，整体呈现由西向东逐渐变薄的趋势，与地形呈镜像关系. 地壳厚度的梯级变化带与重力梯级带存在相似性和差异性，两者在大兴安岭—太行山—武陵山一线展布相似，在秦岭—大巴和雪峰山一带偏离较大. 该地区地壳平均泊松比范围为0.18～0.31，高泊松比主要集中在沉积盆地及火山地区，四川盆地和鄂尔多斯盆地的基底显示出与正磁异常相对应的高泊松比条带，结合岩石物理数据推测与壳内中基性岩体的侵入有关；松辽盆地北部呈高泊松比异常，推测与新生代以来多期次的岩浆喷发有关. 低泊松比主要位于华北克拉通北部，渭河地堑、江南造山带沿线附近，与构造块体相对应，利用泊松比低值可以指示构造板块的边界位置的这一特点，我们结合前人地质资料，推测中亚造山带东段增生带的延伸位置主要位于白云矿区—化德—赤峰—辽源—和龙一线和苏尼特右旗—林西—通辽—吉林—汪清一线之间.

以上研究表明，接收函数和重力联合估计地壳厚度和波速比的研究工作得到了较快发展，随着方法的不断改进，应用地区涉及了中国大陆和美国大陆，且获得了更可靠的地壳结构，能够为区域地壳结构、物质组成及演化过程提供准确的地球物理依据.

4 结语与展望

接收函数与重力联合估计方法经过不断发展和技术改进，能够适用于地壳结构较为复杂以及地热数据短缺的地区，具有较广的应用前景. 该方法可以获得台站下方较为可靠的地壳厚度和波速比参数，为我们了解地壳结构、物质组成及其动力学演化等方面提供地球物理依据.

然而，接收函数与重力联合估计技术目前仍然存在一些问题，比如，在台站分布稀少的地区，重力异常的拟合残差较大，以及地壳各向异性结构和地震事件方位角的变化对接收函数产生的影响是否可以通过重力约束作用完全消除等，是目前待解决的问题. 同时，该方法目前的误差评估仅是对解的分布区间进行分析，还需要从更多角度（如初始数据、相关密度参数和计算窗口引起的扰动）对联合估计技术误差作全面评估.

该方法可以获得较为可靠的地壳厚度和泊松比分布，考虑到泊松比在描述地壳物质组成方面具有重要价值，今后可以与地质、岩石物理资料相结合，推进区域岩性的识别与分析，更好地发挥其作用.

致谢

感谢中国地震局地球物理研究所李永华研究员、石磊副研究员的有益讨论和宝贵建议. 衷心感谢两位匿名评审专家提出的宝贵意见.