创生修正，体验积淀——王圣昌老师《正方形数的秘密》一课赏析

□ 苏 娜 王圣昌

（1.浙江省温州市实验小学 325000 2.清华大学附属中学朝阳学校 100027）

学习不应停留在对知识的表层理解与机械式重复训练中，教师要基于知识的内在结构和整体特性，以知识为载体，以问题为主线，引导学生从知识学习走向思维发展。“许多时候学生在数学课堂上表现得消极与被动，是因为教师没有引领学生真正学会用数学的眼光看世界，学生在课堂上只能静坐、听从、接受，进行各种训练，没有自主思考的时间。”[1]王圣昌老师执教的《正方形数的秘密》一课，让学生自主经历创新修正的过程，在体验中积累经验、积淀智慧，给一线教师带来了深刻的启示。

该课的目标定位是：利用学具操作，可视化理解（a+b）2≠a2+b2，并在“形”的帮助下自主探索，深入理解为什么（a+b）2=a2+2ab+b2。王老师把目标拆解成精准有效的任务，通过学习、操作、交流、修正，让学生慢慢体验“式”与“形”的内在联系，进而主动表征（a+b）2和a2+2ab+b2的意义。掌握这一知识本身不是教学的目的，而是教学的载体，通过这一载体让学生经历建构模型的过程，是本节课真正的价值所在。

【教学片段赏析】

（一）借助学具，初步建立“式”与“形”的联结

课堂上，教师为每位学生都准备了可以相互连接的不同颜色的小立方体学具。教学伊始，简单的课前交流后，教师在屏幕上呈现了第一个活动任务“请思考如何用学具表示2×（2+3）”。

师：看屏幕上的活动要求，有不明白的地方吗？

生：可以直接表示2×5吗？

生：不可以，因为2+3分开表示，说明它们不是一组的，如果表示成5的话，就变成一组了。

师：非常好！还有问题吗？没有，那就开始吧！

（学生独立操作学具后，教师引导学生进行交流）

师（呈现生1、生2 的作品，如图1、图2）：哪个比较符合题目的要求？

图1 生1的作品

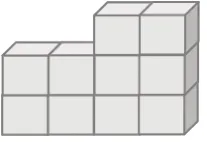
图2 生2的作品

生：我觉得生2 的作品比较符合要求。生1 的作品可以直接用算式2×5表示，生2的作品可以用算式2×2+2×3表示。

生3：我觉得生2的作品也不合适，题目要求用学具表示2×（2+3），生2 的作品没有表示出这个算式的意思来。我认为应该这样（出示自己的作品，如图3）。

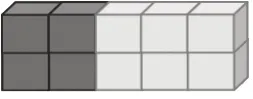
图3 生3的作品

师：谁能看懂他的意思？你同意哪一个？

生：我同意生3的，他用不同的颜色表示，左边深色的表示的是2×2的意思，右边浅色的表示的是2×3的意思，合起来就表示出算式2×2+2×3的意思。

生：我也同意生3 的，一行有（2+3）个小立方体，有2行，所以是2×（2+3）。

学生进入真正的思考状态，是学习发生的重要标志。教学要呈现知识本身的属性，还原学习的本质，让学生更多地经历知识的形成过程，发展学生的能力。以上教学片段中王老师巧妙地利用学具资源，把要达成的学习目标设计成合理的学习任务——“如何用学具表示2×（2+3）”。在这一活动中，学生不只是进行了操作，还通过与同伴间的交流，不断发现“式”与“形”的联结点，明晰2×5 和2×2+2×3 的拼搭方式不能够完全表达算式的含义，进而在辨析中找到并理解能够表达2×（2+3）这个算式意义的正确图形。在这个创生修正的过程中，学生既经历了模式的识别，也实现了活动经验的有效积淀，逐渐积累一种思维的方法和经验。

（二）自主操作，尝试辨析式与式的区别

在学生建立了“式”与“形”之间的联结，能够用学具表达算式的意义后，教师提出第二个活动任务“（2+3）2和22+32是否相同？请用学具操作、画图说明或算式解释等方法表达你的想法”。

师：先思考10 秒钟，想想你的答案是什么，你打算怎样说明你的结论，然后开始。你将有5分钟的时间来呈现你的想法。

学生操作后，教师呈现生4的作品（如图4），并在引导学生思考这幅图的意思后，请生4解释。

图4 生4的作品

生4：我的结论是（2+3）2和22+32不相同。我用学具摆图形来说明。我摆的图形可以看作是一个大正方形，它的边长是2+3，所以面积就是（2+3）2。其中右上角正方形的面积是22，左下角正方形的面积是32，所以它们的面积不相同。

生：我来补充。大正方形的面积（2+3）2比其中两个小正方形的面积22与32的和还多出了2 个长方形，也就是多了2×（2×3）。

教师继续出示生5 的作品，引导：有同学也得到了同样的结论，并用这样一幅图（如图5）表示了他的想法。看一看，你有什么想说的？

图5 生5的作品

生：我觉得不能这样表示。虽然看起来总数是一样的，但是图表达的算式的意思不相同。这幅图上半部分表示的意思是2×5，下半部分表示的意思是3×5，合起来应该是（2+3）×5。图中看不到22和32。

师：怎么改能让大家看到（2+3）2和22+32？

生6一边板书（如图6）一边解释：这里是22，这里是32，加起来是22+32，旁边还多出了两个2×3 的长方形。

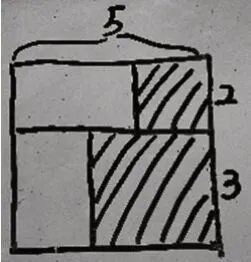
图6 生6的作品

生7：还可以这样画（如图7）。整个图形的面积是（2+3）2，右上是22，左下是32。这和用学具摆差不多，可以更清楚地看出（2+3）2和22+32不相等，多出了两个2×3的长方形。

图7 生7的作品

生8：这样画更清楚，大家看（如图8）……

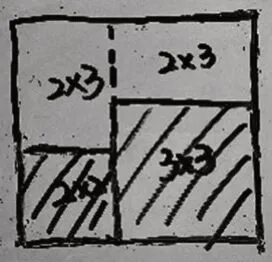
图8 生8的作品

本片段的教学，如果教师只停留在让学生进行（2+3）2和22+32这两个算式的比较上，那么学生也只会就数论数，不知道为什么这样算，根据什么来算，这样算表示什么。而王老师将目标拆解成多个层次的体验式学习任务，让学生针对困惑点“（2+3）2和22+32是否相同”，用学具、图形、算式表达自己的想法，说出自己的理由，注重借助“形”去发现“式”的不同与相同，挖掘数学本质，再在“形”的基础上构建模型。在这个过程中，学生充分经历了“多元表征”“数形结合”的过程，主动倾听、交流、思考，从感知到认知，实现了学习体验的有效积淀。

（三）思考归纳，独立尝试建构模型

在学生借助学具、图形充分感知算式意义的基础上，教师呈现第三个活动任务“请画图表示（2+4）2，并用等式表示（2+4）2=？”。

学生独立写出等式“（2+4）2=22+42+2×2×4”以后，小组内进一步借助图形交流算式中每一个数表达的意思。

本环节中学生对数学知识的“再发现”过程可谓水到渠成。正因为有了之前的小组合作、操作探究、讨论研究等师生间的交往互动，学生的思考逐步深入。他们通过一次次有效的数学活动，在思维碰撞、表达反思、抽象总结的过程中，真正理解了算式的含义。

【对小学数学课堂教学的启示】

知识的习得不能仅通过填充、记忆、巩固练习来完成，教师的教学应关注学生的理解，让学生在获得每一个结论之前都经历深入观察、思考、质疑、操作、验证、总结的“再创造”过程。分析王老师的课，可以在以下几个方面给一线教师的课堂教学带来启示。

（一）有效拆解，让操作路径清晰明了

数学学习过程是一个具体的行为过程，其主体是学生。教师应将学习目标拆解成能够让学生经历、体验的有效学习任务，为学生的理解与生生之间经验的互动创造宝贵的机会。如这节课中，王老师没有讲“和平方”的知识点，也没有要求学生一定要掌握“和平方”的结论，而是设置了“请思考如何用学具表示2×（2+3）”“（2+3）2和22+32是否相同？请用学具操作、画图说明或算式解释等方法表达你的想法”“请画图表示（2+4）2，并用等式表示（2+4）2=？”这一系列层次递进的、可操作的体验式任务，让学生在完成任务的过程去发现、比较、建构、迁移、应用，在不断创生修正中，有效积淀学习体验。在这种过程性学习中浸润成长的学生，会形成无论面对何种问题都要寻根问底的深度思考习惯。学生一旦形成稳定而独特的学习特征，就标志着学科核心素养已初步形成。

（二）顺学而教，尊重真实学习自然发生

法国思想家、教育家卢梭倡导教育要回归自然。顺其自然教数学，将人的天性与教育相融合，把内在的“自然”发展要求融入教育实践中，注重启发引导，鼓励学生积极参与学习活动，主动建构和完善知识结构。[2]课堂上王老师尊重学生的真实起点，顺学而教，他创设的每一个任务都从学生的真实发展区切入，鼓励学生大胆尝试；以轻松、自然的交流方式深入，让学生在极具安全感的课堂教学环境中畅所欲言，不断修正。要使学生像数学家那样去思考，就要给予学生自我探索、提出猜想、做出假设、检验结论、进行反驳、调整策略、设计方案、归纳总结、论证结论的机会。创建这样的学习环境，将会促进学生数学创造力的发展。[3]

（三）提供支持，让独立学习成为可能

学生的学习不是凭空可以达成的，教师要为学生搭建合适的脚手架，提供合适的帮助与支持，让学生的独立学习成为可能。本节课上，王老师为学生提供的学具都是有效的支持工具，帮助学生实现了思维的“可视化”，让学生对算式意义的理解主动而深入。王老师借助学具的直观拼搭，将“式”与“形”进行联结，从2×（2+3）的数形联结到（2+3）2和22+32式、形的比较与辨析，每一次王老师都不急于呈现答案，而采用先拼搭、体验、交流，再验证的方式加以创生修正，深度挖掘数学本质，依托可视化的直观呈现，化抽象为具体，变无形为有形。通过几何直观，帮助学生建立画面感，让学生充分感知形与数、形与式，进而建构模式、应用模式，进行识别、创造，助力学生更深刻地理解数学知识。

作为一线数学教师，我们在这节课中看到了真实的学习发生过程。我们在教学过程中都应当“忌急”“忌表”，寓积极于无为，以无为成就有为，尊重教育规律，积淀深度学习体验，寻求深刻、真实的数学学习。