用运动的眼光认识平行四边形

□郝宇雁 郜舒竹

长期以来，小学数学“图形与几何”领域的教学“重算轻看”，重视公式的推理、计算和程序化的操作，而轻视对图形的观察和图形间关系的整体感知。在认识基本图形的教学上更是“轻看”，以“认识平行四边形”为例，不少教师仅通过呈现平行四边形的图片、学生猜想平行四边形的特征、学生验证平行四边形这样的程序来强化学生对平行四边形的认识。[1]这样的教学，看似创设了宽松、和谐的氛围，发展了学生的自主探究能力，实则只是程序性地强化了学生对已有知识的记忆，而缺少视觉感知（Visual Perception）和视觉推理（Visual Reasoning）活动。显然，这种“重算轻看”的教学是亟须变革的。在此，借“用运动的眼光认识平行四边形”来说明“运动”的眼光对学生认识几何图形的重要性。

一、“运动”（Motion）

《现代汉语词典》（第7 版）中对“运动”一词的解释是“物体的位置不断变化的现象。通常指一个物体和其他物体之间相对位置的变化”。《牛津英语词典》中将“运动”看作是某物移动的行为、过程或方式。而哲学范畴中的“运动”是指物质的存在形式及其根本属性[2]，它包括宇宙间所发生的一切变化和过程，从简单的位置运动到人类思维。[3]

关于“运动”，美国认知语言学教授伦纳德·泰尔米（Leonard Talmy）在20 世纪80 年代最早提出“虚拟运动”（Fictive Motion）[4]一词，其最大的特点就是用动态的表达即运动动词来描述静态的场景。虚拟运动是一种心理模拟。[5]在这种情况下，输入大脑中的概念本没有运动，但这些概念被整合成了虚拟运动的场景。[6]比如在“长城从北京一直蜿蜒到嘉峪关”这句话中，长城本是静态的，但经过大脑的整合让我们对长城的位置以及它和其他省市的空间关系有了基本的了解，这就是使用“运动”来呈现静态的场景。可见，“运动”的内涵是如此广泛和深刻：不仅包括实体的移动，而且涵盖了虚拟的运动，甚至囊括了人类思维的发展。

运动变成几何中的基本概念要追溯到菲利克斯·克莱因（Felix Klein，1849—1925）在埃尔朗根大学（University of Erlangen）的演讲[7]，他改变了人们用静止的观点研究几何的传统，将运动的眼光发展到了几何领域（Geometry），他提出运动应该成为人们研究不同空间之间关系的一种思维方式。小学数学中涉及“运动”的主要是“图形与几何”领域中的“图形的运动”，可以理解为几何图形位置发生变化的行为、过程或方式。在变化的过程中，图形的形状和大小始终保持不变，且平面或空间中的所有点保持一对一相关。小学数学教材中，“图形的运动”包括的内容有平移（Translation）、旋转（Rotation）、轴对称（Symmetry/Reflection）。平移即图形中的所有点在平面上沿同一方向移动同样的距离；旋转即一个图形绕给定的点旋转给定的角度；轴对称即一条线像镜子一样反射一个图形。“图形的运动”不仅是一种实体的运动，而且是一种虚拟运动。如果关注运动的过程，图形的位置每时每刻都在发生变化，这便是实体的运动；如果关注运动后的状态，借运动来呈现静止的状态，这就可以理解为虚拟运动。因此，“运动”不仅是一种行动方式，更应当成为一种眼光，帮助儿童认识基本几何图形。

二、运动眼光下的平行四边形

平行四边形（Parallelogram），用“平行”一词来限定“四边形”，使“平行四边形”成为一类特殊的四边形。[8]以静止的眼光看，一个平行四边形是由四条直线段围成的四边形，并且两组对边分别平行且相等，两组对角分别相等。以运动的眼光看，一个平行四边形可以由平移、旋转、轴对称等不同的运动方式得到。下面介绍几种以运动的眼光认识平行四边形的方法。

（一）线段的平移

以运动的眼光来看，图1 中的平行四边形ABCD可以看作是一条运动的线段EF从AB位置平移到CD位置留下的轨迹。平移的方向不是沿着垂直于线段EF的方向，而是沿着与线段EF形成一定角度的方向（图1中线段AD或者线段BC的方向）。在平移的过程中，运动着的“线”留下的轨迹是“面”，概括来说就是“线动成面”。[9]

图1 线段平移形成平行四边形示意图

（二）三角形绕一边的中点旋转

如图2 将三角形ABC绕BC边的中点O顺时针旋转180°，旋转后得到的三角形和原三角形共同组成平行四边形AC′A′B′。原B点经旋转变成B′点且与原C点重合，原C点经旋转变成C′点且与原B点重合，原A点经旋转变成A′点。

图2 三角形绕一边中点旋转形成平行四边形示意图

由此可见，将任意一个三角形绕其一边的中点进行旋转可以得到相应的平行四边形，这个过程也可以看作是由两个完全一样的三角形拼成了一个平行四边形。在小学数学课堂上，教师教学《三角形的面积》时常说的一句话就是“两个完全一样的三角形可以拼成一个平行四边形”。这是借助了转化的数学思想，将未知的三角形转化为已知的平行四边形，进而推导其面积的计算方法。

（三）三角形两边取中点后绕点旋转

以运动的眼光看，平行四边形还可以看作是将三角形两边取中点后绕点旋转而得到的。[10]如图3，在三角形ABC的AC边和BC边上分别取中点D和E，并连接DE（此时DE边平行于三角形的底边AB且长度为AB边的一半），便得到了小三角形CDE。将小三角形CDE绕E点顺时针旋转180°后，原C点变成C′点且与原B点重合，原D点变成D′点。由旋转得到的三角形C′D′E与原梯形ABED共同组成平行四边形AC′D′D。同理，也可以将小三角形CDE绕D点逆时针旋转180°后（原C点变成C′点且与原A点重合，原E点变成E′点）和原梯形ABED共同组成平行四边形BC′E′E（如图4）。

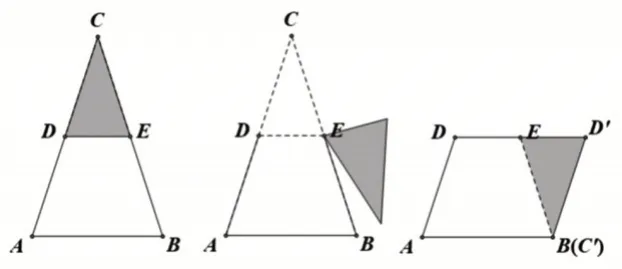
图3 三角形两边取中点后绕E 点顺时针旋转形成平行四边形示意图

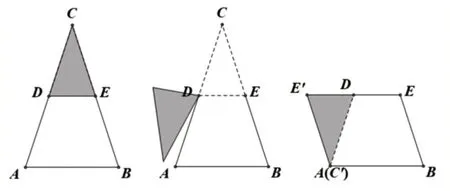
图4 三角形两边取中点后绕D 点逆时针旋转形成平行四边形示意图

（四）直角三角形的轴对称变换

如图5，直角三角形ABC经过两次轴对称变换可得到平行四边形AB′A′B。具体操作如下：将直角三角形ABC以短直角边BC所在的直线为对称轴进行第一次轴对称变换，原A点经轴对称后得到A′点，原三角形ABC经轴对称变换后得到三角形AA′B（其中点A、C、A′经轴对称变换后在一条直线上）。在此基础上，将三角形AA′B以AA′边所在的直线为对称轴进行第二次轴对称变换，之后形成平行四边形AB′A′B。

图5 直角三角形经两次轴对称变换后形成平行四边形示意图

（五）凸四边形中的平行四边形

如图6，有凸四边形ABCD，在其四条边AB、BC、CD、DA上分别取中点E、F、G、H，顺次连接EF、FG、GH、HE四边（此时边EH、FG均平行于BD边，且长度为BD边的一半；边EF、HG均平行于AC边，且长度为AC边的一半），可得到平行四边形EFGH。这是在凸四边形中绘制平行四边形的第一种方法。

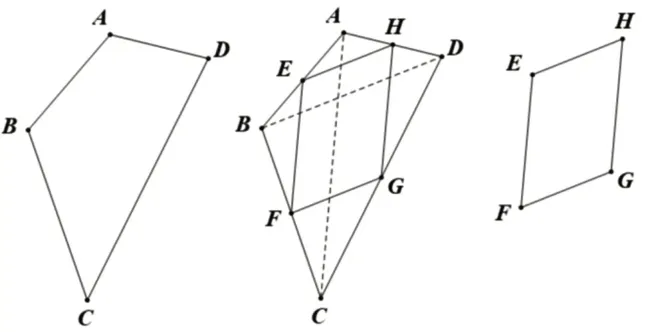
图6 凸四边形中绘制平行四边形示意图

除此之外，还可以借助旋转、平移等变换将凸四边形ABCD转化成平行四边形EFF′E′。具体操作如图7 所示：在上述操作的基础上，将三角形AEH绕H点顺时针旋转180°得到三角形A′E′H（原A点经旋转变成A′点且与原D点重合，原E点经旋转变成E′点）；将三角形CFG绕G点顺时针旋转180°得到三角形C′F′G（原C点经旋转变成C′点且与原D点重合，原F点经旋转变成F′点）；将三角形EBF沿线段BD的方向平移线段BD的长度得到三角形E′B′F′（原E点经平移变成E′点，原F点经平移变成F′点，原B点经平移变成B′点且与原D点重合）；变换后的三个三角形和原三角形HDG组成平行四边形HGF′E′，并因此得到新的平行四边形EFF′E′。这是将凸四边形分割后的各部分进行平移和旋转的运动而得到平行四边形的第二种方法。

图7 凸四边形形成平行四边形示意图

除以上方法外，还可以将不同的图形进行不同的运动而得到平行四边形。运动的眼光是一个全新的视角，用运动的眼光重新审视生活中司空见惯的图形，这是一种突破，也是一种提升，有助于整体感知图形间的关系，发展初步的空间能力。

三、运动的眼光对小学数学的教学价值

将数学的核心素养落实在小学数学教学中，要求学生会用数学的眼睛看，会用数学的思维想，会用数学的语言说。[11]运动的经验是普遍的，它渗透到人类生活的各个方面，与运动相关的语言可以渗透到语言表达中没有真实运动的领域。[12]以运动的眼光观察物体正是培养了学生用数学的眼睛看世界的能力，学生能够从图形与图形的关系中抽象出概念与概念的关系，把握概念的关键特征。认识基本图形的教学正是要让学生掌握概念的关键特征[13]，通过图形的运动体会不同图形、不同概念之间的关系，进而把握每一种图形的关键特征。

以运动的眼光认识基本图形为学生观察物体提供了新的视角，并且发展了学生初步的空间观念。点动成线（如流星划过夜空留下的轨迹）、线动成面（如汽车的雨刷在摆动时形成的图形）、面动成体（如以长方形纸片的一边为轴旋转后得到的圆柱体）背后都蕴藏着常见的生活现象。教师应该引导学生用运动的眼光审视日常生活，加深对数学知识的理解，提升学生的空间观念，空间观念的提升能为初中乃至以后的学习奠定基础。

不仅如此，以运动的眼光认识基本图形还能培养学生的数学审美能力和创新意识。在以运动的眼光审视世界的过程中，学生发现图形运动形成的图案之美，发现图形运动和艺术与生活的联系，进而培养学生感受美、鉴赏美、创造美的能力。早在20 世纪初，荷兰图形艺术家莫里茨·科内利斯·埃舍尔（Maurits Cornelis Escher，1898—1972）就受数学的启发进行艺术创作，他借助图形的运动创作了许多精美绝伦的作品。[14]在埃舍尔“对平面的规则划分”的创作方式中大量使用了平移、旋转、轴对称等变换，这也让他的作品极具数学的图形之美。同样如此，学生也可以在掌握图形运动的关键特征的基础上进行艺术创作，这充分体现了马克思主义关于人的全面发展学说的相关内容，实现智育和美育的和谐统一。

数学教学的培养目标之一就是要让学生会用数学的眼睛看，培养学生的数学眼光。“运动”作为数学眼光的一种，它不是一种现象，而是一种方法，一种工具，一种思维，一种模拟现实世界的模型，它是我们学习数学、认识世界的重要抓手，对人的视觉感知能力和视觉推理能力的发展起到巨大作用；它理应受到重视并被广泛应用。