循证学习：回归数学“真学习”的教学探索

□王 江 陈睿萱

真实的学习过程隐匿在儿童的脑海中，而儿童的大脑对于教师而言，无疑是一个暗箱，教学活动的推进，常常成为教师基于主观经验的一种选择。如何让学生的思维“被看见”？应倡导基于“证据”的学习，即“循证”学习。

一、意义叩问：“循证”的概念与价值探寻

（一）何为“循证”：对“循证”学习的概念界定

循证，即遵循“证据”，基于循证的教学不再通过经验、臆测来“推进”，而通过“循证据”来展开，如：可以根据课标要求展开课前调研、进行学生访谈、反馈作业数据等来获取学生的真实信息，尽可能地暴露学生的思维痕迹，教师在此基础上，准确把握学生存在的学习障碍，制订更为优化的教学决策。

（二）为何“循证”：对“循证”学习的价值追溯

1.内隐思维显性化

基于“证据”的数学学习，强调通过说一说、写一写、画一画等方式暴露思维痕迹，触摸学生不可见的内隐思维，与学生的“真实思维”相遇。

2.教学决策更优化

教师习惯于根据教师用书的规定、自己的教学经验等展开教学，学生的真实想法常常被掩盖。而基于“证据”的学习，教师可以清晰地看到不同层次学生真实的思维痕迹，有助于根据学生的认知难点和困惑设计出以学习者为中心的教学策略。

3.深度学习真发生

基于“证据”的学习，通常有以下4个环节：①收集证据：不依赖“主观经验”，收集学生已有“证据”；②准确分析：证据背后潜在的问题，到底是什么；③有效引导：改变这样的状况，需要对学生进行哪些引导；④优化反思：怎样的教学行为才能实现有效的学习引导。

二、实践诠释：如何基于“证据”，回归数学“真学习”

（一）收集“证据”，研读学生的“前经验”

收集“证据”，是为了充分暴露学生已有的真实起点，了解学生在探索问题过程中可能出现的多元方法，同时深入挖掘学生之间的“差异”。

1.设计大问题：给学生需要的探究空间

大问题是指针对一节课或一个环节的核心发问，它通常直指问题的本质，具有一定的探究空间，每一个学生都可以在探索中呈现自己对问题的真实理解。如教学苏教版教材五年级上册《解决问题的策略》一课时，教师设计了这样一个大问题：

工人叔叔打算用22根l米长的木条，围一个面积为20平方米的长方形花圃。如果这些木条要全部用完，而且不能折断，你觉得他能完成这个任务吗？把你的思考过程记录下来。

通过解答大问题，不同层次的学生都获得了思维留痕的机会，部分典型作品如图1所示。教师可以清晰地看到每一个学生的“前经验”。教师要做的就是在学生的真实起点上，引导学生完成对新知识的主动建构，实现思维的进阶。

图1

2.提供小工具：让“差异”成为课堂资源

教师在收集“证据”的过程中，应当充分考虑学生的差异，创设各种机会，提供可操作的小工具，促进不同层次学生的发展。

（1）提供小锦囊

在估算《读者》杂志一页纸字数的活动中，教师提出如下要求（如图2）。

图2

对于思维水平高的学生，教师要求他们自主探究，对于思维水平一般的学生，教师给出了“算、画、折、撕”的提示，而对于思维薄弱的学生，教师则提供了小锦囊。这样让每一个学生都参与到活动中来，获得学习的成功体验。

当然，小锦囊并不是直接给出答案，而是通过之前的学习素材来呈现，唤醒学生的某种经验。如这一活动中教师提供的小锦囊如图3所示，它还原了当时探索的主要步骤，旨在唤醒学生的经验，将其迁移到新情境中。

图3

（2）开展小打卡

小打卡，是每个学生获得学习体验、留下思维痕迹的好工具，针对自觉性不够、对教师布置的研究任务采取敷衍态度的学生，很有效果。

如教师在苏教版教材二年级下册《分米和毫米》一课的教学中，提供了这样一张学习单（如图4）。

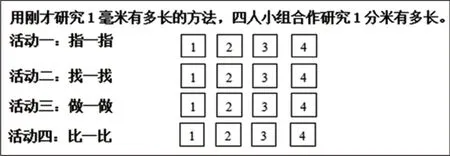
图4

师：这四个活动按照顺序一个一个进行。以“指一指”为例，你看后面有四个学号，哪一个组员已经指出来了，就在对应的学号上打钩。四位同学都完成了活动一，才能进行活动二。

实践过程有序、高效，组内各个层次的学生还可以互学互教，能够充分地学习到其他学生的观点，真正把每一个学生都全程卷入活动之中。

（二）分享“证据”，看见每一种思维

教师要努力让各种层次水平的学生，都有分享的机会。

1.多元对话，让交流有层次感

可以按从“小组互学”到“全班展学”、从“低层次”到“高层次”这样两个原则展开。

（1）从“小组互学”到“全班展学”

小组互学时，每个成员都进行了有序分享、倾听、对话、提问等学习过程，其他成员或补充、或质疑，组内已悄然完成了一次思维的进阶。教师应当在课堂上重现这样的思维进阶历程，以启发更多的学生。

如在解决以下问题时，有的学生直接写“12、10、8、6”（如图5），组内成员立刻提出了质疑：“如果1 枚1 枚调整，比如11，11 枚5 角的话，肯定会出现□.5 元，不是整元。”在随后的全班展学中，教师追问：“通过小组内的交流，哪些同学有了新的收获？”“12后，怎么一下子就思考11？”顺势请这个小组与全班学生分享。这样的思维进阶历程重现，使得学生获得了一次对数感的真体验。

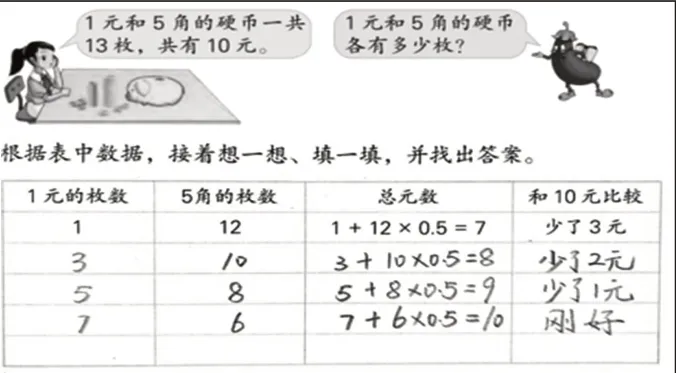
图5

（2）从“低层次”到“高层次”

证据分享时，建议先分享思维层次较低的，再逐渐过渡到思维层次高的，从不规范到规范、不全面到全面，符合儿童认知规律。逐步递进的分享，也能够保证不同层次、不同风格的思维痕迹都被看见，学生的学习历程也更加清晰、完整。

如从前文中《解决问题的策略》（苏教版教材五年级上册）学生运用的四种方法，容易看出：作品①，学生的思考是无序的；作品②，学生抓住“周长不变”展开有序列举，不重复也不遗漏；作品③，学生的思考角度不同，抓住“面积不变”展开有序列举；作品④，学生已经清楚知道“差小积大”的规律，且灵活运用。

学生的思考过程究竟是怎样的？教师也可以通过追问去寻找丰富的证据。比如对于作品④，教师可以追问：“‘差小积大’，究竟是什么意思？”这样，就显现了学生静态思维成果背后的动态思考过程。

2.减少干预，让对话过程变长

如果剖析学生互动的情形，通常就是质疑、评价等6种方式（如图6）。教师若把其运用在自己的课堂中，便可丰富生生对话的过程。

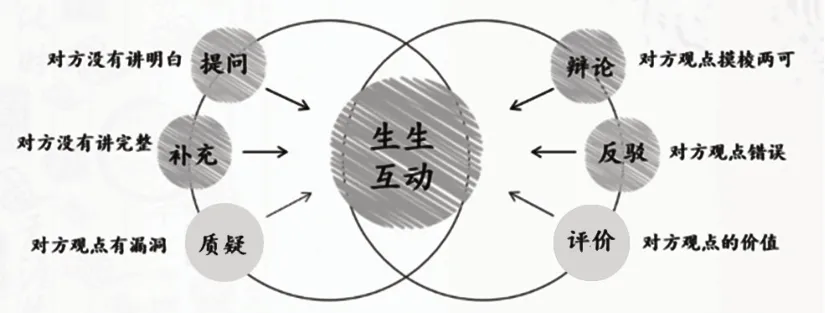
图6

●提问：对方没有讲明白，教师可引导学生提问：“你刚才提到的某某观点是什么意思，我们没有听明白，你能再讲一遍吗？”

●评价：待对方讲完后，教师可以引导学生进行评价：“你画了图/举例子/做实验，我们听得特别明白！”

……

教师有意识地在课堂上多实践，学生自然会长时间“占住”讲台，生生之间的对话在这个过程中被拉长，教师这个“权威”适度隐退，在一旁捕捉更多的证据，以调整和优化后续的教学进程。

（三）关联“证据”，实现思维的进阶

证据从收集到分享，学生思维有进阶，但通常还停留在模糊、零散、肤浅的阶段，这就需要教师关注不同“证据”之间的关联度，使学生的认知走向清晰、结构与深刻。

1.巧“织网”：经历知识的完整建构

学生获得的知识，如果没有完满的结构把它联在一起，那是一种多半会被遗忘的知识。如在苏教版教材六年级上册《解决问题的策略》新授课结束后，笔者增加了如下环节。

师：假设，其实一直存在于我们的学习过程之中。图7 中，哪里用到了假设？有什么好处？

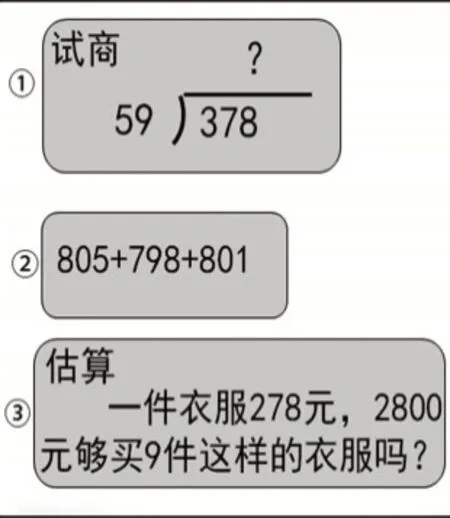
图7

生：第①题，59 假设成60，然后60 乘6 等于360，很靠近360了，很可能商6，我觉得可以很快帮助我们找到商。第②题，每一个数都可以假设成800，然后再加5，减2，加1，假设可以帮助我们更简便地进行计算。第③题，假设买10 件，278 乘10 那就是2780元，所以是够的。

师：看来，同学们已经对假设这一策略有了很深的认识。这里还有一张图（苏教版教材四年级下册《解决问题的策略》主题图），找到假设了吗？

生：假设小春和小宁同样多，那么总数就是72-12=60枚……

师：看来，假设一直存在于我们的学习过程之中。同学们，这一次的假设，和我们刚才学习的假设，有何不同？（略）

结构化的知识对能力的形成有相当的促进作用。这样的知识具有严密的逻辑性、丰富的关联度，教师要对教材有深刻的理解，要善于实现不同证据的关联，如将书本上呈“碎片化”的知识加以重构，使知识呈现出整体的“结构态”。

2.善“播种”：体会知识技能和思想方法的完整关照

证据的关联可以是多样的，如：对与错的关联；同中求异、异中求同的关联；简单与复杂的关联；现在与未来的关联……关联的最终目的，就是为了引领学生“登高”，实现思维进阶。如在《平行四边形的面积》新授课结束后，教师这样引导：部分同学想到用相邻的两条边相乘，现在知道这种算法是不对的。但老师很想跟大家分享，这个想法没有全错，只不过在相邻两条边相乘时，还要考虑第三个因素，也就是再乘上一个系数就对了。在中学数学里是用一个计算公式表达的：S=absinθ……

正确方法和错误方法的对比，实际上就是一次证据的“关联”，学生能够在这样的“证据关联”中感悟正确的面积计算方法，之后教师又把错误的方法和未来在中学要学的知识进行关联，悄悄地播下一颗种子，让学习变得完整、动态、鲜活，有利于学生的长程发展。

3.常“反思”：凸显思维进阶感悟的完整过程

无论是成功的学习经历，还是失败的学习体验，都有反思的价值。课堂上教师可以引导学生说一说自己的“原证据”以及与“现证据”对比后的感悟，用思维进阶的历程启发更多的学生。如：今天我学会了什么？我是如何学会的？我曾经有哪些困惑？我是怎么解决这个困惑的？

（四）补充“证据”，提升学生的学习能力

“证据”的补充，可以让学生的持续性发展成为可能。教师可以引导学生补充“好题推荐”“我来提醒”“我有困惑”等证据，也可以提供“数学读物”以及指向素养提升的挑战题，让不同层次学生的学习能力得到进一步提升。当然，这对教师的数学素养提出了极大挑战，如：哪些好题指向本节课的核心知识？这些好题呈现的顺序是怎样的？

总之，基于“证据”的数学学习，可以让隐性的思维显性化，让看不见的学习活动被“看见”，让教学决策成为一种基于可视化证据的科学判断，从而让深度学习真正发生！