抗压制干扰的离散相位编码序列设计

杜 盈，王志诚，张劲东，蒋宜林，尹明月

（1.南京航空航天大学 电子信息工程学院，江苏 南京 211100；2.上海无线电设备研究所，上海 201109）

0 引言

压制干扰就是干扰机发射大功率噪声或类似噪声的干扰信号来遮盖或者淹没目标信号，使雷达无法检测到目标，干扰雷达的正常工作。对抗压制干扰，包括陷波滤波器、自适应滤波器、子空间投影等方法，这些方法是利用干扰信号与真实目标回波之间的强度特征差异来滤除干扰，但陷波滤波器方法受到滤波器零陷宽度的限制，自适应滤波器法和子空间投影法在时变干扰环境下也不够稳健。

从波形设计的角度研究对抗压制干扰的方法，要求干扰信号经过滤波器的输出水平尽可能低。干扰信号经过失配滤波器的输出水平可用滤波器序列和干扰信号协方差矩阵的二次型表示，该二次型值越小说明雷达的抗干扰能力越强。文献［13］考虑最小化接收滤波器输出功率；文献［14］以发射信号距离旁瓣和干扰信号输出水平之和构建代价函数；文献［15］以最大化信干噪比为准则，联合优化发射波形和失配滤波器序列来达到对抗干扰的目的。如果只优化发射波形1 个变量，可采用匹配滤波器，此时，干扰信号通过匹配滤波器的输出水平用发射信号与干扰信号协方差矩阵的二次型值来表示。文献［16］以最大化信干噪比为准则设计单位模序列，可有效抑制主瓣干扰，但未考虑使用匹配滤波器带来的高距离旁瓣问题。

本文以最小化发射信号距离旁瓣为准则，预设的干扰输出水平和离散形式相位编码为约束条件，设计离散相位编码序列。该问题的目标函数是关于发射信号的四次型，本文采用交替乘子法（Alternating Direction Method of Multipliers，ADMM）嵌套拟牛顿法，即用ADMM-BFGS 方法进行求解，可将干扰信号输出抑制在预设值，同时降低发射信号旁瓣；在此基础上，提出一种ADMM 嵌套类幂迭代法（Power Method-Like Iterations，PMLI），即ADMM-PMLI 方法，在保证雷达的抗干扰性能和目标探测性能的同时，大大提升算法的计算时间。

1 问题模型

雷达发射波形为离散相位编码序列，1 个点的相位编码信号序列可表示为

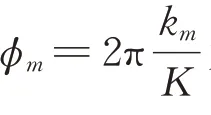
发射信号旁瓣协方差矩阵为

式中：为转移矩阵，定义为

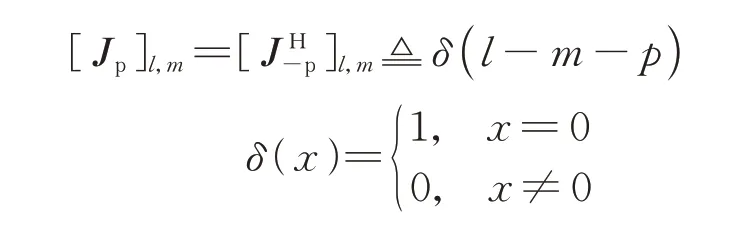
发射信号距离旁瓣为

设干扰信号协方差矩阵为，∈C，干扰信号经匹配滤波器的输出为

设置干扰经匹配滤波器的输出水平为，抗压制干扰的离散相位编码序列设计问题可表示为

2 求解目标函数

2.1 ADMM-BFGS

在该问题中引入辅助变量、，约束=，=，问题可表示为

设、为二次惩罚项系数，根据问题写出增广拉格朗日方程如下：

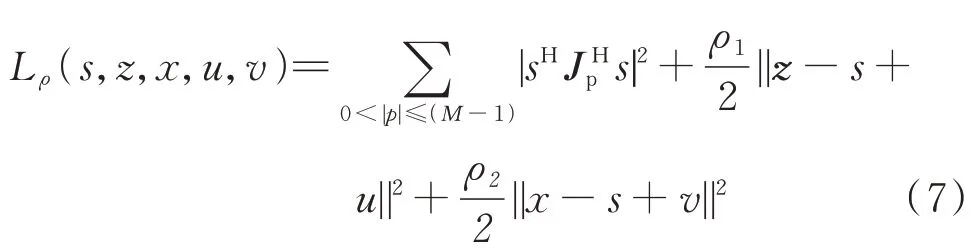
记、、、和为 第次迭代后的值，各值的更新如下。

1）更新。

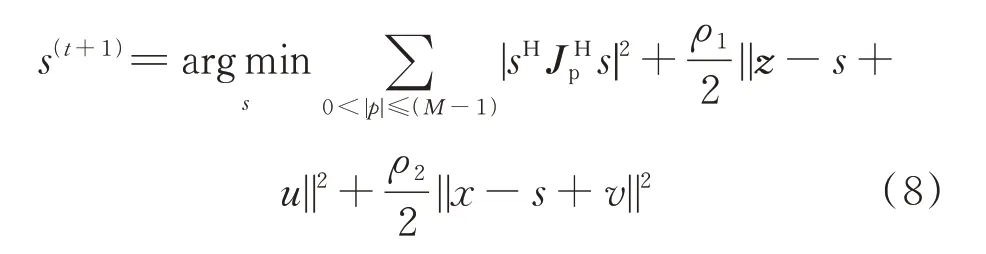
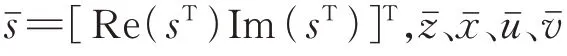
将目标函数式（8）由复数形式转化为实数形式：

对目标函数式求得梯度如下：

2）更新。

此时将和视为已知量

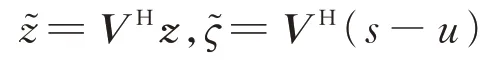
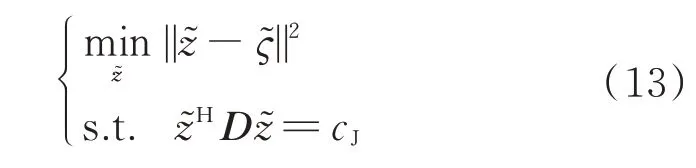
式（13）相关的拉格朗日函数为

式中：为拉格朗日乘子，令其偏导为0，可得

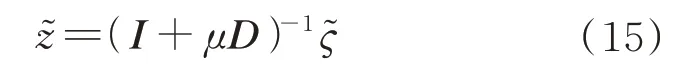
将式（15）代入等式约束可得

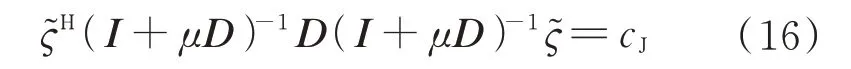
该式可等价于

解出后可得的更新公式如下：

3）更新。

4）更新。

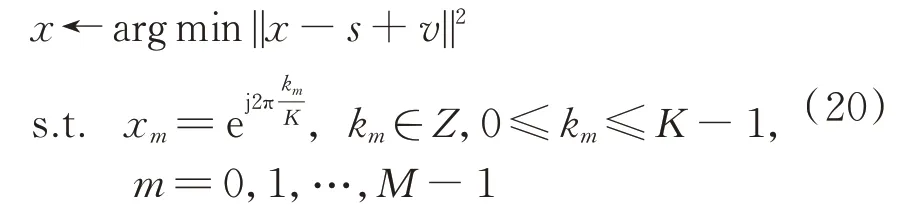
求得的更新公式为

5）更新。

ADMM 求解问题步骤如下：

初始化、、、和，预设干扰输出水平，设迭代次数=0；

根据式（19）更新；

根据式（21）更新；

根据式（22）更新；

设收敛门限为Δ，最大迭代次数为，重复步骤2～步骤6，并令←+1，直到满足||||+||-||＜Δ 或=时，迭代终止。

2.2 ADMM-PMLI

采用ADMM-BFGS 算法更新时，需要转化数据形式并计算梯度，其运算量大、计算时间长。针对这一问题，本节将在ADMM 方法的基础上进行优化，提出ADMM-PMLI算法来更新。式（8）可改写为

令()+))，()+))，忽略常数部分，式（23）可表示为

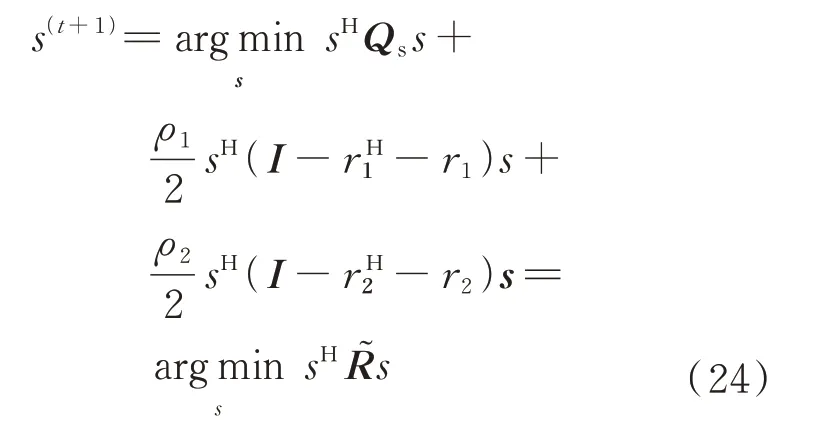
根据文献［17］提出的PMLI 算法，发射信号的更新即求解表示为

发射信号可以通过每次迭代求解最近向量问题更新如下：

ADMM-PMLI 求解步骤如下：

初始化、、、和，预设干扰输出水平，设迭代次数=0；

更新，根据式（27）求解；

以式（18）更新；

根据式（19）更新；

根据式（21）更新；

根据式（22）更新；

设收敛门限为Δ，最大迭代次数为，重复步骤2～步骤6，并令←+1，直到满足||||+||-||＜Δ 或=时迭代终止。

2.3 算法复杂度分析

ADMM-BFGS 和ADMM-PMLI 算法均以ADMM 为框架，两种算法的主要差别在于变量的更新。ADMM 每次迭代更新时，BFGS 法的复杂度为（4），而PMLI 法的复杂度为（）。且相较于ADMM-PMLI，ADMM-BFGS 还需进行变量实数和虚数形式的转化，这一操作增加的运算复杂度为（2）。如果算法运行到+1 次时，迭代终止，那么上述部分还需乘以迭代次数。因此，ADMMPMLI 算法的复杂度明显低于ADMM-BFGS。

3 仿真结果与分析

发射信号自相关处理结果可以显示发射信号的旁瓣水平，反映雷达的探测性能。将发射信号与干扰信号叠加后经过匹配滤波器处理，观察目标能否被检测到，以反映雷达对抗压制干扰的能力。为验证本文提出的ADMM-BFGS 和ADMM-PMLI这两种算法是否有效，将两种算法优化后的自相关与匹配滤波结果和初始发射信号进行对比，结果如图1 所示。

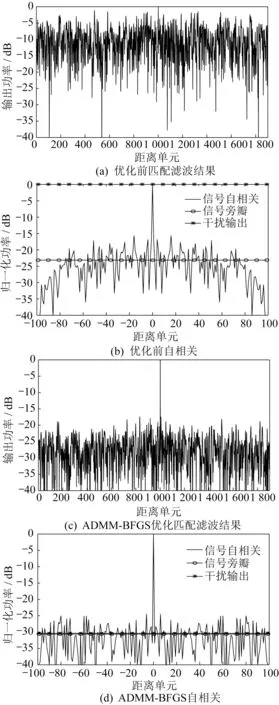
图1 优化前后信号处理结果对比Fig.1 Comparison of signal processing results before and after optimization

续图1 优化前后信号处理结果对比Continue fig.1 Comparison of signal processing results before and after optimization

对比图1（a）和（b），在发射信号未受到干扰时，经过匹配滤波后可以看到明显的尖峰，能检测到目标，而发射信号叠加干扰后经匹配滤波处理，检测不到目标信号，目标信号被强干扰淹没。由图1 所示的被优化前后的匹配滤波结果可知，优化前无法检测到目标信号，优化后压制干扰被抑制，可以检测到信号。综上所述，ADMM-BFGS 和ADMMPMLI 这两种算法均能对抗压制干扰。通过对比优化前后发射信号的自相关数据，优化后的信号旁瓣比优化前有明显降低，且干扰输出均能被抑制在-30 dB 左右，达到了预期效果。

ADMM-BFGS和ADMM-PMLI这两种算法的收敛曲线图如图2 所示，横坐标为迭代次数，纵坐标为发射信号旁瓣功率。由图2 可知，两种算法的目标函数值随着迭代次数不断降低，两种算法均能收敛。

图2 算法收敛曲线Fig.2 Algorithm convergence curve

为对比算法性能，本文在Intel i5-9400HQ CPU、16 GB 内存、Matlab 2016a 仿真平台下进行了100 次蒙特卡洛实验取平均值，获得两种算法优化后的发射信号距离旁瓣减少值Δ、干扰输出功率和运行时间在信号序列长度不同时的结果，见表1。

表1 ADMM-BFGS 和ADMM-PMLI 算法性能对比Tab.1 Performance comparison of ADMM-BFGS and ADMM-PMLI algorithms

由表1 可知，离散相位编码序列长度越长，算法对信号距离旁瓣的抑制效果越明显。两种算法均能降低信号旁瓣，且达到预期的干扰输出水平，其抗干扰性能和目标探测性能基本相当，但是，相较于ADMM-BFGS 算法，ADMM-PMLI 算法的运行效率得到大幅提升。

4 结束语

本文设计离散相位编码序列来对抗压制干扰，以最小化发射信号距离旁瓣作为目标函数，预设的干扰输出水平和离散相位作为约束条件，构建优化问题模型，采用ADMM-BFGS 算法优化发射信号序列，提升雷达的目标探测性能和抗干扰能力；同时，针对ADMM-BFGS 算法运算量大、计算时间长的问题，提出一种新的ADMM-PMLI 算法。仿真结果表明，这两种算法具有相当的目标检测性能和抗干扰能力。但是，相较于ADMM-BFGS 算法，ADMM-PMLI 算法的运行效率得到大幅提升。