机器人组装超大型结构的姿-轨-柔耦合动力学仿真

王启生，蒋建平，李庆军，江国期，周铃松

（中山大学航空航天学院，广东广州 563100）

0 引言

随着航天科技的发展，世界各国都认识到空间组装技术对未来航天器设计与建造模式的重要性，纷纷对空间组装进行了大量的工程实践、方案论证和学术研究。超大型航天器的结构尺寸达到数百米甚至数千米，包括空间太阳能电站、超大口径卫星天线、人工重力场航天器等。受限于现有运载工具的运送能力，这些构造复杂、尺寸巨大的空间结构往往无法通过地面装配、整体发射的方式升空。空间组装技术成为建造超大型航天器的关键技术。

建立空间组装过程的动力学模型，研究组装过程航天器姿态与结构的动力学特性，是实现超大型航天器空间组装的基础。史纪鑫等针对大型复杂航天器组装过程小变形情况，采用模态综合法建立了非线性动力学模型，并通过动力学仿真验证了其有效性。WANG 等研究了太阳能卫星在轨装配过程中的分布式自适应振动控制，并通过控制单元和整个SPS结构之间的关系建立了控制单元的动态模型。荣吉利等采用自然坐标法与绝对节点坐标法对空间太阳能电站的刚性与柔性构件建立了动力学模型，研究了组装时间、组装机构的阻尼和刚度系数对组装过程的影响。然而，上述研究聚焦于组装过程的结构动力学问题，未涉及空间机器人的组装控制。

利用空间机器人协助或替代宇航员在太空中执行超大型航天结构空间组装、空间站的建造等操作，一方面可以确保良好的操作精确度，提高自主性和灵巧性；另一方面能够克服在轨应用的经济与技术障碍。文献［6-7］推导了具有柔性附件的空间机器人系统的刚柔耦合动力学模型，基于动态耦合模型设计了闭环控制系统，空间机械臂在抑制结构振动的同时成功捕获运动目标。CHEN等将柔性附件和刚性飞行器主体组成的柔性航天器合理地简化为自由浮动的毂梁系统，针对组装过程中航天器之间的碰撞以及挠性部件的振动问题，提出了一种复合控制方法。时月天等基于仿生理论，设计了一种适用于空间太阳能电站空间组装的足型机器人，安装过程中空间机器人可在薄膜和桁架之间自由爬行。张瀚博等针对复杂条件下空间桁架组装具有局限性的问题，创新设计了一种适用于空间桁架空间组装的空间机器人，提高了组装效率。程靖等针对漂浮基空间双臂机器人在轨服务时易于航天器发生碰撞的问题，建立了空间机器人捕捉大型航天器动力学方程，并研究了捕捉过程镇定运动最优控制方法。朱安等设计了一种旋转型串联弹性执行器，有效避免了空间机器人捕捉卫星过程中关节之间相互碰撞冲击。然而，上述研究并未考虑万有引力梯度和姿-轨-柔耦合效应的影响。

机器人空间组装超大型结构的动力学与控制涉及机器人多体系统动力学建模与轨迹规划、大柔性结构刚柔耦合建模、航天器轨道和姿态动力学、自动控制，以及万有引力及其梯度等空间环境多个学科领域，给精确动力学建模、耦合动力学分析、控制系统设计带来极大困难。CAO 等针对OMEGA 空间太阳能电站圆形反射镜支撑结构的组装问题，通过传统“车-桥耦合”模型研究了组装过程的结构动力学响应。然而，上述研究并没有考虑机器人的操控过程，也没有考虑组装过程的姿-轨-柔耦合效应。

综上所述，超大型空间结构由于超大的尺寸和超低的固有频率，在复杂空间环境和机器人操控干扰下会产生结构振动、姿态摆动、轨道漂移等复杂动力学行为，对机器人控制精度、控制执行机构、组装精度等造成影响。然而，当前研究或是没有考虑机器人对大柔性结构的控制，或是没有考虑复杂空间环境和姿-轨-柔耦合效应，无法完全模拟机器人空间组装超大型结构的过程。本文考虑万有引力梯度力矩、结构的几何非线性，建立组装过程中主结构-空间机器人-待组装结构的姿-轨-柔耦合动力学模型，通过机器人的轨迹规划和轨迹跟踪控制，实现超大型结构的组装过程动力学仿真。与现有文献不同的是，本文的动力学仿真能同时给出组装过程的轨道动力学响应、姿态动力学响应、结构振动响应、机器人控制力矩与关节误差、笛卡尔空间的组装误差等丰富的动力学响应，为组装过程研究提供有价值的参考。

1 动力学建模

本章以主结构-空间机器人-待组装结构组成的系统为研究对象，建立姿-轨-柔耦合的动力学方程。组装系统如图1 所示，其中1～7 为机械臂连杆，为机械臂关节点，点与点为机械臂末端抓取点。主结构和待组装结构是空间太阳能电站的支撑桁架结构，在此简化为欧拉-伯努利梁。由于结构尺寸较大，在组装过程中可能出现较大的变形，所以采用绝对节点坐标法描述。相比而言，空间机器人的尺寸较小、刚度较大，因此将其简化为多刚体系统，采用自然坐标法描述。组装系统的质量和几何参数见表1～表2。

图1 空间组装系统Fig.1 Space assembly system

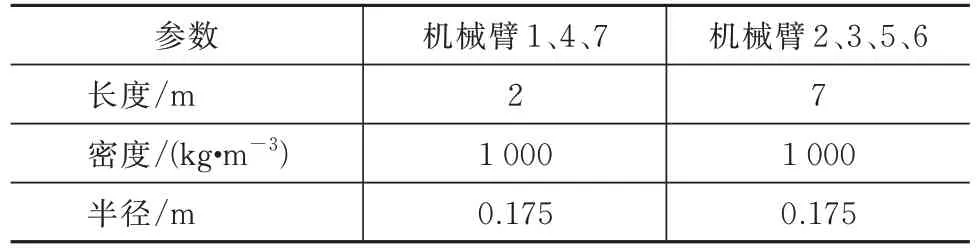
表1 空间机器人的参数Tab.1 Parameters of the space robot

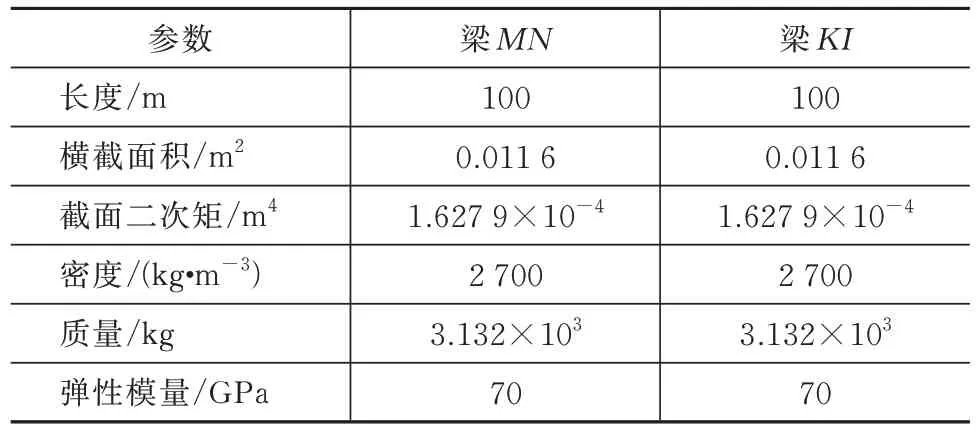
表2 结构参数Tab.2 Parameters of the structures

为了研究组装过程中主要的动力学特性，在本文中作以下几点假设：1）只研究系统在轨道平面的运动，从而大幅降低模型复杂度，节省动力学仿真时间；2）仅考虑万有引力和引力梯度，忽略其他空间摄动力/力矩的影响；3）假设空间机器人已经实现了对主结构和待组装结构的抓捕，只研究主结构和待组装结构在空间机器人控制作用下相互靠近的过程，忽略关节柔性、摩擦等非线性因素。

空间机器人由7 个刚体构成，采用自然坐标法进行刚体的动力学建模。平面刚体的自然坐标法采用刚体上2 个点的位置矢量和固连于刚体上的单位矢量来描述刚体。本文选取的空间机器人广义坐标为

式中：v为刚体上与轴线垂直的单位矢量，如图2所示。

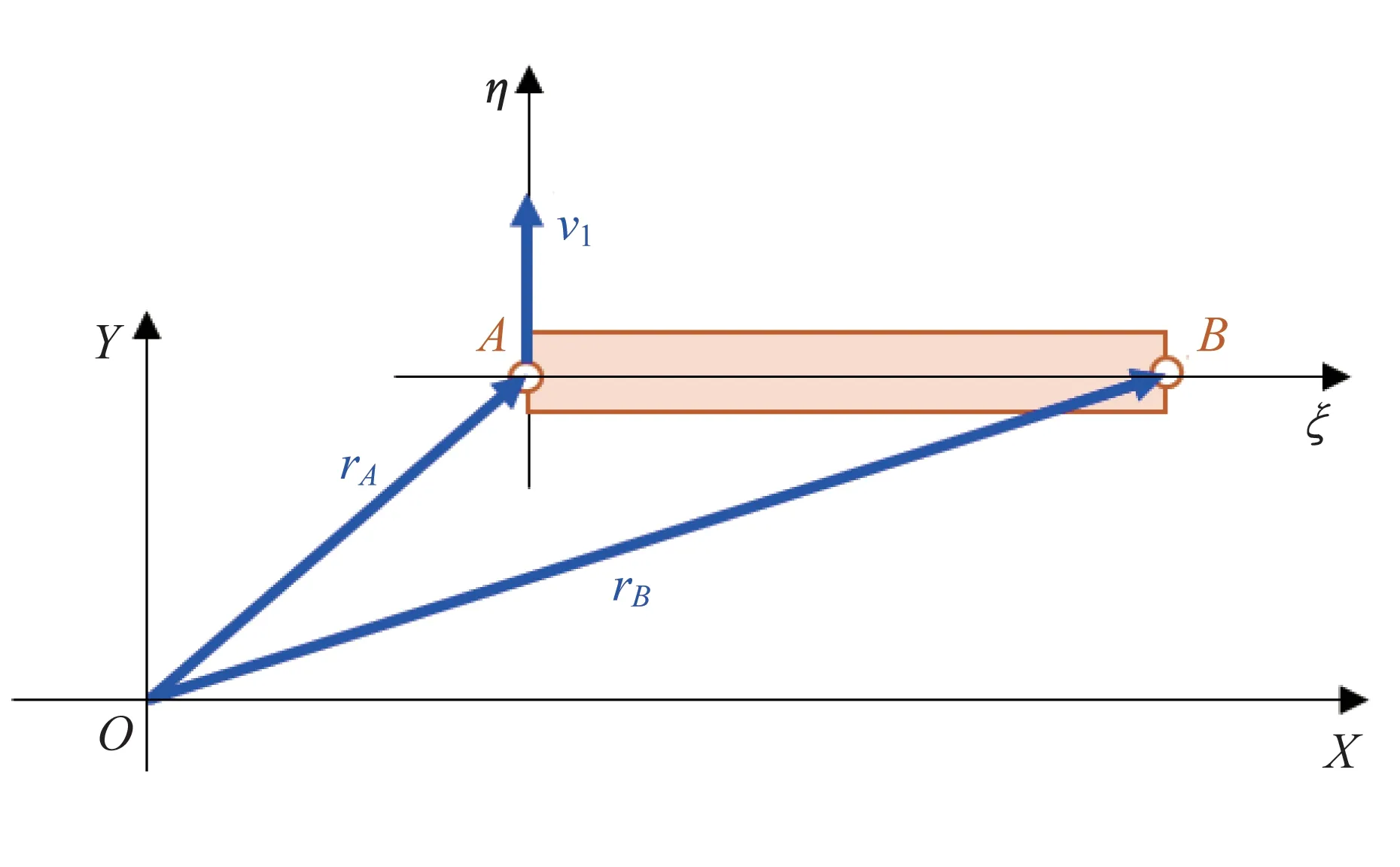
图2 刚体AB 的自然坐标描述Fig.2 Natural coordinates of the rigid body AB

由于空间机器人只有9 个自由度，式（1）拥有30个广义坐标，因此有21 个约束：

式中：r和r为刚体的左端点和右端点的位置矢量，例 如和分别 为r和r；为各 刚体的 长度。

式（2）也可以缩写为

主结构和待组装结构均采用绝对节点坐标法进行建模，采用一维二节点欧拉-伯努利梁单元进行离散。这种绝对节点坐标法单元具有2 个节点，每个节点具有4 个广义坐标，因此单元具有8个广义坐标：

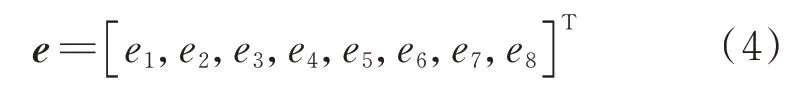
广义坐标中的元素具体定义为

式中：为单元内的局部坐标；为单元的长度。

对于主结构-空间机器人-待组装结构组成的系统，广义坐标为

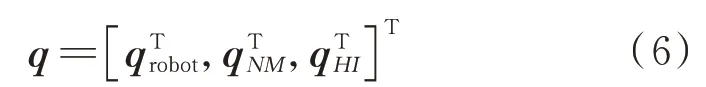
式 中：q∈R和q∈R分别为主结构和待组装结构的广义坐标；n和n分别为和的单元数。

根据约束Hamilton 变分原理，系统的动力学方程为

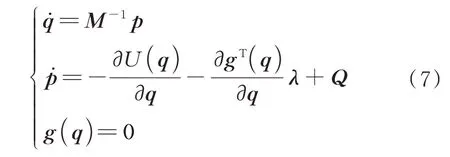
式中：为质量矩阵；为广义动量；为势能；为广义外力向量；为Lagrange 乘子。

系统的又可以表示为

式中：、、分别为机器人、主结构和待组装结构的万有引力势能；和分别为主结构和待组装结构的弹性势能。

系统的质量矩阵可由机器人、主结构和待组装结构的质量矩阵组装而成。由于自然坐标法和绝对节点坐标法在现有文献［18］中已有较多研究，本文主要给出自然坐标法和绝对节点坐标法的万有引力及其梯度表达式。

基于微元法的思想，刚体或柔性体单元上任意一个质量元（位置矢量为）的万有引力势能为

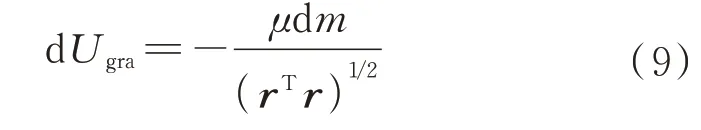
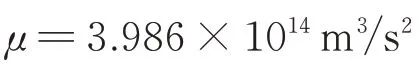
因此，刚体或柔性体的万有引力势能可通过体积积分表示为

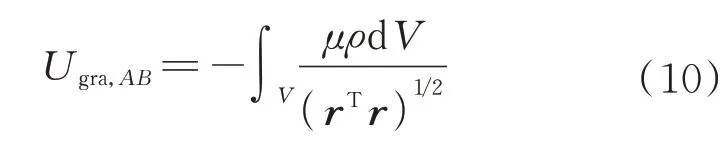
式（10）中的被积函数是非线性函数，无法直接获得体积积分的解析表达式。为此，将被积函数在刚体或单元的质心处作二阶Taylor 级数展开，得

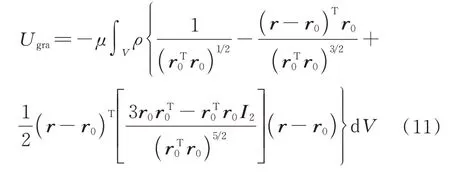
整理得

式中：被积函数为位置矢量的二次函数，可分为3部分分别积分。第1 部分的被积函数是常数，体积积分是刚体或单元质量的表达式；第2 部分的被积函数是的线性函数，体积积分是刚体或单元质心的表达式；第3 部分是的二次型，体积积分可得到惯性矩阵的表达式。

由于式（12）保留了Taylor 展开的2 阶项，所以最终的动力学方程中不仅包含刚体或柔性体单元的万有引力，还包含万有引力梯度。

为了描述空间机器人与主结构/待组装结构之间的抓捕关系，本文将位置重合、相互垂直的抓捕关系等效为直线与扭转的线性弹簧-阻尼系统，弹性系数取为10，阻尼系数取为10。

2 组装过程的轨迹规划

本章给出空间机器人的轨迹规划和轨迹跟踪控制方法，使主结构和待组装结构相互靠近，直至对接。为了描述空间机器人的轨迹，建立局部坐标系，轴指向初始时刻点，姿态角为，如图3 所示。组装过程中坐标系的保持不变，而不总是指向点。～、～为关节角度，为从轴到直线的角度。

图3 空间机器人关节角度Fig.3 Joint angle of the space robot

对点在坐标系的轨迹进行规划。点始终在轴上沿轴负方向运动，且和始终垂直于轴。为满足初末时刻的相对速度和加速度要求，采用五次多项式对点的坐标进行如下规划：

本文考虑初末时刻的相对速度和相对加速度均为0 的情形，则初末时刻的条件为

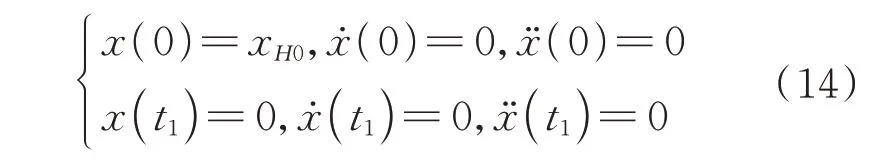
式中：为组装末时刻。

将式（13）代入式（14）得

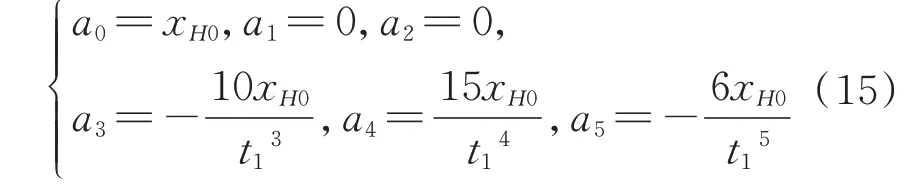
通过上述轨迹规划已经得到点的轨迹，根据几何关系可得到机械臂系统关节角度～的轨迹规划曲线。

几何关系包括3 方面：1）空间机器人在组装过程中始终保持对称构型；2）点的坐标x由式（13）计算；3）空间机器人的质心的坐标在组装过程中保持不变（本文选为=6 m）。

于是有

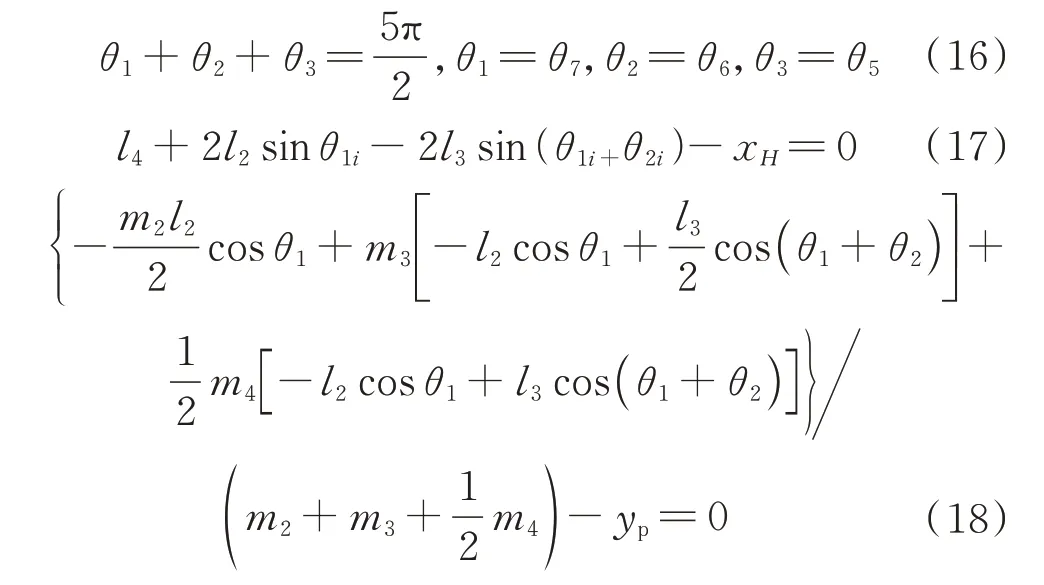
式中：、、为机械臂2、3、4 的长度。

得到关节空间的轨迹后，采用PD 控制方法对轨迹进行跟踪控制。

在本文的数值仿真中，假设安装阶段的时间为=300 s，给定x=18 m、=6 m，从而得到安装阶段的轨迹规划结果，如图4 所示（始终为0，、、分别与、、重合）。

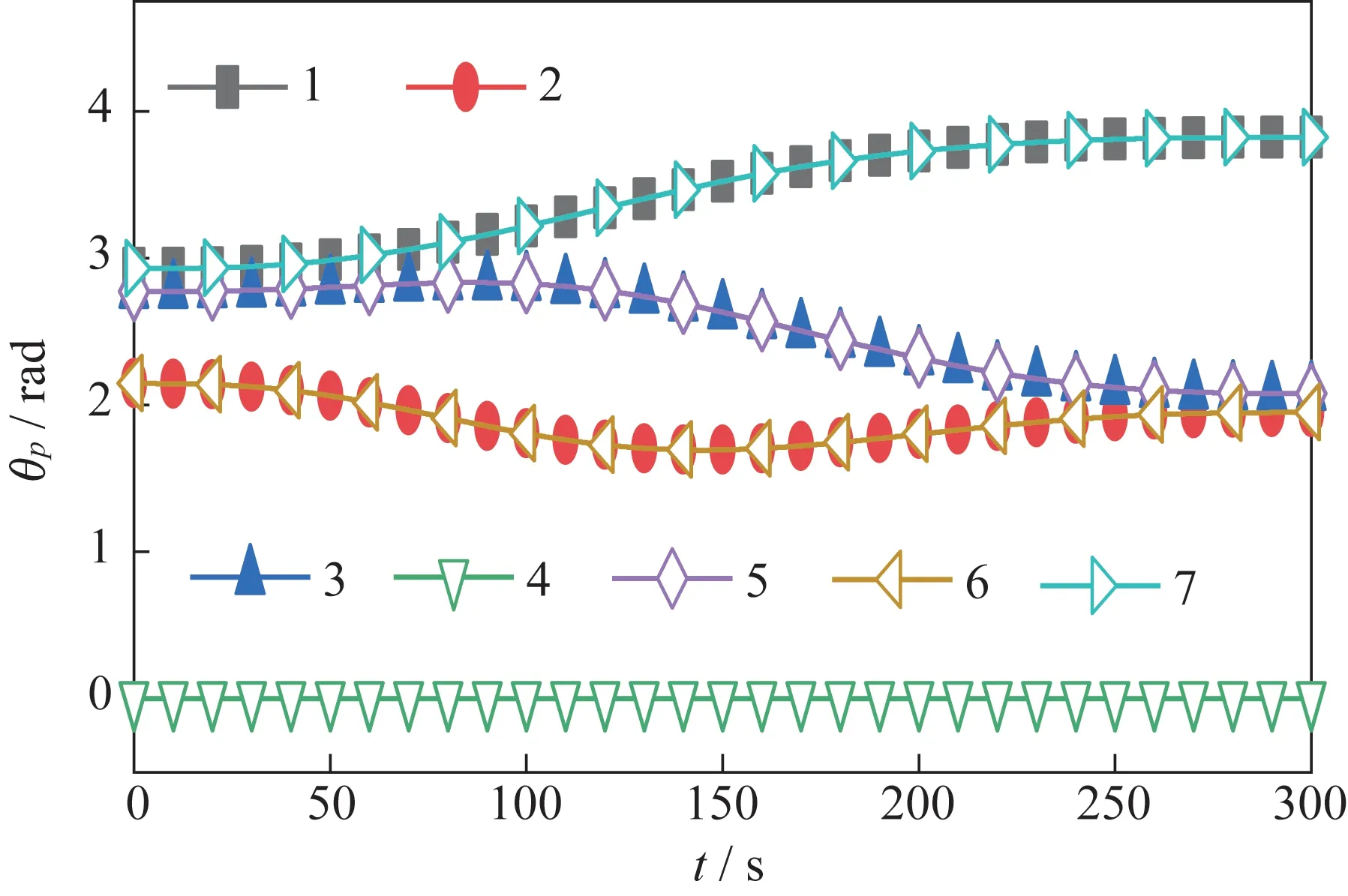
图4 空间机器人关节角度变化Fig.4 Variations of the joint angles θp（p=1，2，3，4，5，6，7）of the space robot

3 仿真分析

本章对空间组装过程进行动力学仿真。为研究万有引力与引力梯度对组装过程的影响，数值仿真分为4 种情形，见表3。

表3 数值仿真的三种情形Tab.3 Three cases for the numerical simulations

情形2 和情形3 系统初始位于半径为7 137 km的圆形轨道，轨道周期为6 000 s，组装系统的初始姿态角分别为0°和45°。情形2 和情形3 考虑了万有引力的影响，因此考虑了轨道-姿态-结构耦合效应。由于情形2 的姿态角为0°，所以基本上不受万有引力梯度力矩的影响。作为对比，情形1 不考虑万有引力、万有引力梯度与轨道-姿态-结构耦合效应的影响，是现有文献普遍采用的方式。3 种情形主结构与待组装模块初始未变形，仿真分析时间步长为0.001 s。

如图5～图6 所示，情形2 和情形3 由于没有考虑轨道摄动的影响，系统的轨道离心率和长半轴的变化量非常小，符合轨道动力学特性，验证了动力学仿真的有效性。由于情形1 没有考虑轨道与姿态，所以不存在离心率与半长轴。

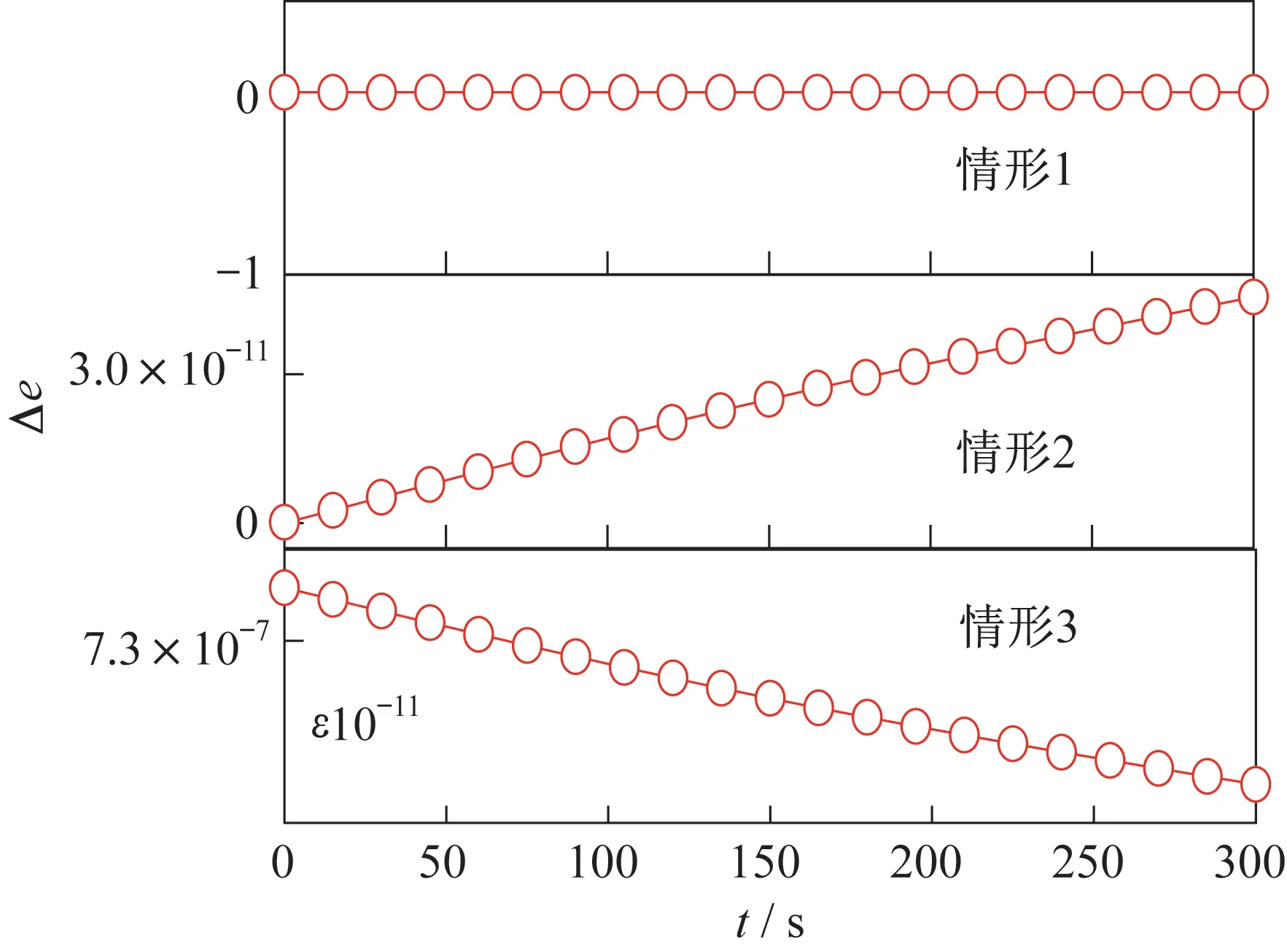
图5 离心率变化Fig.5 Variations of the eccentricity e

图6 长半轴变化Fig.6 Variations of the semi-major axis a

主结构和待组装结构的姿态角变化曲线如图7所示。由图可知，情形1 的组装过程由于没有考虑万有引力与引力梯度的影响，主结构与待组装结构姿态角变化极小，最大值仅为(1.24×10)°。虽然情形2 选择了稳定的姿态角0°进行组装，但由于组装过程整个组装系统在绕地球转动，因此组装过程结构受柯氏力的影响，在姿态控制系统作用下仍然出现了(5.18×10)°的小幅姿态运动。情形3 的初始姿态角为45°，在万有引力梯度和科氏力的共同影响下，姿态角出现了明显的变化，达到了0.01°，对组装精度造成显著影响。

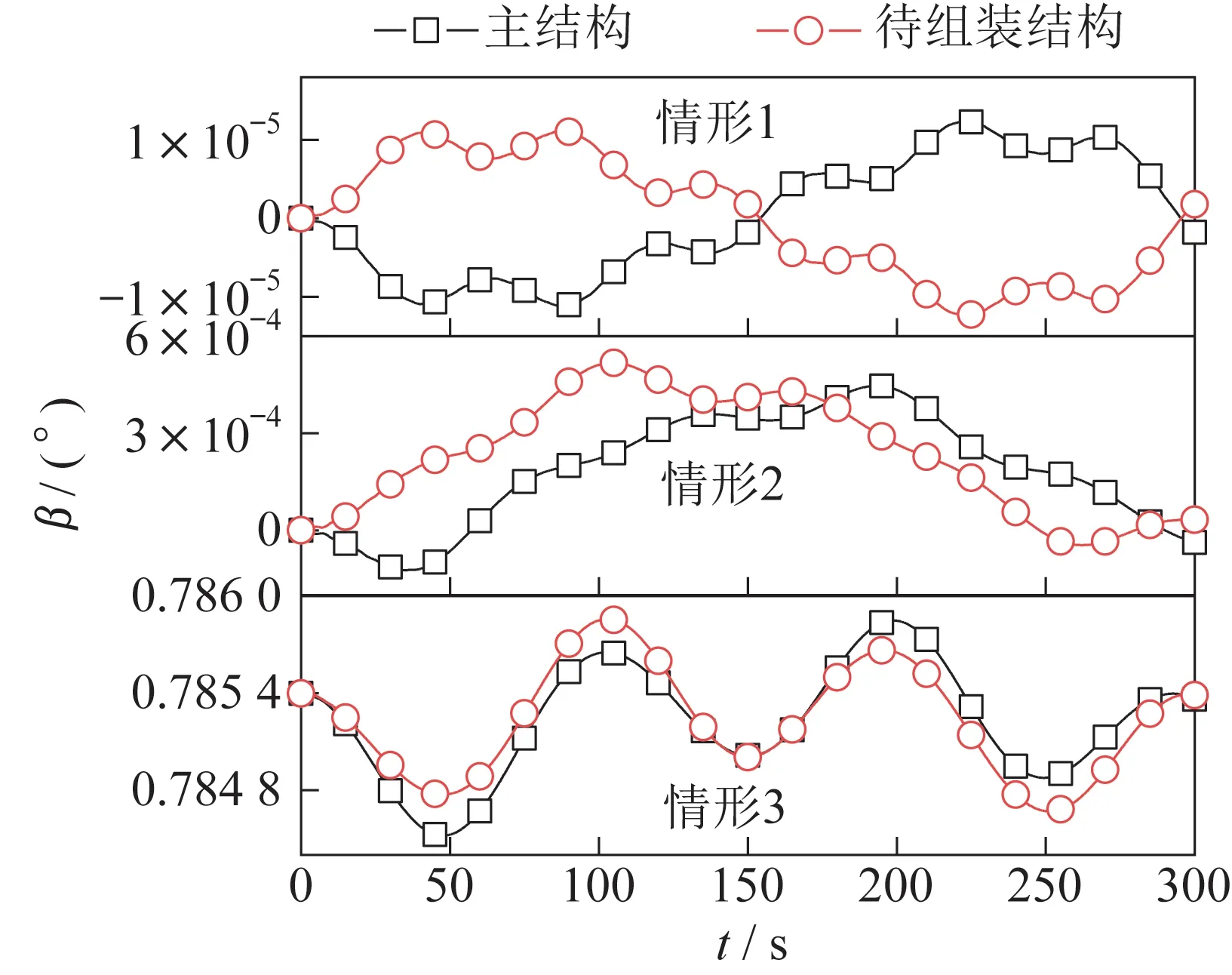
图7 姿态角变化Fig.7 Variations of the attitude angle β

空间机器人关节角度误差曲线和控制力矩曲线如图8～图9 所示。由图可知，情形1 到情形3 的关节角度误差依次增加，情形1 的关节角度误差最大为(6.31×10)°，情形2 为(1.02×10)°，情形3为(1.21×10)°。在考虑万有引力梯度与轨道-姿态-结构耦合效应以后，情形2 和情形3 的关节角度误差不再像情形1 那样呈现对称变化。在控制力矩方面，由于不受万有引力梯度和科氏力的影响，情形1 的空间机器人控制力矩最大值为29.0 N·m，且始终为0。在考虑万有引力梯度与科氏力的影响后，情形2 的最大控制力矩为47.6 N·m，情形3 的最大控制力矩为57.7 N·m，且在空间组装过程中，不同关节的控制力矩曲线随时间的变化趋势不同。由此可见，万有引力梯度和科氏力对组装过程控制力矩的影响非常大。

图8 空间机器人关节角度误差Fig.8 Joint angle error of the space robot eA

图9 空间机器人控制力矩Fig.9 Control moment of the space robot M

点在坐标系的坐标，如图10～图11 所示。由图可知，组装过程主结构和待组装结构在方向按轨迹规划的五次函数平滑靠近，最终对接时相对速度几乎为0，能较好地避免组装过程的碰撞。对于点的坐标，本文在轨迹规划时要求空间机器人质心在方向保持不变。由图可知，情形1 的y变化量小于4.29×10m。对于情形2 和情形3，由于万有引力梯度和轨道-姿态-结构耦合效应的作用，y的变化量分别为0.001 7 m 和0.004 4 m。由于y基本可以反映组装精度，因此万有引力梯度和轨道-姿态-结构耦合效应对组装精度造成显著影响。

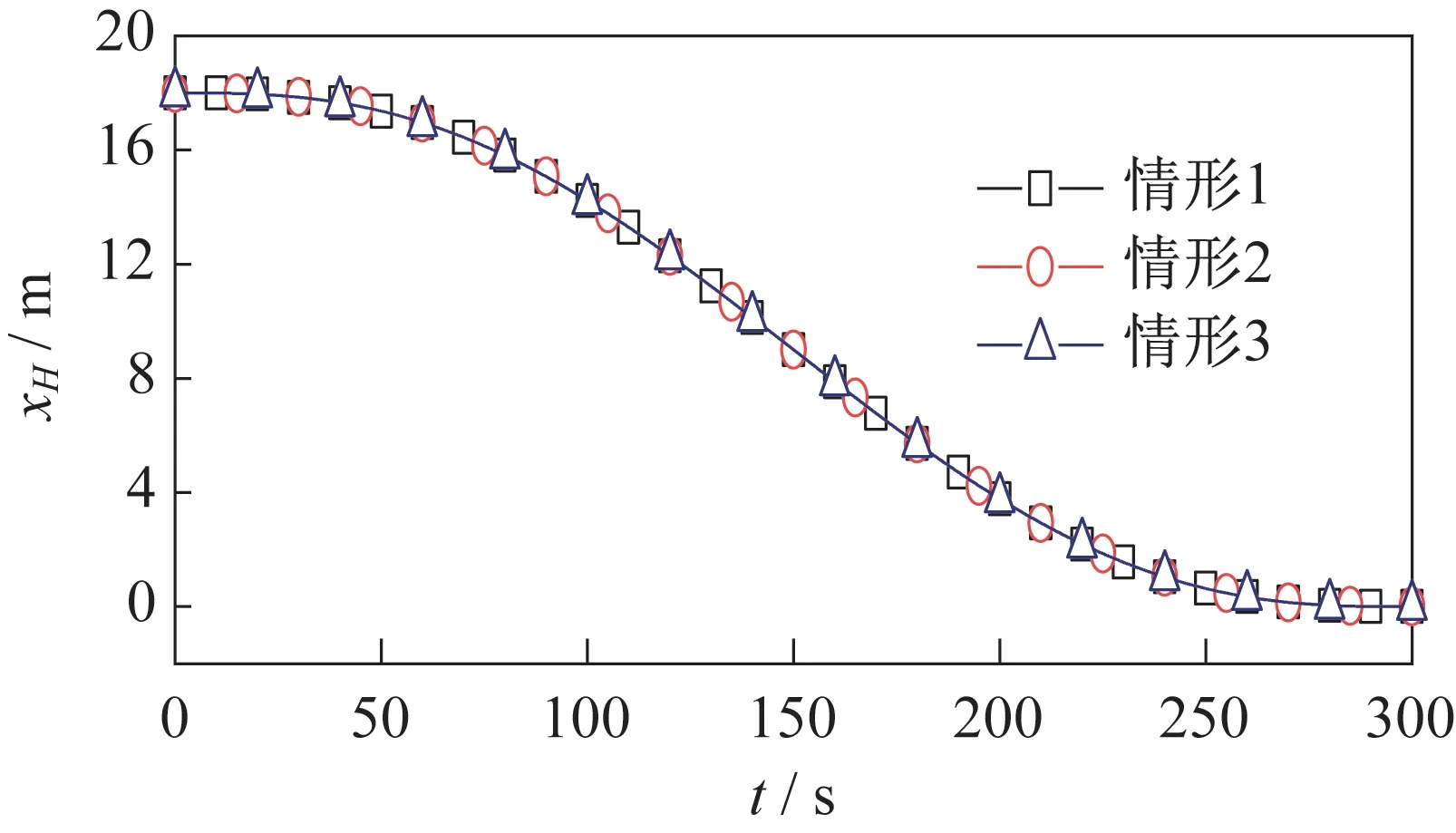
图10 点H 的x 坐标Fig.10 The x coordinates of Point H

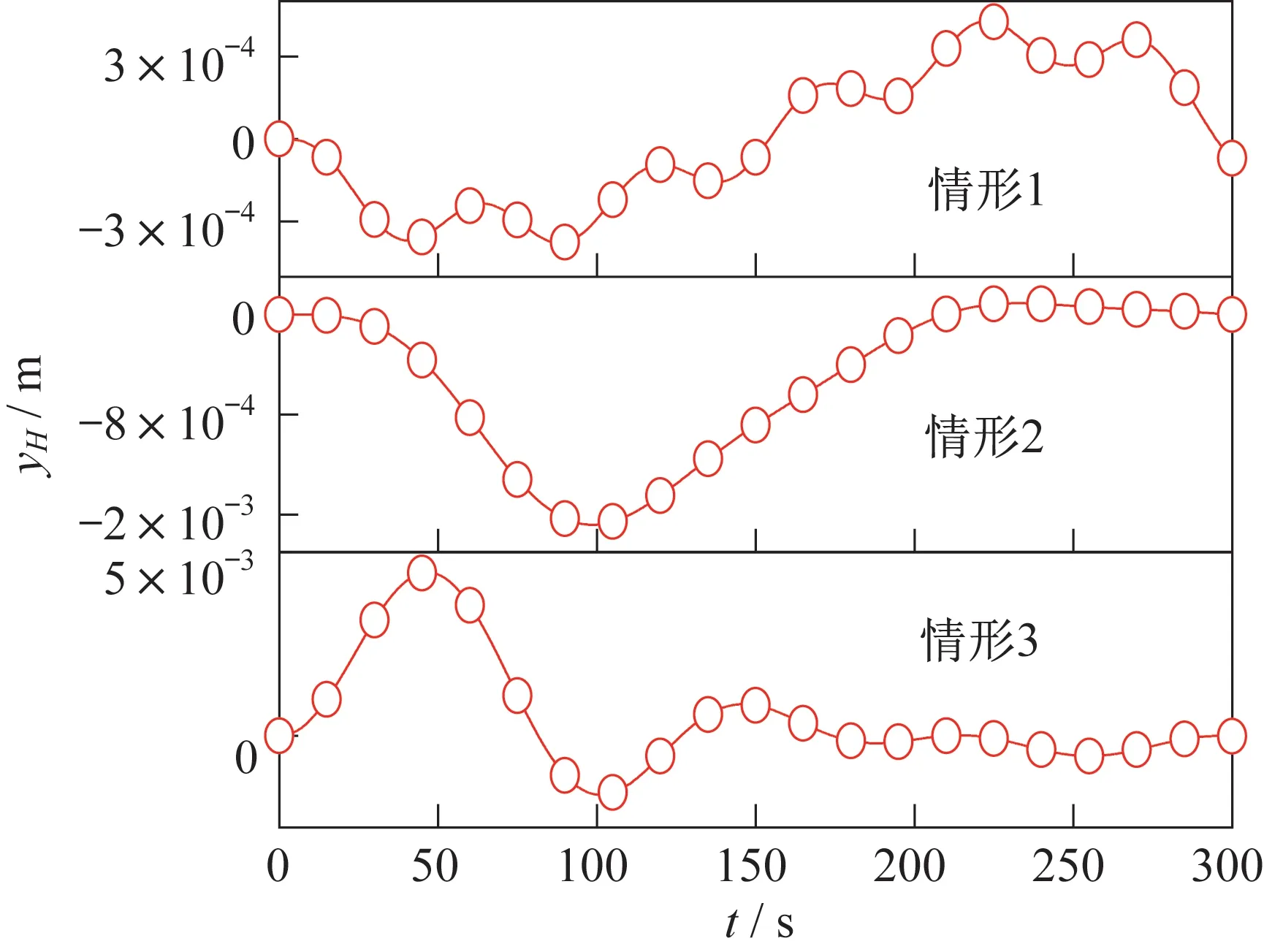
图11 点H 的y坐标Fig.11 The y coordinates of Point H

组装过程主结构和待组装结构的振动如图12所示。由图可知，情形1 组装过程中的最大结构振动幅值仅为6.81×10m。对于情形2，虽然姿态角为0°，万有引力梯度的影响可以忽略，科氏力仍然引起小幅结构振动，最大幅值为0.004 6 m。对于情形3，在万有引力梯度和科氏力的影响下，结构振动为0.008 8 m。

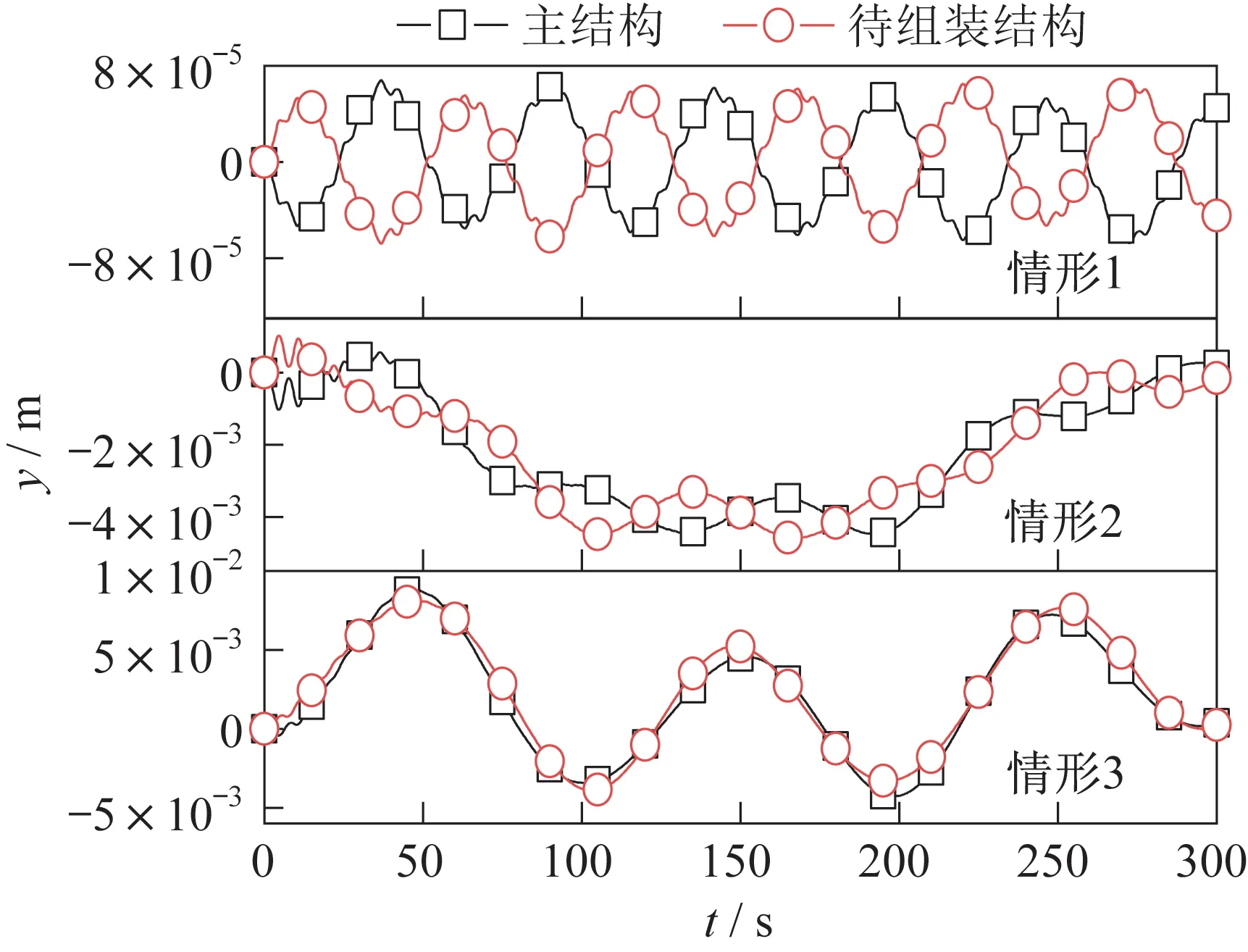
图12 组装模块结构振动Fig.12 Structural vibrations of the assembled modules

4 结束语

本文针对空间机器人组装超大型结构的动力学与控制问题，基于自然坐标法和绝对节点坐标法，建立了主结构-空间机器人-待组装结构复合系统的姿-轨-柔耦合动力学模型，研究了万有引力梯度和姿-轨-柔耦合效应对组装过程的影响。由于系统绕地球进行轨道运动，组装过程会产生科氏力。通过数值仿真发现，对于超大型结构，万有引力梯度和组装过程的科氏力使空间机器人的控制力矩大幅增加，且对组装精度产生显著影响。因此，在超大型结构的组装过程中，必须考虑万有引力梯度等空间摄动和轨道-姿态-结构耦合效应的影响。