高轨卫星远程抵近轨道优化研究

刁华飞，尚晓龙，王 培，芦 雪

（1.航天工程大学，北京 101416；2.中国人民解放军32030 部队，新疆 和硕 841200）

0 引言

近年来，随着高轨卫星数量的日益增加以及太空军事化进程的加速，轨道抵近与邻近操作（Rendezvous and Proximity Operations，RPO）正在变得越来越频繁。RPO 包含轨道抵近和邻近操作两部分。其中，轨道抵近需要通过多次机动变轨，匹配与目标卫星的轨道高度、轨道平面以及在轨相位。高轨卫星处于地球同步轨道（Geosynchronous Earth Orbit，GEO）带的不同相位上，常使用调相机动的方式达到抵近的目的。调相转移用时一般为轨道周期的正整数倍，这使得抵近过程往往需要较长的时间。而对于任意位置、任务时间约束下的轨道拦截，基本采用基于Lambert 转移，当进行远程抵近时消耗燃料过多。因此，轨道抵近过程中的轨迹优化设计在高轨抵近任务中有着重要意义。远程抵近高轨非合作目标时，往往需要大幅调整、快速响应，一般采用化学燃料的脉冲变轨。脉冲变轨的主要问题，就是研究在航天器燃料约束下，从初始轨道至目标轨道的转移过程中，航天器施加脉冲的时机、次数以及脉冲矢量的方向和大小，这是一个非线性最优规划的问题。

对于脉冲轨道转移，国内外学者已经取得了许多成果。非线性交会研究多是基于不考虑摄动的二体运动学方程。当追踪星和目标星均处于圆轨道时，若对转移时间没有约束，则平面内的最优交会是双脉冲的霍曼转移。霍曼转移仅局限于共面圆轨道的情形，而Lambert 转移则可以适用于任何轨道，因此Lambert 转移方法被广泛应用于非线性最优交会研究中。1963 年，LAWDEN基于二体模型给出了脉冲变轨的“主矢量”理论，用于确定脉冲作用下最优转移轨道的必要条件。1968年，LION 等在LAWDEN研究 的基础上，提出一种冲量校正理论，通过增加脉冲次数、初始漂移或减少脉冲次数实现对非最优轨迹的速度增量优化。在上述理论基础上，不少学者对最优脉冲交会进行了深入研究，一些新的优化理论应运而生，如非线性规划法、遗传算法、蚁群算法、模拟退火算法、粒子群算法、差分进化算法（Differential Evolution，DE）等。文献［10］采用非线性规划求解固定时间内两异面椭圆间的燃料最省的多脉冲交会问题，并对三脉冲和四脉冲方式进行轨迹优化计算；文献［11］采用动态规划算法求解多脉冲最优交会问题；文献［12］采用进化算法，以燃料和时间为组合优化指标，对非固定时间的轨道转移和拦截问题进行优化；文献［13］采用非线性规划算法对不同拦截时间和脉冲次数的优化情况进行了比较分析。

针对高轨卫星远程抵近的轨道设计优化问题，本文使用Pork-chop 速度增量等高线图对时间约束内单脉冲Lambert 转移进行分析，而后提出一种收敛性较好的多脉冲抵近优化设计模型，使用DE 对多组算例进行全局寻优。

1 高轨转移动力学建模

1.1 卫星在轨受力分析

对于高轨卫星而言，中心天体的引力显然是最主要的外力源，除此之外还需考虑各种摄动力的影响，由此可建立受摄二体模型如下：

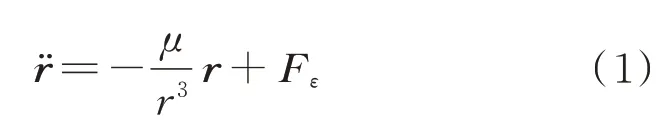
本文的研究对象是高轨卫星，在这个空间范围内，地球大气对卫星产生的阻力可忽略不计，这里主要考虑地球的非球形摄动力太阳。因此，本文研究所使用的轨道外推模型仅考虑含J2 项的地球非球形摄动加速度：

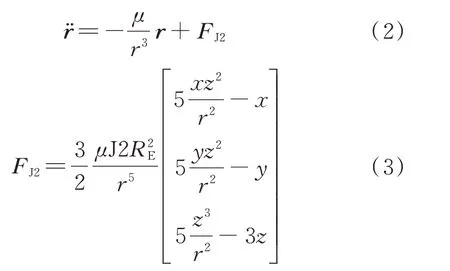
式中：为含J2 项的地球非球形摄动加速度；[]为卫星在地心惯性坐标系下的位置坐标；为地球半径。

1.2 Lambert 转移与求解算法

Lambert 转移描述了2 个圆锥曲线轨道之间的固定点交会，被广泛应用于空间轨道设计领域，适用于研究高轨抵近任务。Lambert 是关于圆轨道上任意2 个时刻的位置坐标同时间的关系定理，给定2 个位置矢量和它们之间的飞行时间，便决定其飞行轨道。Lambert 定理的数学表述为

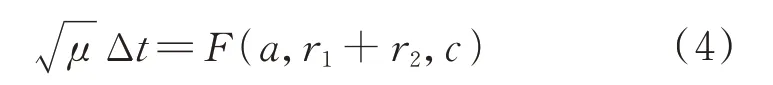
式中：为转移轨道的半长轴；为转移轨道始末点之间的距离；Δ为转移时长。

欧拉和拉格朗日用解析法证明了Lambert 定理，并求得了二体模型下Lambert 问题的解析解：

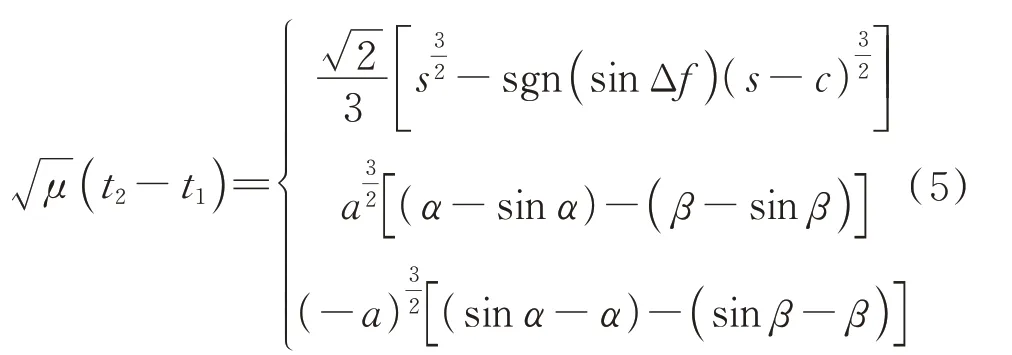
变量和由等式参数(，+，)决定，定义如下：

式中：变量=(++)∕2，表示三角形的周长。

Lambert 转移基 于Lambert 定理提 出，已知2 个位置坐标和转移时间确定飞行轨道，如图1 所示。已知机动卫星初始点位置矢量为，速度矢量，目标星的位置矢量为，速度矢量，转移时间为=-。根据Lambert 定理，可以求解。

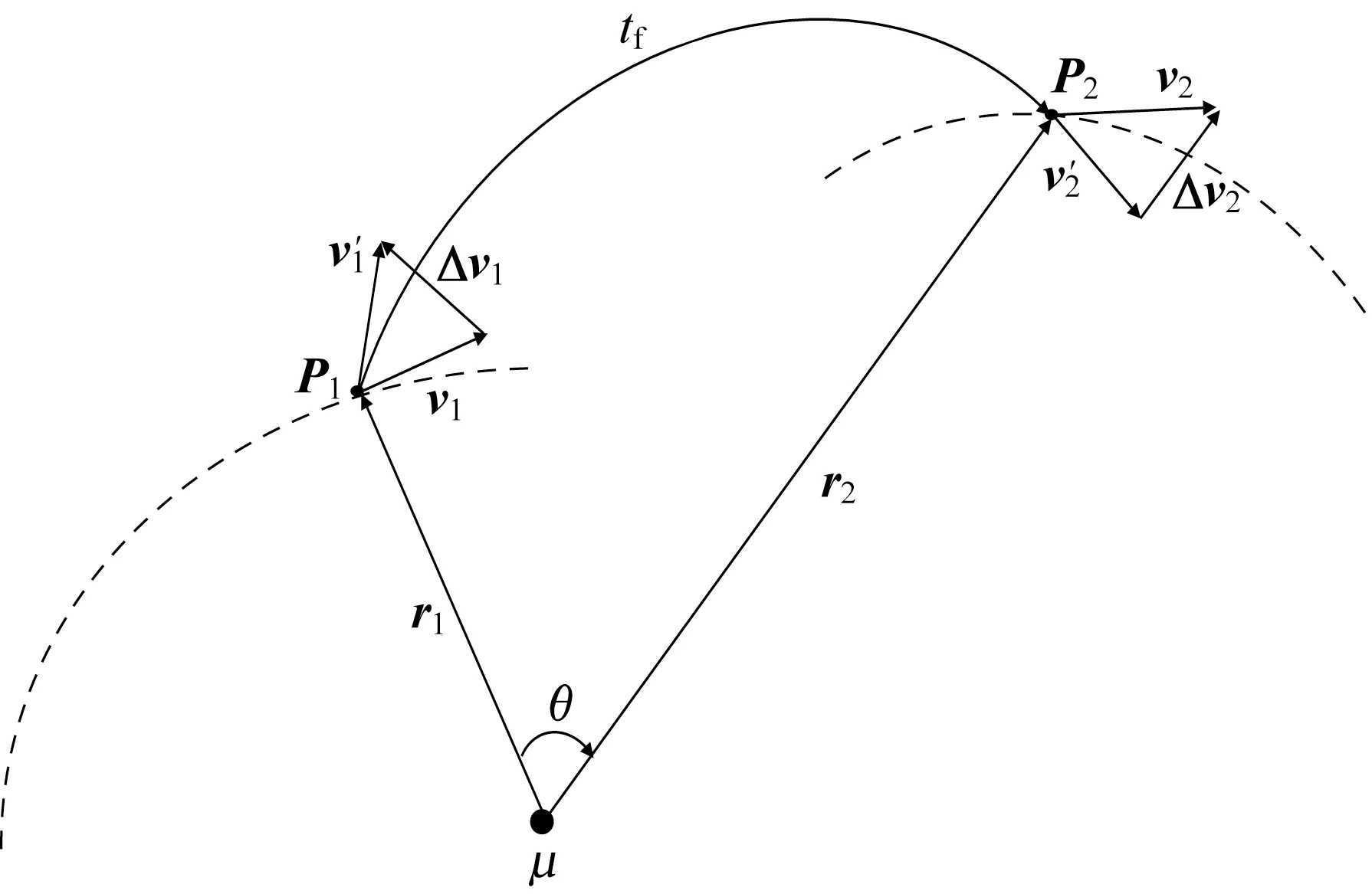
图1 Lambert 转移Fig.1 Schematic diagram of the Lambert transfer

进一步可得到椭圆轨道的半通径，再由半通径确定转移轨道初末2 点、的速度′、′。由此计算转移所需的速度增量为

式中：Δ为机动星在时刻由原轨道进入转移轨道的速度增量；Δ为机动卫星在时刻由转移轨道进入目标星轨道的速度增量。

根据以上关系，建立Lambert 交会方程：

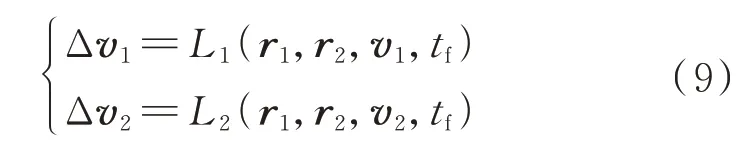
求解Lamber 问题涉及超越方程，只能用迭代法求解。Lambert 转移的求解涉及超越方程，只能通过迭代方式求解，常用的迭代方法有Gauss 迭代法和普适迭代法。Gauss 迭代法是Gauss 在确定谷神星轨道的过程中提出来的经典方法，普适迭代法是Battin 提出的一种对3 类圆锥曲线的方法。当只考虑二体引力的情况下，求解高轨问题时轨道预报产生的误差较大。而现有的Gauss 迭代法、Battin方法等只能解决二体模型下的Lambert 问题，无法处理摄动模型下的Lambert 交会求解。

本文以J2 项摄动模型为例，使用受摄Lambert问题的迭代求解算法，具体流程如图2 所示。具体步骤如下：

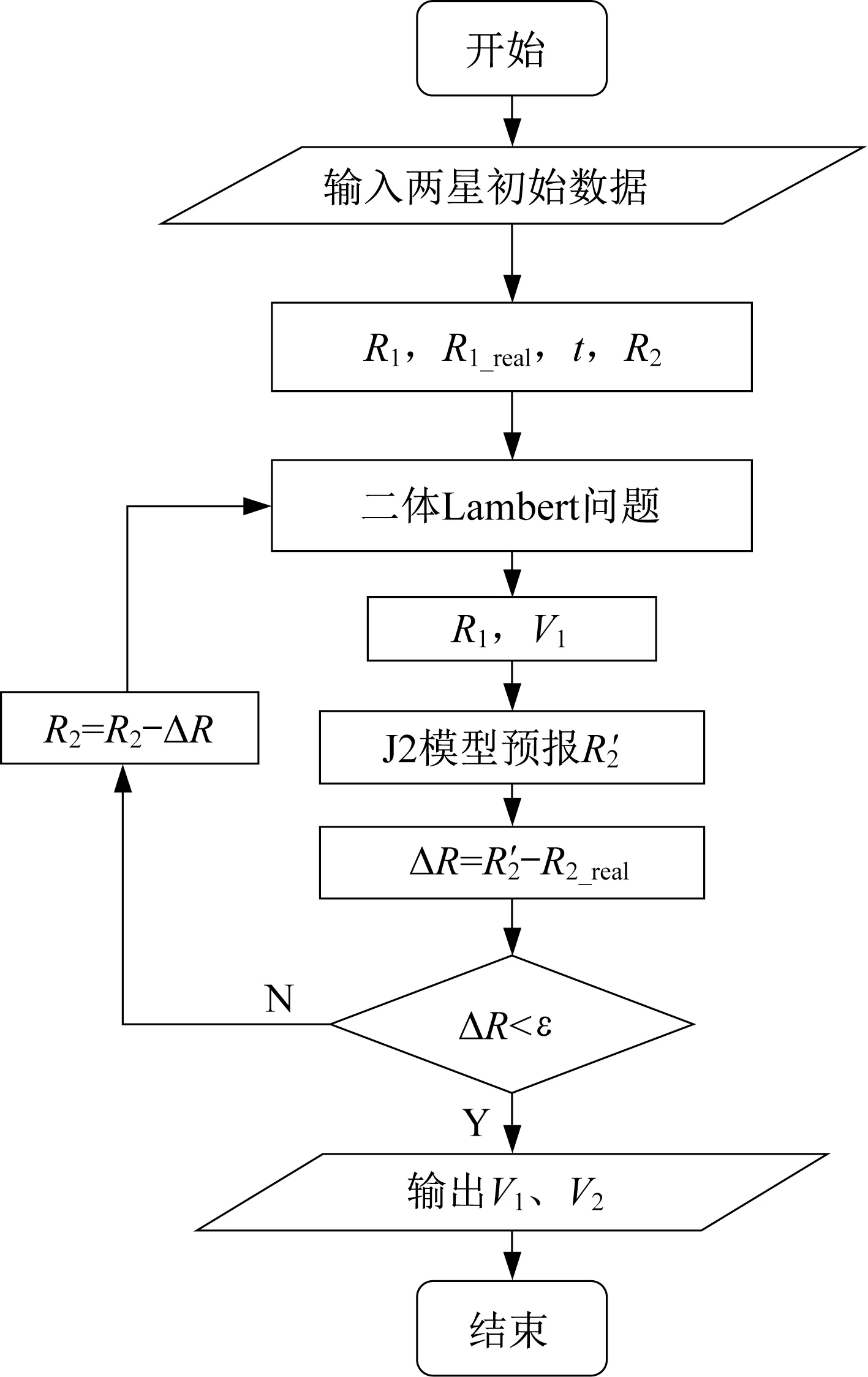
图2 受摄模型的Lambert 问题求解算法Fig.2 Lambert solving algorithm for the perturbed model

给定转移时间，由两星初始数据得出起始位置、目标位置，并赋值迭代目标位置以初值=；

以Battin 方法求解二体Lambert 问题，得到初始位置的速度；

将起始位置和步骤2 得出的初始位置速度，代入J2 模型预报出转移时间之后的卫星位置′；

由于J2 项摄动的影响，时刻卫星实际位置与目标位置存在偏差，求出终端脱靶量Δ=′-；

为了修正偏差，需要对二体Lambert 问题中的目标位置进行修正，以=-Δ作为下一次求解二体Lambert 问题的目标位置。

重复步骤1～5，直到|Δ|＜时，输出转移轨道起始位置和目标位置的速度、。

2 基于Pork-chop 图的单脉冲转移速度增量分析

2.1 Pork-chop 图

Pork-chop图是一种搜索轨道转移窗口的经典方法，被广泛应用于深空任务的设计与规划，也可被借鉴用于高轨抵近任务的优化分析。最早由SERGEYEVSKY 等提出Pork-chop 图，通过给定预期的机动时间和到达时间，对时间组合进行离散网格化，再针对每个二维时间点求解Lambert问题得到对应的速度增量矩阵，即可绘出Pork-chop等高图。

Pork-chop 图可以直观地显示给定时间段内速度冲量大小的变化规律，展示不同出发抵达“时间对”之间的能量对比，为任务决策提供全局参考。速度增量Δ定义为机动前后速度矢量差的模：

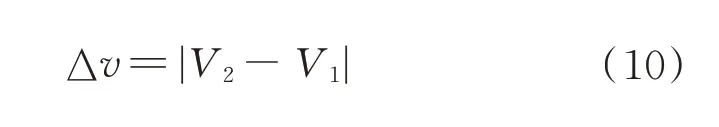
2.2 追踪星转移速度增量分析

对于处于理想地球静止轨道的2 颗卫星来说，由于两星共轨，且相对位置始终保持不变，追踪星拦截目标星的速度增量不随出发时间变化。星下点地理经度相差20°的2 个高轨卫星抵近的Porkchop图如图3所示。

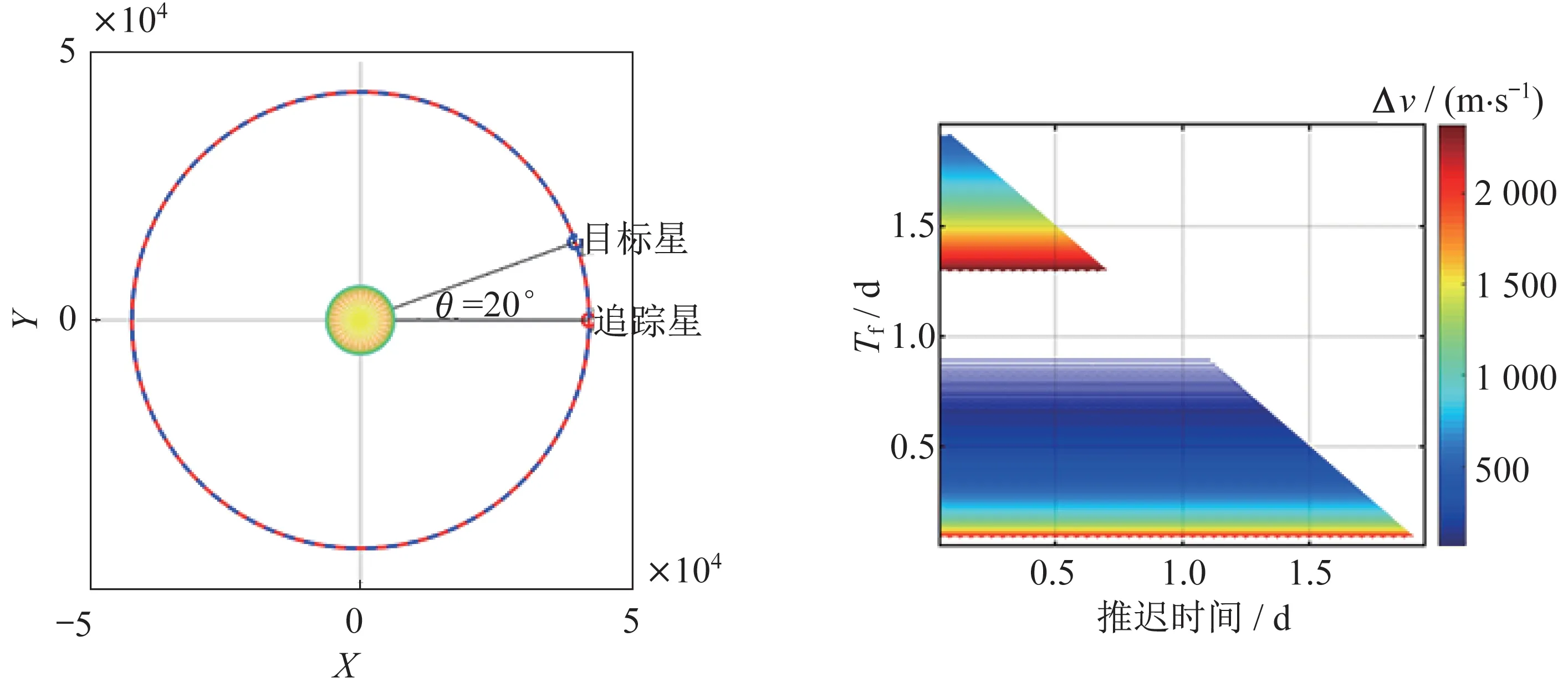
图3 抵近理想GEO 卫星的速度增量Pork-chop 图Fig.3 Pork-chop diagram of velocity increment when approaching the ideal GEO satellite

在图3 中：左侧绘制地惯系轨道图，示意追踪星和目标星初始位置；右侧绘制Pork-chop 图，横坐标为相对初始时刻的延迟出发时间，纵坐标为抵达目标位置的轨道转移时间；颜色条示意消耗速度脉冲的大小。图4～图7 解释同上。由图3 分析可知，地球静止轨道卫星抵近速度增量的大小仅和转移时间相关，与机动时刻不相关。简单来说，在理想GEO上启动抵近任务，任意时刻的燃料消耗都等价。

然而，非合作目标卫星往往不位于理想GEO，其偏心率和轨道倾角都会同静止轨道存在一定偏差。假设追踪星处于地球静止轨道，目标星处于定位点经度与追踪星相差20°的近地球同步轨道。以下分别选取了偏差为=0.01、=0.05、=1°、=10°等目标星轨道进行仿真分析，绘制时间约束为2 d 的Pork-chop 速度增量等高图，如图4～图7所示。

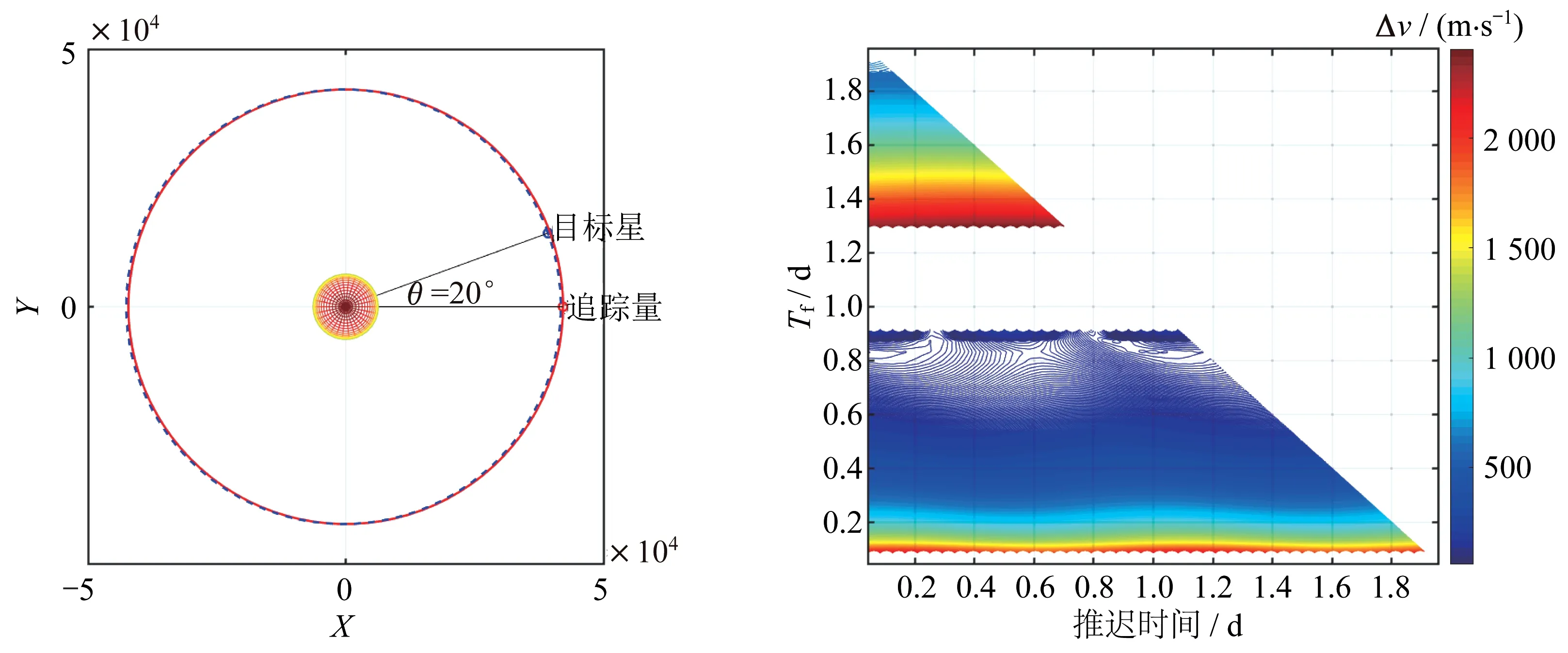
图4 目标星e=0.01 的速度增量Pork-chop 图Fig.4 Pork-chop diagram of velocity increment when the eccentricity of the target satellite is 0.01

图5 目标星e=0.05 的速度增量Pork-chop 图Fig.5 Pork-chop diagram of velocity increment when the eccentricity of the target satellite is 0.05

图6 目标星轨道倾角为1°的速度增量Pork-chop 图Fig.6 Pork-chop diagram of velocity increment when the orbit inclination of the target satellite is 1°

图7 目标星轨道倾角为10°的速度增量Pork-chop 图Fig.7 Pork-chop diagram of velocity increment when the orbit inclination of the target satellite is 10°

可见，当目标星轨道的偏心率或轨道倾角相对静止轨道存在偏差时，最优机动时刻周期性复现规律。该周期为0.5 d，即半个轨道周期。在执行高轨抵近任务时，由于不存在绝对理想的地球静止轨道卫星，任务时间约束内，追踪星何时机动，何时抵达最优，在时间上并不均匀。

3 多脉冲抵近优化设计

3.1 多脉冲抵近的数学模型

多脉冲抵近就是通过在转移过程中多次点火施加速度脉冲的方式，使卫星从初始轨道上的一点转移到目标附近打靶点的抵近方式。本节以三脉冲抵近为例进行建模，整个抵近过程如图8 所示。

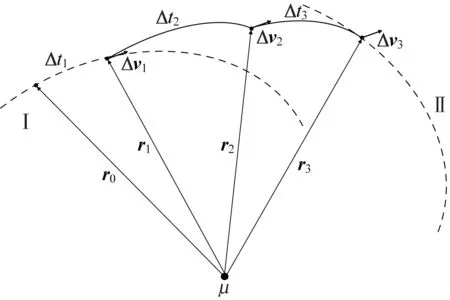
图8 三脉冲抵近Fig.8 Schematic diagram of triple-pulse proximity

假设追踪星位于初始轨道Ⅰ，目标星位于其运行所在的轨道Ⅱ。任务起始时刻，追踪星在地惯系下的空间位置为。经Δ的无动力滑行，至空间位置，第一次点火施加速度脉冲Δ。经Δ的无动力滑行，至空间位置，第二次点火施加速度脉冲Δ。再经Δ的无动力滑行，至目标星附近打靶点位置，实现抵近。最终通过第三次点火施加速度脉冲Δ，进入目标轨道。定义首次速度脉冲Δ为起漂脉冲，末端速度脉冲Δ为刹车脉冲，首末之间的速度脉冲Δ为中间脉冲。已知Ⅰ、Ⅱ轨道参数、任务起始时间和目标附近打靶点，当确定了Δ、Δ、Δ，由于卫星按照式（2）在空间中运行，、、可通过轨道积分确定。当确定了中间脉冲点，通过2.3节方法求解Lambert 问题可得出脉冲Δ、Δ。根据给出的目标附近打靶点参数可求出脉冲Δ。故三脉冲抵近要确定的独立变量有3 个滑行时间以及1 个3 自由度的中间脉冲点坐标，共6 个独立变量。

基于以上分析推广，对于给定目标附近打靶点的脉冲转移问题，转移过程中包含1 个起漂脉冲Δ，-2 个中间脉冲Δ，Δ，…，Δv，以及1 个刹车脉冲Δv。故脉冲抵近要确定的独立变量有个漂移时间Δ，Δ，…，Δt以及-2 个3 自由度中间脉冲点坐标，，…，r，共4-6 个独立变量。

然而，考虑到3 自由度中间脉冲点坐标搜索区间范围过于庞大，导致模型的优化求解难以收敛。本文提出虚拟Lambert 滑行拼接的方法解决该问题。以三脉冲转移为例，寻中间脉冲点时，首先求解漂脉冲位置和刹车脉冲位置在Δ+Δ时间区间内的Lambert 问题，虚拟递推该轨道，并在时刻Δ处取点，作半径为Δ的中间脉冲点寻优域。如此便将中间脉冲点范围很大的地惯系坐标，，…，r，转换为范围较小的相对坐标Δ，Δ，…，Δr，有利于优化算法收敛。中间脉冲点寻优域如图9所示。

图9 中间脉冲点寻优域Fig.9 Schematic diagram of the optimizing domain for the middle pulse point

3.2 约束条件与性能指标

高轨卫星抵近任务中要考虑以下各种约束。

3.2.1 运动状态约束

追踪星在脉冲位置之间按照式（2）运行。以为追踪星状态矢量（3 个位置量和3 个速度量），将式（2）表示(，)，则在脉冲点（包括初始位置和抵近打靶点）之间的运动状态约束可表示为

3.2.2 时间约束

假设任务从起始时刻开始，必须在时间约束Δ内完成抵近。每次施加速度脉冲后的漂移时间（包括起漂脉冲前的等待时间）满足约束：

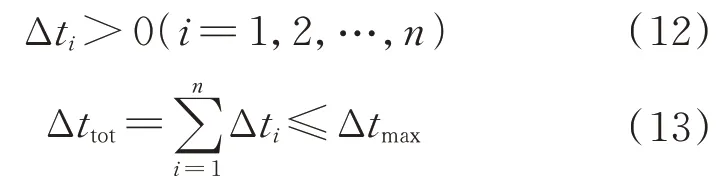
3.2.3 能量约束

追踪星携带燃料有限，假设一次抵近任务所能耗费的最大速度脉冲为Δ，则抵近过程中施加的速度脉冲满足约束：

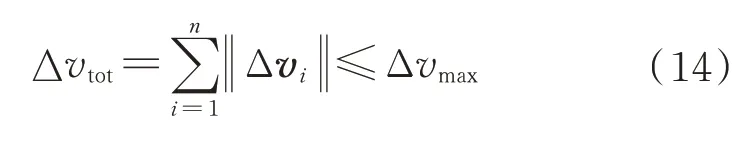
3.2.4 性能指标

以能量消耗最小作为性能指标，表示为

综合以上约束，多脉冲抵近轨迹优化设计的数学模型表示为

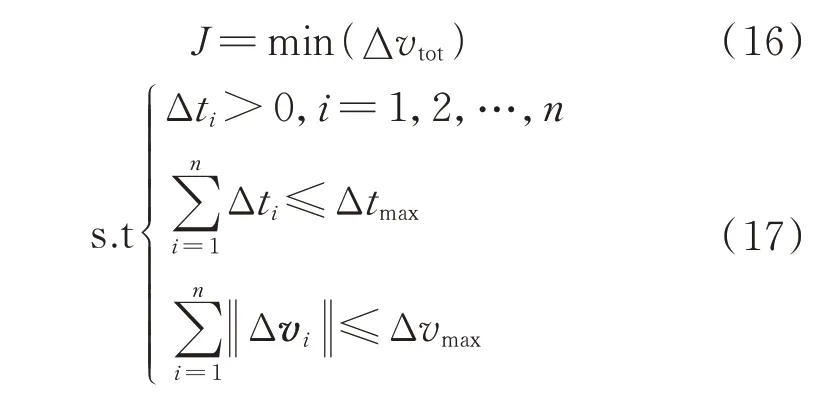
3.3 差分进化算法（DE）

DE由Storn 和Price于1995年首次提出，主要用于求解实数优化问题。该算法是一类基于群体的自适应全局优化算法，属于演化算法的一种，具有结构简单、容易实现、收敛快速、鲁棒性强等特点。DE 的基本思想如下：从一个随机生成的初始种群开始，将种群中任意2 个个体的向量差加上第3 个个体的和生成新的个体，然后将这个新的个体与种群中相应的当代个体相比较，如果新个体的适应度优于当前个体的适应度，则是在下一代个体中取新替换旧，或仍保持旧个体。通过不断的进化，可以保留好的个体，淘汰差的个体，引导搜索接近最优解。其具体进化步骤如下：

首先确定DE 的控制参数，确定其适应度函数。DE 控制参数主要包括：种群大小、缩放因子与交叉概率；

随机产生初始种群；

根据适应度函数对初始种群进行评价，计算种群中个体的适应度函数值；

判断终止条件或进化代数是否达到最大，若是则停止进化搜索，将搜索到的最佳个体作为最优解进行输出，若否则继续进化；

进行变异和交叉操作，得到中间种群；

在原种群和中间种群中选择个体，得到新一代种群；

进化代数=+1，转步骤4。

在DE 的主要控制参数中，种群规模在算法中主要反映了种群信息的大小。值越大，种群信息越丰富。但结果会使计算量变大，不利于求解。相反，种群多样性是有限的，这不利于算法获得全局最优解，甚至导致搜索停滞。交叉概率主要反映后代与父代之间以及交叉过程中中间变异个体之间的信息交换量。值越大，信息交换程度越高。相反，如果值过小，种群多样性会迅速下降，不利于整体优化。与相比，缩放因子对算法性能的影响更大，主要影响算法的全局优化能力。越小，算法的局部搜索能力越好。

4 仿真算例

假设任务起始时间为UTC 时2021 年4 月1 日12：00：00.000，追踪星和目标星都处于近地球静止轨道。任务初始时刻，追踪星和目标星的瞬时轨道根数如下：

式中：为近地点幅角；为升交点赤经；为真近点角。

不考虑入轨相对构型，假设以目标星位置作为打靶点，目标星轨道作为打靶轨道，分别对不同时间约束下的双脉冲抵近、三脉冲抵近和四脉冲抵近进行轨道优化求解。设置DE 的种群规模=12，缩放因子=0.85，交叉概率=0.85。设置最大迭代次数为100，并对每组输入数据进行5 组优化计算实验。当任务时间约束分别为12、24、48 h 时，仿真结果见表1～表3。24 h 时间约束下的双脉冲抵近、三脉冲抵近和四脉冲抵近的轨迹图如图10～图12 所示。

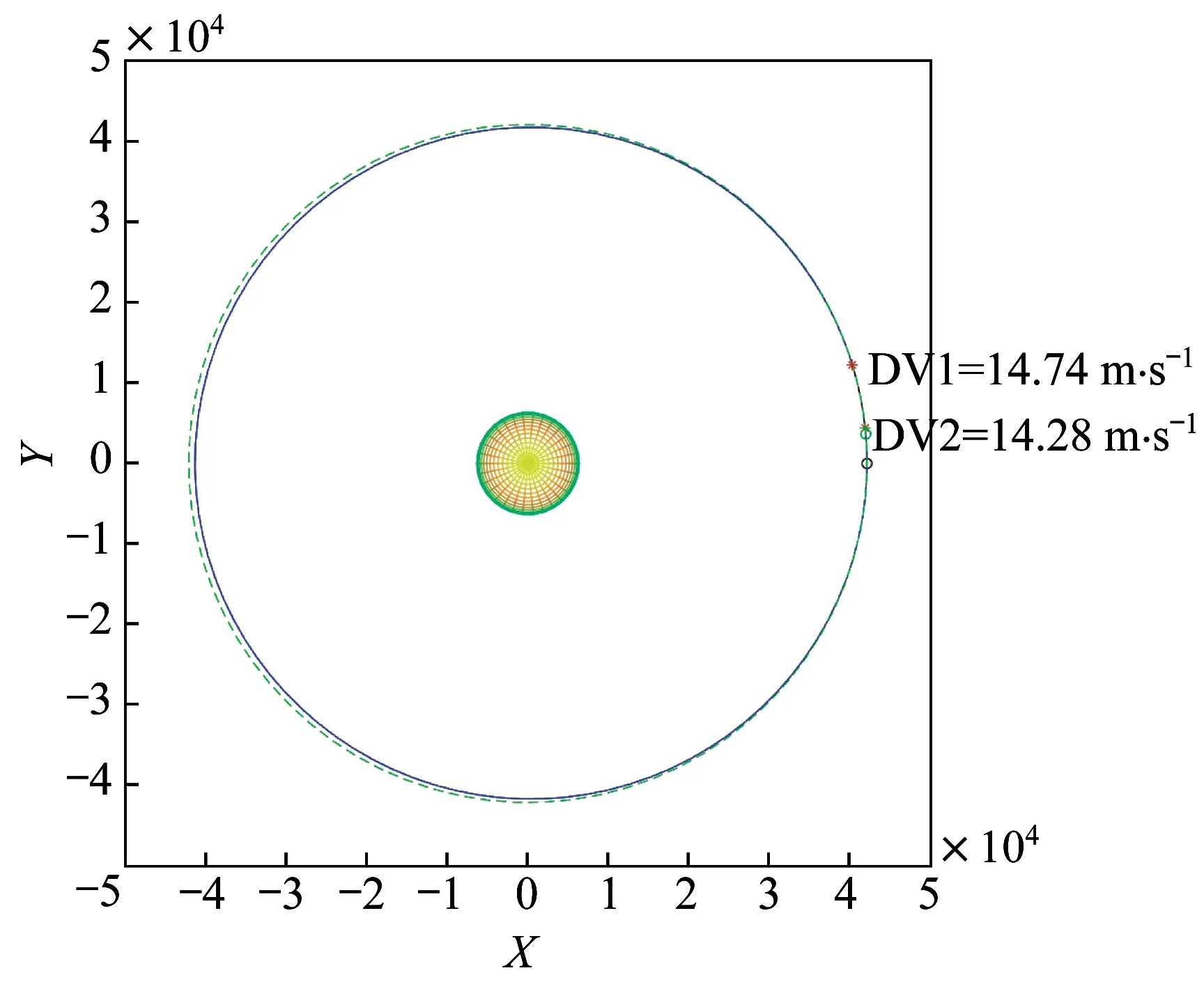
图10 24 h 约束下双脉冲抵近优化算例Fig.10 Schematic diagram of the dual-pulse proximity optimization example under the 24 h constraint

表1 12 h 约束的仿真数据Tab.1 Simulation data under the 12 h constraint

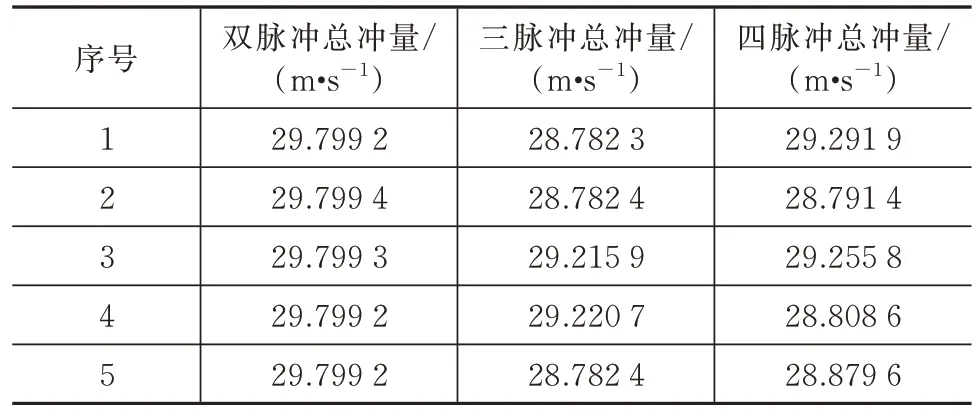
表2 24 h 约束的仿真数据Tab.2 Simulation data under the 24 h constraint

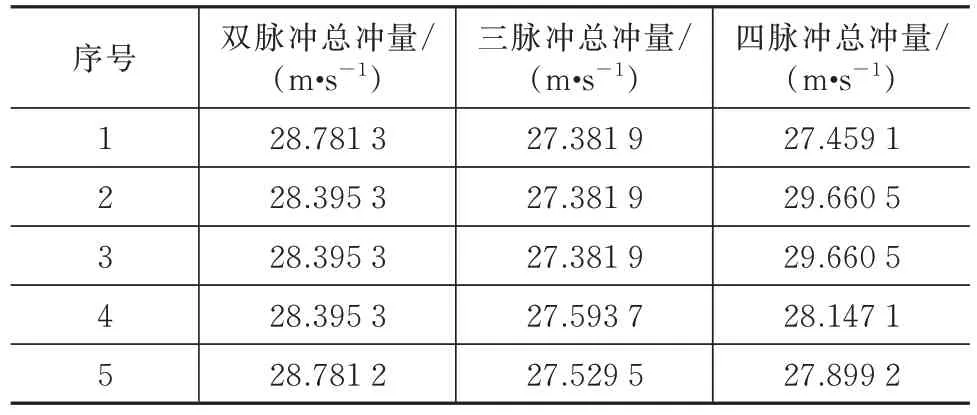
表3 48 h 约束的仿真数据Tab.3 Simulation data under the 48 h constraint

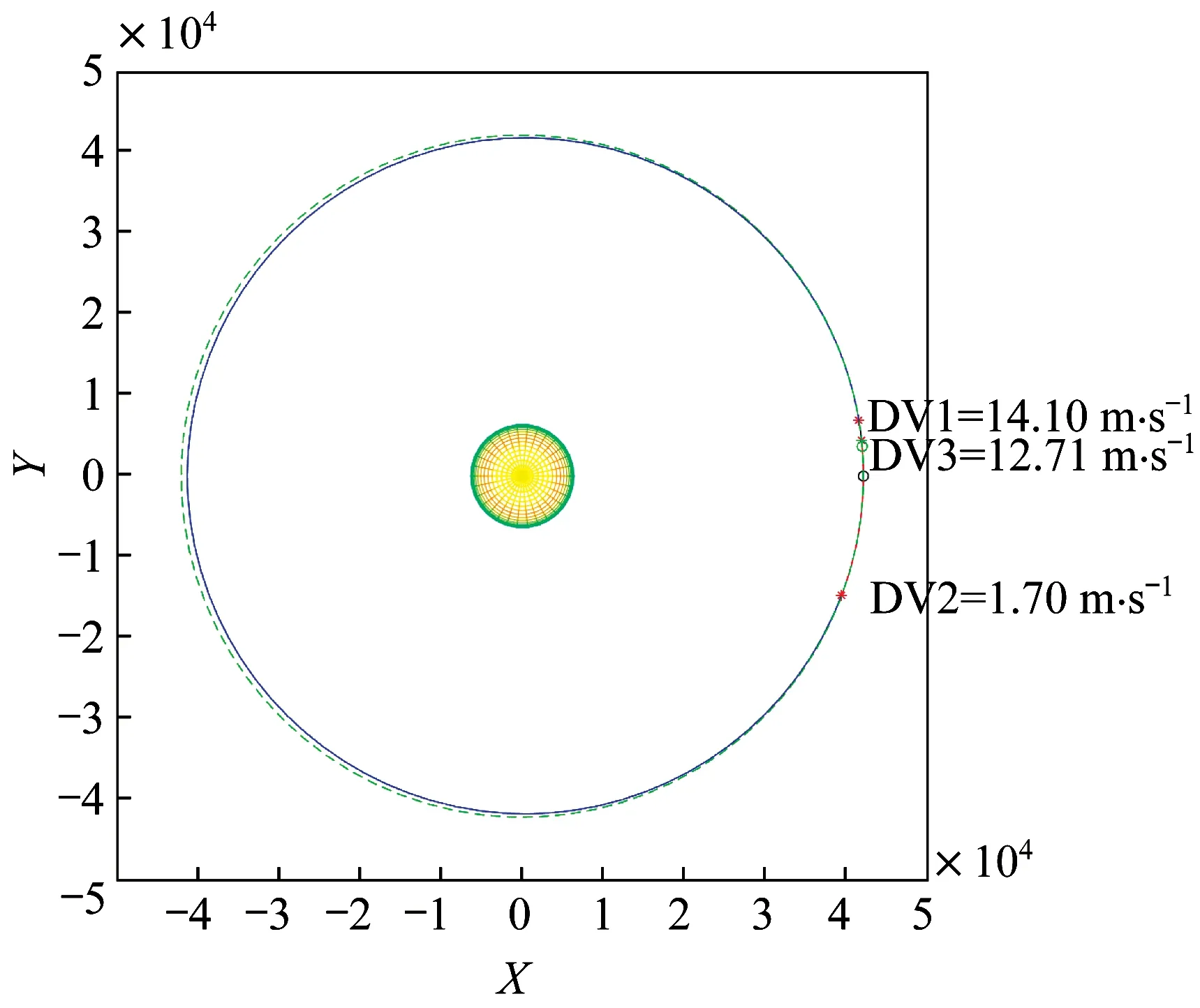
图11 24 h 约束下三脉冲抵近优化算例Fig.11 Schematic diagram of the triple-pulse proximity optimization example under the 24 h constraint

图10～图12 中标注的DV1、DV2、DV3 和DV4分别指第1 次脉冲大小、第2 次脉冲大小、第3 次脉冲大小和第4 次脉冲大小，对应红色星号示意施加脉冲的位置。

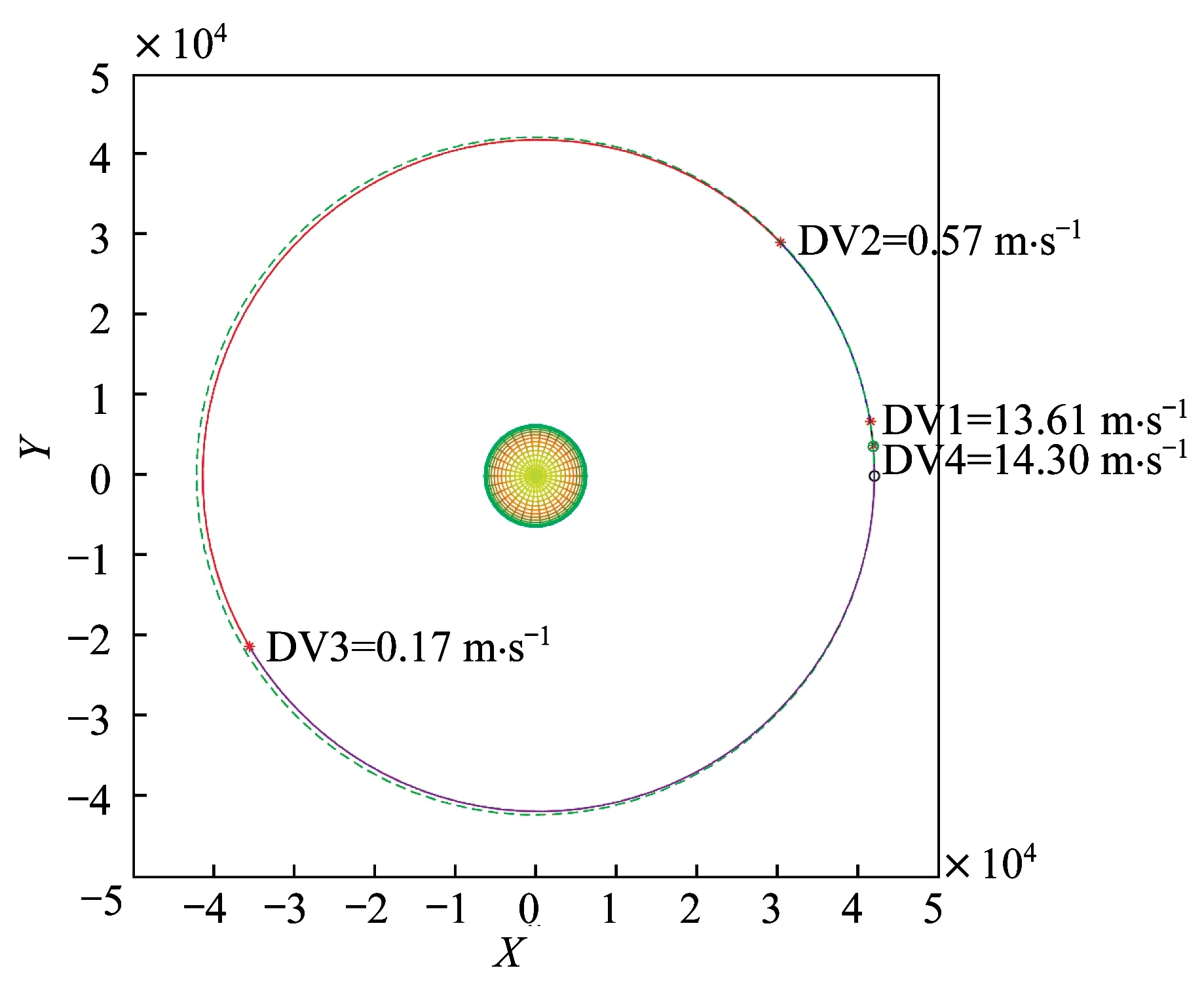
图12 24 h 约束下四脉冲抵近优化算例Fig.12 Schematic diagram of the quadruple-pulse proximity optimization example under the 24 h constraint

由以上算例可以总结出：1）延长任务约束时间可以有效降低总冲量；2）三种脉冲次数的转移方式的优化结果，耗费总冲量相差较小；3）在中短期抵近任务中，双脉冲转移由于独立变量少所以最优解稳定易得，四脉冲转移优化收敛性较差，而三脉冲转移优化效果相对较好。

5 结束语

本文对高轨卫星远程抵近问题建立了数学模型，使用Pork-chop 图探讨了非理想地球静止轨道偏心率和轨道倾角偏差对拦截速度增量的影响，分析了任务时间约束内远程抵近轨道最优解的分布规律。给出多脉冲抵近问题涉及的独立变量、约束条件和目标函数，建立了多脉冲抵近轨道优化设计的数学模型。最后使用DE，通过多组算例对该问题进行优化求解，得出三脉冲抵近方案在中短期任务中优化效果相对较好的结论。