冗余空间机械臂试探性搜索障碍规避策略

张崇峰，陈敏花，侯月阳，张文婧

（1.上海航天技术研究院，上海 201109；2.上海航天控制技术研究所，上海 201109；3.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

冗余空间机械臂具有比空间维数更多的自由度，在空间轨迹规划和空间避障方面具有更多的选择和灵活度，适合完成在轨服务、维护维修任务中的目标抓捕和精细操作，具有广泛的应用前景和巨大的研究意义，成为研究的热点。

根据发展时间进行划分，避障算法可分为2 类传统方法：典型的有基于构形空间的几何法和拓扑法、图搜索法、人工势场法等；智能方法主要有遗传算法、人工神经网络法、模糊逻辑法、梯度投影法和改进的梯度投影法，以及这些方法的混合方法等。

LOZANO-PEREZ提出，将机械臂的工作空间分为自由空间和障碍空间，并在自由空间内利用启发式搜索算法寻找机械臂的运动路径。在众多启发式算法中，快速扩展随机树算法特别适合多自由度机器人的运动规划问题。BERTRAM 等提出了一种路径规划过程中的目标选择方法，该方法保证了新生长的节点不断向着目标点生长。STILMAN对快速扩展随机树算法进行了改进，使得末端轨迹能够满足特定的约束条件，但是快速扩展随机树算法搜索效率较低，不具有实时性。ZHAO 等已经成功地运用基于构型空间，即C 空间的几何法使得机械手绕开障碍物顺利采摘到水果。周芳等提出了一种路径规划算法，是基于C 空间分解路标法，将路标图的搜索维数由六维降为三维，使路标图的搜索空间大大减少，该方法不仅缩短了在线实时规划的时间，还提高了路径规划的成功率。

人工势场法的基本思想是在机械臂的C 空间中构造一个人工势场，使得在该势场中运动的机械臂受到其目标位姿点引力场和C 空间障碍周围斥力场的共同作用，无碰撞轨迹规划可以通过搜索函数的下降方向实现。尽管其是一种局部规划方法，但由于便于数学描述且适用于多自由度机械臂，使用非常广泛。

学者们努力将机器学习功能引入到现在的机器人中，使机器人更加智能化，由于环境复杂多变，这种方法在路径规划方面通常与其他一些算法结合使用。GAUTAM 等提出了一种基于遗传算法和神经网络算法结合的方法，该算法能够使无人机在三维环境下准确避障，具有良好的效果。

人工势场法存在局部最小问题，更适用于移动机器人的无碰撞轨迹规划问题，而机器学习方法计算量大，不适用于计算资源紧张的空间机械臂。C空间法是一种全局规划方法，通过求解整个C 空间，使得自由空间、障碍空间一目了然，因而可以按任何性能指标搜索路径，且具有完备解。然而在实际应用中C 空间法存在2 个问题：1）对于多自由度的机械臂来说，求解整个C 空间需要很大的计算量，计算时间随自由度的增加而呈指数级增长；2）C 空间中的障碍空间无法获得解析表达式，只能通过离散化得到。以上这些问题限制了C 空间方法在空间机械臂中的应用，因此，需要针对空间机械臂的工程要求和实际背景，对现有成果进行改进，获得高效实用的无碰撞轨迹规划算法。本文首先介绍碰撞检测算法，进一步研究无碰撞目标构型求解方案，提出无碰撞路径试探性搜索算法并仿真验证方法的有效性。

1 碰撞检测算法

碰撞检测算法是无碰撞的目标构型求解算法和无碰撞的路径搜索算法运行的基础。碰撞检测算法是在工作空间中进行的，可以测量得到机械臂的各个关节角，并通过运动学关系求得机械臂上各个点在中心体体坐标系中的位置，而工作空间中的障碍物在中心体体坐标系中的位置可以通过相关敏感器测量得到，这样就具备了在工作空间进行碰撞检测的前提条件。

碰撞检测算法是近似和多层次的。近似是指为了简化检测的计算量，对机械臂和障碍物进行了一定的简化处理。真实的机械臂由单自由度关节铰接在一起的7 段圆柱体构成，算法将其简化为连接各个关节轴的线段，对舍去的部分，可以通过适当扩大障碍物的边界加以修正，这样的处理方法是方便的，也是符合工程实际和工程要求的。多层次是指这种碰撞检测算法提出了3 个层次的碰撞检测问题，并通过对时间或空间离散化的方法，逐步简化，将高层次的碰撞检测问题转化为低层次的碰撞检测问题，符合工程实际和工程要求。

这3 个层次为机械臂运动的碰撞检测、机械臂构型的碰撞检测、机械臂上一点的碰撞检测。首先将机械臂的运动过程进行时间上的离散化，即将构型连续变化的机械臂运动过程，离散为有限多个固定的机械臂构型。在构型空间中，将表示运动过程的连续曲线，离散为有限多个点，从而将运动过程的碰撞检测问题转化为有限多个机械臂构型的碰撞检测问题。只要任意一个构型的机械臂与障碍物相碰，则整个运动过程是与障碍物相碰的，在构型空间中这个运动的轨迹与构型空间障碍物相交。接着对机械臂进行空间上的离散化，将处于某一构型的机械臂用几条线段来表示，进而将这些线段离散化为一系列的有限多个点，将机械臂构型的碰撞检测问题转化为有限多个点的碰撞检测问题。如果这些点中存在位于障碍物内部的点，则认为该机械臂构型是与障碍物碰撞的，在构型空间中，表示该构型的点位于构型空间障碍物内部。

由此可知，碰撞检测算法的基本问题是如何判断一个点是否在障碍物之内。采用凸多面体矢量内积检测算法，对于障碍物，总可以找到一个凸多面体的包络，或者把障碍物分成几部分，每一部分找到一个凸多面体的包络，然后用这些凸多面体近似代替障碍物本身。记某个凸多面体的第个面的中心点为P，第个面的外法线矢量为n，记待检测的点为，点位于这个凸多面体的充分必要条件是：对于凸多面体的所有的面都有

凸多面体判断如图1 所示。点只要位于其中一个凸多面体之内，就认为点位于障碍物之内。利用碰撞检测算法，可以判断机械臂的某个运动过程或某个构型是否与障碍物相碰。在此基础上可以运行无碰撞的目标构型求解算法和无碰撞的路径搜索算法。

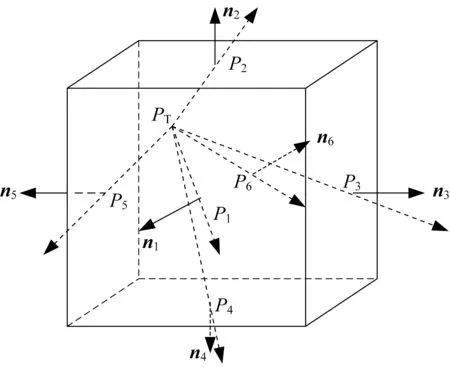
图1 凸多面体Fig.1 Schematic diagram of the convex polyhedron

2 无碰撞目标构型求解算法

无碰撞目标构型求解算法的主要思路是：首先，由任意初始构型通过运动学轨迹规划算法，得到一个满足机械臂末端位置姿态要求的目标构型；然后，对目标构型进行碰撞检测，如果没有碰撞，则将这个目标构型作为最终的无碰撞目标构型；如果发生碰撞，则在这个目标构型附近对各个关节角进行微小调整，并对调整之后的目标构型反复进行碰撞检测，直到不发生碰撞为止，将得到的目标构型作为最终的无碰撞目标构型。

在对关节角进行微调时，采取的方法为：在碰撞构型下，改变某个关节角，得到新的构型；将新的构型作为假想的初始构型，通过运动学轨迹规划算法得到新的目标构型，并对其进行碰撞检测；如发生碰撞，则继续改变该关节角的大小，直到得到的目标构型不与障碍物碰撞为止。在构型空间中，该方法就是沿某个坐标轴的方向进行搜索的算法。

一般全方位机械臂为6 自由度，在需要避障的场景下需要增加自由度，即7 自由度机械臂，也可称为冗余机械臂。

2.1 机械臂运动学算法

7 自由度机械臂速度级正运动学方程如下：

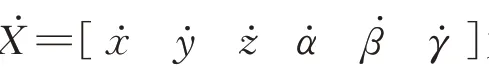
7 自由度机械臂速度级逆运动学方程如下：

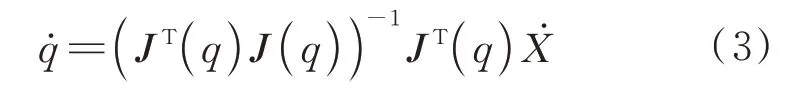
式中：()为雅克比矩阵的转置。

7 自由度机械臂有无数多组解，固定7 自由度机械臂的某个关节，使机械臂暂时退化为6 自由度，逆运动学求解方法简化为

如果对固定的关节角进行搜索，可以通过6 自由度逆运动学求解算法对机械臂7 自由度逆运动学的无数个解进行搜索，这是无碰撞目标构型求解算法的基本思路。

2.2 无碰撞目标构型求解算法

无碰撞目标构型求解算法流程如图2 所示。算法左侧部分只运行一次，如果求解成功，则算法运行结束；如果失败则转至运行右侧部分，右侧为一个循环，不断搜索满足末端作用器位置和姿态的机械臂构型，直至找到无碰撞的目标构型作为最终结果输出。若算法由左侧部分转至了右侧部分，则将左侧部分的积分结果作为搜索的起始构型，不断改变其第一个关节角的角度，作为7 自由度逆运动学求解算法的积分初值构型，直至找到一个与障碍物不碰撞，且积分过程中无奇异的目标构型。如果算法在右侧部分循环了很多次仍没有找到合乎要求的目标构型，则可以改变算法最初的积分初值，重新运行该算法。

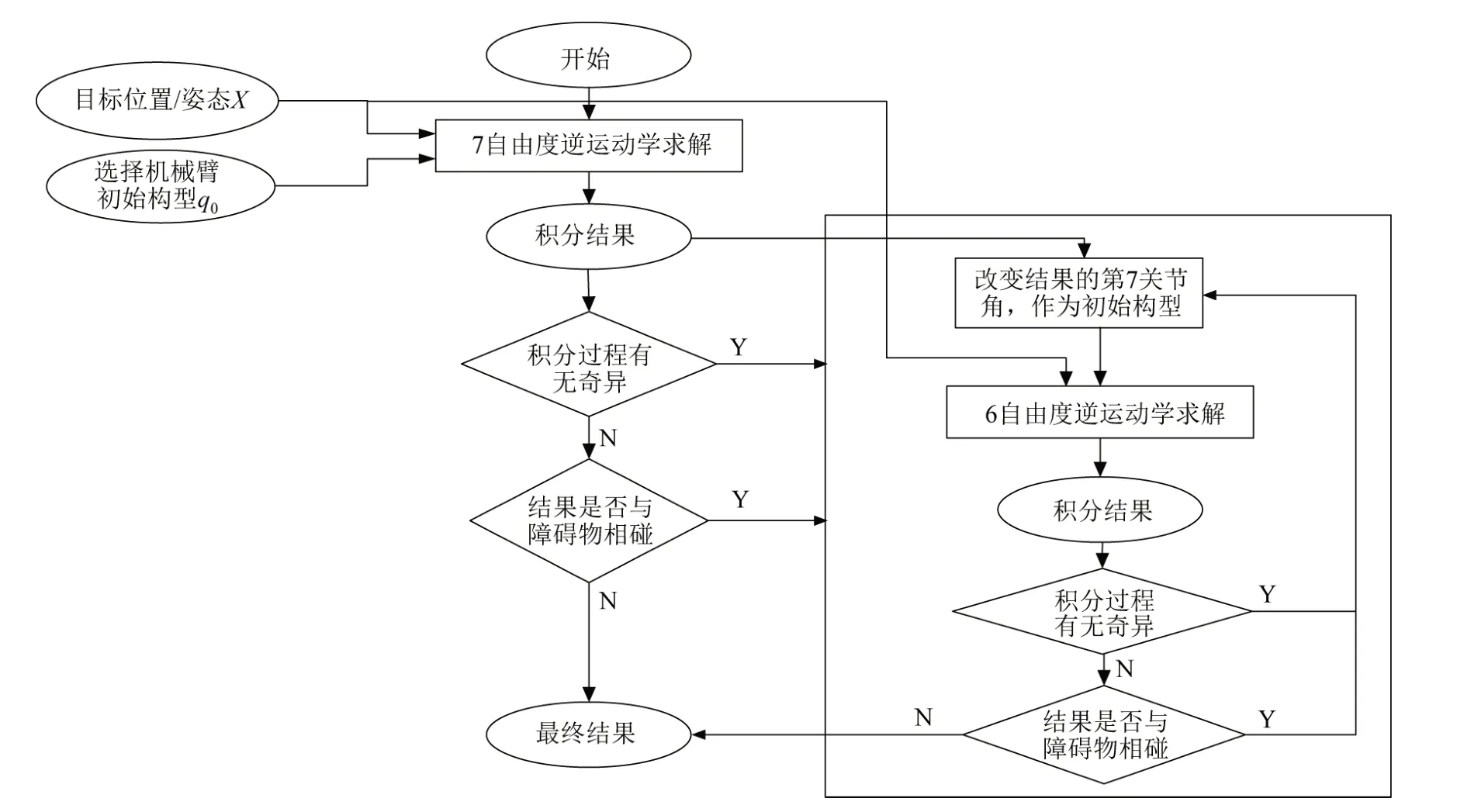
图2 无碰撞构型求解算法Fig.2 Configuration algorithm without obstacles

下面选取一个算例，验证无碰撞目标构型求解算法的有效性。给出机械臂的构型及自由度配置，各节机械臂的旋转轴指向（箭头所指为右手定则正向）如图3 所示，图中的构型为机械臂转角均为零时的状态。各节机械臂的几何尺寸如图4 所示，图中各尺寸的基准为机械臂各轴的轴线。系统中各节臂的安装点位置参数见表1。

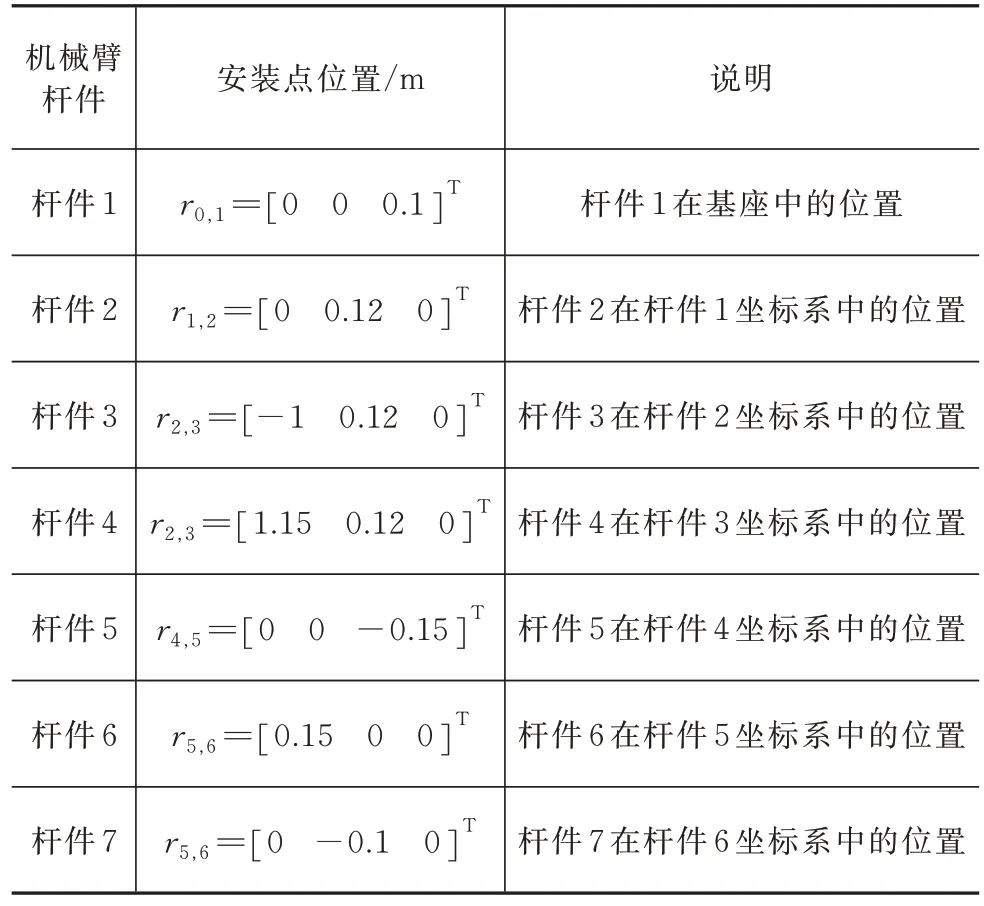
表1 机械臂杆件参数Tab.1 Position parameters of the manipulator bars

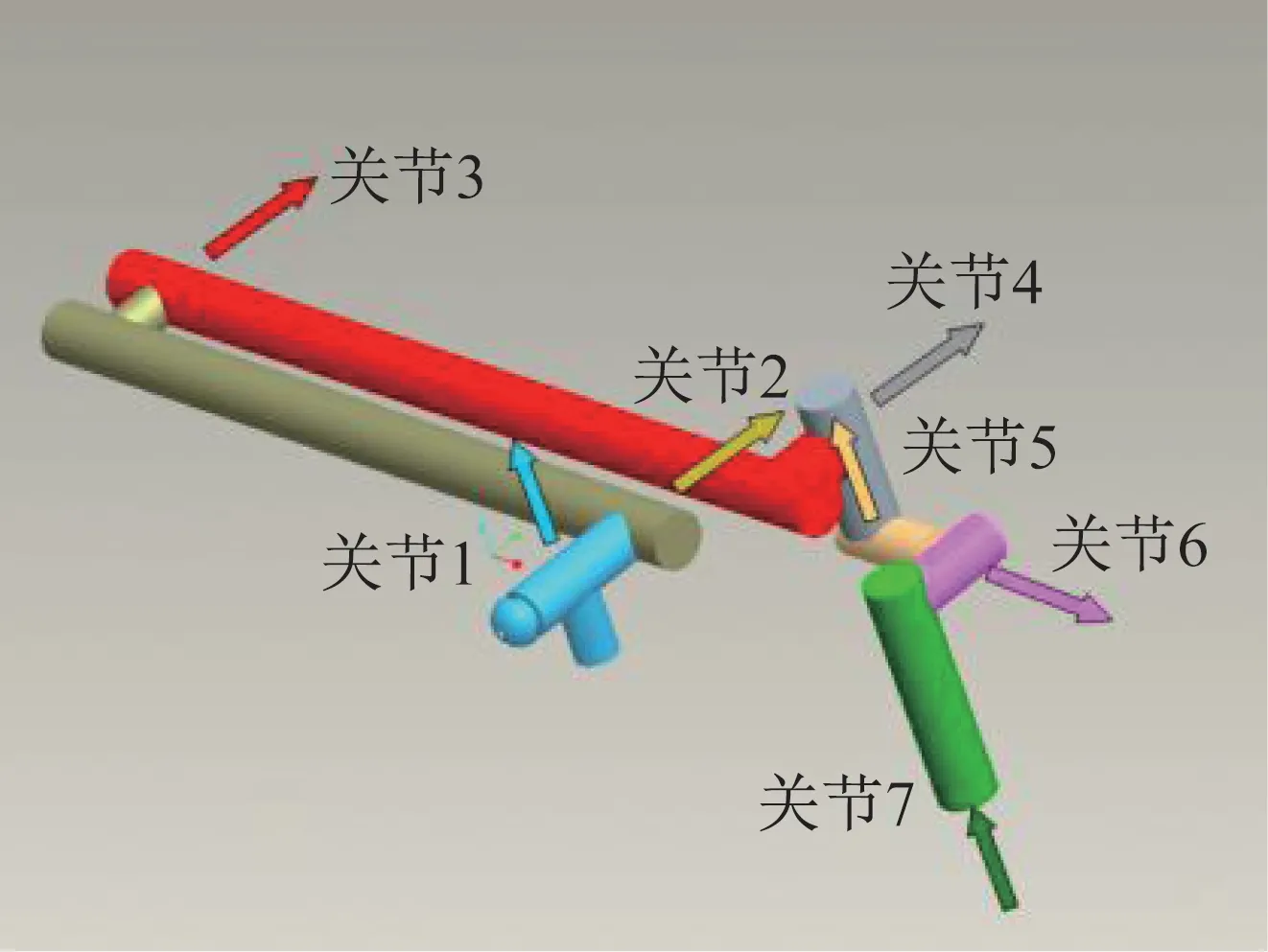
图3 机械臂各轴旋转方向Fig.3 Schematic diagram of the circumvolve directions of the manipulator

图4 机械臂几何尺寸Fig.4 Geometrical dimensions of the manipulator

目标位姿：（2.0 m，0.3 m，0.5 m，-0.2，0.5，0）。障碍物参数：立方体顶点坐标为（1.5，-0.2，0）、（1.5，-0.2，0.5）、（1.5，0.3，0）、（1.5，0.3，0.5）、（2，-0.2，0）、（2，-0.2，0.5）、（2，0.3，0）、（2，0.3，0.5）。初始积分关节 角：-1.570 7、3.141 4、1、0、0、0、0。积分时间：60 s。

右侧部分积分初值的搜索方法为在左侧部分积分结果的周围以0.03为步长改变第一个关节角，作为右侧部分的积分初值，即′=+0.03，=0，1，-1，2，-2，3，-3，…，当=0 时即是左侧部分的积分结果，算法的搜索过程见表2。

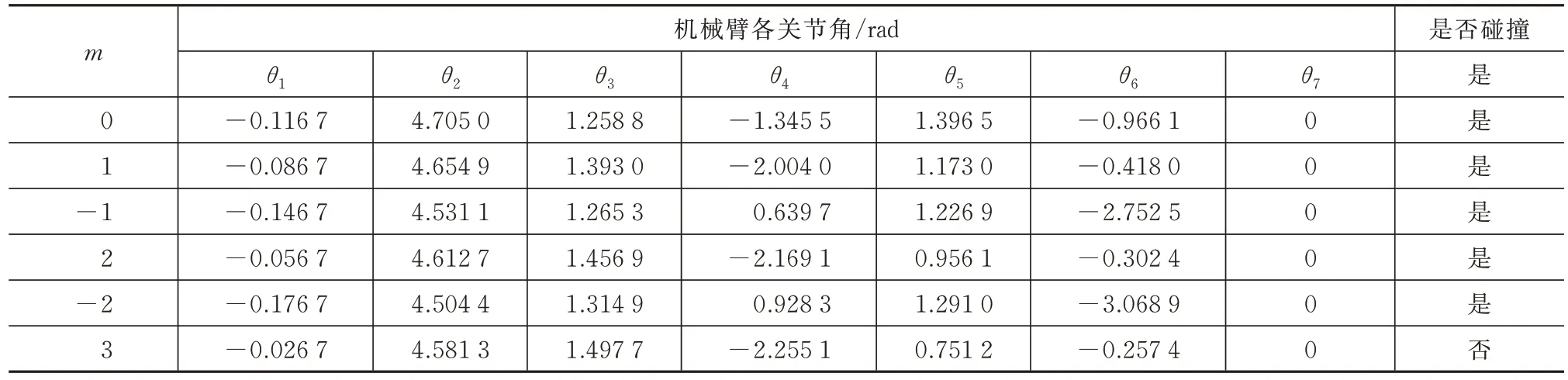
表2 搜索结果Tab.2 Search results

由表1 可知，算法左侧的积分结果是与障碍物相碰的，然后算法转至右侧部分，右侧部分在左侧的积分结果周围搜索，最终当=3，即=-0.026 7时，求得了一个不与障碍物相碰且积分过程无奇异的构型。得到无碰撞目标构型后，可在构型空间中进行无碰撞的路径搜索。

3 无碰撞路径试探性搜索算法

对于空间机器人的中央控制器来说，由于需要求解的构型空间是7 个自由度的，计算负载相当大，所以需要一种不需求解整个构型空间的路径搜索算法。本文提出一种试探性搜索算法，由起始构型按照某一规律不断向目标构型运动，如果运动过程中发生碰撞，则调整前进的方向，直到找到一条不与障碍物发生碰撞的路径。这样，就不用求解整个构型空间，而只需进行碰撞检测。于是，路径搜索算法转变为了3 个子问题：1）如何设计在构型空间中的试探规律；2）碰撞检测；3）发生碰撞后如何调整。碰撞检测问题已解决，介绍另外2 个问题的解决方案。

在构型空间中，任意两点之间都可以用若干条平行于坐标轴的折线来连结。在有障碍物时，如果存在无碰撞的路径，则该路径一定也可以用若干条平行于坐标轴的折线来近似，且近似之后的折线路径也不与障碍物发生碰撞。一个二维构型空间中的例子，如图5 所示。S 为初始构型，E 为目标构型，C1、C2、C3 均为障碍物。

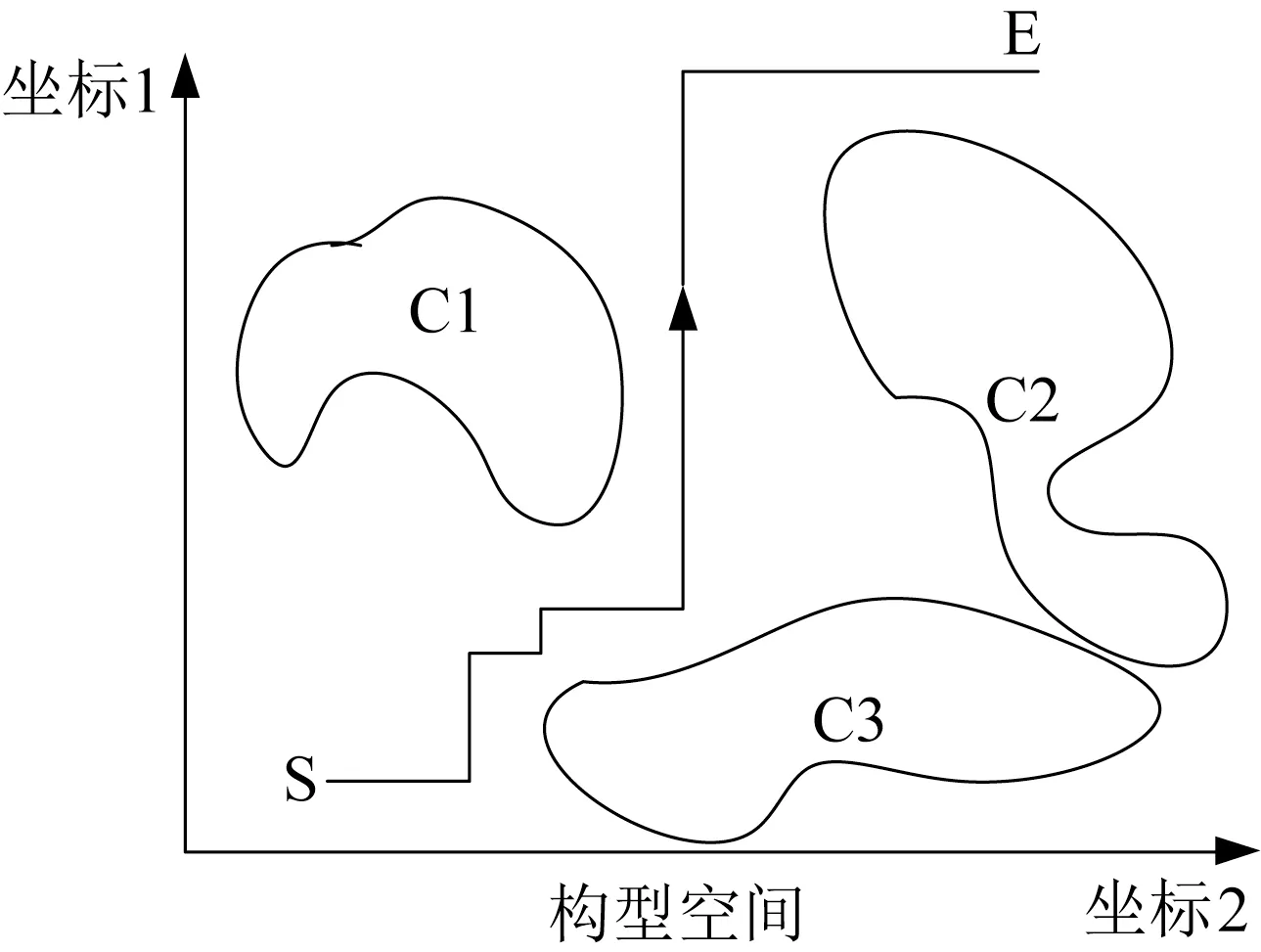
图5 二维构型空间路径Fig.5 Path in two-dimensional configuration space

对于一个存在障碍的构型空间以及确定的路径起点S 和终点E，总可以找到一个足够大的正整数，能够将路径分割得足够细，使得由该路径分割常数构造的·个子运动，经过一定的顺序安排后，可以组成一条连接点S 和E 点的无碰撞轨迹。因此，试探性路径搜索算法的关键就是通过试探的方法找到一个子运动的顺序。即相当于已知有个运动方向，以及沿每个方向上的个子运动，要求以某种顺序将这些子运动进行排列，使得这些子运动连起来形成的路径不与障碍物相碰。

假设以1，2，…，分别为沿个坐标轴方向上的子运动，试探规律为沿坐标轴方向依次进行试探，即子运动的试探顺序为1，2，…，，1，2，…，，…，1，2，…，。如果第步试探发生碰撞，则将这一步的子运动调整到序列末尾，并沿下一个坐标方向进行试探。如果所有方向的试探结果均为碰撞，则返回上一步，并认为-1 步发生碰撞（虽然该步碰撞检测结果为不碰撞），并沿-1 步的下一个坐标方向进行试探。如此循环，直到整个序列不发生碰撞为止。如果无法得到无碰撞序列，则应取更大的，重新进行试探。算法流程如图6 所示。

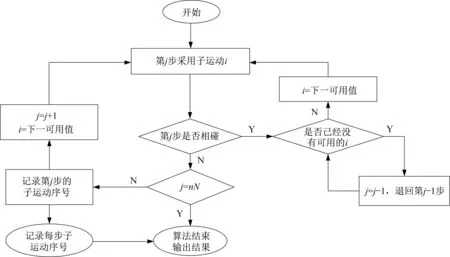
图6 试探性搜索算法Fig.6 Tentative search algorithm

下面验证路径搜索算法的有效性和正确性。初始构型和目标构型的参数见表3。障碍物中心点位置坐标为[1.2 -0.8 1.7]，初始构型和目标构型示意图如图7 所示。路径分割常数=10。下面给出算法的搜索结果，试探次数为70 次，输出的子运动序列见表4。

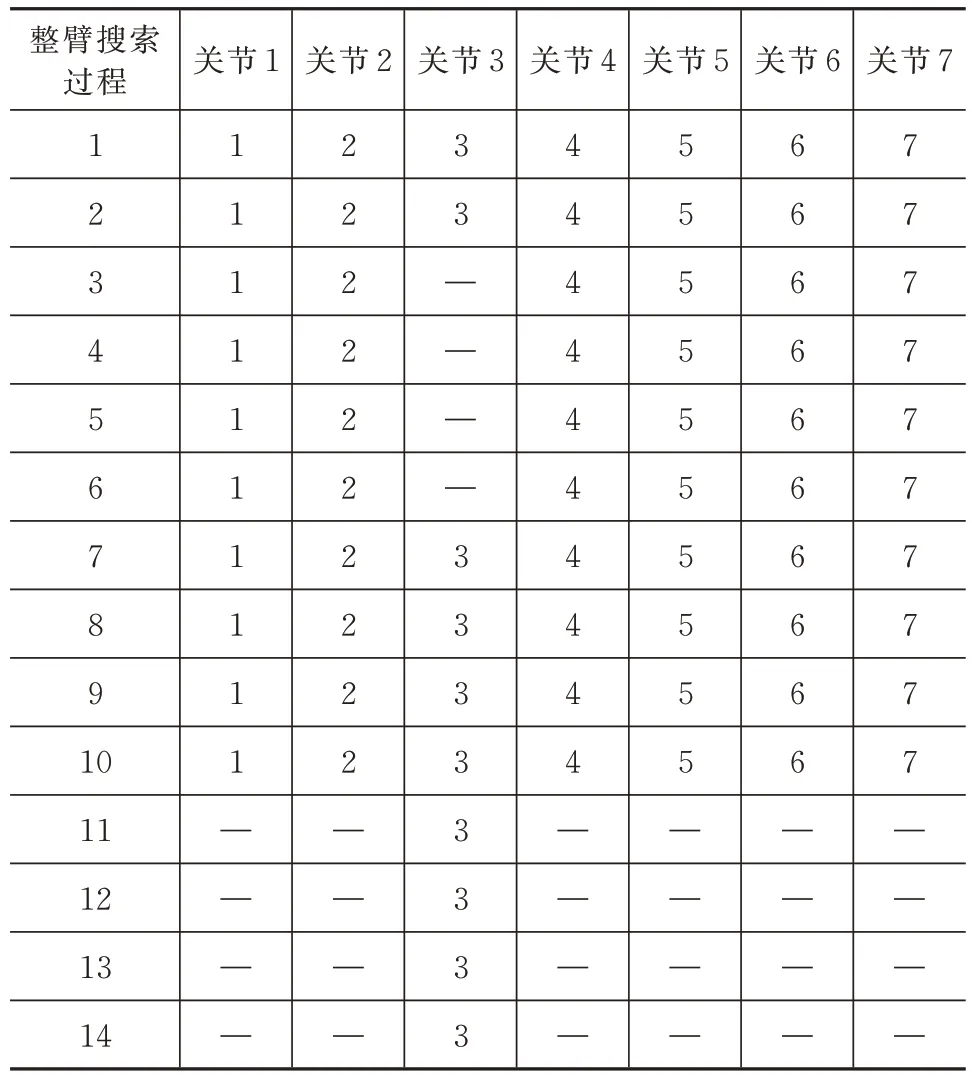
表4 子运动序列Tab.4 Child motion sequence

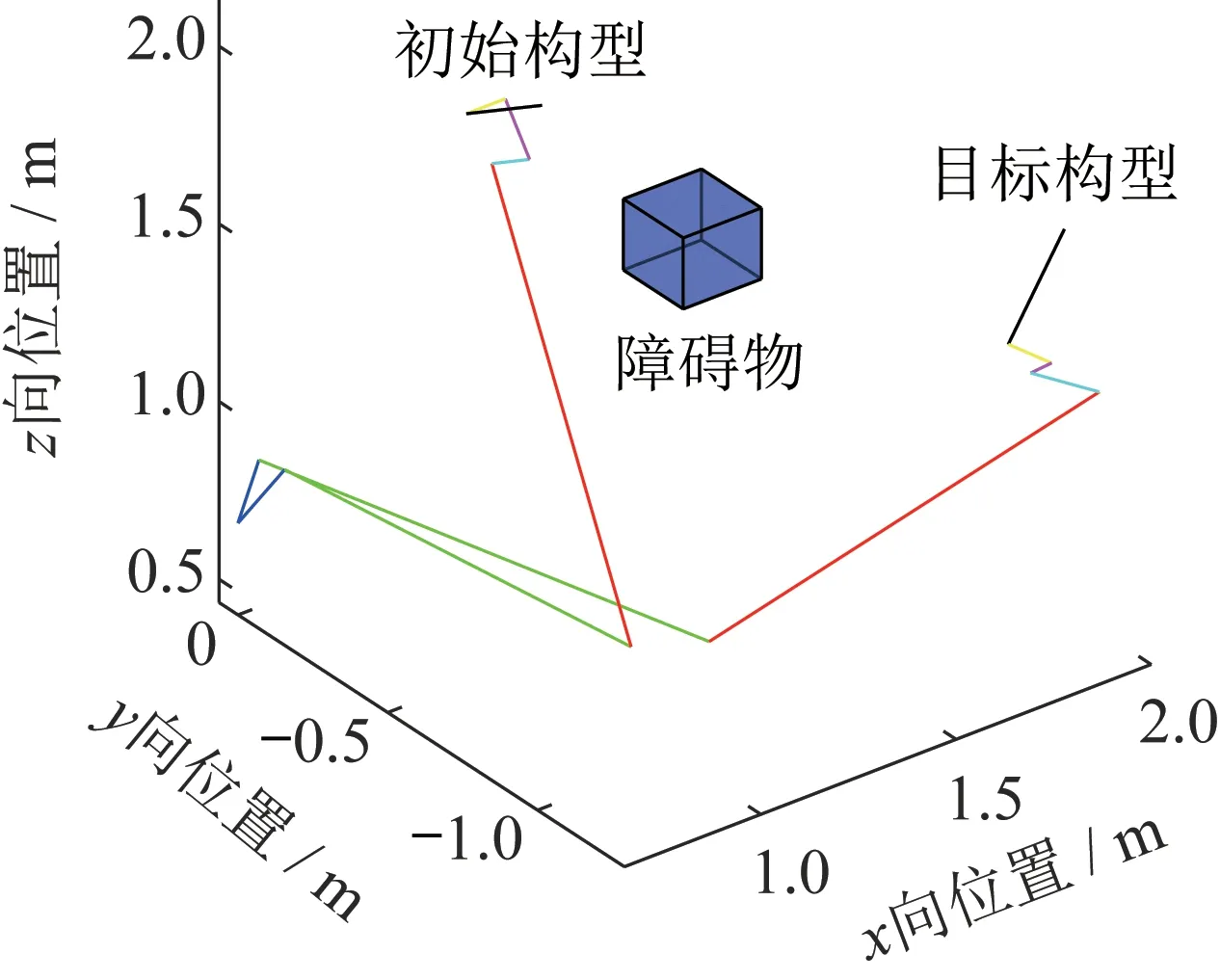
图7 初始构型和目标构型Fig.7 Schematic diagram of the initial and target configurations

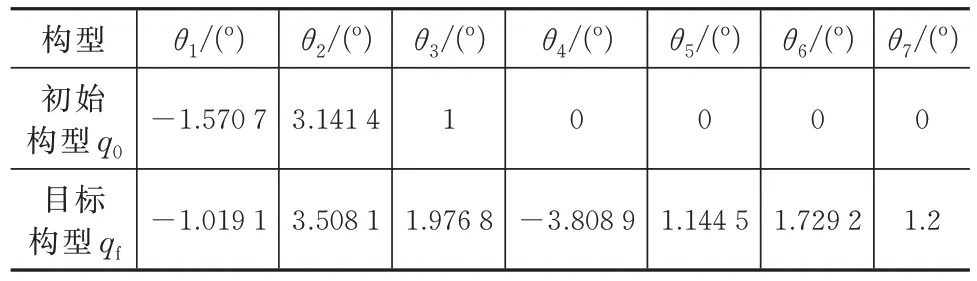
表3 初始构型和目标构型Tab.3 Initial and target configurations

可以发现，运动的前14 步没有发生调整，子运动的顺序为默认的递增顺序。之后，默认的试探路径与障碍物发生了碰撞，按算法逻辑进行了调整。最终，算法经过70 次试探，找到了一条无碰撞路径，与默认的试探路径相比，把4 个关于第3 关节角的子运动调到了路径的末尾。

路径搜索算法的三维仿真结果如图8 所示。图中可见，蓝色立方体障碍物在机械臂附近，黑色杆件模拟机械臂末端杆件，各个杆件逐渐从一个构型变化为另一构型，机械臂运动过程中，在中间2 个构型附近，最为接近障碍物，但是通过路径搜索算法的调整，并没有与障碍物发生碰撞，验证了无碰撞路径搜索算法的有效性和正确性。采用i5 处理器，当前工况下，试探性搜索算法搜索时间为19.32 s，构型空间避障算法为23.53 s，算法效率提升了17.89%。

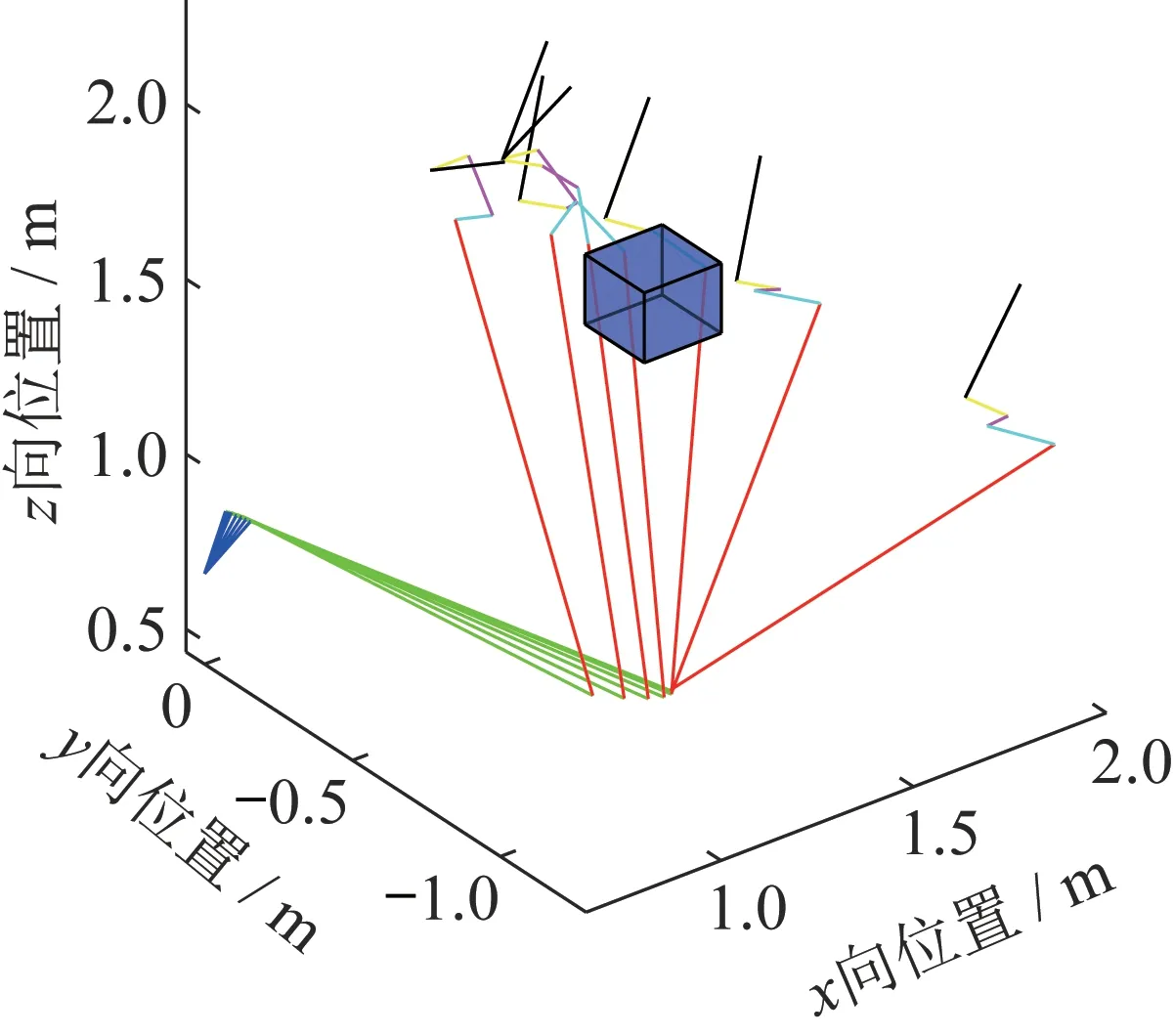
图8 路径搜索算法仿真Fig.8 Simulation of path search arithmetic

4 结束语

针对空间机械臂操作服务的需求，本文提出了一种基于构型空间的无碰撞轨迹规划算法。该算法包含了碰撞检测算法、无碰撞的目标构型求解算法、无碰撞的路径搜索算法等3 个子算法，并通过仿真算例，验证算法的有效性。与常规构型空间避障算法相比，本文提出的试探性搜索算法效率提升了17.89%。目前在已知环境下进行仿真，后续将研究考虑变结构化环境下的避障优化问题。