8吨挖掘机工作装置的有限元分析与优化设计
2022-04-27王虎奇陈志峰
王 健,王虎奇,陈志峰
(广西科技大学机械与交通工程学院,广西 柳州 545006)
1 引言
液压挖掘机作为一款重要的工程设备,对提高工程质量、加快建设进度、减轻人类劳动、缩短作业周期有着巨大的作用,因而普遍使用在国民经济的各行各业中[1]。与此同时,“节能环保”也日益成为全社会关注的焦点,用更小的消耗,产生更多的效用成为制造业追求的目标,轻量化技术因此也逐渐受到国内外制造业的重视[2]。
挖掘机轻量化设计是根据市场对节能环保产品的需求,在满足挖掘机动态运行下结构可靠性和安全性要求的同时,降低其零部件的重量。合理的轻量化设计不仅能减少用材降低企业成本,而且还能有效降低油耗减少排放,从而为市场和社会提供更有效地节能产品,因此,挖掘机轻量化也对节能减排具有非常重要的意义[3]。其中,工作装置作为挖掘的重要组成部分,其性能优劣不仅直接影响挖掘机的生产效率,还决定整机的可靠性[4]。工作装置的轻量化设计,既可以减少整机的功率损耗以及材料浪费,还可以提高挖掘机的工作效率,对挖掘机的改良开发提供了研究依据和参考。
2 工作装置的有限元分析
2.1 工作装置的简化有限元模型
挖掘机工作装置主要由动臂、斗杆、铲斗、连杆与摇杆组成,根据其工作原理及特点,可以将它进行简化设计,其简化后的几何模型,如图1所示。

图1 工作装置的几何示意图Fig.1 Geometric Diagram of Working Device
这里通过ANSYS软件自带的APDL语言来建立工作装置的模型,同时为了更好的模拟实际工作中的受力情况还建立了下车架、行走装置、旋转装置与前车架部分。
2.2 工作装置的工况选择
这里通过参考许多文献[4-8],从挖掘机的各种典型工况中选取了以下工况为研究对象。工况一:斗杆油缸全部收缩且动臂与斗杆铰接点、斗杆与铲斗铰接点以及铲尖处于同一直线位置,铲尖与停机面重合,即最大挖掘半径位置。工况二:动臂油缸全部收缩,动臂与斗杆铰接点、斗杆与铲斗铰接点以及铲尖在一条直线上并竖直向下,即最大挖掘深度位置。工况三:三个工作油缸全部收缩位置。工况四:三个工作油缸均处于最大作用力臂位置。工况五:动臂油缸全部收缩,斗杆油缸处于最大作用力臂且动臂与斗杆铰接点、斗杆与铲斗铰接点以及铲尖在一条直线上且竖直向下位置。
2.3 有限元模型的前处理
此次分析选用了高阶三维20节点固体结构单元solid186来分析工作装置的各个构件以及销轴,选用线单元link8来模拟各个工作液压缸。挖掘机工作装置结构复杂,由许多不规则的板件组成,为了节省划分网格的时间,此次分析采用自由网格的划分方式,对于连接处的耳板与销轴使用较小的尺寸来划分,对于其他部分尽可能的采用大尺寸进行划分。
2.4 载荷计算
挖掘力作为衡量液压挖掘机工作性能的一个重要参数,通常被用于校核挖掘机的使用强度,同时工作装置所产生的挖掘力又受到工作油缸的主动挖掘、非工作油缸的闭锁压力、各构件的自重及重心位置等因素的影响[10]。这里以小型挖掘机的常用挖掘方式铲斗油缸挖掘为研究对象,其中涉及到的挖掘机的详细数据,如表1所示。
在上表1中:G1表示工作装置、铲斗液压缸组与斗杆液压缸组质量的总和;D1表示动臂油缸大腔的缸径;P表示整机油缸系统压力;R1表示动臂油缸小腔的半径;D2表示斗杆油缸大腔的缸径;G2表示斗杆、连杆机构、铲斗以及铲斗液压缸组质量的总和;R2表斗杆油缸小腔的半径;D3表示铲斗油缸大腔的缸径;G3表示连杆机构与铲斗质量的总和。
2.4.1 由动臂油缸闭锁能力所决定的挖掘力
动臂油缸闭锁时的受力简图,如上图2所示。

图2 动臂油缸闭锁时的受力简图Fig.2 Diagram of Force When Arm Cylinder is Locked
在考虑挖掘力受限于动臂油缸的闭锁能力时,取整个工作装置为研究对象,根据力矩平衡对A点求矩,其计算过程如下所示:
(1)动臂油缸大腔闭锁时,闭锁压力方向由B指向C,挖掘力的计算式,如下式(1)所示。

式中:F11—动臂油缸大腔闭锁压力;W11—动臂油缸大腔闭锁压力受限下的挖掘力;d1—动臂油缸闭锁压力对A点的作用力臂;L1—G1的质心位置对A点的作用力臂;r1—挖掘力对A点的作用力臂。
(2)若W11的计算结果为负数时,则判定为动臂油缸小腔闭锁,闭锁压力方向由C指向B,其挖掘力的计算式,如式(2)所示。

式中:F12—动臂油缸小腔闭锁压力;W12—动臂油缸小腔闭锁压力受限下的挖掘力。
2.4.2 由斗杆油缸闭锁能力所决定的挖掘力
斗杆油缸闭锁时的受力简图,如图3所示。

图3 斗杆油缸闭锁时的受力简图Fig.3 Diagram of Force When Bucket Arm Cylinder is Locked
当挖掘力受限于斗杆油缸闭锁压力时,取斗杆、连杆机构与铲斗为研究对象,根据力矩平衡对D点求矩,其计算过程,如下所示。
(1)斗杆油缸大腔闭锁时,闭锁压力方向由E指向I,挖掘力的计算式,如式(3)所示。

式中:F21—斗杆油缸大腔闭锁压力;W21—斗杆油缸大腔闭锁压力受限下的挖掘力;d2—斗杆油缸闭锁压力对D点的作用力臂;L2—G2的质心位置对D点的作用力臂;r2—挖掘力对A点的作用力臂。
(2)若W21的计算结果为负数时,则判定为斗杆油缸小腔闭锁,闭锁压力方向由I指向E,其挖掘力的计算式,如式(4)所示。

式中:F22—斗杆油缸小腔闭锁压力;
W22—斗杆油缸小腔闭锁压力受限下的挖掘力。
2.4.3 由铲斗油缸主动挖掘所决定的挖掘力
铲斗油缸闭锁时的受力简图,如图4所示。

图4 铲斗油缸闭锁时的受力简图Fig.4 Diagram of Force When Bucket Cylinder is Locked
当挖掘力由铲斗油缸主动挖掘所产生时,取连杆机构与铲斗为研究对象,此时可将连杆看做为二力杆,将整体对J点求矩,其计算表达式,如式(5)所示。

式中:F3—铲斗油缸主动挖掘所产生的推力;F4—连杆对铰点O的作用力;W3—铲斗油缸主动挖掘时所产生的挖掘力;L4—F2对铰点N的作用力臂;L5—F4对铰点N的作用力臂;L6—F4对J点的作用力臂;L3—G3的质心位置对J点的作用力臂;r3—挖掘力对J点的作用力臂。
2.4.4 挖掘力计算结果
为保证整机在实际工作情况下的稳定性,挖掘力的大小通常由铲斗油缸主动挖掘时所产生的挖掘力、斗杆油缸闭锁能力受限下的挖掘力以及动臂油缸闭锁能力受限下的挖掘力中的最小值所决定,即为min(W1,W2,W3)。所计算出的详细数值,如表2所示。

表2 各个工况下产生的挖掘力Tab.2 Excavation Force Under Various Working Conditions
2.5 有限元模型的载荷添加
经过有限元模型划分网格后,通过在销轴与部件铰接处添加接触对来模拟各个部件间的旋转运动,同时采用MPC算法来减少整个分析过程的计算时间。通过整个前处理过程后,共建立了实体单元138976个,线单元3个,接触单元1656个。
结合实际工作情况,将位移约束施加在下车架底面,计算出的挖掘力均匀施加在铲尖节点的切线方向,同时添加一个重力加速度来模拟重力效果。上述工作装置的约束施加示意图,如图5所示。

图5 工作装置的约束示意图Fig.5 Constraint Diagram of Working Device
2.6 静力学分析结果
工作装置所用的材料为16MnR,可以得到许用应力为345MPa。这里应用第四强度理论作为理论依据,以材料的许用应力为判断标准,在ANAYS后处理中输出Mises等效应力[11]。在ANSYS软件中所产生的应力云图,如图6所示。
由工作装置的五种工况应力分布云图可以看出,整个机构的最大等效应力分别分布动臂上耳板与动臂的焊接处,如图6(a)所示;动臂下耳板与动臂油缸焊接处,如图6(b)、图6(c)所示;斗杆下耳板与斗杆油缸焊接处,如图6(d)、图6(e)所示;通过对比各种工况下的最大应力值,可以分析出工况四为最危险工况,其最大等效应力为316.5MPa。

图6 工作装置在五种工况下的等效应力云图Fig.6 Equivalent Stress Nephograms of the Working Device Under Five Working Conditions
3 工作装置的结构优化
3.1 优化设计的数学模型
为了减少工作装置的整体的质量,笔者选取了与重量影响关系较大的一些厚度参数为设计变量,并以工作装置材料的许用应力为约束条件,来完成工作装置轻量化的目标,详细设计的优化参数数学模型,如式(6)表示:
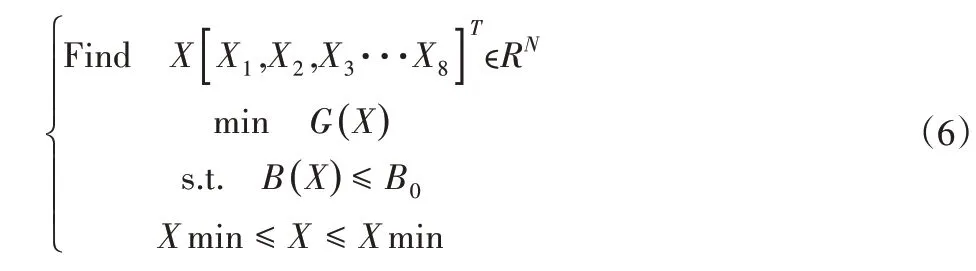
式中:X1,X2···X8—各个所设计的变量;G(x)—工作装置的重量函数;B(x)—工作装置的应力函数;B0—材料的许用应力;Xmin、Xmax—所取设计变量的最大值与最小值。
3.2 导重法优化
在实际工程中,往往需要在很短的时间内得到所需的结果,在此为了减少优化迭代的时间,这里选用了收敛速度快、迭代次数较少的结构优化导重法[12]。
3.2.1 导重法优化的敏度分析
导重法优化的准则是:最优结构应按各组构件的导重正比分配结构重量[13],为了更清楚的体现这个准则,导重法提出了敏度分析这一过程。导重法中用约束条件、目标函数与设计变量之间的导数来表示敏度,敏度的计算可以通过使用ANSYS优化工具箱中的最优梯度法(Gradient Evaluation Method)得出,最后结合敏度可以得出各个设计变量的导重与容重,他们之间的表达式,可以表示如下:

式中:Gxn—某个设计变量的导重;Hxn—某个设计变量的容重;∂B/∂Xn、∂G/∂Xn—约束条件、目标函数与设计变量之间的敏度。
3.2.2 导重法优化的迭代公式

式中:Xn(k+1)—设计变量迭代k+1次所得的值;W0—广义容重;G—总导重;ɑ—步长因子;Xn(k)—设计变量迭代k次所得的值。
3.2.3 导重法优化的迭代结果
经过6次迭代,迭代结果收敛。结合实际制造要求,对最终优化结果进行取整处理,其具体的迭代结果,如图7、表3所示。

表3 导重法迭代结果(单位:mm)Tab.3 The Iterative Results of the Guide-Weight Method

图7 工作装置重量与迭代次数的关系曲线Fig.7 Relation Curve between the Weight of Working Device and the Number of Iterations
由上图7所示:随着迭代次数的增加,工作装置的重量在逐渐下降。起初重量变化速度较快,在经历第四次迭代后重量变化速率渐渐降低,最终经过6次迭代后,结果收敛。
在上表3中:X1,X2分别表示动臂翼板及支板的厚度;X3,X4,X8分别表示斗杆侧板Ⅰ、侧板Ⅱ及盖板的厚度;X5,X6,X7分别表示铲斗底板、唇板及侧板的厚度。通过取整后的结果可以看出,工作装置的整体质量G由原来的838.6kg减少到了660kg,降重率为21.3%,同时结构的最大应力B由316.4MPa增加到了341.8MPa,虽然最大等效应力有所增加但仍满足材料的许用应力要求。
由图8的四个应力云图可以看出:经过优化设计后的工作装置最大的等效应力分别位于动臂上耳板与动臂的焊处、斗杆下耳板与斗杆油缸焊接处以及铲齿与铲斗的焊接处,整个作装置的最大应力作用在铲齿与铲斗的焊接处,其值为341.8MPa。

图8 优化设计后的应力分布云图Fig.8 Stress Distribution Nephograms After Optimized Design
4 结论
(1)分析与计算了挖掘机工作装置在五种典型工况下的挖掘力,并通过有限元软件ANSYS对处于五种典型工况下挖掘机工作装置进行静力学分析,并挑选其中最危险的工况为研究对象进行轻量化设计。分析表明工作装置在各个液压缸均处于最大作用力臂的位置将会处于最危险工况,并且最大等效应力位于斗杆下耳板与斗杆油缸焊接处。(2)基于导重法迭代原理,利用AN‐SYS中的最优梯度法进行敏度计算,再结合MATLAB软件进行反复的迭代运算。分析表明在历经6次迭代后结果收敛,工作装置多个板件的厚度都有显著的减小,整体质量在迭代的过程中逐渐减轻。(3)对优化后取整的结果再次进行有限元分析,然后将优化前后的结果进行对比。结果表明:在满足材料许用应力的条件下,工作装置轻量化设计可以达到降重率21%的效果,优化设计所得的数据可以为挖掘机工作装置优化改进提供理论依据和设计参考。
