QMB125球笼沟道磨床几何误差建模与敏感度分析

王 勇，刘 洋，朱嘉敏，金 平

（1.合肥工业大学机械工程学院，安徽 合肥 230009；2.安徽力成机械装备公司，安徽 池州 247100）

1 引言

机床的加工精度受诸多因素误差源的影响，例如几何误差，热误差，运动误差等等。其中几何误差作为机床加工精度的重要组成部分，机床的综合空间几何误差又受其各个零部件误差的影响，最后由被加工的工件上体现[1]，通过准确建立起机床的运动学模型，可以反映出零部件精度与机床整体加工精度的关系。近年来，国内外的许多研究学者在机床的精度设计方面做了相应的研究也取得了一些成果。如采用多体系统理论及拓扑结构进行机床空间误差建模[2]。但这些方法需要明确分析出所有的几何误差源且相应的计算过程较为繁琐，文献[3]通过多体系统理论及敏感度分析来识别出相应机床关键性的几何误差源，但在分析中忽略了作为几何误差源的机床组件之间垂直度的几何误差因素，针对这一现象文中以QMB125球笼沟道磨床为对象，建立起磨床整体几何误差传递模型，除机床部件几何误差外还考虑了磨床重要组件的垂直度误差，通过计算出各几何误差源的误差敏感度系数[4-5]用于指导机床精度设计。

2 QMB125球笼沟道磨床及其误差分析

2.1 QMB125球笼沟道磨床

QMB125球笼沟道磨床适用于球笼钟形壳弧球道粗精磨，其长、宽、高尺寸分别为2.20m、1.80m、2.15m。QMB124球笼沟道磨床结构，如图1所示。该磨床主要有床身，摆动回转台，主轴箱，砂轮及定位夹具组成。机床工作时，砂轮会随着主轴箱在滑台上进给到给定位置，同时摆动回转台会以固定角度来回旋转，每当加工完一个弧面，定位夹具旋转一个工位继续加工直至加工完成。

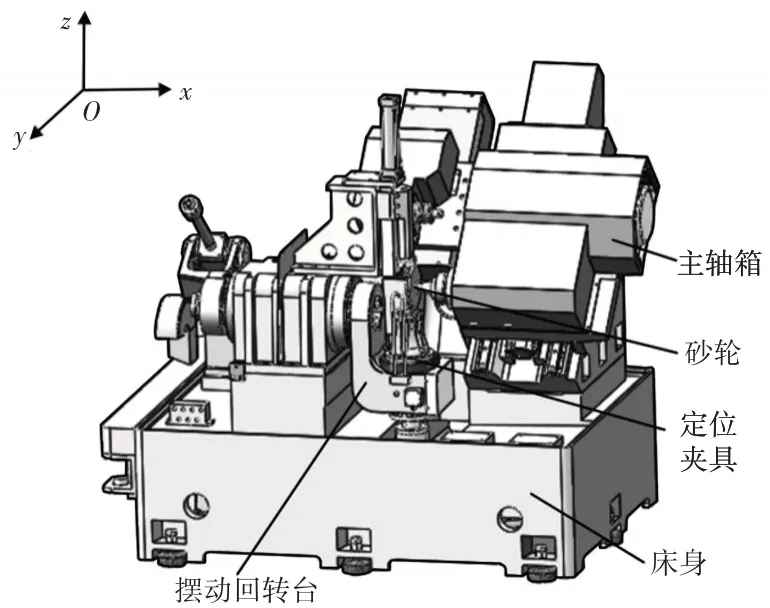
图1 QMB125球笼沟道磨床Fig.1 QMB125 Cage Cage Grinder

2.2 QMB125球笼沟道磨床组件坐标系及其误差项

构成机床的每一个零部件在其空间状态包含6个方向自由度误差，通过分析磨床的结构及其相应组件之间运动关系，总结出27项影响加工精度较大的几何误差项，其中包含3个垂直度误差项，机床各组件坐标系示意图，如图2所示。其中机床固定坐标系与床身坐标系重合，刀具坐标系，工件坐标系，主轴坐标系和进给坐标系，其中机床进给运动可以分解为沿着机床固定坐标系的坐标轴方向运动。用δ和ε分别表示位移和旋转偏差，机床主要的误差项，如图3所示。

图2 机床组件坐标系Fig.2 Machine Component Coordinate System

图3 机床主要误差项Fig.3 Machine Tool Main Error Term

3 基于多体系统理论的精度建模

3.1 多体系统理论

多体系统理论根据各组件之间的联系利用低序体阵列的方式描述出各拓扑结构，然后根据齐次坐标变换法，并结合各体之间的位姿状态精确描述出各体实际情况的位姿状态表达式[6]。

3.2 磨床拓扑结构

拓扑结构的作用即为用来描述多体系统中各体之间的关联性，在多体系统中，每一个构成拓扑结构的作为一个单元体，根据休斯顿方法特点运用低序体阵列来描述这些拓扑结构[7]。具体方法为首先选择一个单元体作为初始参考体记为0，然后以逐步远离参考体的方向依次标记每一个单元体1，2，3等等。以QMB125球笼沟道磨床建立的多体系统的拓扑结构图，如图4所示。

图4 磨床拓扑结构图Fig.4 Topology of the Grinding Machine

该多体系统存在两个分支，分别为床身到刀具（0→1→2）和床身到工件（0→3→4→5）。低序体阵列计算式为：

式中：L—低序体算子；

n—阶数；

K、S—体的序号。

当Ln(K)=S时，称S为K的n阶低序体或者K为S的n阶高序体。根据式（1）可以列出磨床的低序体阵列及相邻低序体的自由度、如表1、表2所示。

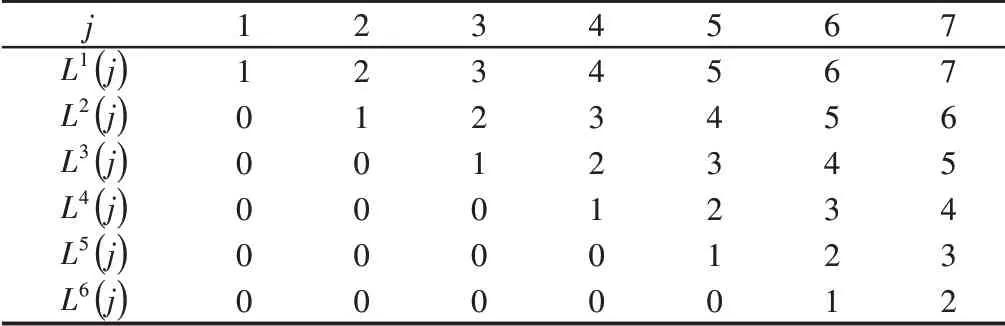
表1 QMB125球笼沟道磨床低序体阵列Tab.1 QMB125 Ball Cage Channel Grinding Machine Low-Order Body Array

表2 QMB125球笼沟道磨床相邻低序体自由度Tab.2 QMB125 Ball Cage Channel Grinding Machine Adjacent Low-Order Body Degrees of Freedom

3.3 刚体的运动特征变换矩阵

在机床结构中，任何组件的空间运动可以看成为相对参考原点的平移运动和转动运动的合成，其中刚体的运动又分为理想状态和实际状态下的运动。

当一个物体相对于另一物体在沿着x，y，z三轴方向均存在平移运动时，其坐标变换为：

上式（2）即为理想状态下的平移运动空间特征矩阵。

同样当一个物体相对于另一物体在沿着x，y，z三轴方向均存在转动运动且考虑到α，β，γ均很小时，其坐标变换为：

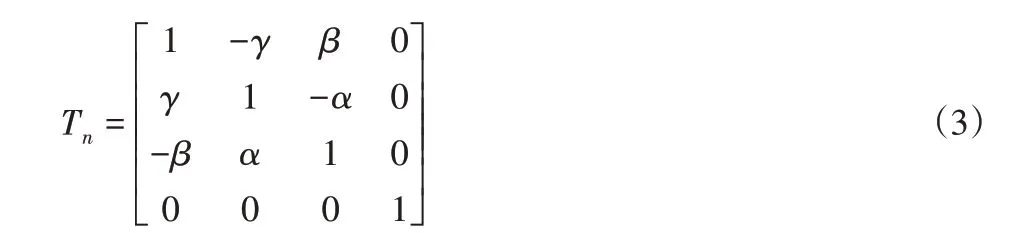
综上所述六项误差引起的综合变换矩阵为：

除此之外，考虑到加工精度的精确性，将垂直度误差项也考虑在内，机床组件在x，y，z三轴方向存在的垂直度误差可由变换矩阵如下分别表示：

式中：εxy、εxz、εyz—机床组件在x y、xz、yz三个方向存在的垂直度误差。

综上，刚体的空间状态矩阵可由相邻低序体经过空间变换矩阵来描述，即：

式中：T KS—高序体K与相邻低序体S之间空间变换矩阵；

P Ki—体K中任意一点Ki在体K中的位置坐标；

—点Ki在体S中的坐标系中的位置坐标。

空间状态变换矩阵之间可以相互传递，若Q为S的相邻低序体，两者间的空间变换矩阵为T QS，那么点Ki在体Q坐标系中的位置坐标为：

3.4 QMB125球笼沟道磨床几何误差综合建模

根据磨床的结构和各组件之间的关系从而在相邻序体间建立起空间变换矩阵，QMB125球笼沟道磨床各相邻序体之间的特征矩阵，如表3所示。

表3 QMB125球笼沟道磨床各相邻序体之间的特征矩阵Tab.3 Characteristic Matrix Between Adjacent Sequences of QMB125 Ball Cage Channel Grinder

表4中p和s分别代表静止状态特征矩阵和运动状态特征矩阵。相邻体之间实际运动特征矩阵为：

由拓扑结构图可以知道基于多体系统理论的QMB125球笼沟道磨床存在两个分支：分别是床身→砂轮分支和床身→工件分支。机床的加工精度最终由刀具成形点与工件成形点之间的相对位移来决定[8]，实际加工中，由于各种误差的存在，刀具成形点和工件成形点不可避免的存在相对位移，从而造成加工误差[9]，我们将工件成形点在其坐标系中的位置坐标设为P w=，刀具成形点在其坐标系中位置坐标设为P t=

从而QMB125球笼沟道磨床实际成形点与理想刀具成型点之间的空间综合位置误差为：

4 基于敏感度分析的误差源识别

根据QMB125球笼沟道磨床的精度模型，利用矩阵微分化的思想建立起该磨床误差敏感度分析的数学模型，根据各个误差源对空间总加工误差影响程度的不同，识别出影响加工精度较大的各个几何误差源，从而对改进机床结构，提高加工精度提供了有效理论依据。

4.1 系统敏感度模型的建立方法

目前在工程计算领域系统敏感度模型的确定使用最多还是敏感度函数法，其具体方法为用变量表示系统的性能参数，用变量表示系统的结构参数化，y与a存在如下关系

当参数取初值a0，y的值记为y0，当参数变化为a i=a0i+Δa i时，相应的系统性能参数变为：

则由于参数变化而造成的系统误差为：

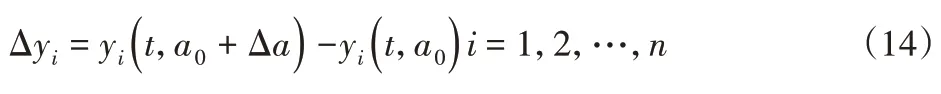
假设在a的初值a0处，y i对存在k阶偏导数，利用多变量函数微分法及泰勒公式同时省去余项可得：

实际情况中，由于高阶导数的求解比较复杂，适用性不高，故多采用一阶敏感度函数分析，上式中k取1时所得到的一阶偏导数即为一阶敏感度函数，若F(x)可导，则F(x)的一阶敏感度函数表达式为：

机床空间总误差E与各几何误差项Δe i的一阶敏感度函数为：

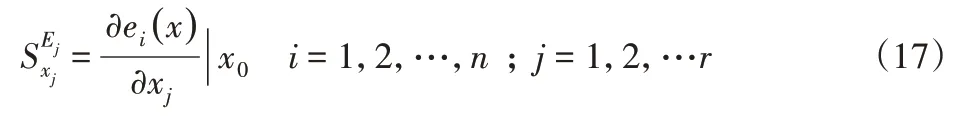
根据式（17）可以建立起一般的机床误差数学模型，该模型可以显性的表示为：

式中：L—所有几何误差项构成的误差矢量；

P w—被加工件在其坐标系中的矢量；

U—机床各运动轴间位置矢量；

U w—工件位置矢量；

U t—刀具位置矢量。

根据式（18）可知F为连续可微函数，将其按一阶泰勒级数展开并省略其高阶项可得：

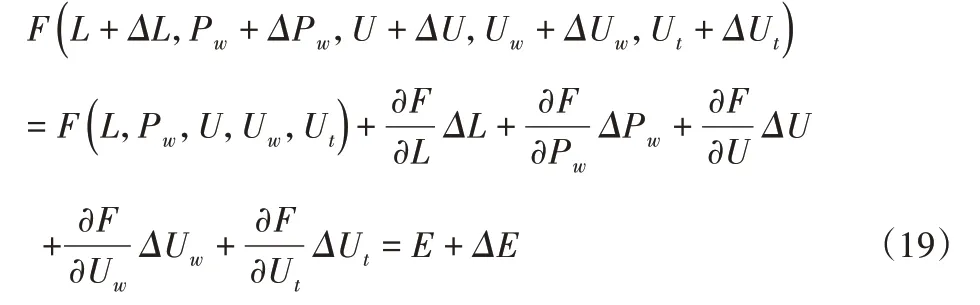
其中由于上式中的P w，U，U w，U t在实际分析中均可设为定值，固只考虑几何误差部分上式可简化为：

因此可得出机床误差敏感度模型为：

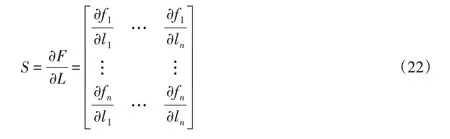
4.2 QMB125球笼沟道磨床误差项敏感度分析

机床的加工精度由其零部件各项几何误差的空间耦合而成，而各项几何误差对加工精度的影响程度不同，需要对其进行敏感度分析，从而找出相对加工精度影响较大的几何误差项。

针对这里分析的QMB125球笼沟道磨床，考虑到其各部分组件相对运动关系得到共27项几何误差项。根据上式（22）可以定义出机床空间总误差E对机床各个几何误差项Δe i的一阶偏导数绝对值为该磨床加工中心的误差敏感度：

以εx01为例，求解其误差敏感度有：

具体的实验数据可以通过双频激光干涉仪器测量得到，双频激光干涉仪是通过计算频率差的变化值来测量位移[10]，因其适应外界环境因素较强，故可通过双频激光干涉仪测量该机床的直线误差，旋转误差，垂直度误差得到实验数据，具体测量方法，如图5所示。直线度误差δx01、δy01、δz01等直线度误差通过激光干涉仪在相应的轴段上直接测量得到；旋转误差可以通过6条直线的定位误差和直线运动误差继而联系方程组求解［11］。

图5 旋转误差的测量Fig.5 Measurement of Rotation Error

将测端分别在y=0、z=0；y=y0；z=0、y=0、z=z0三处直线沿1，2，3运动。测量直线上各点的直线度误差，则直线度误差δx01、δy01、δz01和旋转误差εx01、εy01、εz01存在以下关系：

因此可以联立方程组求解相应的各个旋转误差项；利用对角线法测量垂直度误差，如图6所示。

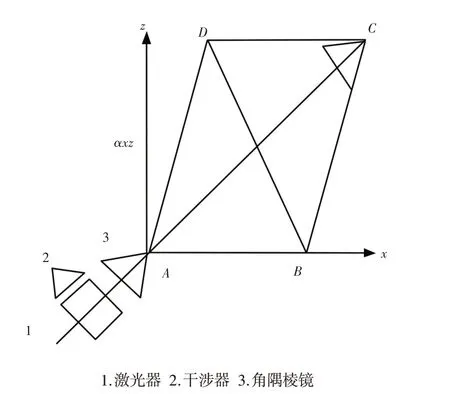
图6 垂直度误差的测量Fig.6 Measurement of the Verticality Error

控制滑座先后沿着AC，BD运动，l1和l2设为两条对角线的长度，滑座在沿着两条对角线运动时，在x，y方向的行程记为D x，D z，则在沿着两条对角线运动时的位移差[12]为：

因而垂直度误差：

通过实验测量误差数据，角误差和线误差结果在0.01左右，垂直度误差在0.005°左右，考虑到机床允许几何误差值范围不超过0.015，在满足机床加工精度需求的前提下在下述计算中统一取磨床6方向自由度误差值为0.01，三方向垂直度误差值为0.005°。

分别将27项几何误差代入上式中计算得到x，y，z三方向敏感度分析情况，如表4、图7～图9所示。

图7 E x方向上敏感度系数Fig.7 Sensitivity Coefficient in the Direction of E x

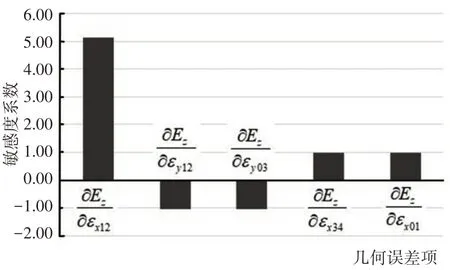
图9 E z方向上敏感度系数Fig.9 Sensitivity Coefficient in the Direction of E z

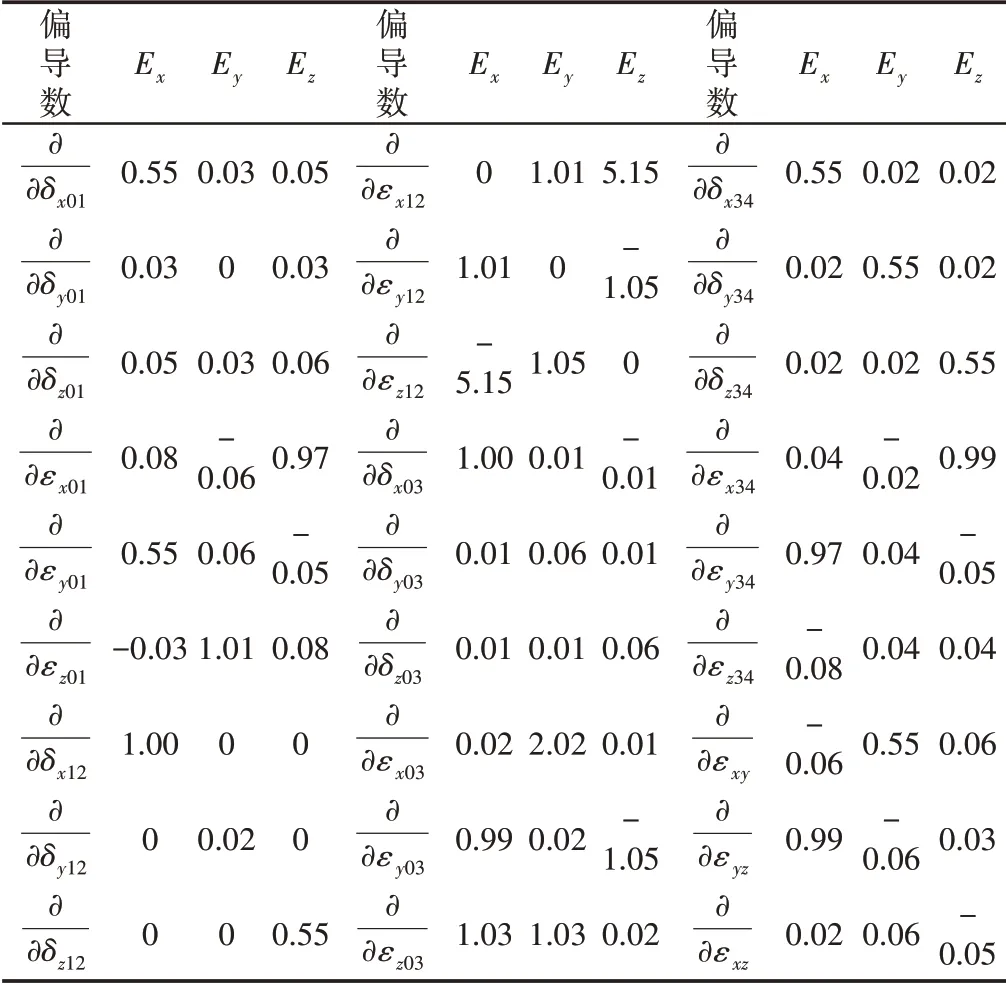
表4 QMB125几何误差源敏感度分析表Tab.4 Sensitivity Analysis Table of QMB125 Geometric Error Source

由上图6～图8分析可得出如下结论：

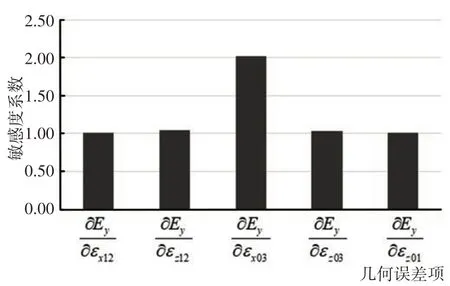
图8 E y方向上敏感度系数Fig.8 Sensitivity Coefficient in the Direction of E y

磨床加工的主要相对位置误差主要存在于：

（1）床身与摆动回转台之间，并且敏感度系数较大的是在绕z轴的相对角位移误差。为减小该项误差，可在机床设计时着重提高床身与摆动回转台之间的连接稳定性，避免其在z方向上的旋转摆动影响加工误差。

（2）砂轮与主轴箱之间，并且敏感度系数较大的是在绕x轴的相对角位移误差。为减小该项误差，可在机床设计中着重优化主轴箱与刀具间的紧固装置，避免其在加工中由于砂轮的x方向旋转振动影响加工误差。

5 结论

几何误差建模与敏感度分析是机床精度设计中的核心内容之一，QMB125数控磨床为研究对象，基于多体系统理论，通过低序体阵列来描述磨床的拓扑结构，建立起机床的运动学模型，对磨床的27项几何误差源进行误差取样，同时利用矩阵微分法通过计算与分析误差敏感度系数，对影响加工精度因素的重要度进行筛选，从而有效识别出磨床关键性几何误差源，为合理经济的提高机床精度设计提供理论参考。