基于M-P法的抗滑桩支护边坡稳定性研究

2022-04-27席新林姬云平

能源与环保 2022年4期

席新林，姬云平，李明

(中铁第一勘察设计院集团有限公司，甘肃兰州 730000)

抗滑桩加固策略是边坡支护中充分结合支挡防护的方式，工程中的实际应用可分为2种情况：设计和验算。设计是指规定边坡要达到一定的安全系数，求得抗滑桩受到的下滑力，从而确定桩距、桩径、桩长和配筋；验算是指从抗滑桩桩径和配筋等反向抗滑桩可提供的抗力，求得边坡的安全系数，评价边坡的稳定性。

现有的抗滑桩下滑力分析方法主要有以下3种：不平衡推力法[1]、极限分析法[2-3]和有限元方法[4-6]。不平衡推力法计算过程简单，应用广泛，但其需要确定一个已知的滑动面，并且力学推导不严谨，计算精度不高。极限分析法能够考虑土体的绕流和土拱效应问题，但实质上求得的作用力是土压力，多数情况下比不平衡推力法求得的下滑力小，设计时为保险起见，往往取两者的较大值。有限元方法能反映边坡的应力场和位移场，但其中涉及材料屈服准则的选用、失稳判据的确定等诸多复杂因素，而这些因素的确定尚无统一的标准，使得一线工程技术人员多难以掌握和应用。对于边坡由于内外部条件发生变化而需要验算其稳定性的情况，李家平等[7]基于瑞典法和简化Bishop法，采用圆弧滑动面分析抗滑桩支护后临水岸坡的稳定性，但国内外大量的工程实例表明，边坡的滑动面实际是非圆弧状的。文献[8]采用有限元方法，分析了水位波动条件下抗滑桩抗滑稳定性，采用的是指定软弱滑动面。目前，被列入各行业规范的边坡稳定性方法仍然以极限平衡法为主，其中最为严格满足力和力矩平衡条件的应属Morgenstern-Price(M-P)法[9-10]，文献[11-13]分别得到了M-P法的积分形式和代数迭代形式。文献[14]指出，改进的M-P法可以考虑抗滑桩的支护作用，但未明确抗滑桩作用力的方向和作用点，亦未说明如何考虑抗滑桩布设后滑动面位置的确定，其适用性仍有待进一步提高。

综上所述可知，比较理想的抗滑桩支护边坡分析方法应该具有以下3个方面的特点：①推导过程条理清晰、力学概念明确，有较好的计算精度；②能分别从设计和验算2个方面考虑，易于工程应用；③滑动面可以是确定的软弱滑动面，也可以是搜索得到的非圆弧最危险滑动面。而这几个方面正是本文研究的出发点与核心内容。

本文拟在改进的M-P法基础上，建立可分别考虑设计和验算2种情况的抗滑桩支护边坡稳定性分析模型，并通过引入自适应遗传算法，实现最危险滑动面的自动搜索，以期不断完善抗滑桩支护边坡的稳定性分析方法。

1 考虑抗滑桩支护作用的M-P法

1.1 模型建立

边坡及滑体如图1所示，边坡的坡面和滑动面可以是任意形状，同时考虑地下水的作用影响。将边坡滑体划分成n个竖直条块，将其条块i取为隔离体并进行受力分析(图2)，则条块i上的作用力有(当i为0和n时，代表第1条块的初始状态量和第n条块的最终状态量)：块自重Wi；②条块水平地震力KcWi，Kc为水平地震惯性力影响系数；③条块作用于坡面的外力Qi，与竖直方向的夹角为i；④条块底面水压力的合力Ui；⑤条块底面法向反力Ni和抗力Si；⑥条块竖直方向条间力Xi1、Xi，水平条间力Ei1、Ei，水平条间力的作用点与滑动面的垂距分别为zi1、zi；⑦条块抗滑桩的作用力Pi，在设计时指抗滑桩所受到的下滑力，验算时指抗滑桩可提供的抗力，其方向与条块底面平行，作用点高度Hpi可取条块高度的1/2～1/3，本文的计算分析统一取1/3。

图1 边坡及滑体示意Fig.1 Schematic diagram of slope and sliding body

图2 边坡及滑体的受力分析Fig.2 Mechanical analysis of slope and sliding mass

1.2 抗滑桩桩后下滑力的确定

由第i条块底面法线方向上力的平衡，得：

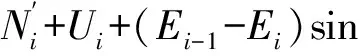
(1)

由第i条块底面切线方向上力的平衡，得：

(Ei-1-Ei)cosαi-(Xi-1-Xi)sinαi-Si-Pi+wi(sinαi+kccosαi)+Qicos(αi-δi)=0

(2)

由第i条块底面中点的力矩平衡，得：

(3)

条块底面的抗力Si由岩土体的黏聚力和内摩擦角提供，可由摩尔—库仑强度准则得出极限状态下的抗力，再根据强度折减法原理进行折减，即：

(4)

式中，c′、φ′分别为i条块底面有效黏聚力和内摩擦角；Fs为边坡安全系数，由规范或设计人员确定。

各条块之间的条间力E和X符合以下关系：

Xi-1=λki-1Ei-1

(5)

Xi=λkiEi

(6)

式中，λ为比例常数；ki、ki-1分别为条间力函数，可采用ki=ki-1=1(Spencer法)或半正弦函数。

根据第i条块的力平衡条件，将式(4)、式(2)、式(1)、式(5)联立，可得水平条间力E的表达式为：

ψiEi=ηi-1ψi-1Ei-1+Fs(Ti+Pi)-Ri

(7)

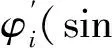
假设仅在边坡第m条块处设计一排抗滑桩，由边界条件可得E0=0，En=0，则式(6)可化为：

(8)

式(8)即为桩后下滑力的表达式，但其中隐含这一未知参数，故须采用迭代的方法求解。定义条间力矩M为水平条间力E与垂距z的乘积，即：

Mi-1=Ei-1zi-1

(9)

Mi=Eizi

(10)

由式(3)、式(8)可得条间力矩M的表达式为：

Mi=Mi-1+Ei-1bi(tanαi-λki-1)/2+Eibi(tanαi-λki)/2+kcwihi/2-Qihisinδi-Pihicosαi/2

(11)

由边界条件可得M0=0，Mn= 0，式(9)可化为：

(12)

计算时，可先假定初值P0和λ0，代入式(7)和式(10)中，计算得出P和λ。若ΔP和Δλ>ε(ε为一个足够小的数，如0.001)，则将最近一次计算得出的P和λ再进行迭代，直到ΔP和Δλ<ε。

1.3 抗滑桩支护边坡安全系数的确定

若边坡已经设置抗滑桩，由于边坡内外部条件变化而需要重新确定边坡的安全系数，可将式(7)作简单变形，即可得到抗滑桩支护边坡的安全系数表达式：

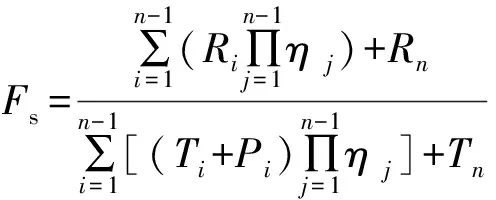
(13)

此时有抗滑桩作用的条块将其作用力Pi作为已知量，而未有抗滑桩作用的条块Pi=0。同样可用迭代方法将式(7)和式(11)联合求解。文献[13]的方法表明，滑动面选取较为合理，迭代不超过10次即可得到Fs和λ的收敛值。

至此，已建立出可分别考虑设计和验算2种情况的抗滑桩支护边坡分析模型，下面将探讨如何实现边坡最危险滑动面的智能搜索。

2 边坡非圆弧滑动面搜索

2.1 自适应遗传算法

众多学者将遗传算法引入到边坡最危险滑动面的搜索中，取得了很好的效果。文献[15-16]针对基本遗传算法中交叉概率和变异概率取值常有凭人为经验的缺点，提出了自适应遗传算法。其核心内容是算法中的交叉概率和变异概率能根据适应度自行调整，当遗传种群中的各个体适应度变化较小时，交叉概率和变异概率增加，反之则减少。两者的具体适应调整计算公式为：

(14)

(15)

式中，f为将要交叉个体中的适应度较大值；f*为将要变异个体中的适应度值；fmax为群体中的最大适应值；favg为群体的适应度平均值；Pc1、Pc2为交叉概率上、下限；Pm1、Pm2为变异概率上、下限。

2.2 边坡任意滑动面的构建

边坡每一个可能的滑动面对应一个下滑力P或安全系数Fs，因此，可建立如下的边坡安全系数求解优化计算模型：

(16)

式中，P(X)和F(X)分别为抗滑桩作用力和边坡安全的表达式；X=[x1，x2，…，xn]为与安全系数对应的滑动面控制变量；Ω为可行域。

本文构建的滑动面是非圆弧滑动面，首先将其离散化，然后通过确定控制点的坐标位置，采取以直代曲的方法来实现任意滑动面的构建(图3)。滑动面AB上任一点i的坐标(xi，yi)由式(17)确定：

(17)

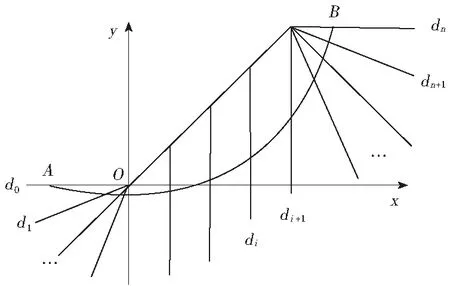
图3 滑动面搜索模式示意Fig.3 Schematic diagram of sliding surface search mode

至此，已建立出完整的抗滑桩支护边坡分析方法，整个分析方法的流程如图4所示。由前述可知，该分析方法是建立在改进M-P法基础上，属于极限平衡范畴，便于工程人员理解和掌握；同时，该方法能从设计和验算2方面入手，适合工程实际的不同要求；此外，它还可以考虑抗滑桩支护边坡的非圆弧最危险滑动面。

3 算例验证与讨论

3.1 算例验证

采用文献[2]中的算例，边坡尺寸和材料参数如图5所示。首先从验算角度出发，对未支护边坡比较本文方法与其他方法的结果。

各种方法及其对应的安全系数见表1，各种方法的滑动面位置如图6所示。本文所得的安全系数为1.08，是各种方法结果的最小值，在坡脚处滑动面位置与其他方法有一定差别，这是由于本文采用的是非圆弧滑动面，能得出更为复杂的滑动面和与之相对应安全系数的结果。然后再从设计角度出发，比较抗滑桩的受力情况。令边坡的安全系数为Fs=1.5，在距离坡脚s=13.7 m 处设置抗滑桩，对应的下滑力P= 522 kN。

图4 抗滑桩支护边坡稳定性分析流程Fig.4 Flowchart for analysis of slope stability supported by anti-slide piles

图5 边坡算例示意Fig.5 Schematic diagram of slope calculation example

表1 不同方法计算的未支护边坡安全系数Tab.1 Safety factor of unsupported slope calculated by different methods

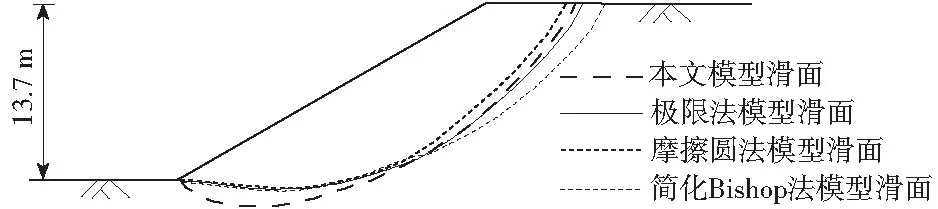
图6 不同方法得到的滑动面位置Fig.6 Sliding surface position obtained by different methods

3.2 抗滑桩设计

在距坡脚2.5～22.5 m内，每隔2.5 m布置一排抗滑桩，要求达到的安全系数为1.2～1.5，计算结果如图7所示。由图7可知，当要求达到一定的安全系数Fs时，不同位置的抗滑桩所需提供的抗力大小基本不变。而对于抗滑桩设置的位置，则根据安全系数的大小有所区别。若抗滑桩过于靠近坡脚或坡顶，边坡就无法达到一个较高的安全系数。表现为即使抗滑桩能够提供足够大的抗力，但最危险滑动面已不再穿过抗滑桩，而是要么位于抗滑桩与坡顶之间，要么位于抗滑桩与坡脚之间。本文对不穿过抗滑桩的滑动面统称为“次生滑动面”。因此，图7中才会出现要达到的安全系数越高，适合布桩的范围越窄的情况。

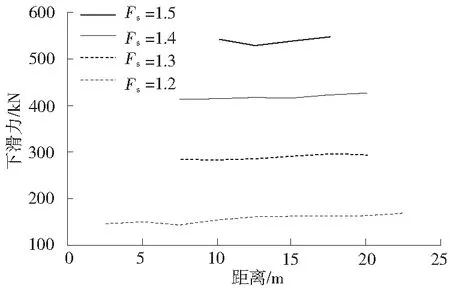
图7 不同安全系数下桩位和下滑力的关系Fig.7 Relationship between pile position and sliding force under different safety factors

3.3 边坡安全系数验算

在距坡脚2.5～22.5 m内，每隔2.5 m设置一排抗滑桩，假设抗滑桩位能够提供的抗力已知，为100～800 kN，计算边坡的最小安全系数，所得结果如图8所示。从图8可知，在坡脚和坡顶附近，边坡最危险滑动面极容易出现不穿过抗滑桩的情况，边坡安全系数由次生滑动面控制。在坡顶或坡脚设置抗滑桩，边坡安全系数随着抗滑桩抗力的增大先是增大、然后增长趋缓直到不再增长。而设置在边坡中部的抗滑桩，边坡安全系数随着抗滑桩抗力的增大而增大，基本呈线性关系。