基于不同排布型式的弧形抗滑桩边坡加固效果研究
2022-04-27陈雪亮
黄 延,陈雪亮
(1.杭州市城乡建设设计院股份有限公司,浙江 杭州 310000; 2.杭州临平基础设施建设有限公司,浙江 杭州 310000)
近年来,由于地震频发,我国西南山区经常出现规模的山体滑坡现象[1-2]。现有边坡加固措施建设速度慢,投资成本大,稳定性差,实际加固效果不理想。因此,有关学者对新型的抗滑结构加固边坡的形式投入了大量研究。文献[3]以某实际工程为背景,采用数值模拟和调研的方式,对框架式微型桩加固边坡的效果进行详细研究,同多排式加固桩措施进行比较,其桩身位移和弯矩均明显减小,满足相关设计要求;文献[4]通过分析在岩土边坡工程中的原理、失稳判定、强度准则等,选用合适的抗滑支挡结构可解决多类型滑坡问题;文献[5]通过讨论传统悬臂式和锚索式抗滑桩的优劣性,以大量实际工程资料为基础,提出了弧形间隔排桩+桩顶连系的抗滑结构模型,充分证明了这种新型支挡结构在加固边坡方面的优越性;文献[6]基于传统悬臂式抗滑桩的缺点,利用弧形布置的抗滑桩方式,且桩顶采用连系梁连接来共同受力,推导了这种组合式支挡结构的内力及位移,其结果表明弧形排列的支挡结构能有效的约束桩身的整体位移,能充分发挥将连系梁结构的抗压优势;文献[7]探讨了不同形式抗滑桩结构,讨论并研究了这些结构在设计计算时的关键问题和适用条件,结合工程实际给出了设计方法。往期大多学者对于抗滑桩的研究重点集中在理论推导、桩自身的力学参数和桩长等方面对横向和竖向承载能力的评估[8-9],以及在群桩的不同布置下对于边坡整体稳定等方面的研究[10-12],而对新型的抗滑结构形式的研究较少。
基于以上研究,本文基于弧形桩顶连系梁抗滑桩的基础之上开展抗滑桩加固边坡的改进形式研究,并对不同型式下的抗滑结构进行参数适应性分析,通过仿真结果为有关设计和工程应用提供合理参考。
1 理论分析
1.1 弧形桩顶连系梁抗滑结构理论分析
对于弧形布置跨距为L的连系梁抗滑结构的计算模型如图1所示,该计算模型为两铰拱模型,基本体系中共有n个未知力,其中X1为右端拱铰处沿水平x轴负向的水平力,Xi为连系梁上沿法向的集中力(i取偶数,i=2,4,…,n-1),Xj为连系梁上沿轴向的集中力(j取奇数,j=3,5,7,…,n)。

图1 弧形布置连系梁计算模型Fig.1 Calculation model of arc row piles with arc coupling beam on pile top
通过对计算模型施加上述单位未知力,通过叠加计算可得作用单位多余未知力的两铰拱的结构位移,即:
(1)
(2)
(3)
(4)
(5)
(6)
式中,δij为基本结构在单位未知力Xj单独作用沿Xi方向的位移(i为法向,j为轴向);Mi、Qi和Ni分别为基本结构在单位未知力Xi作用产生的弯矩、剪力和轴力;k为截面形状系数,圆形截面取10/9;E为结构弹性模量;I为截面惯性矩;A为截面面积;G为剪切模量;ds为连系梁的单位微分长度。
1.2 边坡安全性分析
基于有限元强度折减分析法来对边坡的稳定性进行分析[13],在假定边坡整体所受外力荷载不变的情况下,通过将边坡岩土体的参数黏聚力c和内摩擦角φ同时除以一个折减系数Ft,从而获得折减之后的ct和φt,并将所得参数进行稳定性迭代求解运算。当边坡处于极限平衡状态时,折减系数Ft即为边坡的安全系数:
φt=arctan(tanφ/Ft)
(7)
ct=c/Ft
(8)
2 工程简述
该露天边坡位于西南地区某县境内,邻近特大铁路桥梁,所在岩堆大致呈扇形分布,岩堆体坡面较陡,坡度为38°~45°,该区域地形是我国起伏较为剧烈的深切陡峭的高山峡谷。该边坡地层岩性分布较为复杂,在该区域穿越4条地震带,有频繁地震活动。滑坡体主要为含角砾低液限黏土和块石土,滑坡体内裂隙发育,在天然降雨和地震作用下也容易引起滑坡,可能会对下部特大桥梁和列车的运行造成威胁。介于该边坡地理位置特殊,需对其进行整治加固,拟采用弧形布置的连系梁抗滑桩支挡结构对该边坡进行加固,并讨论不同形式支挡结构的加固效果。
3 建模分析
3.1 数值模型
采用有限元软件建立边坡三维模型,如图2所示。该模型长×宽×高=40.0 m×15.5 m×22.0 m,边坡土层从上到下分别为含角砾低液限黏土、块石土和粉砂质泥岩。弧形布置连系梁抗滑桩布置在距离模型底部16.8 m的坡面上,抗滑桩直径为0.4 m,长度为8.0 m,沿弧形等间距分布,连系梁弧长设为15.0 m,宽度为0.6 m,厚度为0.4 m。两端部设置为拱脚抗滑桩,为正方形截面,宽度设定为1.0 m,桩长设为8.0 m,矢跨比设为0.14。

图2 边坡三维模型Fig.2 Three-dimensional model of slope
3.2 参数选取
设定露天边坡岩土体本构模型采用摩尔—库仑模型,连系梁和拱脚抗滑桩采用的是钢筋混凝土。抗滑桩的材料参数的选取是直接影响边坡稳定的决定性因素,根据实际工程现场探测取样、试验,结合现场边坡的地质情况及施工经验,选取相应符合工程的岩土体和抗滑桩的材料力学参数见表1。
3.3 接触约束
岩土体、连系梁和抗滑桩等均采用三维实体单元,桩和土之间的摩擦接触采用的是摩尔—库仑准则,连系梁与抗滑桩顶端的连接为刚性连接。整体模型仅考虑在自重应力场下的作用,边界条件采用左右(X方向)、前后(Y方向)、底部(X,Y,Z方向)约束,如图3所示。
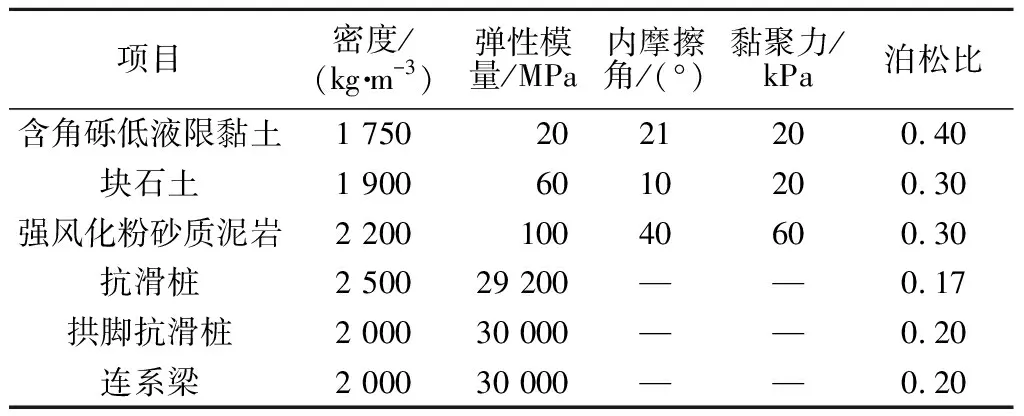
表1 岩土体和抗滑桩参数Tab.1 Parameters of geotechnical and anti-slide pile

图3 约束边界Fig.3 Bound boundary
4 结果分析
4.1 边坡安全系数分析
边坡安全系数:天然边坡0.925;直线布置(8根)1.248;弧形(反向)布置(8根)1.091;弧形布置(8根)1.315;弧形布置(6根)1.215;弧形布置(4根)1.103。自然边坡安全系数小于1,处于不稳定状态,在受到外部条件的影响,极易引发滑坡。通过设置抗滑桩,能使边坡趋向于稳定状态,但不同形式抗滑桩下的边坡安全系数不同。弧形和直线布置的安全系数要大于弧形布置(反向),弧形布置(8根)安全系数最高,随着桩数的减少,安全系数逐渐降低。
4.2 边坡整体位移分析
边坡在不同型式抗滑桩下的整体位移云图如图4所示。
(1)通过自然边坡和不同型式抗滑桩下的边坡位移对比可知,不同型式抗滑桩对边坡都具有一定的加固效果,能有效阻止抗滑桩后方土体滑动面的形成,保证边坡稳定。

图4 不同型式抗滑桩下的整体边坡位移Fig.4 Displacement of integral slope under different types of anti-slide piles
(2)通过对比相同桩数(8根)下抗滑桩的加固效果可知,采用弧形布置(8根)的边坡位移 (0.27 m)小于直线布置(8根)的位移(0.42 m),这是由于弧形连系梁较直梁起到了一个承压的作用。
而弧形(反向)布置抗滑桩的边坡位移(0.48 m)要大于直线布置抗滑桩的位移(0.42 m),说明弧形(反向布置)抗滑桩在限制边坡滑移方面的效果并不明显,因此,对相同桩数(8根)下的抗滑桩的加固效果进行比较可知,弧形布置抗滑桩加固效果最好,直线布置抗滑桩次之,弧形(反向)最小。
4.3 边坡塑性区分布
边坡在不同型式抗滑桩下的边坡塑性区如图5所示。

图5 不同型式抗滑桩下的边坡塑性区Fig.5 Plastic zone of slope under different types of anti-slide piles
(1)同自然边坡对比,抗滑桩能有效减少边坡塑性区的发展,能将边坡塑性区限制在一定范围之内,降低出现滑坡的风险。
(2)通过与相同抗滑桩数(8根)下的塑性区对比,三者塑性区面积大小依次为:直线布置>弧形(反向)布置>弧形布置,通过对比可以发现,弧形布置抗滑桩较直线布置区域要大,且更靠近坡角位置。能有效减小边坡塑性区面积,为了边坡安全考虑,建议抗滑桩布置尽量靠近坡角位置。而从最大剪切应变增量数值上来看,弧形(反向)布置(0.46 m)>直线布置(0.30 m)>弧形布置(0.21 m),反映出弧形布置抗滑桩在空间上的分布较前两者能有效减小边坡剪切应变增量。
4.4 抗滑桩位移分析
不同型式抗滑桩下的桩体位移如图6所示。从图6中可知,各个抗滑桩在边坡滑移作用下出现了不同程度的变形,且最大位移与变形状态有关。直线型布置的抗滑桩最大位移出现在连系梁顶部,为2.75 mm。弧形(反向)布置抗滑桩桩身所受压力较大,最大位移出现在连系梁下部桩体(图6(b)),最大位移为3.30 mm。弧形布置(4、6、8根)抗滑桩的最大位移均出现在连系梁底部位置,分别为5.23、3.60和3.02 mm。提取连系梁中部抗滑桩沿深度的位移数据,绘制不同型式中部抗滑桩沿桩深的位移(图7)。由图7可知,不同型式抗滑桩的位移都随着深度的增加而逐渐减小,仅弧形(反向)抗滑桩在桩深为1.75 m出现最大位移。各抗滑桩在桩深达到6.0 m时,抗滑桩位移基本趋于稳定。弧形(4根)抗滑桩的整体位移均远大于其他抗滑桩,说明其加固边坡的效果小于其他形式抗滑桩。
4.5 连系梁位移分析
不同型式抗滑桩下的连系梁水平位移云图如图8所示。为分析连系梁在边坡滑移作用下的位移情况,分别在连系梁顶部从左到右等间距布置10个监测点,并将提取的数据绘制(图9)。
从图9中可知,各种型式连系梁的位移都大致呈现弧形分布,最大位移出现在梁中部附近。通过对比相同桩数(8根)连系梁的位移可知,由于直杆分布的连系梁距坡脚有一定的距离,故整体位移偏小,其最大位移仅为2.4 mm。弧形(反向)布置的抗滑桩限制边坡滑移的作用没有直线布置抗滑桩明显,其连系梁最大位移较直线布置连系梁大,为3.12 mm。

图6 不同型式抗滑桩下的桩体位移Fig.6 Pile displacement under different types of anti-slide piles

图7 不同型式中部抗滑桩沿桩深的位移Fig.7 Displacement of anti-slide piles along pile depth with different types
弧形布置抗滑桩的中部桩基离坡脚较近,承受压力较大,故其连系梁在中部位置处的位移较大,为2.81 mm。通过对比不同桩数(4、6、8根)抗滑桩的连系梁的位移可知,弧形布置(4根)抗滑桩的连系梁的全梁位移要远大于弧形布置(6、8根)抗滑桩所对应的连系梁的位移,说明前者限制边坡滑移的作用明显削弱。弧形布置(6根)与(8根)连系梁的全梁位移分布较为近似,前者仅在梁中部位置附近的位移较后者略大,说明二者抗滑桩支挡结构整体受力较为稳定,对边坡加固效果显著。

图8 不同型式抗滑桩下的连系梁水平位移云图Fig.8 Nephogram of coupling beam displacement under different types of anti-slide Piles
4.6 弧形连系梁抗滑结构优化分析
进一步对弧形连系梁抗滑结构进行优化分析,选取弧形布置(8根)连系梁抗滑结构在不同混凝土等级、连系梁矢跨比以及抗滑桩长度的情况下的边坡,通过计算并统计得到边坡安全性系数见表2。从表2中可知,随着弧形连系梁抗滑结构混凝土等级的增大,边坡的安全系数逐渐增大,但混凝土等级达到一定程度后,增加的趋势逐渐变缓,对边坡的加固作用减弱。通过不同连系梁矢跨比对比,随着矢跨比的增加,边坡的安全系数逐渐增大,说明增大连系梁的矢跨比能有效对边坡进行加固。对于不同抗滑桩长度而言,一定范围内增加抗滑桩的长度能有效地限制边坡滑移。

图9不同型式抗滑桩下的连系梁水平位移Fig.9 Diagram of coupling beam displacement under different types of anti-slide Piles
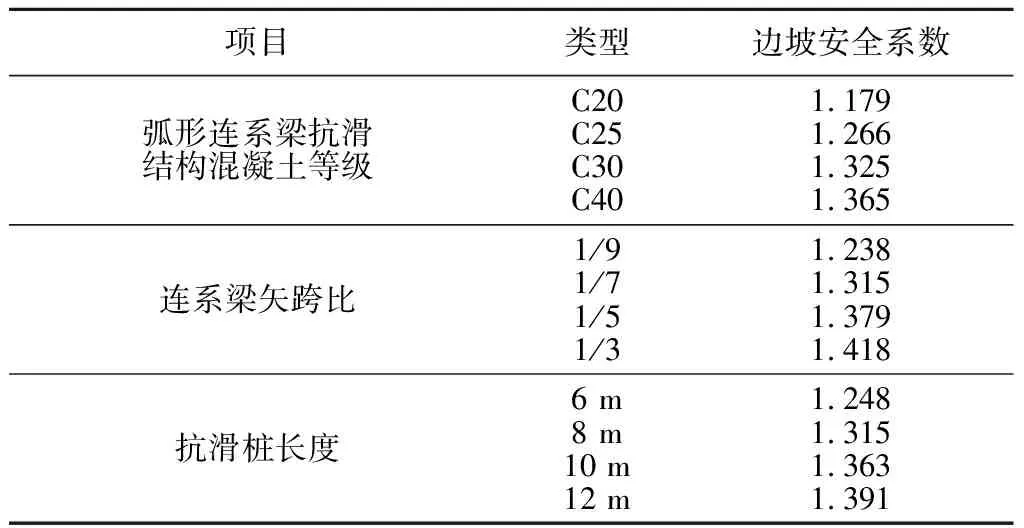
表2 不同参数下边坡的安全系数Tab.2 Safety factor of slope under different parameters
5 结论
通过对悬臂梁抗滑桩的加固效果进行研究,本文提出一种新型的弧形布置的连系梁抗滑桩支挡结构模型,通过分析在不同型式下连系梁抗滑桩的加固效果,得到以下结论。
(1)通过自然边坡和不同型式抗滑桩下的边坡位移对比,得出弧形布置加固效果最优,能有效抑制抗滑桩后方土体滑动面,促进边坡稳定。
(2)弧形连系梁较直梁有一个拱效应的作用,起到良好的承压效果,加固效果大于其他支挡结构,且随着抗滑桩数量的增加,明显提高连系梁抗滑桩整体的抗压性能。
(3)弧形布置抗滑桩在空间上的分布较其他支挡结构能有效的减小边坡塑性区域和剪切应变增量的数值。
(4)一定范围内,增加弧形连系梁抗滑结构混凝土等级,其边坡的安全系数增大,且增大连系梁的矢跨比能有效对边坡进行加固,一定范围内增加抗滑桩的长度能有效抑制边坡滑移。
