(2+1)维Zakharov 方程的自相似变换和线怪波簇激发*

张解放 俞定国 金美贞

1) (浙江传媒学院智能媒体技术研究院,杭州 310018)

2) (浙江省影视媒体技术研究重点实验室,杭州 310018)

3) (浙江传媒学院媒体工程学院,杭州 310018)

4) (浙江传媒学院网络数据中心,杭州 310018)

首先建立(2+1)维(二维空间和一维时间)Zakharov 方程的自相似变换,并将该系统转换为(1+1)维非线性薛定谔(nonlinear Schrödinger,NLS)方程;然后基于该相似变换和已知的(1+1)维NLS 方程有理形式解,通过选择合适参数得到了(2+1)维Zakharov 方程在x-y 平面上丰富的线怪波簇激发,发现产生线怪波簇最大辐值时的传播距离 z 值完全不同,而且形状和幅度可以得到有效调控;最后借助图示展现了二维怪波的传播特征.此外,发现在x-y 平面上,当参数 γ=1 时,呈现线怪波;而当参数 γ1 时,线怪波转变为离散的局域怪波.随参数 γ 的增大,可以在x-y 平面限定区域获得时空局域的怪波,这与Peregrine 在(1+1)维NLS 方程中发现的“Kuznetsov-Ma 孤子”(Kuznetsov-Ma soliton,KMS)或“Akhmediev 呼吸子”(Akhmediev breather,AB)极限情形的“Peregrine 孤子”(Peregrine soliton,PS)类似.本文提出的(2+1)维Zakharov 方程怪波方法可以作为获得高维怪波激发的有效途径,并推广应用于其他(2+1)维非线性系统.

1 引言

怪波概念起源于海洋,用来描述海洋上出现的一种奇怪的海浪,是一种波幅很大、持续时间极短的突然性海浪,对海面上的船只和构建物具有极大的破坏力[1,2].近20 年来,人们普遍认为怪波是一种典型的自然现象[3],由于其奇异的特征、独特的物理机制和有价值的应用背景,引起学术界的强烈兴趣,研究领域从海洋延伸到非线性光学系统[4,5]、等离子体[6]、流体动力学[7,8]、大气[9]、玻色-爱因斯坦凝聚[5]、微波[10]、超流体[11]和金融系统[12],既有丰富的理论成果[13−16],又有重要的实验验证[17−18].

Peregrine[19]在(1+1)维(一维空间和一维时间)非线性薛定谔(nonlinear Schrödinger,NLS)方程中首先发现一种时空双重局域的新型“Peregrine 孤子”(Peregrine soliton,PS),具有“来无影去无踪”特征.Akhmediev 等[20]对NLS 方程的怪波做了比较全面的分析,指出怪波是一种非奇异的有理形式结构,是“Kuznetsov-Ma 孤子”(Kuznetsov-Ma soliton,KMS)或“Akhmediev 呼吸子”(Akhmediev breather,AB)的极限情形,Kedziora等[21]还相继发现了NLS 方程的高阶怪波和多怪波.

实际的物理问题一般由高维非线性波动模型描述,因此有必要对(2+1)维(二维空间和一维时间)或(n+1)维NLS 方程开展研究.近年我们建立了一种自相似变换方法,得到了非自治Kadomtsev-Petviashvili (KP)方程有理函数表示的二维单、双、三怪波解[22]和Fokas 系统的二维怪波激发[23].本文进一步探索自相似变换理论,研究(1)式模型的二维怪波激发及其传播特性,

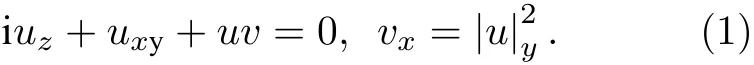
(1)式是由Zakharov 提出的(2+1)维NLS 方程,为区别不同NLS 方程的(2+1)维推广,本文称(1)式为(2+1)维Zakharov 方程[24]其可以改写为以下形式:

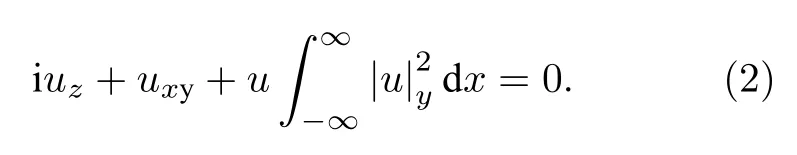
当y=x时,(2)式退化为众所周知的(1+1)维NLS方程;当z=0,(1)式则退化为复式Sine-Gordon方程.Radha 等[25]指出(2+1)维Zakharov方程具有Painlevé性质,并进行了奇异结构分析,给出了双线性形式;Strachan[26]利用双线性方法并通过自由选取的任意函数构造了一类新的诱导局域相干结构的方法;Radha 等[27]利用任意函数得到了单孤子解和双孤子解;Shen 等[28]利用双线性算子方法,给出了同宿轨道解及其所表示的同宿轨道;Wang 等[29]利用动力系统方法和分岔理论,研究了NLS 方程的行波解,得到了有界行波解的可能显式参数表示,并给出了参数空间内的各种相图;Chen 等[30]应用双线性方法求得了呼吸子解和一阶怪波解,还利用Sato 算子理论给出了一阶和高阶怪波解;Wang 等[31]利用双线性方法和长波极限方法得到n孤子的有理解和混合解;Chen等[32]利用朗斯基行列式,给出了一种简便构造呼吸子解和怪波解的有效方法.

本文首先建立(2+1)维Zakharov 方程的自相似变换,然后基于(1+1)维NLS 方程已有的结果,在x-y平面上得到怪波激发;最后给出讨论,列举三个文献[30−32]给出的线怪波作为本文的特例.值得提及的是,本文还发现了x-y平面有限区域内的短寿命怪波,与(1+1)维NLS 方程发现的一维怪波原型相同.

2 (2+1)维Zakharov 方程的自相似变换

为了研究(2+1)维Zakharov 方程引入下列相似变换,

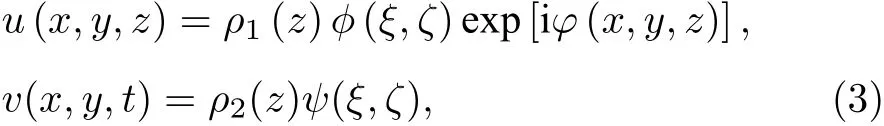
其中ρ1(z),ρ2(z),ϕ(ξ,ζ),ψ(ξ,ζ),φ(x,y,z) 和ξ=ξ(x,y,z),ζ=ζ(z)分别是指定变量的待定函数.从(3)式可以得到

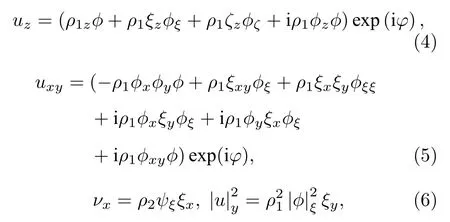
将(4)式—(6)式代入(1)式导出

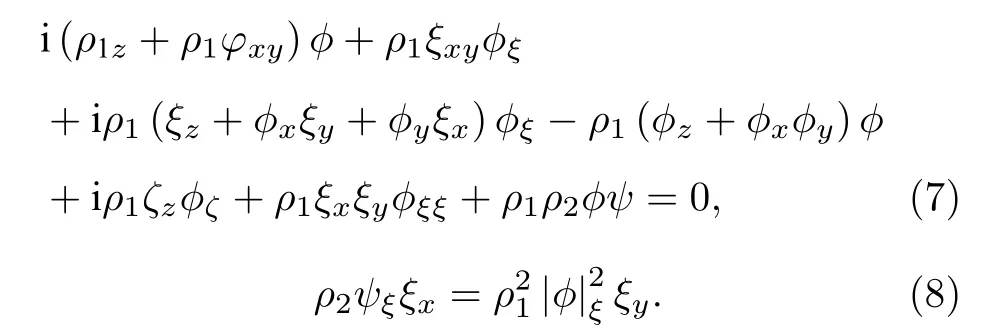
对于(7)式,若ξ(x,t),τ(t),ϕ(x,y,t) 满足下列关系：

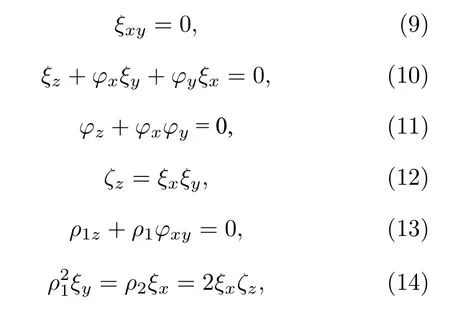
那么(8)式可转化为(1+1)维NLS 方程:

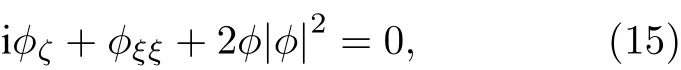
不失一般性,(8)式取积分后的积分常数为0.

鉴于(2+1)维Zakharov 方程对空间变量x,y具有一定的对称性,(9)式可定义相似变量ξ为

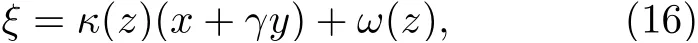
其中κ(z),ω(z) 是关于传播距离z的待定实函数,γ是一个任意常数.结合(16)式,由(10)式可以推定φ(x,y,z) 具有如下形式:

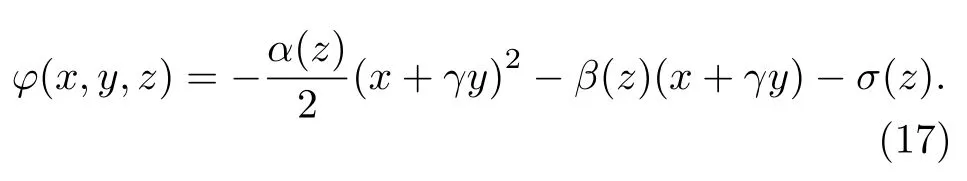
由(10)式—(14)式可求得

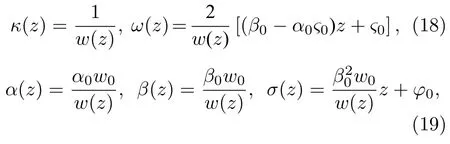
其中w0,ς0,α0,ϕ0,β0为实常数,w(z)=w0(1−2α0z) .整理后得到

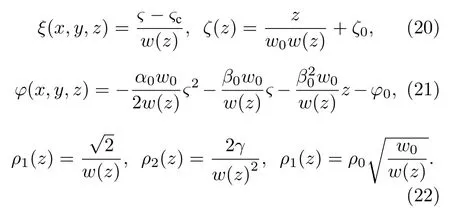
其中

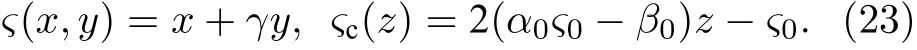
因为ρ0是常数,因此只能选取α0=0,表明在这种情形下该系统不存在啁啾,于是得到

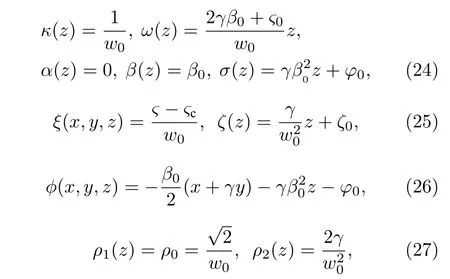
其中ςc(z)=−(ς0+2γβ0z) 为脉冲的中心位置.综上可知该系统的脉冲宽度为w0,相位φ(x,y,z)=−β0(x+γy)−−φ0,振幅扩大系数为/w0.

通过自相似变换(3)式,把(2+1)维Zakharov方程映射为(1+1)维NLS 方程.(15)式是一个可积系统,已有各类解析和数值方法研究,并得到了行波解、亮孤子解、暗孤子解、呼吸子解和有理数解等丰富结果.下面借助(15)式的相关结果,深入研究(1)式的二维怪波激发.

3 线怪波簇激发及其传播特性

下面考虑(2+1)维NLS 方程(1)式或(2)式的线怪波激发和动力学传播特征.众所周知,(1+1)维NLS 方程具有如下形式的怪波解,

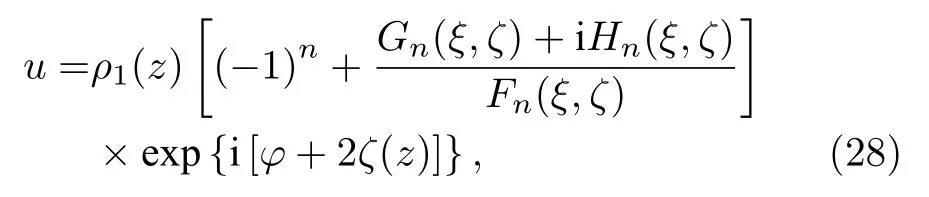
其 中n(=1,2,3,···) 是正整数,Gn(ξ,ζ),Hn(ξ,ζ),Fn(ξ,ζ)是有理多项式函数,并要求多项式Fn(ξ,ζ)在积分区域不为0,且可以用不同的方法求得.

值得指出的是,(2+1)维Zakharov 方程的一阶线怪波激发,即(28)式是关于坐标x,y的线性组合坐标ξ,ζ和传播距离z表示的有理形式解.考虑到实际物理背景,譬如光学上研究的波导介质截面,水动力学研究的水表面等,需要在平面上讨论(2+1)维Zakharov 方程的怪波解才有实际意义.类比于KP 方程的线孤子解,在x-y平面上分析讨论(1)式的线怪波动力学传播特性.

对n=1,有

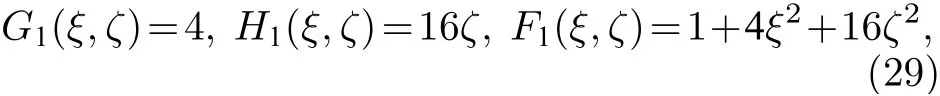
则(28)式成为

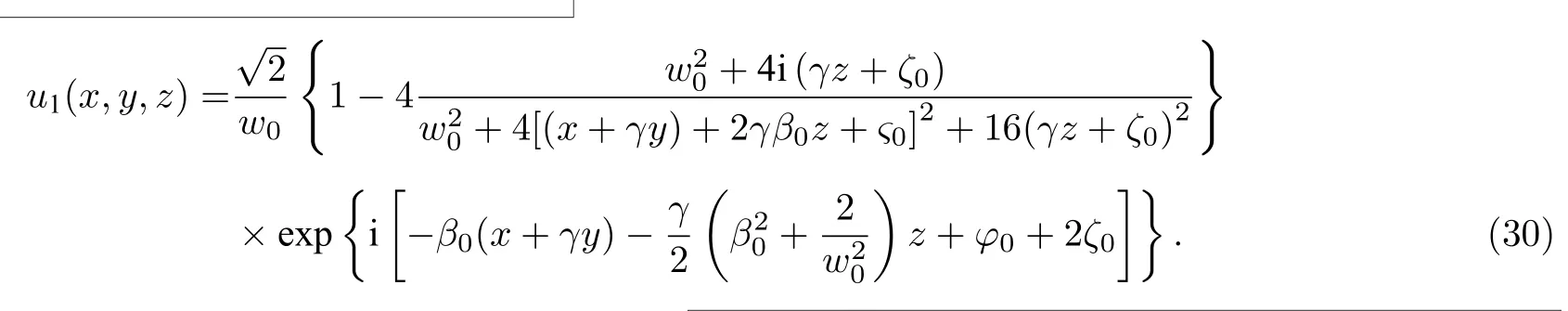
通过选择适当的自由参数值,由(30)式可得到(1)式的一阶线怪波演化图.图1(a),(b),(c)分别是当传播距离z=−3,0,1 时一阶线怪波在x-y平面上的三维图,A表示该位置时一阶线怪波的最大幅值;(d),(e),(f)分别是对应的投影图,参数值为w0=γ=β0=1,ς0=ζ0=φ0=0 .

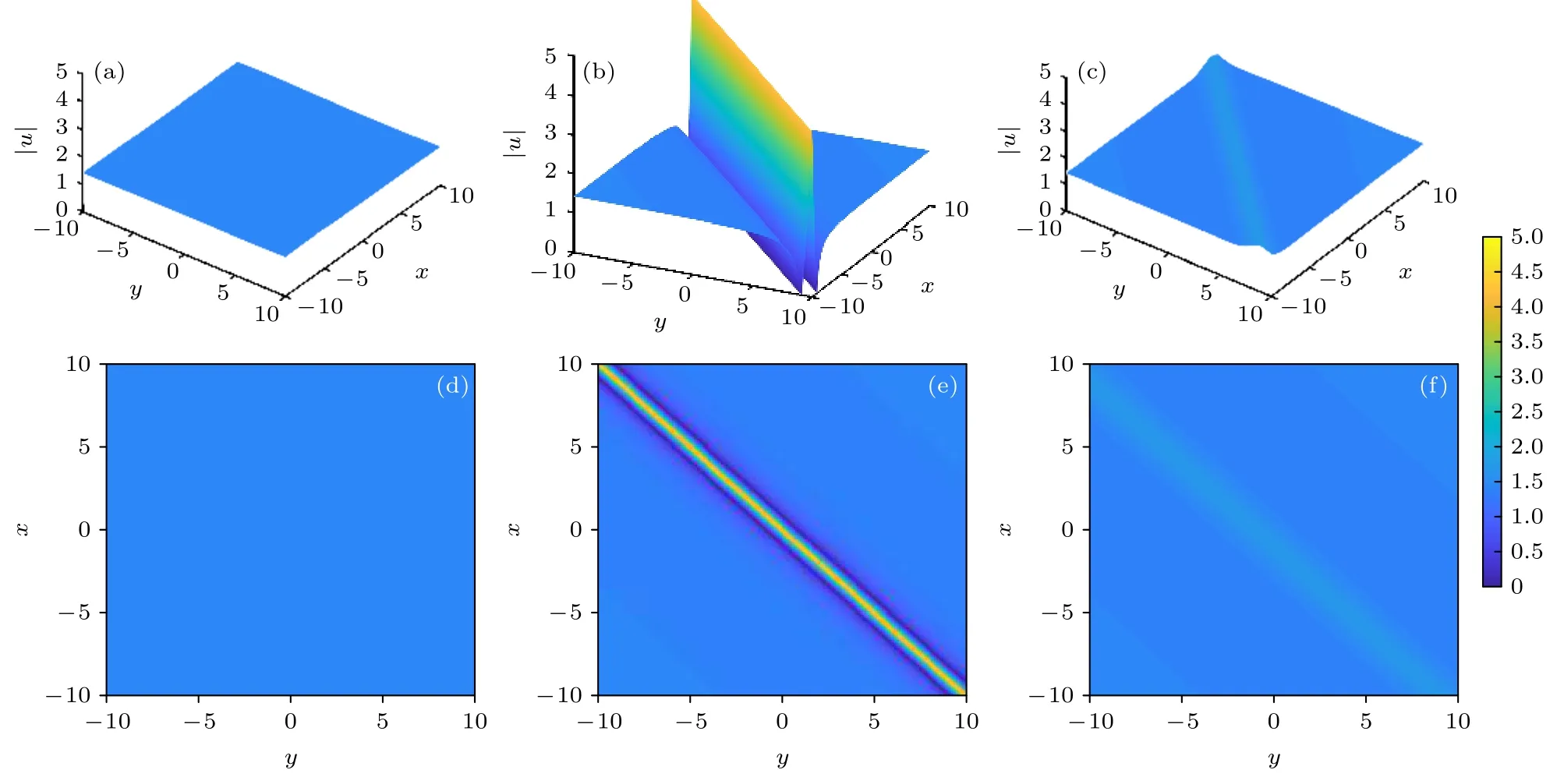
图1 传播距离 z=−3,0,1 时一阶线怪波 |u| (a),(b),(c) 三维图;(d),(e),(f) 对 应x-y 面上的投影图;(a),(d) A=1.45;(b),(e) A=4.24;(c),(f) A=1.71Fig.1.One-order line rogue wave |u| respectively at the propagation distance z=−3,0,1 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=1.45;(b),(e) A=4.24;(c),(f) A=1.71.

对n=2,G2(ξ,ζ),H2(ξ,ζ),F2(ξ,ζ) 可以有多种不同的形式.若选取

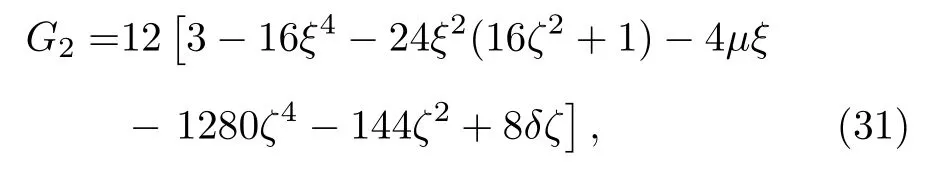
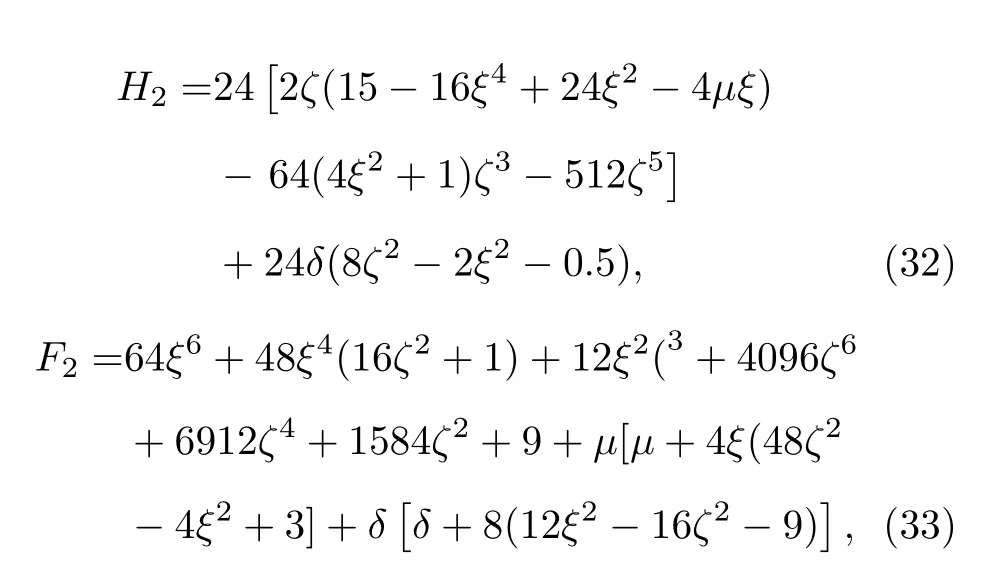
则(28)式成为

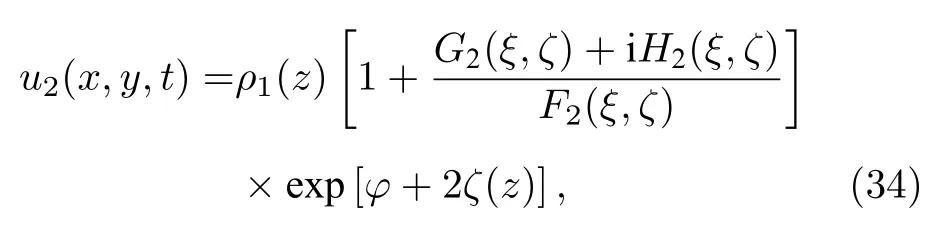
其中ρ1,ξ,ζ,φ由相似变换(25)式—(27)式表示,ς(x,y),ςc(z)由(23)式给出.由于(34)式中µ,δ是任意常参数,因此具有多种不同的结构.最简单的情况是µ=δ=0,通过选择适当的自由参数值,由(34)式可得到(1)式的二阶线怪波演化图.图2(a),(b),(c)分别是当传播距离z=−3,0,1 时在x-y平面上的二阶怪波的三维图,(d),(e),(f)分别是对应的投影图,参数取值为w0=γ=β0=1,ς0=ζ0=ϕ0=µ=δ=0.

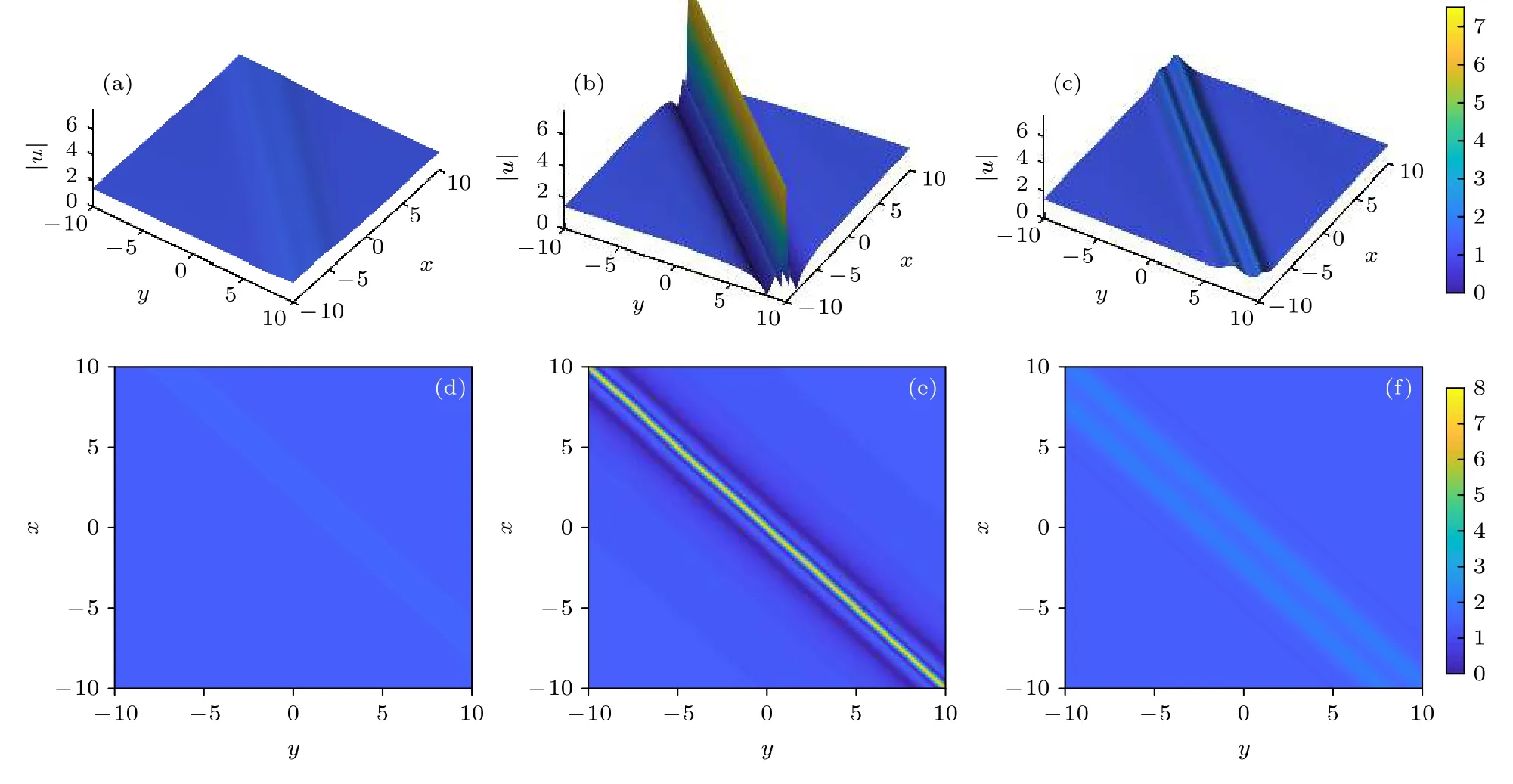
图2 传播距离 z=−3,0,1 时二阶线怪波 |u| (a),(b),(c)三维图;(d),(e),(f) 对 应x-y 面上的投影图;(a),(d) A=1.58;(b),(e) A=7.32;(c),(f) A=1.93Fig.2.Two-order line rogue wave |u| respectively at the propagation distance z=−3,0,1 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=1.58;(b),(e) A=7.32;(c),(f) A=1.93.

当µ,δ都不为0 时,(34)式描述的是(2+1)维Zakharov 方程的线怪波簇(rogue wave cluster,RWC).具有以下5 种情况:1)µ=100,δ=0;2)µ=0,δ=100;3)µ=40,δ=20;4)µ=20,δ=−20 ;5)µ=−20,δ=20.这5 种情况分别对应图3—图7,其中各图的(a),(b),(c)图分别是不同传播距离z时在x-y平面上线怪波簇的三维图,(d),(e),(f)图对应投影图,其他参数取值为w0=γ=β0=1,ς0=ζ0=φ0=0.这5 种情况虽描述的都是线怪波簇,但产生线怪波簇最大辐值A的传播距离z值(位置)和形状完全不同,参数选取具体见图3—图7中说明.

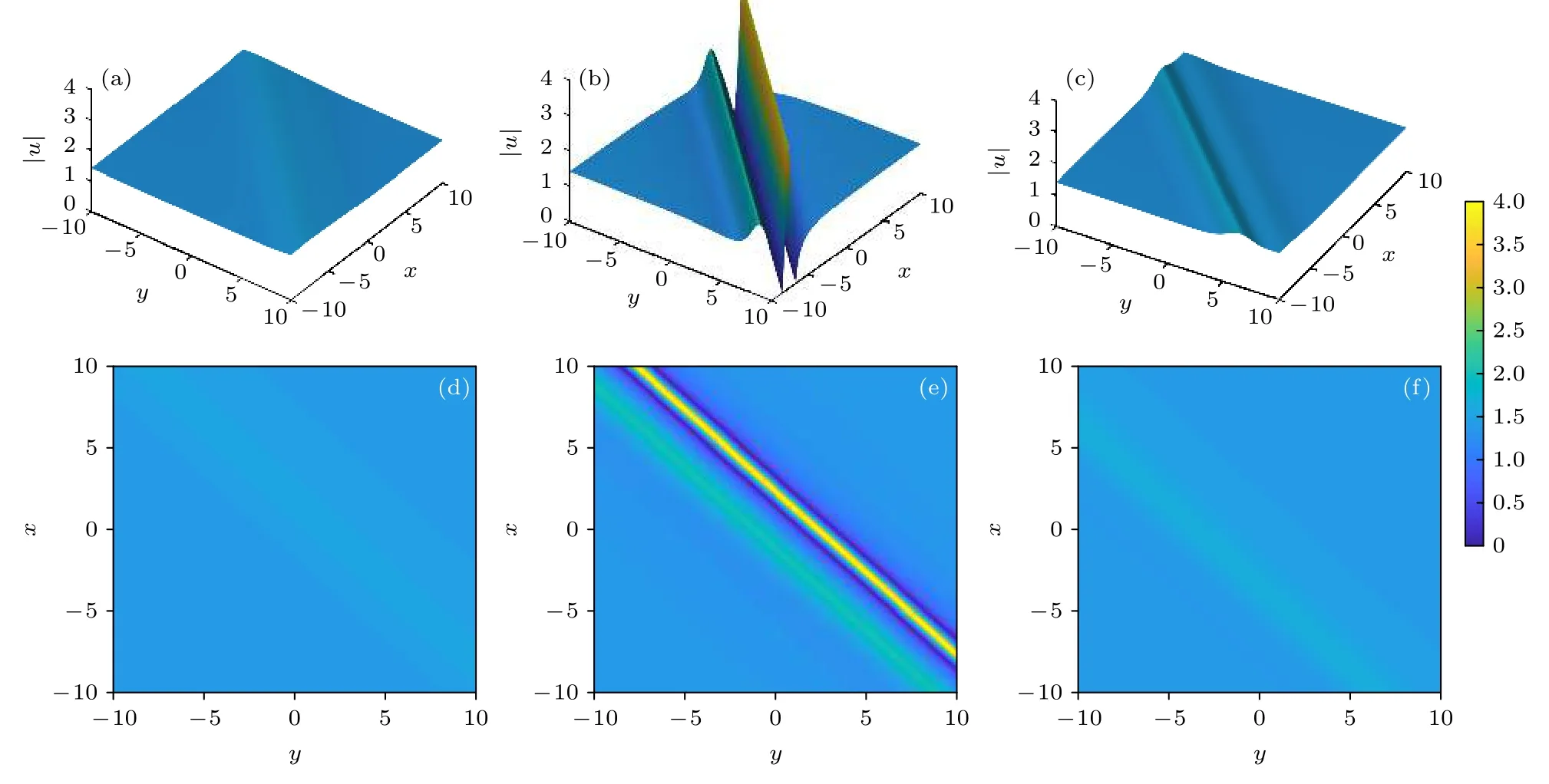
图3 传播距离 z=−3,0, 2 时二阶线怪波 |u| (a),(b),(c) 三维图;(d),(e),(f) 对应x-y 面上的投影图;(a),(d) A=1.52;(b),(e) A=3.99;(c),(f) A=1.69;参数w0=γ=β0=1,ς0=ζ0=φ0=δ=0,µ=100Fig.3.Two-order line rogue wave |u| respectively at the propagation distance z=−3,0, 2 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=1.52;(b),(e) A=3.99;(c),(f) A=1.69;the parameters are w0=γ=β0=1,ς0=ζ0=φ0=δ=0, µ=100 .

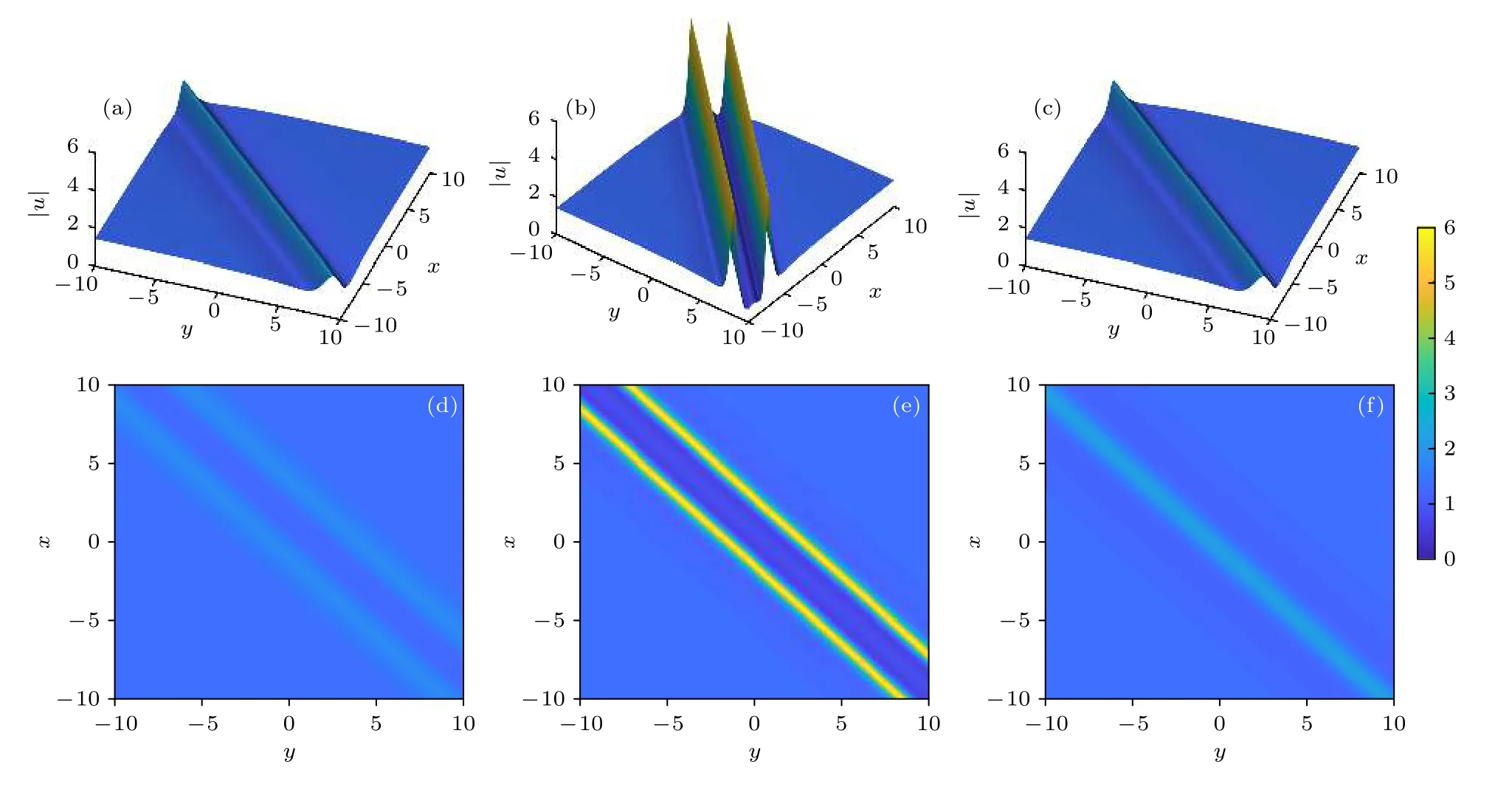
图4 传播距离 z=−1.5, −0.635, 0.5 时二阶线怪波簇 |u| (a),(b),(c) 三维图;(d),(e),(f) 对应x-y 面上的投影图;(a),(d) A=1.80;(b),(e) A=5.81;(c),(f) A=2.23;参数w0=γ=β0=1,ς0=ζ0=φ0=µ=0,δ=100Fig.4.Two-order line rogue wave |u| respectively at the propagation distance z=−1.5, −0.635, 0.5 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=1.80;(b),(e) A=5.81;(c),(f) A=2.23;the parameters are w0=γ=β0=1,ς0=ζ0=φ0=µ=0,δ=100 .

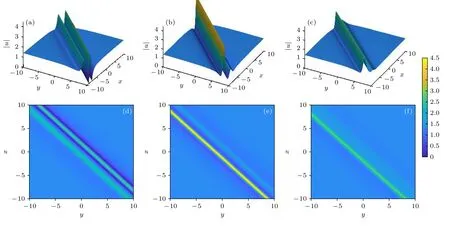
图5 传播距离 z=0,0.5,1.0 时二阶线怪波簇 |u| (a),(b),(c)三维图;(d),(e),(f) 对应x-y 面上的投影图;(a),(d) A=2.76;(b),(e) A=4.36;(c),(f) A=2.78;参数w0=γ=β0=1,ς0=ζ0=φ0=0,µ=40,δ=20Fig.5.Two-order line rogue wave |u| respectively at the propagation distance z=0,0.5,1.0 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=2.76;(b),(e) A=4.36;(c),(f) A=2.78;the parameters are w0=γ=β0=1,ς0=ζ0=φ0=0,µ=40,δ=20 .

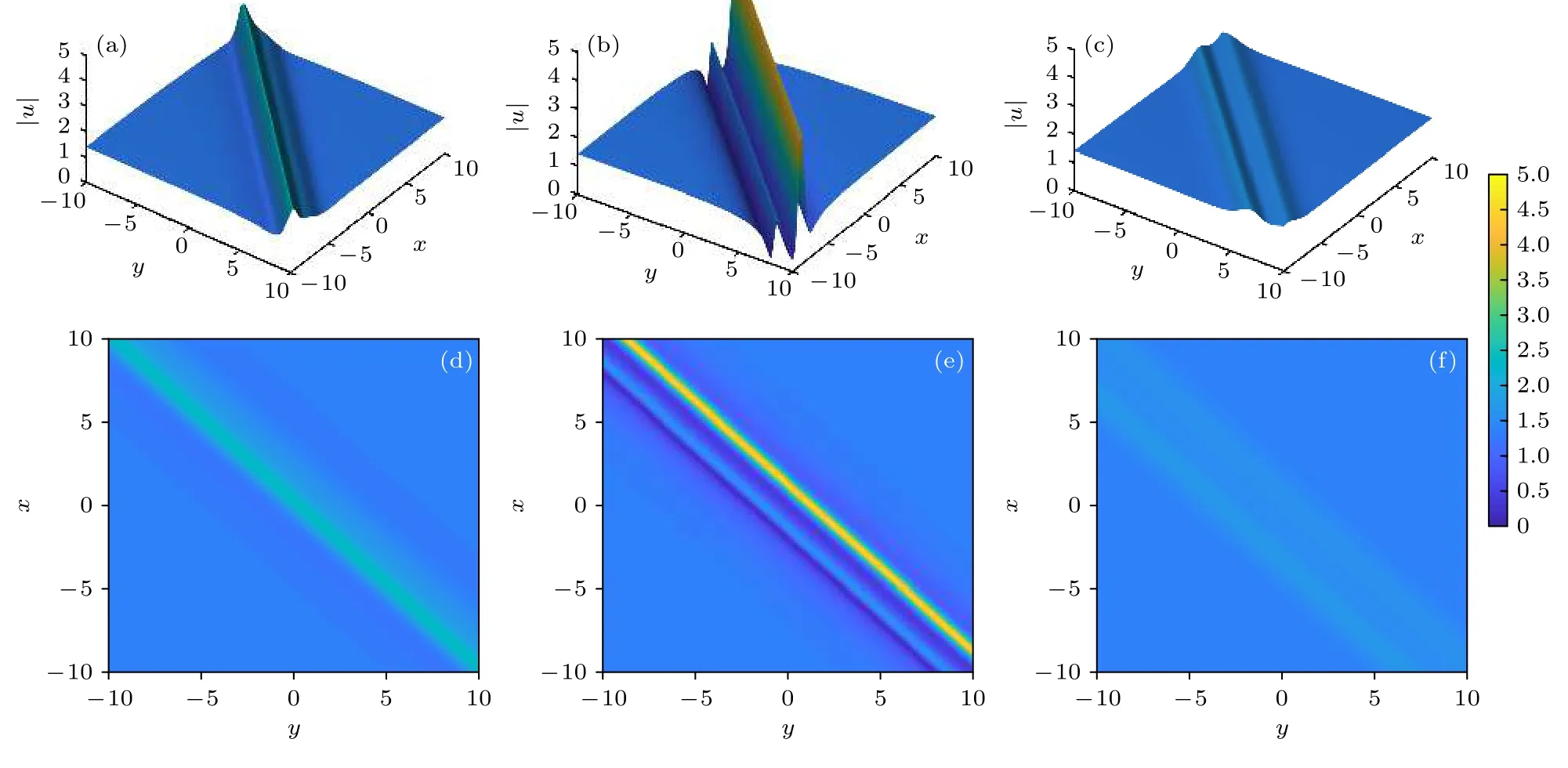
图6 (a),(b),(c)传播距离 z=−1,0.29,1.5 时二线怪波簇 |u| 在x-y 平面上的三维图;(d),(e),(f)对应的投影图;(a),(d) A=2.76;(b),(e) A=4.53;(c),(f) A=1.72;参数w0=γ=β0=1,ς0=ζ0=φ0=0,µ=20,δ=−20Fig.6.Two-order line rogue wave |u| respectively at the propagation distance z=−1,0.29,1.5 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=2.76;(b),(e) A=4.53;(c),(f) A=1.72;the parameters are w0=γ=β0=1,ς0=ζ0=ϕ0=0,µ=20,δ=−20 .

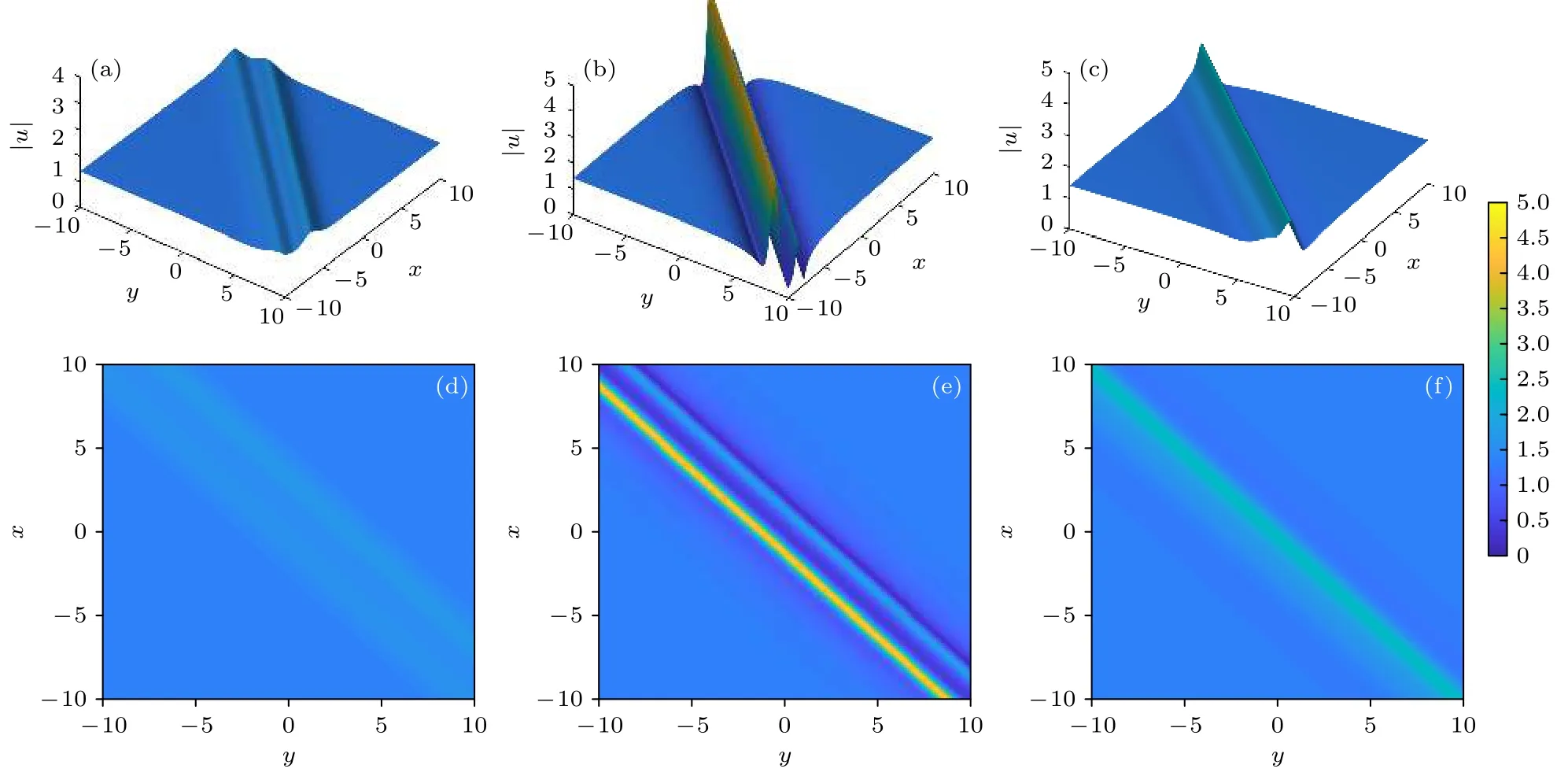
图7 传播距离 z=−1.5, −0.295,1 时二阶线怪波簇 |u| (a),(b),(c) 三维图;(d),(e),(f)对应x-y 面上的投影图;(a),(d) A=1.72;(b),(e) A=4.39;(c),(f) A=2.39;参数w0=γ=β0=1,ς0=ζ0=φ0=0, µ=−20,δ=20Fig.7.Two-order line rogue wave |u| respectively at the propagation distance z=−1.5, −0.295,1 :(a),(b),(c) Three-dimensional plots;(d),(e),(f) the corresponding contour plots in the x-y plane;(a),(d) A=1.72;(b),(e) A=4.39;(c),(f) A=2.39;the parameters are w0=γ=β0=1,ς0=ζ0=ϕ0=0, µ=−20,δ=20 .

对于高阶线怪波和其他形式结构的怪波都可以做类似研究,限于篇幅这里不深入讨论.由图1—图7 可以看出,在真实的x-y平面上线怪波簇呈现出类似线孤子的形态,产生线怪波的背景值都是1.42.但与线孤子不同的是,其峰值不仅很大,而且衰减极快,具有怪波的大振幅、短寿命特征.

当宽度w0确定后,只有参数γ对一阶线怪波的形态产生影响.图8 展现了一阶怪波(30)式在x-y平面上随参数γ在z=0 时的不同形态,和图1—图7 一样,随z快速衰减,具有怪波的大振幅、短寿命特征.可以看出,在x-y平面上,随γ的取值变化,一阶线怪波转变为分立的怪波.当γ=15 时,在区间 [−10,10] 的x-y平面上呈现局域的单个短寿命怪波.当γ=20 时,在区间 [−20,20] 的x-y平面上呈现局域的单个短寿命怪波.值得注意的是,脉冲宽度w0影响怪波的幅值和形状,β0对怪波产生的位置和形状基本没有影响,ς0,ζ0影响怪波的产生位置但不影响怪波的形状.图8 给出了当z=0时,一阶线怪波在x-y平面上不同参数γ下的形态,各分图一阶线怪波的最大幅值A=6.36,其中参数值为w0=2/3,β0=1,ς0=ζ0=ϕ0=0 .

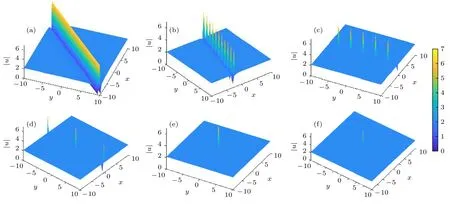
图8 在 z=0 时,一阶线怪波 |u| 在x-y 平面上不同参数 γ 下的形态 (a) γ=1 ;(b) γ=3 ;(c) γ=6 ;(d) γ=10 ;(e) γ=15 ;(f) γ=20Fig.8.One-order rogue wave |u| in the x-y plane under the different γ at the propagation distance z=0 :(a) γ=1 ;(b) γ=3 ;(c) γ=6 ;(d) γ=10 ;(e) γ=15 ;(f) γ=20 .

4 结论

本文构造的(2+1)维Zakharov 方程线怪波激发不仅丰富,而且具有一般性.Chen 等[30]应用Hirota 双线性算子方法得到如下形式的(2+1)维Zakharov 方程

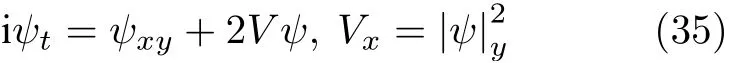
的周期解和极限情形的一阶怪波解,同时在NLS方程的Grammian 行列式解的基础上,利用Sato算子理论得到方程的一阶和高阶怪波解.如一阶线怪波为

Wang 等[31]应用Hirota 双线性算子方法得到如下形式的(2+1)维Zakharov 方程

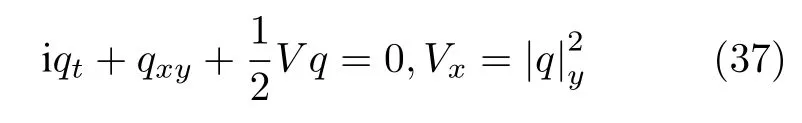
的怪波解

Chen 等[32]应用Hirota 双线性算子方法得到如下形式的(2+1)维Zakharov 方程

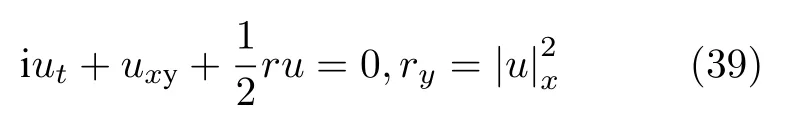
的线怪波为

总之,本文研究建立了(2+1)维Zakharov 方程的自相似变换理论,得到了它的类似KP 方程线孤子特征的线怪波激发,并通过选用合适的参数用图像分别刻画了一阶线怪波和二阶线怪波的传播特性.特别指出,在x-y平面上,当参数γ=1 时,呈现线怪波;而当参数γ1 时,线怪波变为似梳子怪波,并随参数γ的增大,怪波间距不断变大,可以在要求的平面区域内获得二维空间全局域的短寿命的怪波.这与Peregrine[20]在(1+1)维NLS方程中发现的PS 类似,是KMS 或AB 的极限情形.

本文提出的(2+1)维Zakharov 方程的自相似变换方法,不仅减少了研究高维问题的复杂运算,而且给出了构造高维怪波激发的有效机制,提供了比文献[33−40]更丰富的包括怪波在内的局域相干结构.本文思路可应用于Fokas 系统和Davey-Stewartson 模型,相关研究进行中.