多尺度波致流非饱和孔隙介质波传播理论研究*

李红星 张嘉辉 樊嘉伟 陶春辉 肖昆 黄光南 盛书中 宫猛

1) (东华理工大学,核资源与环境国家重点实验室,南昌 330013)

2) (自然资源部第二海洋研究所,杭州 310012)

弹性波在非饱和孔隙介质中传播时,孔隙流体会发生宏观Biot 流、微观喷射流以及由于孔隙流体不同(气、液双相)导致的介(中)观流.将非饱和孔隙介质等效为含液相孔隙流体的背景介质中嵌入含气相孔隙流体的包裹体,在非饱和双重孔隙介质模型基础上,引入微观喷射流,建立了包含宏观、微观和介观三种尺度波至流的非饱和孔隙介质波传播方程.数值分析表明该模型可以更好地预测更宽频带内的波速频散和衰减.

1 引言

油气储层和海洋底质都是典型的多相孔隙介质,孔隙介质弹性波传播理论对于油气储层地震预测、海洋底质声学探测都具有重要的意义.弹性波在非饱和孔隙介质中传播时,孔隙流体在波动作用下会发生三种运动:沿波传播方向的宏观Biot 流动,垂直于波传播方向的微观喷射流动以及由于孔隙流体非饱和(等效为含液相孔隙流体的孔隙介质中嵌入介观尺度的含气相孔隙流体的孔隙介质)而产生的介观局域性流体流动.目前,学术界普遍认同这三种孔隙流体波致流机制是导致孔隙介质中弹性波发生耗散和频散的最主要原因.Biot[1−3]对孔隙介质中波传播时的宏观波致流运动机制进行了系统的研究,建立了Biot 理论.Biot 流可以预测到高频(声波-超声波频段)弹性波的速度频散和衰减,但预测结果远小于实测值,并且无法预测低频弹性波(地震波频段)速度频散和衰减.Mavko[4,5]对波传播过程中,孔隙介质中的微观尺度波至流进行了研究,提出了喷射流机制.喷射流可以预测到高频弹性波更高的速度频散和衰减,能更好地拟合实测值,但仍然无法预测低频弹性波(地震波频段)速度频散和衰减.White[6,7]基于等效球状介质模型,首次建立了包含介观尺度波至流的波传播理论.Duuta[8],Dutta 和Seriff[9],Johnson[10],Pride和Berryman[11]分别在White 模型的基础上,进一步完善了介观尺度的孔隙流体局部流动机制.介观流可以更好地预测低频弹性波(地震波频段)速度频散和衰减,但无法很好地预测高频(声波-超声波频段)弹性波的速度频散和衰减.Dvorkin 和Nur[12]建立了包含宏观尺度及微观尺度两种波至流机制的孔隙介质波传播理论,即BISQ 理论.Li 等[13],Yang 和Chen[14],Diallo 和Appel[15]分别从不同角度发展或改进了BISQ 模型.巴晶等[16−20]研究了双孔介质模型,将流体的宏观尺度及中观尺度波至流机制结合在一起,推导得到了双重孔隙介质模型 (BR 模型).2018 年,Zhao 等[21]将White周期层状介质模型与双孔介质理论相结合,建立了层状双孔模型.2020 年,胡亚元[22]把双重孔隙介质视为两个单重孔隙介质的嵌套叠加,从经典混合物理论出发推导了非饱和双重孔隙介质的能量守恒方程.目前,将三种尺度的波至流统一考虑在一个孔隙介质波传播理论中的研究较少.本文将非饱和孔隙介质等效为含液相孔隙流体的背景介质中嵌入含气相孔隙流体的包裹体,在非饱和双重孔隙介质模型基础上,引入微观喷射流,建立了包含宏观、微观和介观三种尺度波至流的非饱和孔隙介质波传播理论(简称:BRS 模型).通过数值模拟分析,BRS 理论可以在全频段范围预测弹性波速度频散和衰减,为油气储层地震预测和海洋底质声学探测提供理论基础.

2 多尺度波至流非饱和孔隙介质波传播理论

将非饱和孔隙介质(宏观尺度,图1(a))等效为含液相孔隙流体的背景介质中嵌入含气相孔隙流体的包裹体(介观尺度,图1(b)),在背景介质和包裹体中都存在由固相颗粒的接触产生的微观孔隙(图1(c)).为了简化模型,用七个等边长的正方体组合而成的“十字型”结构等效嵌入的含气相孔隙流体的包裹体(图2).非饱和孔隙介质特征单元中发生三种尺度的波至流:和波传播方向一致的宏观Biot 流,垂直波传播方向的微观喷射流,体现包裹体与背景介质之间的流体交换的中观局部流(图2).模型假设:1) 背景介质和嵌入包裹体分别都是单一孔隙结构,均可发生Biot 宏观和微观喷射波至流,在波传播时,包裹体内外发生流体交换,产生介观波至流;2) 在孔隙介质中,包裹体的体积占比较小,并且均匀分布在背景介质中;3) 忽略两类孔隙流体表面张力作用对孔隙流体流动的影响,忽略孔隙流体与固相介质骨架颗粒之间的化学作用.

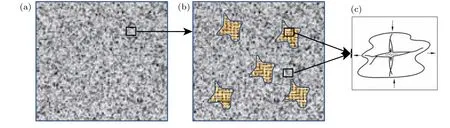
图1 孔隙介质示意图 (a) 宏观尺度;(b) 介观尺度;(c) 微观尺度Fig.1.Schematic diagram of porous media:(a) Macro scale;(b) mesoscopic scale;(c) micro scale.

根据Biot[1−3]对势能函数的定义,引入ζ描述弹性波作用下非饱和孔隙介质产生的局域性流体流动的流体体应变增量,岩石内部的弹性应变势能函数为[16]

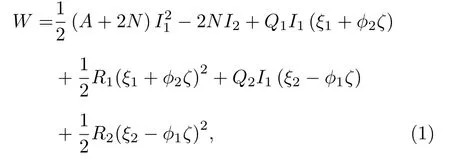
其中I1=e为固相体应变;I2为固相切应变相关量;ξ1,ξ2为背景介质与包裹体孔隙流体的体应变;ϕ1=v1·ϕ0,ϕ2=v2·ϕ0,v1,v2=1−v1分别表示背景介质和包裹体的体积占比,ϕ0表示孔隙介质孔隙度.A,N,Q1,Q2,R1,R2为双重孔隙介质6 个独立的弹性参数[16]:

其中ϕ=ϕ1+ϕ2=ϕ0;Kb为孔隙介质骨架体积模量;Ks为固相颗粒体积模量;µb为骨架剪切模量;为背景介质孔隙流体体积模量;为包裹体孔隙流体体积模量.根据模型示意图2,在单位系统中,有效流体体积变化为[20]ϕ1ζ ≈1−V0/V.V0是静态时嵌入包裹体的体积,V是波传播作用下,动态时包裹体的体积,那么ζ可表达为

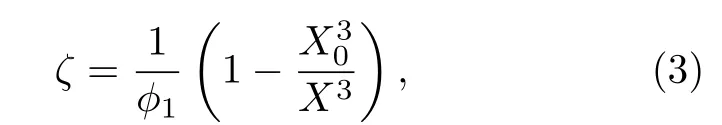
其中X表示波传播作用下“十字型”嵌入包裹体等效正方体的动态边长;X0表示静态时包裹体等效正方体的边长(图2).

图2 介观尺度孔隙介质等效特征单元 (a) 三维示意图;(b) 二维示意图Fig.2.Equivalent characteristic unit of mesoscopic porous media:(a) Three-dimensional schematic diagram;(b) twodimensional schematic diagram.

部分饱和孔隙介质中,动能函数可写为[16]

x=X时,应力、应变满足连续边界条件.参考Rayleigh[23](1917)对气泡膨胀过程速度的定义,根据动能定理,非饱和孔隙介质特征单元中包裹体外的动能表达如下:

联合(5)式和(6)式,可以得到

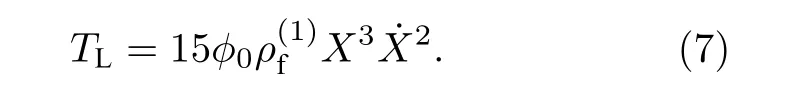
单位特征单元中,“十字型”包裹体的体积占比为v2=7X03≈7X3,且ϕ2=v2ϕ0,可以得到

由(3)式可得

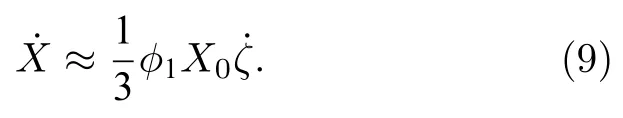
因此,动能密度可进一步表示为

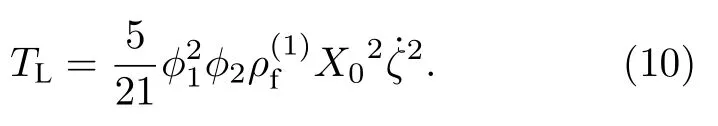
根据Biot[1−3]对耗散函数的定义,将其扩展到一类骨架,两类流体的部分饱和孔隙介质中:

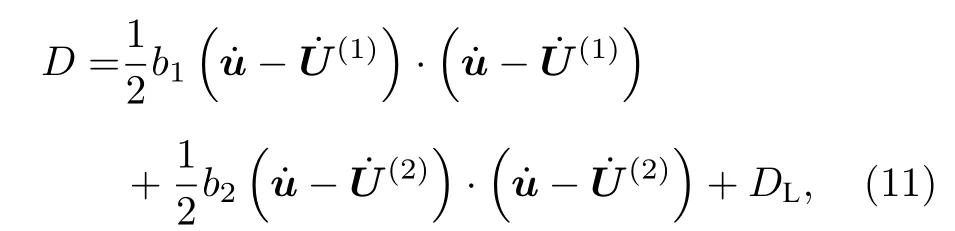
其中bi表示耗散系数,分别是固相、背景介质孔隙流体、包裹体孔隙流体的振动速度向量;DL表示介观尺度局域性孔隙流体流动所产生的耗散,与动能函数的推导过程类似,DL可表示为

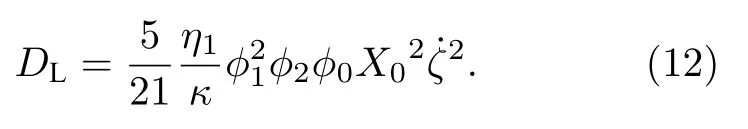
根据双重孔隙模型推导过程[16,20],将(1)式、(4)式及(10)式—(12)式代入含阻尼的拉格朗日方程[24],可得到“十字型”非饱和双重孔隙介质波传播方程:

将(15)式代入(14)式中,并用(14)式的孔隙流体压力代替(13)式的孔隙流体压力项,即为统一考虑宏观、介观和微观波至流的多尺度波至流非饱和孔隙介质波传播方程(BRS 模型).将波动方程(13)中的固相位移、流体位移及流体体应变增量写为平面波解的形式 exp i(ωt −k·z),将之代入(13)式中,经整理可得:

求解(16)式,得到波数k,进而得到波的传播速度和品质因子:

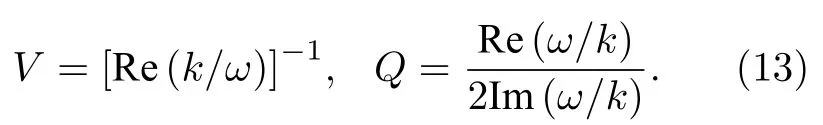
3 数值分析

为了进一步分析多尺度波至流非饱和孔隙介质波传播特征,设定孔隙介质模型(表1),对比Biot 理论、BISQ 模型、BR 模型以及BRS 模型预测的波传播速度与衰减特征,分析介质参数对BRS 模型预测波传播速度与衰减的影响.从1 Hz—100 MHz 范围内的波传播速度和逆品质因子预测结果(图3)可得一下结论.

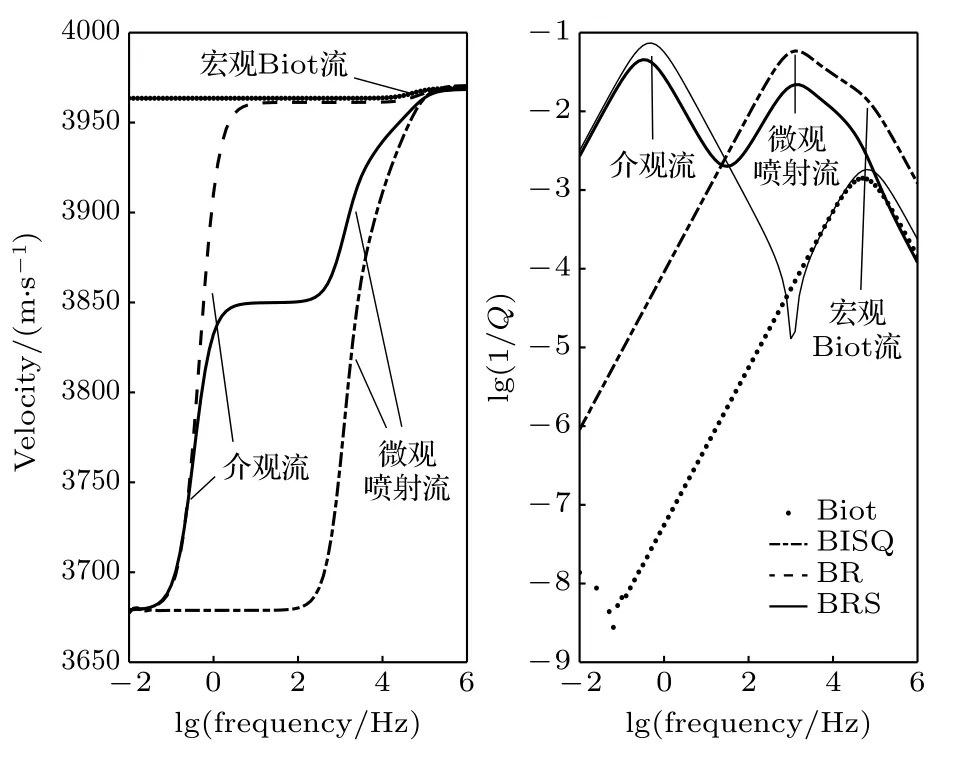
图3 不同孔隙介质模型波传播速度与衰减对比Fig.3.Comparison of wave propagation velocity and attenuation in porous media between different models.

表1 非饱和孔隙介质模型参数Table 1.Parameters of unsaturated porous media model.

1) BISQ,BR 和BRS 模型预测的波速频散的低频极限和高频极限基本一致,高频极限趋近于Biot 预测值.Biot 预测波速只在高频端存在微弱频散过渡带,说明宏观波至流产生的频散很小.BISQ 预测波速在高频端存在明显频散过渡带,说明BISQ 在宏观流基础上引入的喷射流,可导致高频端产生更大频散.BR 预测波速在高频端的频散过渡带与Biot 一致,在低频端存在明显频散过渡带,说明BR 在宏观流基础上引入的介观流,可导致低频端产生更大频散.BRS 预测波速在低频端和高频端都存在明显频散过渡带,综合体现了宏观流、喷射流和介观流产生的波速频散,更有利于解释更宽频带范围观测到的频散现象.

2) Biot 预测的衰减总体上最低,可以观察到宏观Biot 流导致的波衰减峰值.BISQ 预测的衰减和Biot 预测衰减总体趋势一致,但衰减值更高,可以观察到微观喷射流导致的波衰减峰值和微弱的宏观Biot 流导致的波衰减峰值.BR 预测的衰减在高频端和Biot 预测结果相当,可观察到宏观Biot 流导致的波衰减峰值,此外,BR 预测衰减在低频端远高于Biot 和BISQ 模型预测结果,可观察到介观流导致的波衰减峰值.BRS 预测衰减在高频端接近BISQ 预测结果,能观察到微弱宏观Biot 流和明显微观喷射流导致的波衰减峰值,BRS 预测衰减在低频端接近BR 模型预测结果,可观察到介观流导致的波衰减峰值.

下面分析主要孔隙介质参数对BRS 模型预测的波传播速度和衰减的影响.随着孔隙度的增加,波速整体减小,波速频散总体趋势和过渡带所在频率范围基本保持不变,波衰减在频散过度带频带范围内总体随孔隙度增大而增大(图4),这是由于孔隙流体的弹性模量比固相骨架低,孔隙度增大,造成孔隙流体占比成比例增大,造成速度在整个频带范围内降低,同时,孔隙度的增加会增大固流耦合和相对运动,从而产生更高的衰减.随着背景介质占比(也即液相流体饱和度)的降低,波速变小,代表介观流的衰减峰向高频方向移动,但代表喷射流的衰减峰变化较小(图5),说明随着液相饱和度的减小,孔隙流体等效弹性模量降低,进而导致孔隙介质波速减小,同时,介观流受孔隙流体参数的影响远高于微观流.随着介观包裹体尺度增大,代表介观流的波速频散过渡带和衰减峰向低频方向移动,而代表喷射流的频散过渡带和衰减峰则没有变化(图6),这是由于包裹体尺度仅影响介观流,包裹体尺寸越大,介观流导致的低频弹性波频散和衰减越明显.随着渗透率的增加,波速和衰减曲线整体向高频方向移动(图7).需要说明的是,孔隙介质参数对孔隙介质中弹性波的衰减及波速频散的影响满足复杂的非线性关系((16)式和(17)式),各参数之间相互耦合,因此,针对具体实际问题(如油气储层或海底),根据描述孔隙介质波传播的方程计算结果,评价孔隙参数对孔隙介质波传播速度与衰减的影响更具客观和具有实际价值.

图4 不同孔隙度BRS 模型预测的波速与衰减Fig.4.Wave velocity and attenuation predicted by BRS model with different porosity.

图5 不同饱和度BRS 模型预测的波速与衰减Fig.5.Wave velocity and attenuation predicted by BRS model with different saturation.

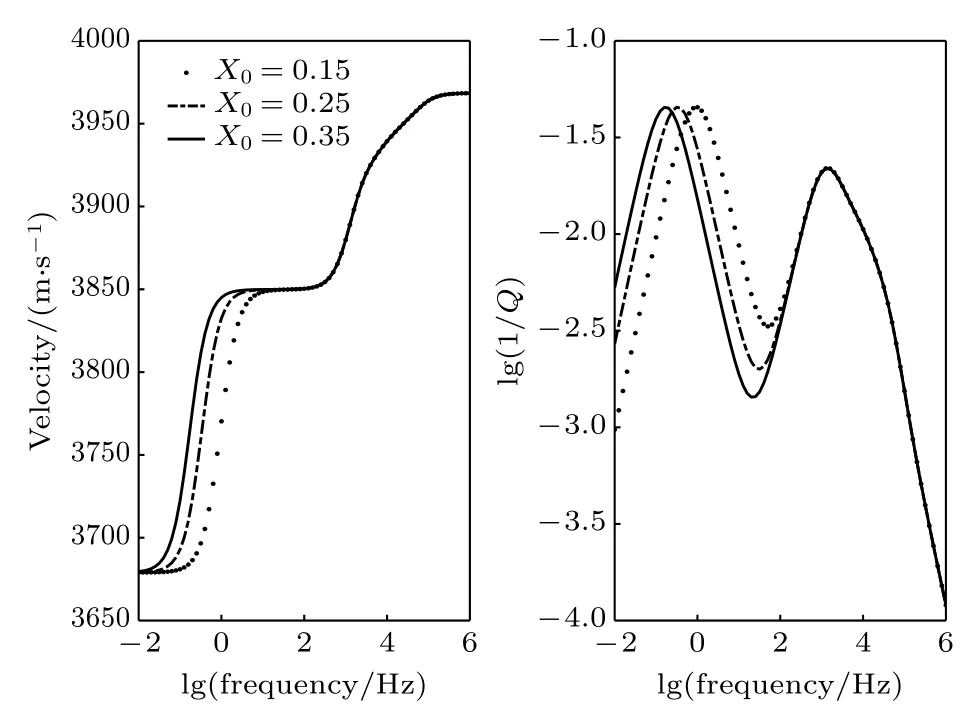
图6 不同介观尺度BRS 模型预测的波速与衰减Fig.6.Wave velocity and attenuation predicted by BRS model with different saturation.

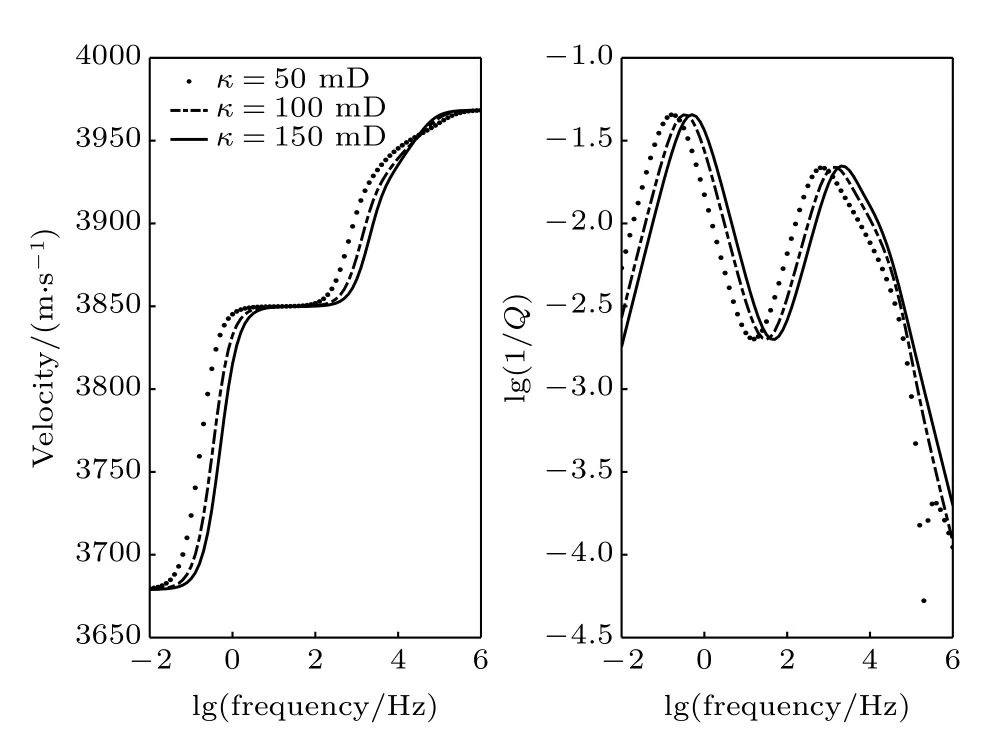
图7 不同渗透率BRS 模型预测的波速与衰减Fig.7.Wave velocity and attenuation predicted by BRS model with different permeability.

4 结论

将非饱和孔隙介质等效为含液相孔隙流体的背景介质中嵌入含气相孔隙流体的包裹体,在非饱和双重孔隙介质模型基础上,引入微观喷射流,建立了包含宏观、微观和介观三种尺度波至流的非饱和孔隙介质波传播方程.

1) Biot 模型仅能在高频端预测微弱的波速度频散,预测衰减较小;BISQ 模型可以解释较高频段的强速度频散和高衰减;BR 模型可以解释较低频段的强速度频散和高衰减;BRS 预测速度频散和衰减在宏观流导致的弱频散和衰减基础上,同时体现出了介观波至流导致的低频高频散和低频高衰减以及微观喷射波至流导致的高频高频散和高衰减,能更好地在更宽频带范围内解释孔隙介质中波传播的频散和衰减现象.

2) 随着孔隙度的增加,波速整体减小,波衰减在频散过度带频带范围内增大;随着流体饱和度的增加,波速变小,代表介观流的衰减峰向高频方向移动,代表喷射流的衰减峰变化较小;包裹体尺度参数仅影响介观流,随着其增大,介观流波速频散过渡带和衰减峰向低频方向移动;随着渗透率的增加,波速和衰减曲线整体向高频方向移动.