车用滚珠式三叉杆万向联轴器热弹流润滑特性
2022-04-27胡德兴杨福芹耿春晖
胡德兴,杨福芹,耿春晖
(青岛科技大学 机电工程学院,山东 青岛 266061)
滚珠式三叉杆万向联轴器作为一种新型联轴器,主要由输入轴、三柱槽壳、滑块组件、三叉杆、输出轴组成。当联轴器工作时,3个滑块组件可以在滑块槽中滑动,滑块上嵌有数个滚珠,在滚珠与滑块槽配合面间形成纯滚动点接触摩擦副。该新型联轴器的破坏形式主要是在传递动力过程中,滚珠与滑块槽之间由于频繁的相对运动而产生的接触疲劳和磨损,因此本工作主要研究此处往复点接触的热弹流润滑问题。
近年来,已有学者对往复运动的弹流润滑问题开展了有益的研究工作。IZUMI等[1]对往复纯滚动点接触的油膜形成过程进行了光学干涉观测和数值分析。WANG等[2-3]利用光学干涉测量技术,对纯滚动短冲程及滑动往复运动下的点接触弹流润滑油膜分布进行了研究。SUDEEP等[4]研究了具有表面织构的点接触运动副在往复运动条件下的摩擦和振动行为。然而,这些工作都是关于往复运动弹流润滑的基础研究,没有与实际应用联系起来。
考虑到实际应用的复杂性,李栋等[5]在对滚动直线导轨进行运动分析的基础上建立了导轨副弹流润滑模型,并对其润滑性能进行了研究。李林林[6]对滚动直线导轨不同接触状态下的油膜润滑及动力学特性进行了研究。徐彩红[7]计算了往复运动齿轮齿条传动过程中的压力、膜厚、温度,获得了往复运动齿轮齿条的润滑状况。杨东亚等[8]基于弹性流体动压润滑理论建立了密封件弹流润滑计算模型和基本方程组,分析了活塞杆滑动速度对油膜厚度的影响。唐洪伟等[9]分别在静载荷和变载荷条件下分析了销轴与套筒往复运动工况下的线接触弹流润滑油膜变化情况。WANG等[10-12]研究了运动参数等对三叉杆万向联轴器线接触往复移动副润滑性能的影响。ZHOU等[13-14]对车用三叉杆滑移式万向联轴器的弹流脂润滑特性进行了探讨。
本研究将滚珠式三叉杆式万向联轴器用于某汽车传动轴,研究汽车各档位下联轴器的热弹流润滑特性,考察槽壳半径r、滚珠半径R、轴交角δ对热条件下弹流润滑膜厚、压力及温升的影响,以期对联轴器的改进及推广应用提供参考。
1 润滑模型与计算方程
1.1 联轴器弹流润滑模型的建立
图1(a)为滚珠式三叉杆式万向联轴器装配体,图1(b)为滚珠式滑块组件。
联轴器工作原理为输入轴转动,3个滑块组件相对于三柱槽壳和三叉杆往复移动,从而把运动和动力传递给了输出轴。

图1 滚珠式三叉杆万向联轴器Fig.1 Ball-type tripod sliding universal coupling
滑块组件在三柱槽壳内的相对速度方程[15]为

式(1)中,us为相对速度,m·s-1;r为槽壳半径,m;δ为轴交角;φo为输出角,φi为输入角,φo=φi。
假设滑块组件侧面的滚珠与三柱槽壳之间为均匀的球体与平面之间的点接触,则三柱槽壳施加到滑块组件上的力[15]为

式(2)中,M表示联轴器传递的转矩,N·m。
每个球体与平面之间的载荷为

式(3)中,N表示滚珠数量。
选取其中一个滚珠与三柱槽壳平面,建立如图2所示的等效点接触弹流润滑模型。其中,Rx、Ry分别表示滚珠在x方向和y方向的曲率半径,而平面的曲率半径近似看成无限大,故当量曲率半径R=Rx=Ry。研究[16]表明,联轴器在1/4周期处,滑块组件位于行程中点,由式(1)可以看出,此处速度最大,润滑特性最为典型且挤压效应不明显,故本研究基于图2分析研究联轴器运转1/4周期时单个滚珠运动到行程中点处与三柱槽壳的点接触热弹流润滑特性。

图2 等效点接触弹流润滑模型Fig.2 Equivalent lubrication model
1.2 基本方程
基本Reynolds方程为

式(4)中,p为油膜压力,Pa;h为润滑油的油膜厚度,m;u为卷吸速度,m·s-1;η为黏度,Pa·s;ρ为润滑油的密度,kg·m-3。
Reynolds方程边界条件为

膜厚方程为

式(6)中,h0为刚体中心油膜厚度,等式右边第二、三项为初始间隙量,等式右边第四项表示弹性变形,其中,E′为两固体的综合弹性模量,单位为Pa,,E1和E2分别为滚道和滚子的弹性模量,单位为Pa;v1和v2分别为滚道和滚子的泊松比。
载荷方程:

能量方程[17]:

式(8)中,cρ为定压比热容,J·(kg·K)-1;K为润滑剂热传导系数,W·(m·K)-1;u和v分别为x和y方向的油膜流速,m·s-1。
上下两界面的边界条件分别为

式(9)~(10)中,c1、c2为上、下界面比热系数,J·(kg·K)-1;K、K1、K2分别为润滑剂以及上、下界面热传导系数,W·(m·K)-1;u1和u2分别为上下表面的相对速度,m·s-1;ρ1和ρ2分别为上下表面材料的密度,kg·m-3;s为滑滚比;T0为初始温度,K。
黏压-黏温[18]方程为

密压-密温方程[18]:

式(12)中,ρ0为环境温度下润滑油的密度,kg·m-3;D1为密温系数,K-1。
2 计算流程
首先通过运动学、动力学方程计算出相对速度、载荷、综合曲率半径、椭圆率等参数初值,采用多重网格法求解Reynolds方程,弹性变形采用多重网格积分法求解[19]。假定温度初值,运用步进法求解能量方程,运用逐列扫描法求解润滑油膜温度[20]。在求解过程中不断修正膜厚和压力数值,当达到计算精度即压力和载荷计算结果的相对误差小于10-4,温度误差小于5×10-4时,计算过程停止,输出膜厚、压力及温升。
输入参数在表1中列出,取最高层网格节点数为256,网格层数为5,其余参数包括:Xin=-1.5,Xout=1.5,Yin=-1.5,Yout=1.5,T0=303 K,c1=c2=470 J·(kg·K)-1,k1=k2=46 W·(m·K)-1,ρ1=ρ2=7 850 kg·m-3。

表1 输入参数Table 1 Input parameter
计算过程中,以某型号汽车行驶数据[21]作为参考,各档位参数如表2所示。取联轴器轴交角δ=10°,槽壳半径r=0.08 m,滚珠半径R=0.007 m,在档位5工况条件下计算得到的热弹流润滑计算结果如图3所示,后续为便于观察,均取(Y=0)截面处曲线图。

表2 档位参数Table 2 Gear parameter

图3 点接触热弹流计算结果Fig.3 Calculation results of point-contact TEHL
3 计算结果与讨论
分别对1档至5档下联轴器的热弹流润滑数值模型进行求解,分析槽壳半径r、滚珠半径R、轴交角δ等参数对联轴器热弹流润滑的影响。
3.1 槽壳半径r的影响
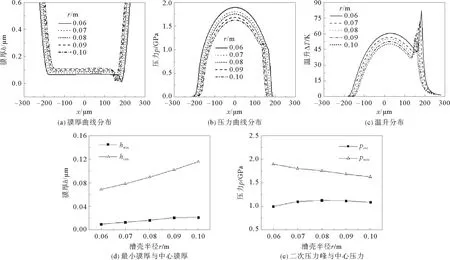
图4 槽壳半径r变化对热弹流润滑的影响(1档)Fig.4 Effect of groove shell radius r on TEHL(1st gear)
取滚珠半径R=0.007 m,轴交角δ=10°,槽壳半径r=0.06,0.07,0.08,0.09,0.10 m。图4为1档下槽壳半径r对联轴器热弹流润滑特性的影响曲线。观察图4(a)、4(b)可知,随着槽壳半径r增大,整体油膜厚度增大,油膜压力减小,润滑接触区宽度逐渐减小。尽管1档下联轴器的转矩T=785.3 N·m,转速n=280 r·min-1保持不变,但槽壳半径r增大时,滚珠与三柱槽之间的相对运动速度会增大,即润滑剂卷吸速度变大,而滚珠与三柱槽之间的作用力会减小,因此,膜厚逐渐增加而压力逐渐降低。由图4(c)的温升曲线可知,槽壳半径r越大,油膜温升就越小。
由图4(d)可知,随着槽壳半径r由0.06 m增至0.10 m,最小膜厚与中心膜厚都呈现出增大的趋势,但最小膜厚的增速相对较慢。图4(e)中,中心压力是单调下降的,但二次压力峰先是在槽壳半径r=0.08 m时上升到最大,随后缓慢下降。
2档至5档的计算结果汇总在表3及表4中。表3为不同槽壳半径r下油膜厚度及压力的计算值,表4为不同槽壳半径r下油膜温升的计算值。表3和表4表明随着槽壳半径r逐渐增大,2~5档下联轴器中除了二次压力峰表现出不规则的上下波动外,最小膜厚以及中心膜厚均增大,中心压力、中心温升及温升峰则逐渐减小,这与1档下滚珠与三柱槽壳之间弹流润滑特性的变化规律是一致的。
由此可见,在任一档位下,增大槽壳半径r可以明显增大油膜厚度,减小油膜压力,降低油膜温升,这有利于改善联轴器的热弹流润滑状况。虽然改变槽壳半径r对二次压力峰的影响程度并不明显,但也不能忽视润滑过程中二次压力峰的存在。

表4 槽壳半径r变化对油膜温升的影响(2~5档)Table 4 Effect of groove shell radius r on temperature rise(2nd—5th gear)
3.2 滚珠半径R的影响
取槽壳半径r=0.08 m,轴交角δ=10°,R=0.006 0,0.006 5,0.007 0,0.007 5,0.008 0 m。
图5给出了1档下滚珠半径R对联轴器热弹流润滑特性的影响曲线。由图5(a)、5(b)可知,当滚珠半径R增大时,油膜厚度整体小幅上涨,油膜压力则出现明显的下降,同时接触区宽度逐渐增大。这是因为尽管1档下联轴器的转矩M=785.3 N·m,转速n=280 r·min-1保持不变,使得滚珠与三柱槽壳之间的相互作用力不变,但滚珠半径R越大,滚珠与三柱槽壳之间的赫兹接触半宽就越大,单位面积的润滑油所承受的载荷就越小,故润滑油膜所承受的压力减小,膜厚增加。与此同时,油膜中心温升及温升峰明显减小,如图5(c)所示。

图5 滚珠半径R变化对热弹流润滑的影响(1档)Fig.5 Effect of ball radius r on TEHL(1st gear)
如图5(d)所示,随着滚珠半径R逐渐增大,最小膜厚与中心膜厚均呈现出线性增大的趋势。图5(e)展示了二次压力峰及中心压力的变化,当滚珠半径R增大时,二次压力峰与中心压力均呈现出明显的线性减小的趋势。
2档至5档的计算结果汇总在表5及表6中,其中,表5为不同滚珠半径R下油膜厚度及压力的计算值,表6为不同滚珠半径R下油膜温升的计算值。表5和表6表明随着滚珠半径R逐渐增大,2~5档下联轴器中除了二次压力峰表现出不规则的上下波动外,最小膜厚以及中心膜厚均增大,中心压力、中心温升及温升峰则逐渐减小,这与1档下滚珠与三柱槽壳之间弹流润滑特性的变化规律是一致的。
显然,任一档位下增加滚珠半径R对改善联轴器润滑状况是有利的,虽然膜厚值上升不明显,但油膜压力及温升都显著降低。但需要注意的是若一味追求较大的滚珠半径则必然要减少滚珠数量,这将导致单个滚珠所承担的载荷急剧增大而不利于润滑状况的改善。

表5 滚珠半径R变化对膜厚及压力影响(2~5档)Table 5 Effect of ball radius R on film thickness and pressure(2nd—5th gear)

表6 滚珠半径R变化对油膜温升的影响(2~5档)Table 6 Effect of ball radius R on temperature rise(2nd—5th gear)
3.3 轴交角δ的影响
取槽壳半径r=0.08 m,滚珠半径R=0.007 0 m,轴交角δ=6°,8°,10°,12°,14°。图6为1档下轴交角δ对联轴器热弹流润滑特性的影响曲线。从图6(a)可知,随着轴交角不断增大,油膜厚度呈现出明显的上升趋势,反观图6(b)中,由于增大轴交角对滚珠所受单位载荷的影响很小,故油膜中心压力并没有发生明显变化,但二次压力峰的则呈现出逐渐增大的趋势。根据图6(c)可知,改变轴交角对油膜温升整体的影响较为明显,随着轴交角δ增大,油膜温升明显增大,温升分布曲线逐渐向外扩大。

图6 轴交角δ变化对热弹流润滑的影响(1档)Fig.6 Effect of shaft angleδon TEHL(1st gear)
由图6(d)可知,在轴交角δ由6°递增至14°的过程中,最小膜厚与中心膜厚均明显增长,且中心膜厚的增速要明显快于最小膜厚,两者之间的差值不断变大。观察图6(e)可以发现,当轴交角δ变化时,油膜中心压力变化不明显。相反,随着轴交角δ增大,二次压力峰以较快的速度逐渐增大,当轴交角增大至10°时,增速开始放缓。分析上述现象出现的原因可能是,轴交角δ越大,润滑剂的卷吸速度越大,单位时间内在出口区积聚的润滑剂含量就越多而难以及时排除,导致二次压力峰增长越明显。当卷吸速度升高到一定水平时,油膜温升对润滑剂黏度以及金属弹性变形产生了影响,一定程度缓解了润滑油在出口区颈缩处的积聚现象,因此二次压力峰的变化趋于平稳。
2档至5档的计算结果汇总在表7及表8中,表7为不同轴交角δ下油膜厚度及压力的计算值,表8为不同轴交角δ下油膜温升的计算值。表7和表8表明,随着轴交角δ逐渐增大,2~5档下联轴器中除了中心压力表现出小幅度不规则的上下波动外,最小膜厚、中心膜厚以及二次压力峰均增大,油膜的中心温升及温升峰也随轴交角δ的增大而增大。因此联轴器2~5档下滚珠与三柱槽壳之间弹流润滑特性随轴交角δ的变化规律是一致的。
虽然任一档位下油膜压力以及温升会随着轴交角δ增大而有一定程度的增加,但整体上油膜厚度的上升趋势是更加明显的,这有利于改善联轴器的润滑状况。滚珠式三叉杆万向联轴器是作为汽车半轴总成的内球笼来使用的,通常情况下联轴器轴交角δ的值并不大。当轴交角δ增大到一定数值时,二次压力峰增长趋于平稳,膜厚则始终处于较高水平。因此,即使在较大轴交角δ情况下,该联轴器内滚珠与滑块槽之间依旧可以形成有效的弹流润滑。
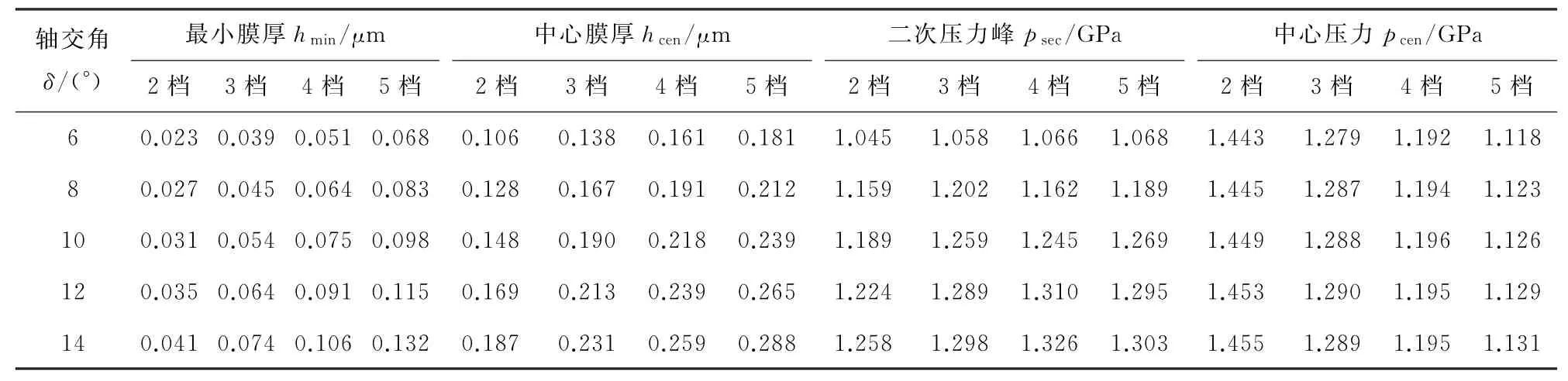
表7 轴交角δ变化对膜厚及压力影响(2~5档)Table 7 Effect of shaft angleδon film thickness and pressure(2nd—5th gear)

表8 轴交角δ变化对油膜温升的影响(2~5档)Table 8 Effect of shaft angleδon temperature rise(2nd—5th gear)
4 结 论
结合某型号汽车的实际行驶工况对滚珠式三叉杆万向联轴器滚珠与滑块槽之间的点接触摩擦副进行了热弹流润滑特性分析,结论如下:
1)任一档位下,增大联轴器的槽壳半径r、滚珠半径R均可以增大油膜厚度,降低油膜压力及温升,这有利于改善联轴器的润滑状况,实际使用中应适当选用较大的槽壳半径及滚珠半径。
2)任一档位下,增大联轴器轴交角δ虽然会使二次压力峰及温升逐渐增大,但油膜厚度的增长趋势更显著,这表明即便在轴交角较大的工况下,作为内球笼的滚珠式三叉杆万向联轴器依旧可以形成有效的弹流润滑。
