一种新型的塔康方位角估算方法

马雅男, 唐小峰, 邹 建, 徐 卫, 刘道煦

(成都天奥测控技术有限公司，四川 成都 611731)

塔康(Tactical Air Navigation System，TACAN)作为近程无线电导航系统，是飞机和航海的主要导航装备之一[1]，它通过距离和方位的测定，指示飞机出航和归航、沿路飞行及空中编队等。按照功能结构，塔康分为地面站和机载设备两部分，地面站发送一连串主基准脉冲、辅助基准脉冲、应答脉冲和随机脉冲等特征信号，机载设备通过对接收信号进行测量和分析，提取地面信标台的方位、斜距信息和台识别符号，进而实现极坐标定位[2-3]。目前塔康系统的信息收发主要采用模拟体质的构架[4]，其收发信号极易受到硬件、工艺、温度和环境的干扰，因此存在抗噪声能力差、定位精度低等问题[4-6]，严重影响了塔康测距和测位的性能。

传统的方位测量方法是通过测量信号包络正斜率过零点与基准脉冲之间的时间差，推导得到对应的方位角[1-3]，而噪声等因素会直接影响基准脉冲信号半幅测量点的定位和包络过零点的检测，进而影响测量精度。针对这一现象，中频数字化的概念在塔康方位估计中得到了广泛的应用[7-8]。为了提升方位测量精度，文献[9]采用离散脉冲信号直接进行曲线拟合得到包络信号，但是由于脉冲的占空比不均匀，因此拟合误差较大。随后，文献[10]利用了Kalman滤波原理提升了拟合曲线的精度，但是在大噪声下容易引发滤波发散，导致估计精度大幅下降。在此基础上，后人将压缩感知算法[11]、基于高程补偿的BLUE算法[12]、滑窗检测法[13]等多种技术应用于方位角估算过程中，均取得了满意的效果，但计算过程较为复杂，不易实现。

笔者提出了一种新型的塔康方位估算方法，该算法利用误差门限控制和拟合数据替换的方式对最小二乘模块输出的信号进行二次处理，剔除受噪声影响较严重的采样数据，采用满足门限要求的拟合信号进行替代，进而得到与基准信号更加符合的包络曲线，并在此基础上进行方位角的测算。为了证明新算法的有效性，将新算法与最小二乘法在相同信噪比下不同方位角的塔康系统中进行了对比仿真，随后增加了另一个维度相同方位角和不同信噪比下的仿真测试，测试结果表明利用新算法能够得到更精确的方位角信息，从而证明了算法的有效性和普适性。最后,通过FPGA在硬件板上进行了测试，新算法的实测结果优于最小二乘法的测试结果，进而反映出新算法的有效性，并具有较高的可实现性。

1 塔康信号方位测量原理

塔康系统采用相位式全向信标原理，机载设备通过接收地面站天线发射的具有方向性的信号进行参数计算实现测角功能。为了更精确地得到方位信息，塔康测角方式分为方位粗测和方位精测两个部分。为了达到这一目的，地面站发端发送的脉冲信号包括频率为15次/s的主基准脉冲群、频率为135次/s辅助基准脉冲群、识别脉冲群、均衡脉冲群和随机脉冲群等，该组合信号发出后受到15 Hz和135 Hz叠加正弦信号的包络调制[1]。方位粗测是在接收端通过测量15 Hz正弦信号的正斜率拐点与主基准脉冲的比相定时点，得到相位差值φ1。方位精测则需要解调得到135 Hz正弦信号的正斜率拐点与辅助基准脉冲的比相定时点，进而计算出相位差值φ2。在已知φ1和φ2的基础上，通过式(1)即可得到塔康系统的角度测量值φ,即

φ=40×⎣φ1/40」+φ2

(1)

2 基于最小二乘法的方位估算方法

塔康系统机载设备通过变频和滤波后，接收到的方位包络信号可表示为

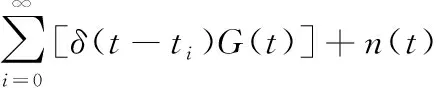
(2)

式中:U(t)为接收信号；Um为脉冲信号幅度；m1和m2为15 Hz和135 Hz包络信号的调制度；f1和f2分别为15 Hz和135 Hz；θ1和θ2分别为粗测角度和精测角度；G(t)为钟形调制信号；δ(t-ti)为编码器输出脉冲序列的任意脉冲；G(t)×δ(t-ti)为钟形脉冲编码序列，该序列包括主基准脉冲、辅助基准脉冲、识别脉冲、均衡脉冲、距离回答脉冲和随机填充脉冲；n(t)为接收的噪声。由于噪声的存在对接收端相位测量会产生一定的干扰，因为采用了延时-比较法[14]，主基准脉冲和辅助基准脉冲比相定时点受影响较小，但是15 Hz和135 Hz的包络信号则由于噪声的影响较难寻找正斜率拐点的位置。有无噪声存在下塔康接收的包络信号如图1所示。

图1 塔康包络信号示意图

由图1可知，与无噪声干扰时的基准信号相比并不平滑，存在一定的随机抖动，因此需要采用最小二乘算法对方位角进行有效的估计[15]。首先根据式(2)建立目标函数[15]：

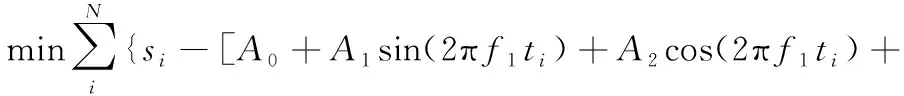
(3)

式中:si为接收端第i次采样数据;A1=A0×k1×cosφ1，A2=-A0×k1×sinφ1，A3=A0×k2×cosφ2，A4=-A0×k2×sinφ2，其中A0表征拟合曲线的幅度值，k1和k2为拟合曲线15 Hz和135 Hz包络信号的调制度，φ1、φ2分别为拟合曲线的粗测角度和精测角度。此时，记：

S=[s1,s2,…,sN]T

(4)

θ=[A0,A1,A2,A3,A4]T

(5)

(6)

将式(4)～式(6)带入式(3)，可得目标函数为

min(S-Hθ)T(S-Hθ)

(7)

为了得到目标函数的最小值对应的准确的矩阵θ，对式(7)进行求导，并令结果为零，可得：

θ=(HTH)-1HTS

(8)

利用式(8)得到的数据，提取参数，给出拟合曲线的粗测角和精测角为

φ1=arctan(A2/A1)

(9)

φ2=arctan(A4/A3)

(10)

将式(9)和式(10)带入式(1)得到最终检测角度。从上述过程可以看出，当接收信号矩阵S受到噪声影响较大时，会影响矩阵θ检测精度，从而导致方位角计算出现偏差，从而影响塔康系统定位的性能。

3 改进型的最小二乘法方位角估算方法

为了解决这一问题，在最小二乘法的基础上提出了一种新型的塔康方位角估算方法，其构架如图2所示。图2中，接收端包络信号[S1,S2，…，Sn]首先进入最小二乘计算模块，根据上面最小二乘法的描述按照采样时间对信号进行分集，表示为Mi(其中i表示分集个数，i=[1,2，…，k]，k为分集个数)，然后构造对应的基于时间的H(i,j)矩阵(其中j表示分集内的采样点个数)，计算得到每一个分集的θi。随后将得到的θi数据送入筛选单元，该单元将[θ1,θ2,…，θk]个数据按照升序或降序排列，去掉前15%和后15%个数据点，将位于中间的16%～85%个θi值做平均得到avg(θ)。

图2 塔康方位角估计算法构架

后续求得avg(θ)与每一个[θ1,θ2,…，θk]的绝对误差|avg(θ)-θi|，当误差小于设定的门限值时，则表示每一个θi都满足要求，[θ1,θ2,…，θk]序列输出送入求平均单元得到最终的角度值；当误差大于设定的门限值时，则代表该θi含有较大的误差，用avg(θ)将其替换输出至替换单元，该单元将θi对应的实际采样分集Mi的数据[Si,Si+1，…，Si+m]输入模块中，随后计算这些实际采样信号Sj(其中j表示采样点数，j=[i,i+1,…，i+m])与拟合得到的数据H(i,j)×avg(θ)之间的绝对误差|Sj-H(i,j)×avg(θ)|，当误差满足设定的门限范围内时，说明此时Sj符合要求，一旦误差超过门限时，则将H(i,j)×avg(θ)取代Sj输出至最小二乘模块中，并重新计算θi，循环往复，直至误差满足门限要求。

该方法利用大数据平均得到较为准确的avg(θ)，以该值为指引剔除噪声较大的采样值Sj，并以更准确的H(i,j)×avg(θ)作为替代，重新对θi进行计算，进而得到更精确的方位角。

4 仿真与分析

为了验证本文提出的方位角估计方法的正确性，利用MATLAB平台进行了仿真验证，并与最小二乘法的结果进行了对比，参数设置如表1所示。原始接收信号曲线、基准参考信号和经过改进型最小二乘估算法拟合信号如图3所示。

表1 塔康信号参数设置

根据表1的参数，利用图3中的接收信号根据最小二乘法计算矩阵θi，随后提取θi中与方位角计算有关的参数A2(i)和A1(i)及两项的平均值，得到A2(i)/A1(i)-avg(A2/A1)的误差曲线，如图4黑线所示，此时的误差范围在-0.6～0.5之间。为了减少误差干扰，新算法将±0.2之外的θi用avg(θ)取代，如图4红色线所示，此时误差曲线比最小二乘法对应的误差缩小了近1/3。

图3 接收信号、基准信号和新算法拟合信号

图4 新算法与最小二乘法的幅度误差

利用avg(θ)，重新逆向计算拟合信号H(i,j)×avg(θ)，随后将对应的采样信号与拟合信号相减，当小于门限0.8时保留该采样点，而当超过误差门限时，则用拟合信号(图3红色线)替代采样信号。可以看到，相比于接收采样信号，经过误差门限控制后的拟合信号中由噪声叠加引起的尖锐的峰值和谷值被剔除，转而由更接近基准参考信号的数据所替代。将图3中的接收信号与基准包络信号相减，得到的误差曲线如图5蓝色虚线所示，该曲线误差范围在[-4～4]之间。经过误差门限限制后的拟合曲线(图3红色线)与基准包络信号的误差曲线如图5红色实线所示，该误差范围为±3.5，小于采样信号误差。

图5 接收信号和新算法拟合信号与基准信号的误差曲线

在此基础上计算得到的方位角曲线如图6所示，为了对比方便，图6中同时给出了利用最小二乘法得到方位角曲线。图6中基准方位角(图6蓝色线)为表1设置的35°，利用最小二乘法计算的方位角曲线(图6黑色线)相较于基准方位角有了较大幅度的波动，误差范围在-24°～17°之间变化，而波动的原因主要是噪声的引入导致了角度计算的误差增加。为了降低这一误差，利用新算法得到方位角曲线，相比于最小二乘法曲线，其波动的幅度更小，误差控制在±9°之内，且大部分误差集中在±5°范围内。因此其方位角的计算均值为35.25°，相比于最小二乘法的结果35.79°，提升了0.54°，与基准值更加接近。

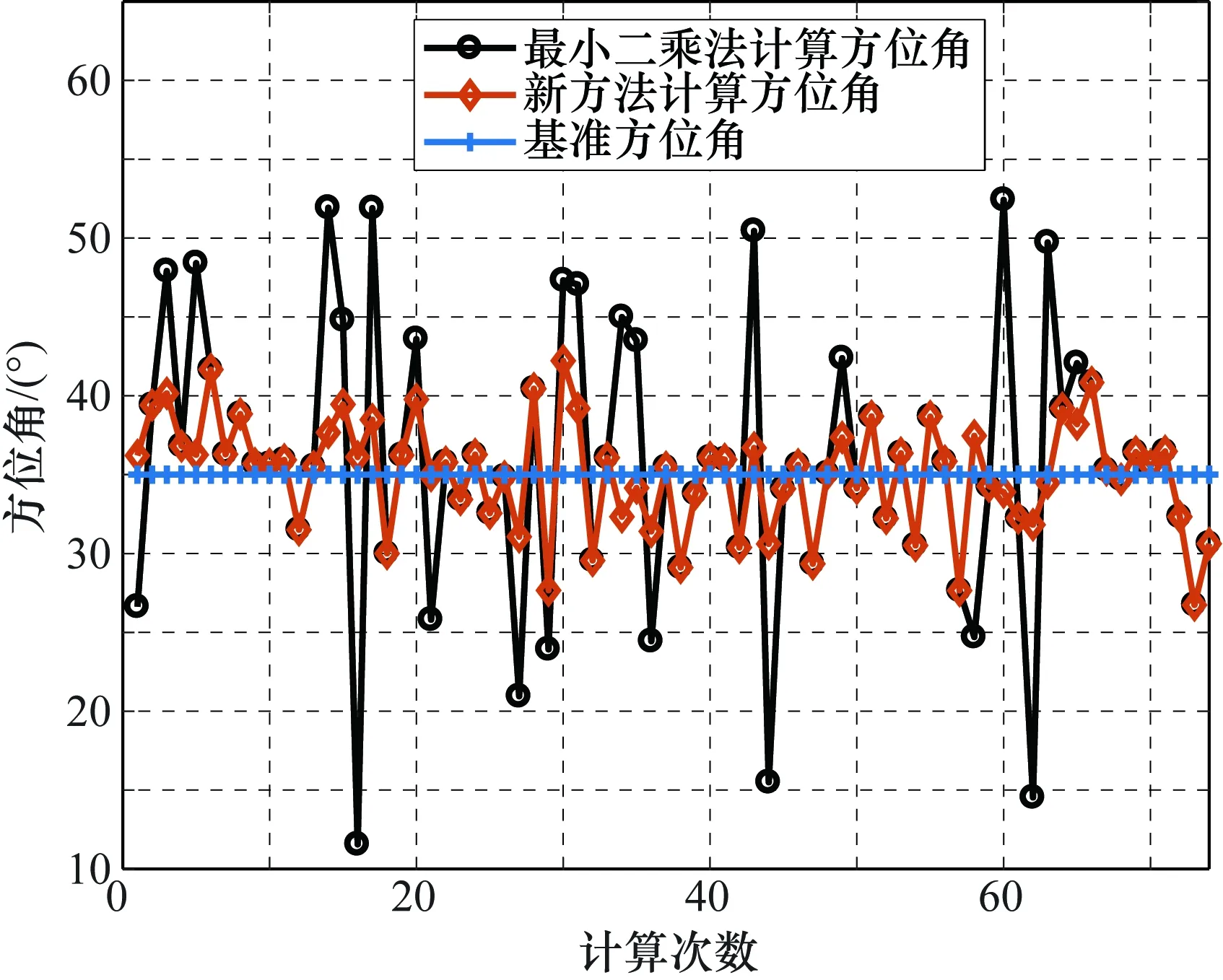
图6 新型估计方法与最小二乘法计算的方位角曲线

为了进一步证明算法的有效性，在SNR为23 dB的环境下，分别选取了4个象限的参考角度为35°、125°、215°和305°，然后利用最小二乘法和新算法进行测试，得到的结果如表2所示，测试结果与基准角的误差如图7所示。从图7和表2中都可以看出，与最小二乘法相比，新算法能够对每个测试角度进行优化，将误差由原来的[-0.25°～2°]，降低至±0.25°之内，因此这一结果证明了在塔康系统方位角计算过程中，针对任意角度，利用新型算法对抑制噪声干扰提升估算精度都是非常有效的。

表2 不同参考角下最小二乘法和新算法测试结果

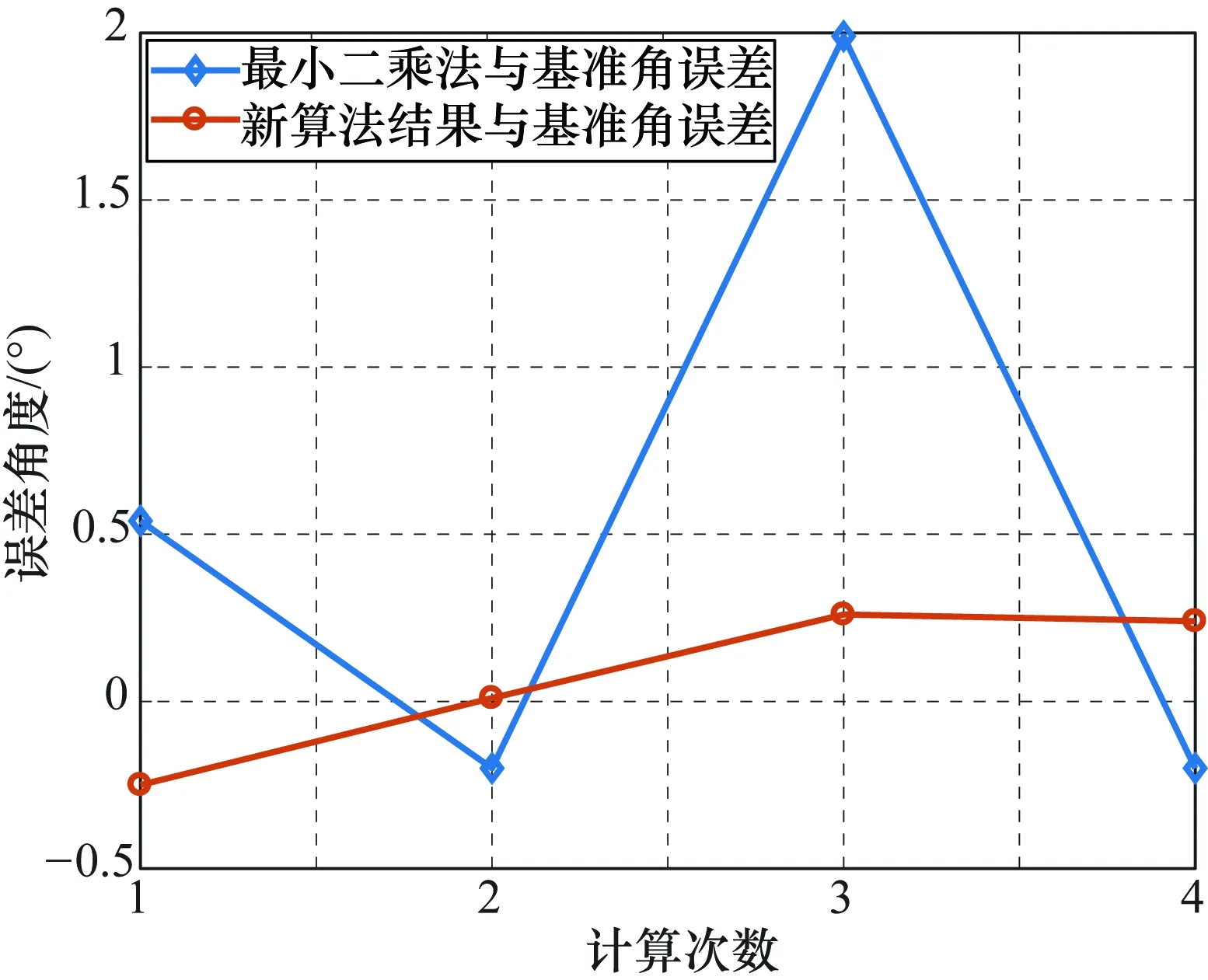
图7 塔康方位角估计算法结果

为了证明算法的普适性，又在方位角为35°的条件下，选取了13～38 dB(以5 dB为间隔)的6个SNR，利用最小二乘法和新算法分别进行方位角检测，得到的结果如图8所示。从图8中可以看出，利用新算法能够有效地将噪声等因素引入的误差降低至±0.6°之内，与最小二乘法的计算结果[-6°～0.9°]相比，测量精度提升了90%，因此证明了本算法具备优异的抗噪声能力，能够快速寻找并排除野值的影响，进一步优化系统的性能。

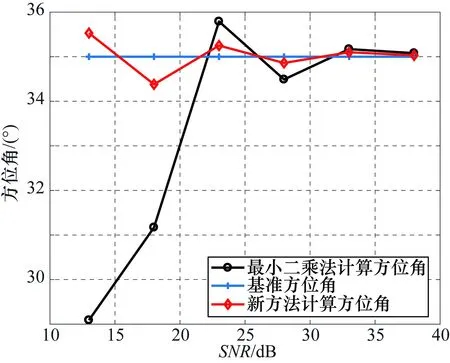
图8 塔康方位角估计算法结果

最后，为了进一步验证算法的有效性，搭建实验环境对算法进行测试验证，如图9所示，利用XC7Z045 FPGA芯片结合收发2路AD9361高速ADC芯片进行实验验证，设置基准方位角为80°，发端加载带有20 dB高斯白噪声的塔康信号进行发送，换回后收端经A/D采集接收，随后在FPGA芯片中分别利用最小二乘法和新算法对方位角进行计算。其测试结果如图10所示。设置的基准方位角为80°，由于噪声的影响，其最小二乘法测试得到的曲线(蓝色线)在基准方位角上下剧烈波动，浮动区间达到[67°～100°]之间，平均后测试结果为82.3°，相比于基准方位角误差达到了2.3°，测试精度无法达到预期要求。由于新算法用误差较小的数据取代了大误差数据，使得整体测试结果在[72°～87°]之间浮动，平均后得到的测量结果为79.3°，与基准角度相比误差仅为0.7°，比最小二乘法测试结果提升了1.6°，因此证明了新算法具有较好的抗噪声性能，并且具备可实现性，有助于提升系统的测试性能。

图9 实验测试环境

图10 基于FPGA的新算法与最小二乘法方位角曲线

5 结束语

针对噪声下的塔康系统，提出了一种新型的方位角计算方法并进行了仿真验证。该方法利用最小二乘法的思想，结合误差门限控制和拟合数据替换的方法，将大误差接收信号转换成更逼近实际基准包络的曲线，进而降低了噪声的影响，提升了方位角计算的精度。仿真结果表明，利用该算法能够在SNR为23 dB的情况下，有效地将塔康系统的方位角误差从0.79°降低至0.25°，在一定程度上降低了噪声的影响。随后针对不同的方位角和不同的信噪比环境，将该算法与最小二乘法结果进行对比，表明该算法能够将方位角测量精度提升10%～90%，进而有效地优化了系统的性能。最后，利用FPGA在硬件板上进行测试验证，新算法测试误差与最小二乘法相比提升了1.6°，进而证明了新算法设计的有效性和可实现性。