基于遗传优化混合模型发动机稳态数据融合
2022-04-27白楚枫杜建红朱赤洲
哈 圣, 白楚枫, 杜建红, 朱赤洲, 姜 华
(中国航发沈阳发动机研究所,辽宁 沈阳 110015)
航空发动机稳态数据受实际复杂工况影响,数据本身会具有一定的非定常性。受测量方式、工作环境、控制规律等多方面因素影响,稳态数据本身将存在噪声,有时甚至存在一定的漂移[1-3]。随着我国发动机试验测试能力的提升,数据采集能力也有了较为显著的提高,往往试验过程中稳态数据样本点数量在上千量级。随着试验考核项内容的不同,稳态数据样本空间成倍增长,使得噪声数据的数量也随之增长。传统的数据噪声剔除与融合方法大多适用于小样本空间,且数据分布特性基于单一正态分布特性假设[1,4],这类方法本身很难保证数据得到充分利用,且在时间尺度增加致使样本空间加大时很难保证稳态数据样本符合单一分布特性。航空发动机稳态数据在大样本空间下的数据筛选便成为一个难题。
近些年,随着人工智能的兴起,国内外逐渐开始使用一些智能分类算法进行数据筛选,例如K-means聚类算法[5-6]、LOF检测算法[7]等方法。文献[8]中指出,K-means算法自20世纪60年代以来经Bradley与Berkhin等改进后,算法本身收敛速度得以提升并扩展到了分布式聚类领域,使其成为一种应用较广、较为高效的聚类方法,在数据异常值剔除方面有着较为广泛的应用。但此类方法依托闵可夫斯基距离,很难表征测量数据的分布特性和样本概率。为了能够尽可能地表征稳态数据本身的分布特性,考虑到小样本空间的数据正态性假设[4],将其拓展至大样本空间,采取高斯混合模型进行数据分类,从而筛选数据,并利用混合模型本身良好的回归特性表征数据的概率特性。
目前,常见的高斯混合模型求解方法为期望极大(Exceptation Maximization,EM)算法[9-10],该算法因计算简便得到了广泛应用,但算法本身仅具有局部收敛特性,工程上往往采取多次计算,选择最佳回归解作为最终结果。为此,本文采用遗传算法对EM算法进行优化,利用遗传算法并行搜索得到模型求解结果全局最优。基于高斯混合模型求解结果筛选有效数据并将模型参数进行融合得到反映该稳定状态的特征参数值。
1 混合模型
混合模型作为统计学的一类重要模型,被广泛应用于生物、金融、地质统计和社会科学等诸多领域。根据模型组合形式分为线性混合模型与非线性混合模型。线性混合模型中的子单元模型构造类型不同分为高斯混合模型、狄利克雷混合模型等。
根据文献[4]、文献[11]和文献[12]可知,因发动机稳态数据采用等精度传感器测量,并且在航空发动机试验过程中测量形式符合中心极限定理使用情况,可认为发动机稳态数据基本符合正态分布特性,因此采用高斯混合模型作为数据分类模型,其概率分布为
(1)
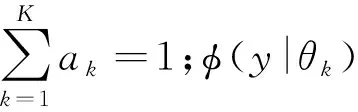
2 遗传优化求解算法
对于高斯混合模型,工程上常采用EM算法求解,但该算法所得近似解本身仅具备局部最优。遗传算法是一种模拟生物在自然环境中的遗传和进化过程的自适应全局优化搜索算法。该算法因具有高效、实用、强鲁棒性被广泛应用于机器学习、模式识别、神经网络、控制系统优化等多个领域[13]。在全局优化问题上,遗传算法通过对当前种群施加选择、交叉和变异等一系列遗传操作,产生新的种群,并逐步使种群进化至群体最优,达到求解近似最优解的目的。因此,可利用该算法的全局搜索特点,求解高斯混合模型全局最优解。
2.1 遗传算法适应度函数
2.2 GA-EM混合优化算法
遗传算法虽然具有较强的全局收敛特性,但算法本身对局部搜索能力较差,这与算法本身的变异、交叉、择优方式选择相关。因此,为了增强算法局部搜索能力,且弥补遗传算法因保证计算结果精度所带来的迭代时间延长,将EM算法作为遗传算法的补充算法,采用遗传算法与EM算法的混合优化EM算法。EM算法在每次迭代过程中分为:E步,求解模型期望值;M步,求解模型极大似然估计值[14]。
具体求解过程如下。
① 给定分模型数量K,提取样本数量为N的稳态数据样本。
② 遗传算法求解模型参数,得到粗略模型参数值。
③ E步,依据当前模型参数,计算分模型k对观测数据yj响应度:
(2)
④ M步,计算新一轮迭代模型参数:
(3)
(4)
(5)
3 稳态数据融合方法
通过高斯混合模型对稳态样本数据进行数据筛选,可以得到不同划分数量以及当前模型参数下样本统计特性。为防止高斯混合模型在使用过程中出现样本数据的“过拟合”和“欠拟合”现象,选择AIC信息准则[15-16]和BIC信息准则[17]作为混合模型回归最优解的评判标准。具体计算方法为
AIC=2K-2lnL
(6)
BIC=KlnN-2lnL
(7)
式中:K为模型参数个数;L为模型极大似然函数值;N为样本数量。
由于发动机试验过程中稳态参数数据特性受控制规律、工作环境和测量设备特性影响,数据本身时不变性随采集时间增长,数据波动性愈发显现,部分参数存在温漂、时漂的现象较为明显。随着采集时间增长,样本空间中数据本身不再满足单一正态分布。从时间域来看,可将数据视为由若干正态分布稳定工作点数据与噪声混合叠加构成,波动性表现为若干稳定工作点间的数值切换。
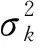
通过选取经高斯混合模型筛选过的方差水平接近合理量级的分模型均值,对均值所划分模型权重做加权平均即可得到稳态数据融合特征。具体算法为
(8)
式中:m为筛选方差后合理量级分模型总个数。
因为BIC信息准相较AIC信息准则而言,采用KlnN代替2K,在大样本空间中较AIC数值低,具有更高的稳定性。充分利用AIC与BIC在不同样本空间的适应性,采取对小样本空间使用AIC值作为评判模型最优化参数、对大样本空间使用BIC值作为模型最优化参数的方法。整个计算过程包括高斯混合模型求解、模型最优化形式确定和最优化模型参数特征值融合,具体计算过程如图1所示。

图1 稳态数据融合过程图
4 仿真对比与实验数据验证
4.1 仿真样本选择
为了验证GA-EM混合优化算法较遗传算法收敛速度提升,以及采用AIC/BIC信息准则后数据筛选结果准确性提高,使用样本数据为300个N(600,5)、400个N(570,3)和300个N(610,7)作为稳态基本数据。为模拟发动机试验过程中测量的数据噪声,分别对稳态基本数据添加一定比例正弦与脉冲噪声,添加后数据形式如图2所示。

图2 仿真数据折线图
图2中折线1为在稳态基本数据基础上添加的脉冲信号,折线3、折线5分别为添加的10sin(300t)+15、40sin(300t)噪声,其余折线为上述原始模拟样本数据。
4.2 遗传算法求解结果
使用遗传算法求解在图2样本数据下高斯混合模型,经计算高斯混合模型在[2,10]区间取整数时,经EM算法多次计算确定分模型个数为8时BIC值最小。遗传算法选定种群规模为20,交配概率为0.8,变异概率为0.2,收敛标准选定为超过连续代数不进化,用StallGenLimit表示,其值分别设为50,100,150,200,400,600,800,1000,根据BIC值判定模型求解结果优劣,计算结果如表1所示。
由表1结果可知,遗传算法作为一种启发式搜索算法,其计算结果稳定性很难保证,算法本身受种群规模、交配率、变异率、适应度函数选取影响,一般为了使结果更加准确会选择增加种群规模的方式提升样本的多样性。因此,本节增加种群规模至50,StallGenLimit设为1000,计算过程如图3所示,样本数据的分类结果如表2所示。
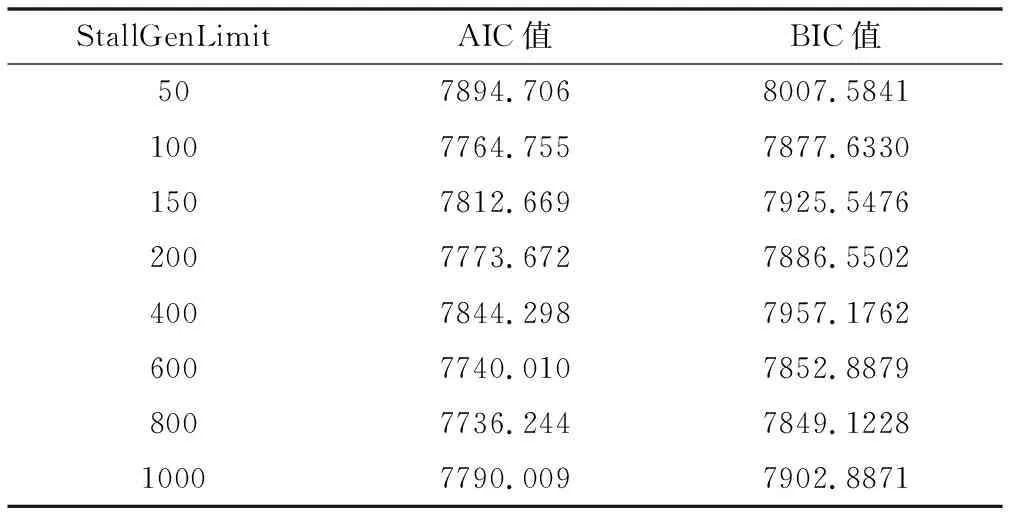
表1 不同StallGenLimit遗传算法计算结果(种群规模=20)
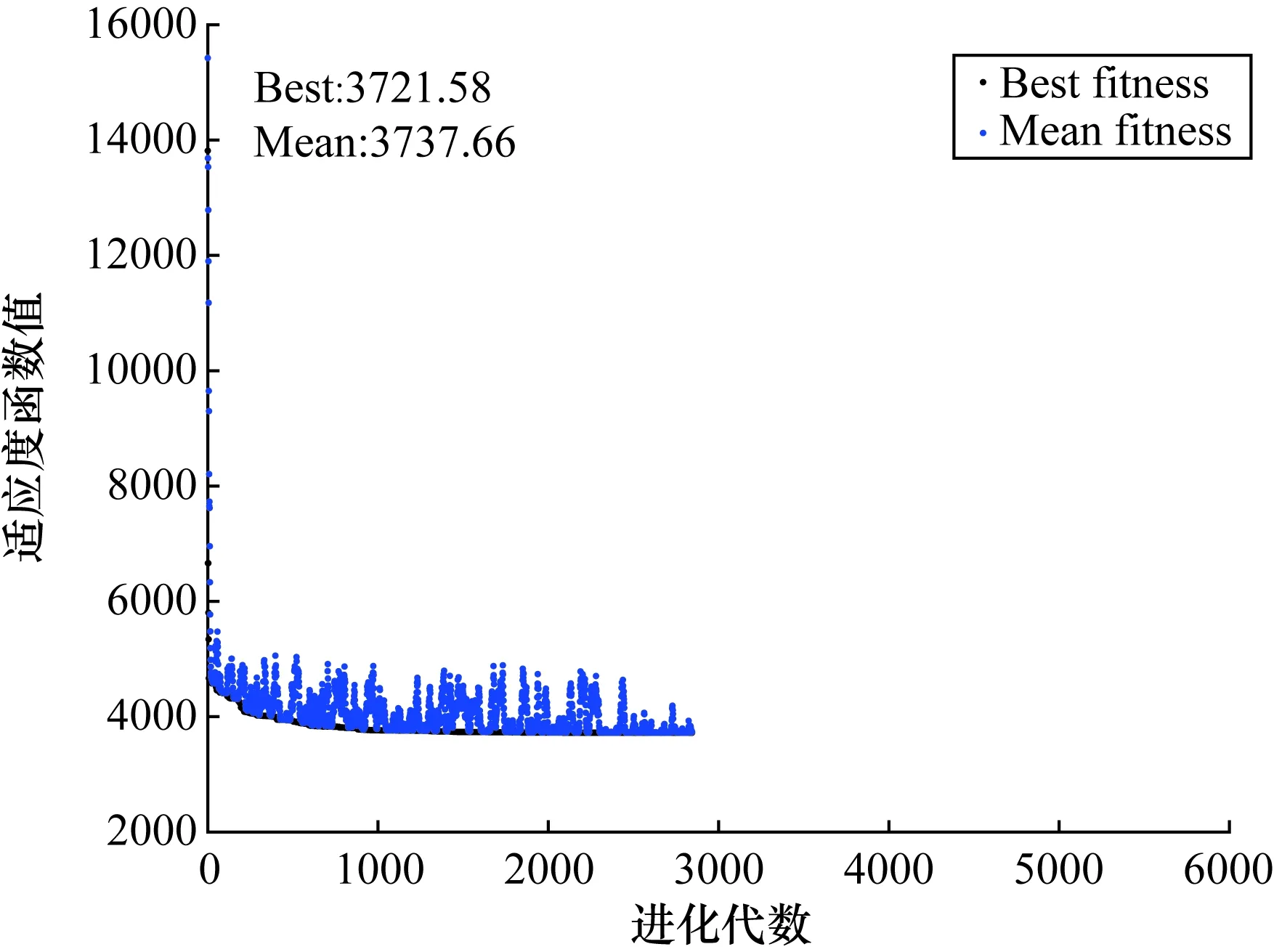
图3 种群规模=50,StallGenLimit=1000计算过程图
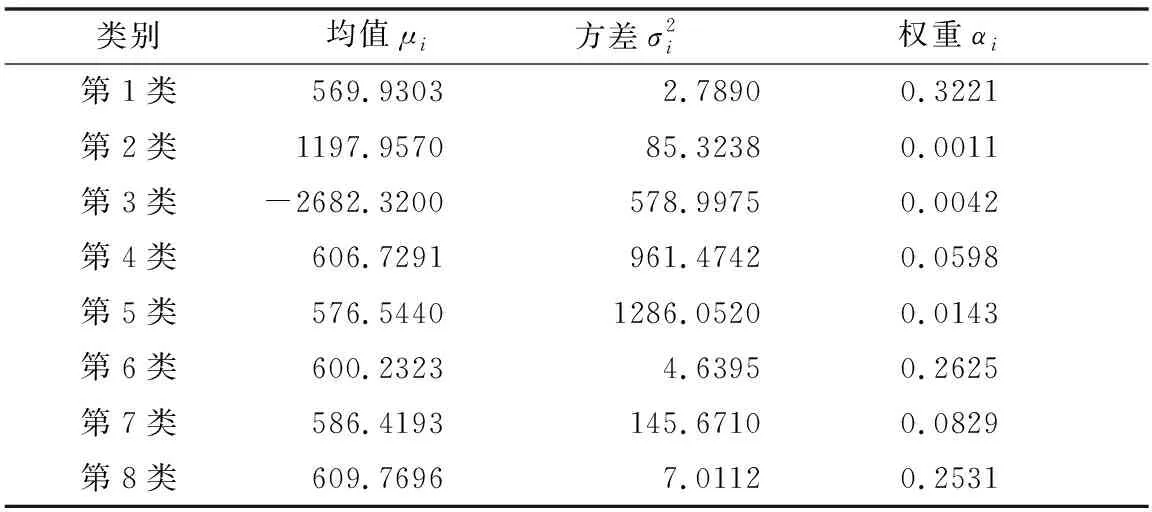
表2 计算结果(种群规模=50,StallGenLimit=1000)
将表2计算结果与仿真样本数据进行对比发现,根据方差与数据权重筛选可求得高斯混合模型的稳态基本数据的近似解为N(569.9303,2.7890)、N(609.7696,7.0112)、N(600.2323,4.6395),且AIC与BIC值分别为7623.123与7736.001。根据式(8)所得数据融合特征值为591.4626,与仿真数据稳态基本数据融合后的特征值591.7143相比,相对误差为0.04%。
4.3 GA-EM优化算法求解结果验证
考虑算法局部收敛对初始值选择的敏感性,将StallGenLimit设为100,作为遗传算法的收敛标准,选定种群规模为20,交配概率为0.8,变异概率为0.2。按照2.2节中算法进行求解高斯混合模型,求解结果如表3所示,数据分类效果图如图3所示。
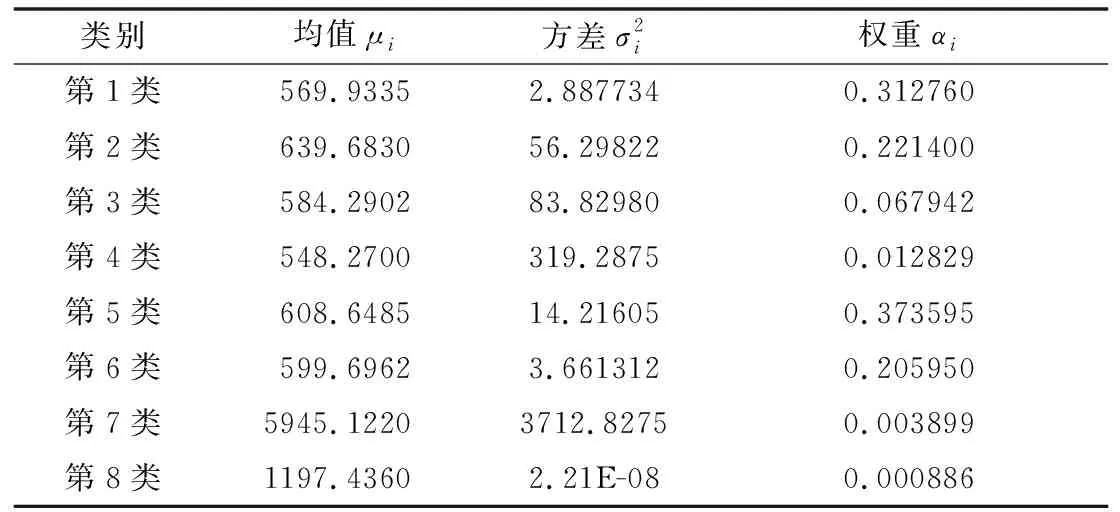
表3 GA-EM优化算法求解模型结果

图4 数据分类效果图
根据数据分布相似性原则和权重可知筛选出稳态基本数据近似解为N(569.9335,2.887734)、N(609.6485,14.21605)、N(599.6962,3.661312),且AIC与BIC值分别为7617.5367与7730.415。根据式(8)所得数据融合特征值为593.0123,与仿真数据稳态基本数据融合后的特征值591.7143相比,相对误差为0.22%。
4.4 试验数据验证与应用
选取某型号发动机试验过程中的某段推力稳态片段数据作为验证数据。因测量故障原因,该数据片段存在噪声,且信噪比较大,波动量明显。为方便描述,对推力数据进行归一化处理。经GA-EM求解后BIC最优的模型分类结果如图5所示。
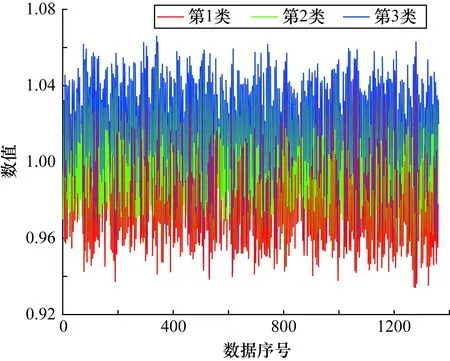
图5 推力稳态片段分类结果
通过对比以往推力数据,根据分布相似理论选择第1类、第3类作为稳态基本数据,其均值近似解按权重融合后为1.0058,进行大气环境修正的换算推力归一化结果为1.0119。将该结果与同一批次该发动机无测量故障数据对比,在同状态下按低压换算转速插值得到大气环境修正后的归一化结果为1.0101。
5 结论
本文基于测量数据正态性假设,使用高斯混合模型对稳态数据进行筛选,并对数据筛选结果进行数据融合。通过仿真对比与试验数据验证结果表明:
① 遗传算法求解的模型速度较慢,且参数变量较多,对算法结果稳定性影响较大,采用GA-EM算法可加快收敛速度且算法计算结果相对稳定。
② 使用AIC/BIC作为数据筛选结果最优准则,可有效划分数据类别。
③ 通过模型求解参数按照数据分布相似原则,对数据进行融合可得到较为准确的稳态参数特征值。
该方法对正态分布样本或近似正态分布样本数据进行筛选分类,通过权重和分布相似性原理进行数据筛选。但收敛速度主要受遗传算法影响较大,而且EM算法初始值对遗传算法计算结果较为敏感,虽然可以循环迭代使用GA-EM提升结果的准确性与稳定性,但仍需对遗传算法进行改良,以加快收敛速度。
