基于MatDEM的三维实际地形尾矿库溃坝数值模拟
2022-04-27吕松峰张慧颖王新华武文浩陈泳江
吕松峰,张慧颖,王新华,武文浩,陈泳江
(云南农业大学水利学院,云南 昆明 650201)
尾矿库用于贮存矿石选别尾矿,通常位于高势能的山地之间,由筑坝或圈地建成,是具有高势能的危险源。引起尾矿库溃坝的原因主要有洪水漫顶、渗透破坏、地震作用和坝基破坏等。尾矿库溃坝,会对下游居民的人身财产安全造成不可估量的损失。
模型试验是研究尾矿库溃坝机理的一种非常重要的方法;但模型试验存在缩尺效应、费用昂贵、耗时长等缺点,难以全面推广。数值模拟方法可以清晰明了地显示尾砂流在溃坝过程中的状态,同时也有助于节约科研成本。陈俊等建立了耦合数学模型并模拟了水槽溃坝试验,证明了数学模型能够准确地计算三维溃坝流沙运动[1]。阮德修等基于FLO2D与3DMine耦合的数值模拟,得到了三维动态反演尾矿库溃坝泥沙流实时灾害过程,为灾害数字化评价提供了新途径[2]。尹光志等通过研究相似模型,得到了尾矿坝溃坝后泥浆流动的特性[3]。杨蓉等基于Fluent软件对三维实际地形下的尾矿库溃坝数值模拟研究,能够充分考虑模拟区域地形特征对尾矿库溃坝尾砂浆运动的阻滞、拦截作用,反映不同地形下尾矿库溃坝泥沙流的运动特性[4]。李火坤等基于FLOW-3D软件建立三维数值模型,很好地模拟了出水流的自由液面流动现象并准确计算出其流场性质[5]。这些研究虽考虑尾矿库溃坝是一种流固体结合的溃坝,但尾矿库溃坝数值模拟大多采用有限元的方法,导致研究结果具有局限性。
由于溃坝原因复杂,笔者考虑了尾沙流单元体间的内摩擦力,利用离散元软件MatDEM模拟尾矿库在瞬时局部溃坝情况下的尾砂流速度及其淹没情况。
1 颗粒流离散元法的基本原理
离散元法[6]是通过堆积与胶结具有力学性质的单元体来建立模型,并在此基础上利用时间步迭代算法来进行数值模拟。
1.1 单元接触模型
在最基本的线性模型中,假定颗粒之间靠弹簧相互接触和产生力的作用[7]5。线弹性模型如图1所示。通常来说,为了防止破坏发生,颗粒之间的法向力(Fn)、法向变形(Xn)、剪切力与剪切变形应满足公式(1)[8]:
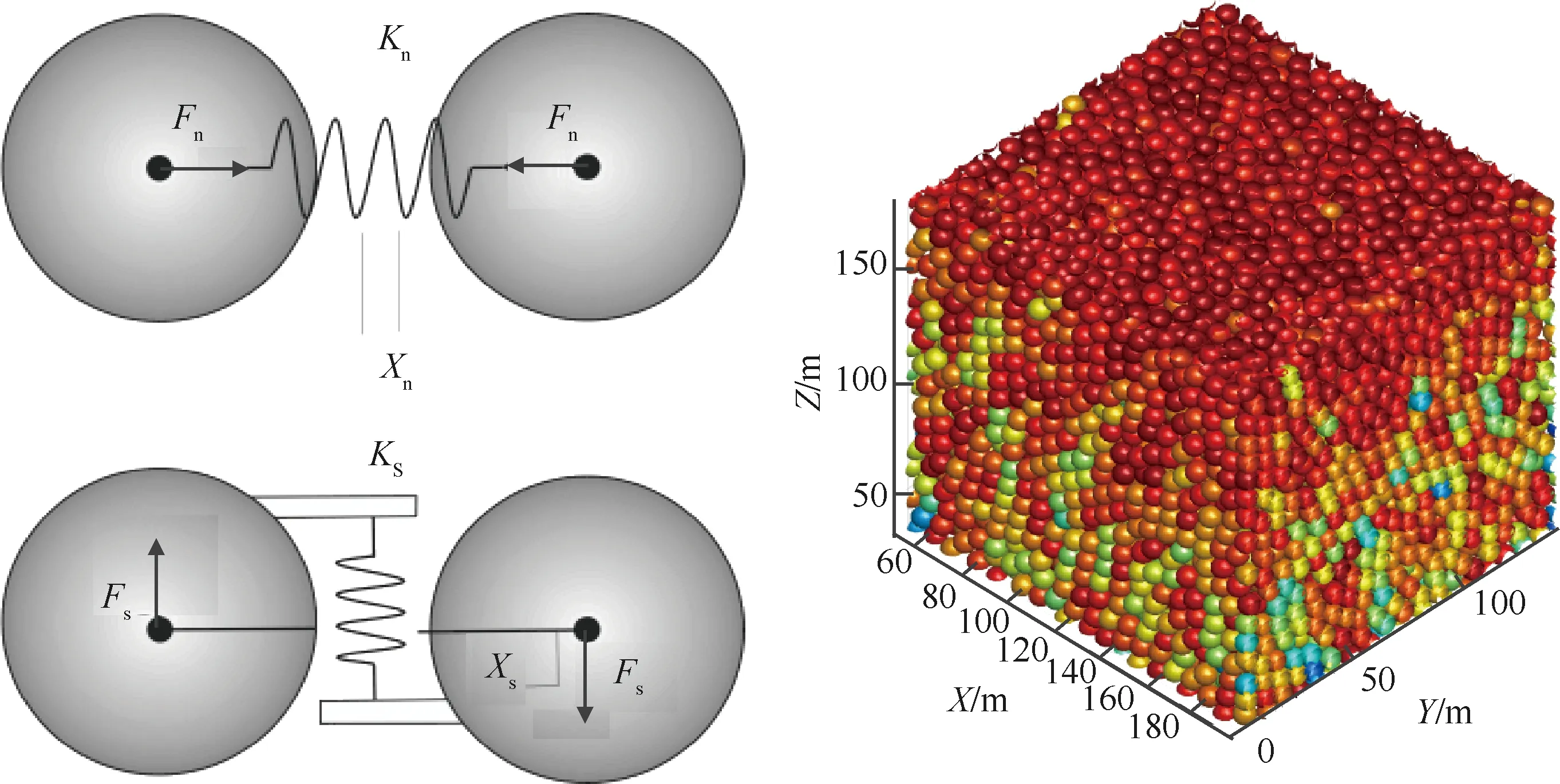
图1 线弹性模型示意图
(1)
式中:Fn—法向力,N;Kn—法向刚度,N/m;Xn—法向相对位移,m;Xb—断裂位移,m。
初始时,颗粒与其相邻颗粒相互连接,受拉力或压力作用。当两颗粒之间的Xn大于Xb时,弹簧断裂,颗粒间拉力消失。
通过切向弹簧来模拟颗粒间的切向力(Fs)和剪切变形(Xs),计算公式为
Fs=KsXs,
(2)
式中:Fs—颗粒间的切向力,N;Ks—切向刚度,N/m;Xs—切向相对位移,m。
同样地,弹簧在切向上的破坏基于摩尔-库仑准则[7]6
Fsmax=Fs0-μpFs,
(3)
式中:Fsmax—最大抗剪力,N;Fs0—颗粒间的初始抗剪力,N;μp—颗粒间的摩擦系数。
在摩尔-库仑准则里,相邻颗粒之间的最大抗剪力与初始抗剪力(Fs0)相关。Fs0为相邻颗粒间在没有施加法向压力时能承受的最大剪切力,类似于岩土体的黏聚力。Fn越大,Fs0也越大。当F超过Fsmax的时候,切向连接消失,此时相邻颗粒之间只有滑动摩擦力-μpFs。
1.2 两种不同单元的连接
研究涉及2种不同单元间(水粒子单元和尾矿砂粒子单元)的连接,所以给出不同单元连接的等效法向刚度。
对于法向刚度为Kn1和Kn2的2个单元,其连接的等效法向刚度(Kn)为
(4)
对于切向刚度为Ks1和Ks2的2个单元,其连接的等效切向刚度(Ks)为
(5)
式中:Kn—等效法向刚度,N/m;Kn1—水粒子单元法向刚度,N/m;Kn2—尾矿砂粒子单元法向刚度,N/m;Ks—等效切向刚度,N/m;Ks1—水粒子单元切线刚度,N/m;Ks2—尾矿砂粒子单元切线刚度,N/m。
1.3 MatDEM离散元法计算流程
MatDEM软件具有计算效率强、力学性质明确、可以二次开发等优点,可利用其进行尾矿库溃坝数值模拟研究。本研究分以下几步。
1.3.1 进行尾矿库模型堆积
根据尾矿库溃坝的影响范围,设定1个符合实际地形的数值模拟箱,在箱中堆积满单元颗粒。通过模拟重力,得到符合自然堆积的初始底层堆积模型。
1.3.2 根据尾矿库的具体尺寸确定尾矿库模型体
根据尾矿库的具体尺寸(长180 m、宽100 m、初期坝高程2 450 m、堆积坝高程2 550 m),利用过滤器削平堆积底层。为了得到符合实际形状的尾矿库模型体,需要利用过滤器将堆积模型中的部分颗粒剔除,其中用到了MatDEM软件中的布尔矩阵topLayer Filter。
1.3.3 材料设置
根据材料的不同,设置2个不同单元组进行模型的胶结平衡。本模拟的尾矿库水砂粒子比为1∶3。
1.3.4 平衡迭代计算
尾矿库尾砂在自身重力影响下通过溃口发生溃坝,利用MatDEM软件进行平衡迭代计算,在溃坝的过程中记录尾砂的速度。
颗粒间的5个力学参数(Kn、Ks、Xb、Fs0、μp)由材料的5个宏观力学性质通过转换公式计算得到。这5个宏观力学性质为杨氏模量(E)、泊松比(ν)、抗压强度(Cu)、抗拉强度(Tu)与内摩擦系数(μi)。具体转换公式为[9]
(6)
(7)
(8)
(9)
(10)
(11)
式中:d—颗粒直径,m;I—比例系数;E—杨氏模量,GPa;ν—泊松比;Tu—抗拉强度,MPa;μp—摩擦系数;Cu—抗压强度,MPa;μi—内摩擦系数;
获得参数具体步骤:1)将现场获取的尾砂材料通过室内试验得到宏观的5个力学性质;2)通过三维转换公式求得颗粒间5个力学参数关系;3)运行MatDEM软件中自有的杨氏模量、单轴压缩拉伸试验等测试程序,得到尾砂的数值模拟力学性质;4)将实测结果与模拟结果进行对比,计算出相应的比值,选取正确的宏观力学参数输入尾砂材料。
输入尾矿砂粒子单元与水粒子单元的宏观力学性能参数,通过MatDEM软件自有转换公式得到微观力学参数。基于MatDEM软件进行自动训练材料操作,获得力学性质更加准确的材料。通过3次训练和自动调整,材料实测值与设定值之间的误差小于2%。然后将获得的材料力学性质参数输入给粒子单元。相关参数见表1~3。

表1 实测尾砂材料宏观力学参数
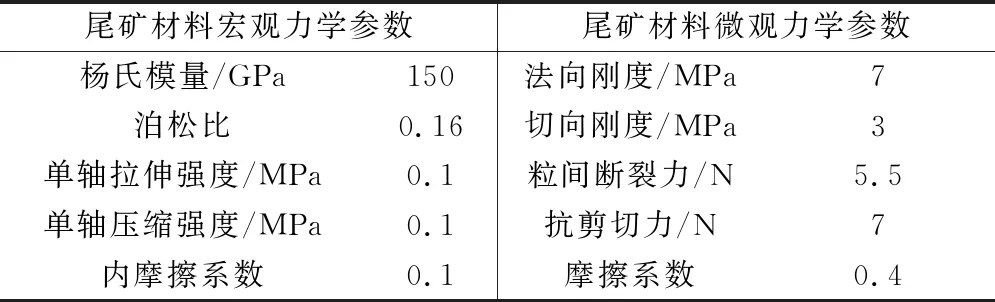
表2 输入的尾砂力学参数
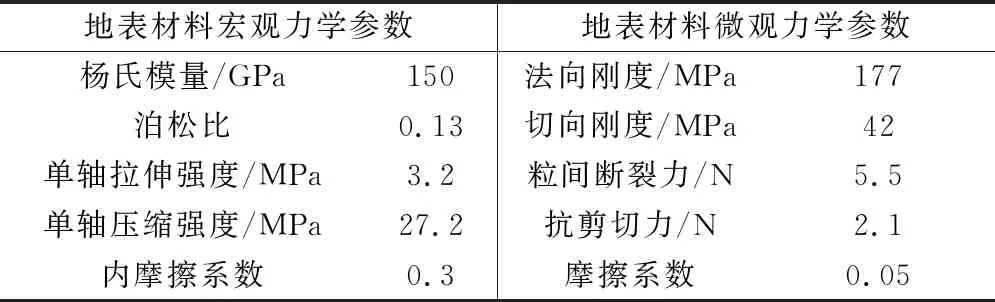
表3 地表材料力学参数
2 数值模型验证
2.1 瞬时全溃坝数值模拟
为了验证所使用的数值模拟软件的可行性,通过MatDEM软件进行模型堆积,然后对模型进行剪切,堆积出1个与文献[10]完全相同的矩形水箱模型。在此模型基础上进行瞬时全溃坝的数值模拟,并且对模拟结果进行分析。
模型分为上游与下游两部分,其中上游长5 m,水深10 m;下游长35 m,水深5 m。在水体处于静力平衡状态下,对溃坝模拟结果进行分析。溃坝水位模拟如图2所示,模拟中使用的水分子力学参数见表4。
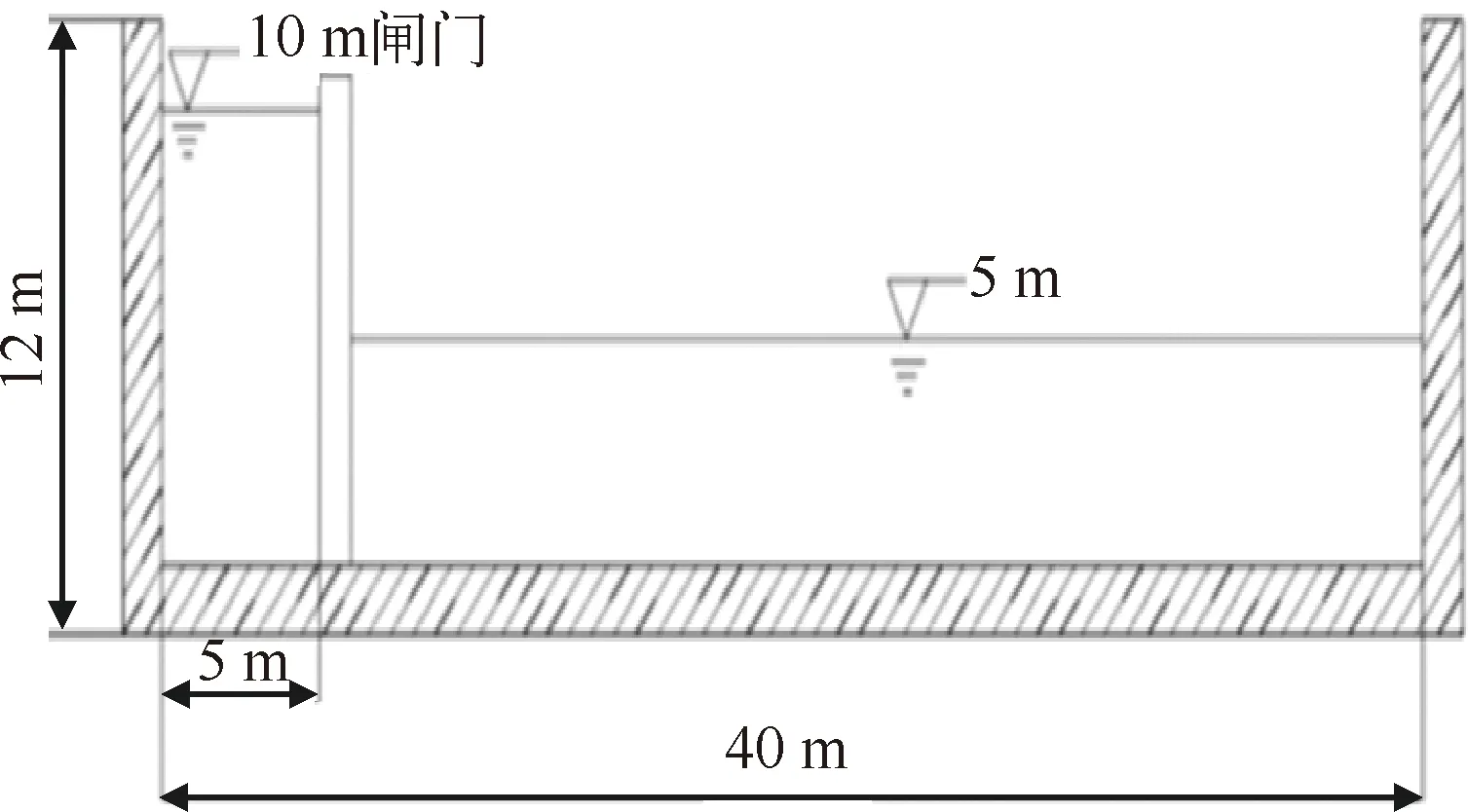
图2 溃坝水位模拟示意图
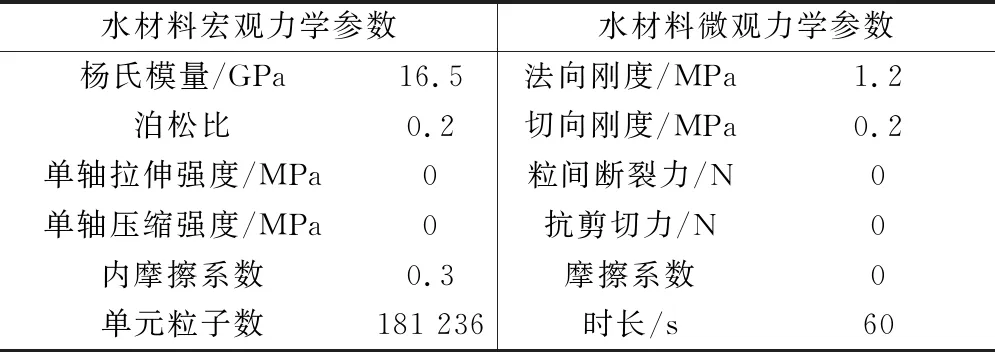
表4 水分子力学参数
用MatDEM软件的后处理功能对运算结果进行分析,得出的粒子位移如图3所示,自由液面曲线如图4所示。

注:左侧为文献[10]算例模拟结果,右侧为MatDEM软件模拟结果。
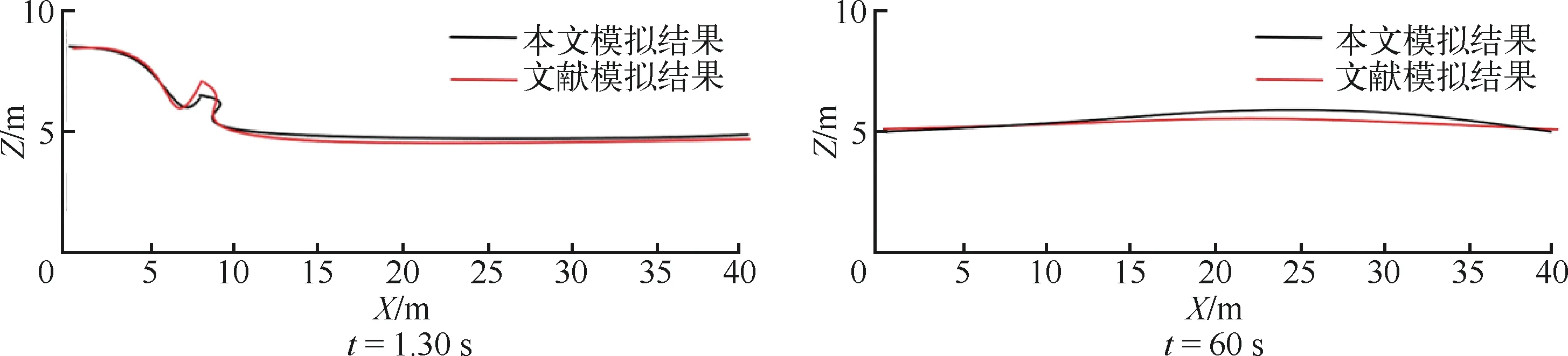
图4 自由液面曲线对比
由图3可知,MatDEM软件的模拟结果与文献[10]采用SPH方法(光滑粒子流体动力学方法)模拟的结果大致相似,证明了利用MatDEM软件进行液体动态分析的可行性。
由图4可知,由于接触单元、计算步长、单元体的个数不同,自由液面曲线与文献[10]存在一定差异。整个单元体的运动过程由下游水面上形成的1个涌浪开始,随着时间的延长浪涌逐渐消失,建立的模型合乎实际。
2.2 瞬时局部溃坝数值模拟
为了进一步验证计算模型的准确性,对前人开展的局部瞬时溃坝物理模型[11],进行基于离散元法的数值模拟。试验建立的局部溃坝数值模拟如图5所示。建1个长2.6 m、宽1.2 m的透明水箱;水箱分上、下游两部分,其上游水箱长0.8 m、宽1.2 m。在水箱前方设置2个宽0.025 m的固定单元挡板,形成1个0.3 m宽的溃口。单元个数为236 379。在水箱距溃口0.5 m的下游处设立1个长0.3 m、宽0.15 m、高0.1 m的矩形构筑物,用以模拟障碍物;在溃坝过程中实时检测水流的演进情况。所使用的水粒子力学参数与全溃坝模型相同。
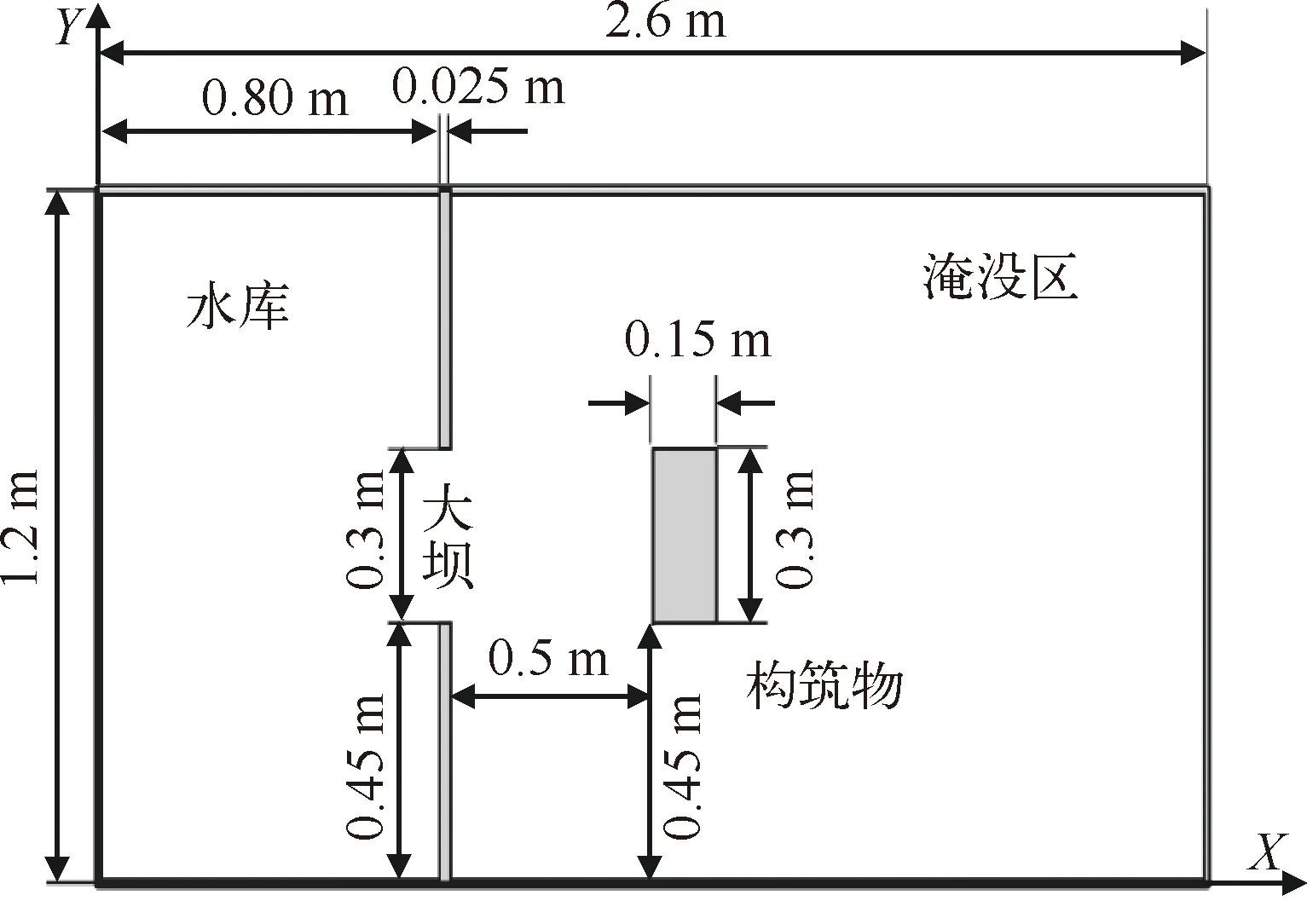
图5 局部溃坝的数值模拟俯视图
通过颗粒流离散元法对瞬时局部溃坝进行数值模拟,局部溃坝数值模拟对比如图6所示。选取了4个不同的时间,与文献[11]进行对比。在溃坝发生后的第0.38 s水流演进碰撞到了障碍物,之后水流将向障碍物两侧开始流动,且障碍物上游的水位随着时间的增加逐渐变深。在颗粒流离散元法下所模拟出的结果与文献[11]试验拍摄照片相似度较高,表明颗粒流离散元法可以较为准确地模拟瞬时局部溃坝水流演进情况。
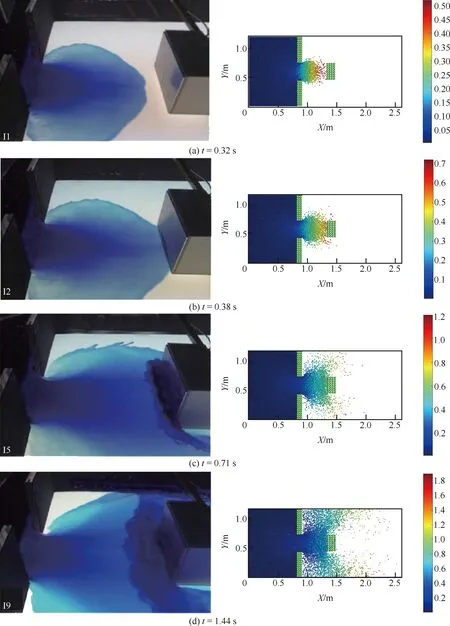
注:左侧为文献[11]试验现场照片,右侧为MatDEM软件模拟效果。
3 某尾矿库溃坝数值模拟结果
3.1 尾矿库基本情况
该尾矿库依托山形建设,尾矿库库区长180 m,平均宽100 m,库区内部为平原地貌。库区靠近下游一侧建立了长80 m初期坝,总库容约为532.5 万m3,比降约为0.002。该尾矿库采用上游式筑坝法,初期坝高30 m,初期坝坝顶高程2 450 m,内坡比为1∶2,外坡比为1∶4;尾矿堆积坝最终高程为2 550,坡比为1∶4。坝轴线长150 m,干滩坡度不小于3%。初期坝下游约150 m处有1处河道,河道宽约50 m;下游较为开阔。此尾矿库上游由山体包裹,所处的沟谷三面环山,该地区西部地势高,南部地势低,上下游间有较大的拐弯处。初期坝坝址高程最低点为495 m,该沟谷内植被情况良好,无较大突起,整体沟谷较为开阔。
以数值模拟方法对尾矿库瞬时溃坝之后尾矿堆积体的变化情况和下泄尾砂演进情况进行分析。尾矿库三维地形模型如图7所示。

图7 尾矿库三维地形模型图
3.2 尾矿库溃坝下泄尾砂淹没范围分析
模拟的尾矿库初期坝下游区域全长约1 200 m,在瞬时全溃坝发生后的第50 s时尾砂浆下泄演进至模型的边界,距离初期坝直线距离约800 m。
考虑到整体库区内的尾砂量较大,下泄时所带有的巨大能量可能会对模拟结果产生误差,因此本次溃坝总时长200 s,并经过多次模拟,选出误差较小的1次模拟。
尾矿库溃坝后,尾砂浆以较高速度向下游沟谷下泄演进。库区初期坝下游300 m区域为一段较为平直的山间谷道,溃坝后的尾砂浆在这段距离以较大的速度运移,如图8(a)所示。在运移300 m(大约15 s)时,尾砂浆将会与山体发生碰撞,从而向下游的右侧拐弯,转角大约30°,如图8(b)所示。因其第15 s时与山体发生碰撞,所以尾砂浆运移将不再均匀,有些尾砂因碰撞山体发生回弹,而有些尾砂因碰撞山体加大了运移速率,使得尾砂浆“头部”运移区不再紧密,呈散乱状态,如图8(c)所示。第1次碰撞山体后,尾砂浆继续向下游运移,因其下游区域高低不平且高程变化过大;所以尾砂在此区域运移时,颗粒运移速度有较大差异,运移的距离不同,总体呈现散乱不均匀状态。
尾砂浆运移至第50 s时,将会发生第2次的山体碰撞。由于此次碰撞是尾砂正面受到充分撞击,所以整体尾砂浆将会回弹,运移方向将会向西北方向偏转45°,如图8(d)所示。而此时因为受到山体碰撞的影响,尾砂浆所具有的动能被大大削弱,以较低的速率缓慢流入1片宽120 m的平缓区域。由于该平缓区域地势平坦,高程变化较小,可以减缓尾砂浆的冲击速率,同时对尾砂浆还有一定的贮存作用;从图8(e)可知,在100 s后大部分的尾砂浆将贮存在此。尾砂浆流出平缓区域后,将会运移通过高约50 m的陡坡,直至触碰到模型边界,如图8(f)所示。可以看出,从100 s到200 s的这段时间内,尾砂浆的运移变化不大,淹没范围至此确定。
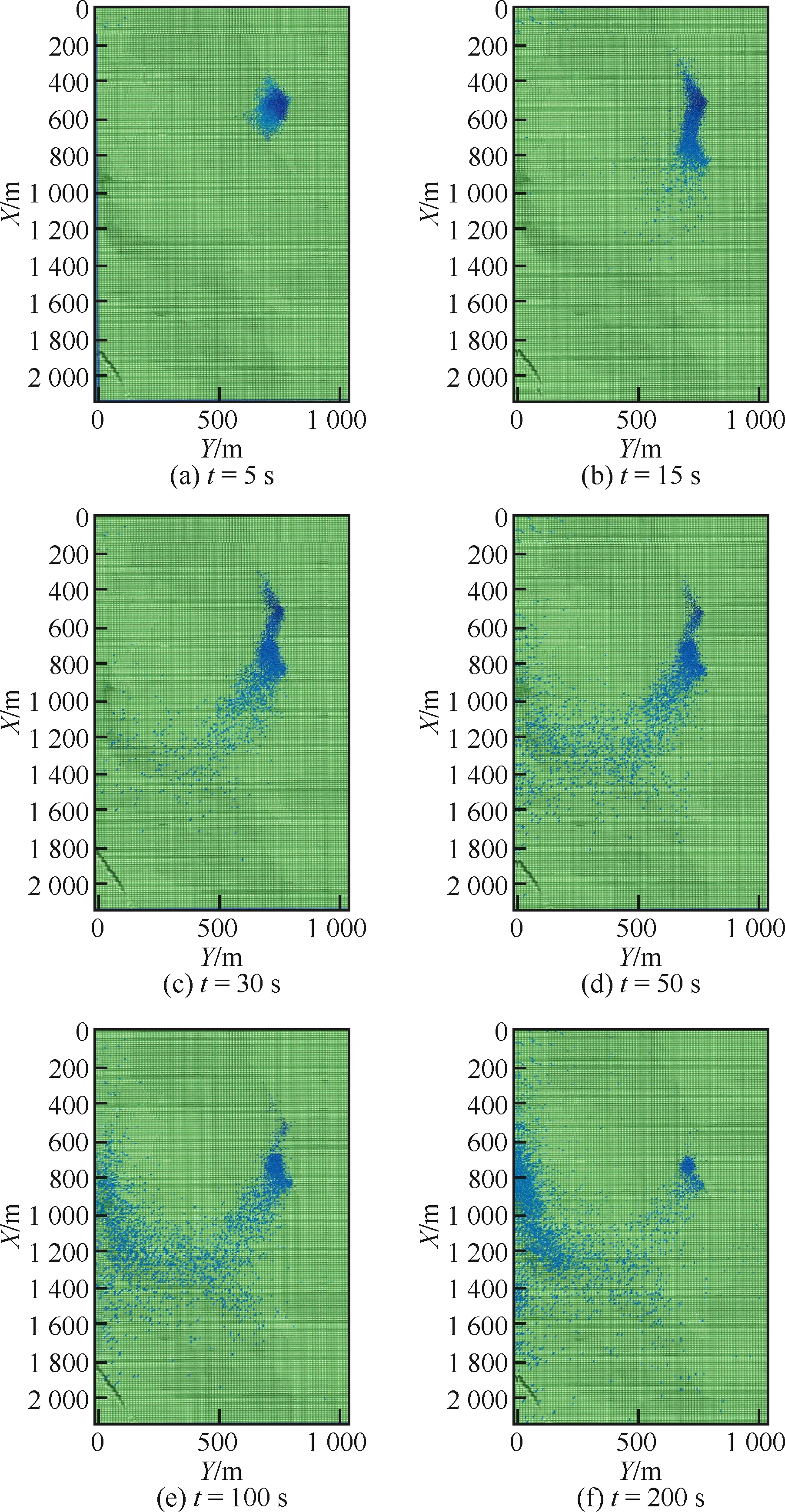
图8 尾砂浆淹没范围
3.3 尾矿库溃坝下泄尾砂速度规律分析
瞬时溃坝发生后尾砂浆锋面速度在5 s内达到30 m/s,如图9(a)所示。尾砂浆从初期坝下泄至第1次碰撞山体的过程中尾砂浆锋面速度保持30~40 m/s,变化较小,如图9(b)所示。当尾砂浆碰撞山体后,由于高程变化较大,尾砂浆锋面速度大幅增加,达到60~70 m/s,如图9(c)~(d)所示。当库区内的大部分尾砂浆下泄后,剩余尾砂浆速度减缓,约20~30 m/s,如图9(e)~(f)所示。尾砂浆最大速度出现在锋面,所以锋面含有最大的能量,所造成的破坏也是最大的。
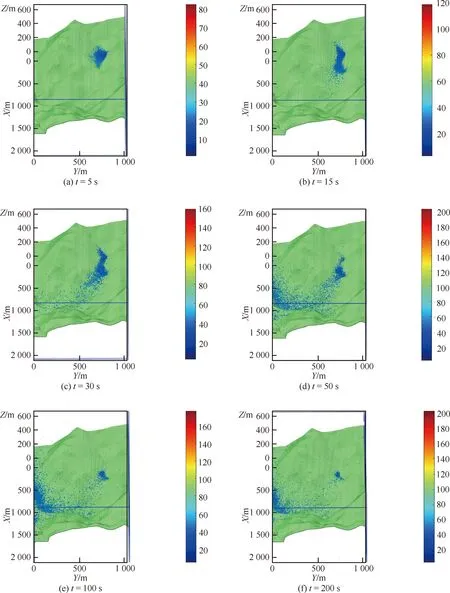
图9 尾砂浆速度分布
由模拟结果可知,所用的颗粒流离散元法将尾砂浆看成不连续介质,更好地模拟了尾砂浆在溃坝之后的运移过程,模拟结果贴近实际。与简化模型相比,利用颗粒流离散元法和MatDEM软件的三维建模结果,体现了实际地形对尾砂浆运移的影响,更具真实性。
4 结论
三维实际地形建模利用MatDEM软件,并在基于颗粒流离散元理论的基础上进行了改进,较好地体现了地形、高程变化对于尾砂浆运移的影响。将尾砂浆看成不连续、非均匀的流固混合浆体,使模拟得到的尾矿浆运移过程更符合实际。
