“双减”背景下低年级数学作业的改革与实践——以除法概念的建构为例

广东省深圳市福田区东海实验小学 李岚岚

2021年7月，“双减”政策正式出台。“双减”政策明确提出，全面压减作业总量和时长，减轻学生过重的作业负担。同时，对于低年级学生，除了在校适当安排巩固练习外，不布置家庭书面作业。

作业，是教师课堂教学反馈的重要组成部分，书面作业的缺席，给低年级学生的学习反馈造成很大的冲击。鉴于低年级的数学学习，主要以启动学生认知机制为主，鼓励学生发表自己的看法，用儿童化的生活语言去描述数学现象。因此，为增加学生的普适性交流和操作体验，笔者对学习内容进行整合，以适合低年级学生的学习方式，如实物操作、图形表征、抽象语言表达等，调整课后作业的切入方式，试图在不布置书面作业的同时，保证学生达到学业质量标准。下面将以除法概念的建构为例，谈谈“双减”背景下低年级数学常态作业的改革与实践。

一、知识内容整合

“分一分与除法”是学生第一次接触除法，理解除法意义、感悟乘除法之间的联系、学会用乘法口诀求商，是运算模块中的重要内容。教材中设置了三次分物活动，让学生在平均分的实物操作后，经历图表记录平均分的过程与结果，为学生认识除法打下基础，之后逐步数学化、符号化，引入除法运算。

二、系列作业设计

为保证学习内容的完整性，笔者依据课时重难点和数学思维培养点的不同，设计了系列作业。

（一）三次分物游戏

1.“分物游戏”

本节课是第一课时，借助小数目实物的平均分，让学生感受平均分的好处，积累平均分的活动经验。鉴于课堂中，学生未能经历平均分物的全过程，因此，作为分物起始课，让学生再次经历实物操作的平均分是很有必要的。

作业1

内容：准备15个圆片平均分（见图1），摆一摆、说一说，并画图记录过程(至少用2种分法)。

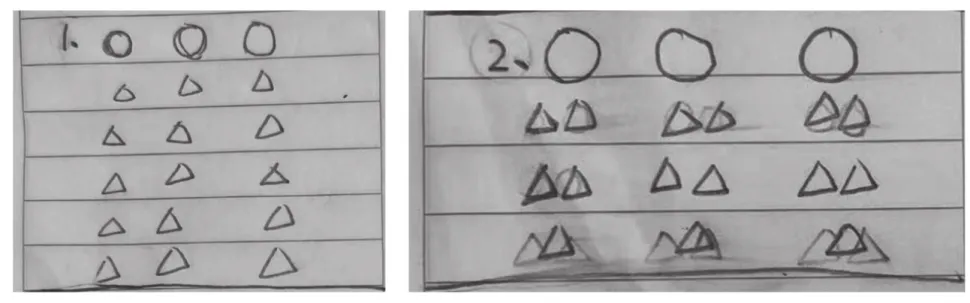
图1

目的：理解“平均分”的含义，感受平均分的过程。

形式：实物操作，画图表征，拍照提交。

范例：15个圆片，平均分成3份，每份有5个。

本次作业强调实物操作与画图表征，让学生充分感受平均分的本质：虽然分法不同，但是每次分的数量相同，而且结果也是每份一样多。

2.“分苹果”

本节课旨在让学生深入感受平均分的2个现实模型，因此，该内容学习不再是经历简单的实物操作，而需借助分析，找到2个模型已知条件与所求问题间的差别，再从结果“每份同样多”，强化学生对平均分的理解。

作业2

内容：根据板书（见图2），说一说两次分苹果的相同与不同。

图2

目的：深入感受平均分的2个现实模型。

形式：画图讲解，提交视频。

本次作业，学生对“总数÷份数=每份数量”“总数÷每份数量=份数”这两个除法模型有了直觉上的感知，讲解过程通过“画一画”“圈一圈”的形式对第1课时用画图法表示分的过程，也有了进一步强化。

3.“分糖果”

本节课借助大数目平均分，让学生感受平均分策略的多样性。有了第1课时的基础，学生对大数目平均分的方法并不陌生，因此，本节课以预学作业形式切入，新授课前，可以让学生提前独立完成。

作业3

内容：课本第63页第1题（见图3）

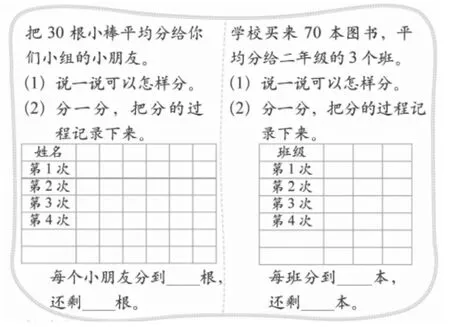
图3

目的：掌握大数目物品平均分的方法，体会平均分方法的多样性与合理性。

准备：若干豆子（不少于100粒）。

要求：

（1）把30粒豆子平均分给6个人，把70粒豆子平均分给3个班；

（2）说一说可以怎样分；

（3）把分的过程记录下来。

形式：实物操作，表格记录，拍照提交（分的照片+记录表）

通过本次预学作业的反馈，大部分学生能举一反三，借鉴小数目平均分的方法完成任务。（见图4）

图4

但是，个别学生的作业存在以下问题：

（1）图文不对应，分的过程和填的表格不一致，将份数与每份数量的意义搞反了（见图5）；

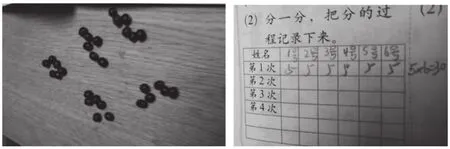
图5

（2）有剩余的平均分，剩下的个数需小于份数，不能继续再分，部分分了一半就不再继续分了（见图6）。

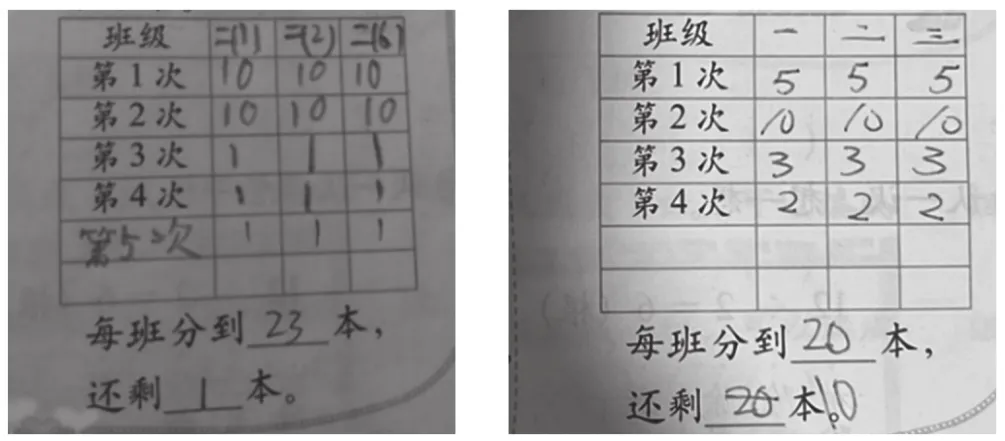
图6

教师借助反馈，课堂讲评时，通过有层次地呈现学生的预学单，通过对图表的一一剖析，再到出错点的生生思辨，大数平均分方法的提炼在讨论交流中很快得以突破。

（二）除法概念的建构

1.“分香蕉”

本节课通过分香蕉的情境和经验，抽象出除法算式，要求学生会用除法算式解释平均分的具体过程，理解除法的意义。

作业4

内容：课本65页第1题（见图7-1、图7-2）

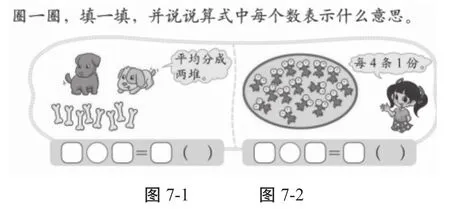
目的：用除法算式表示并解释平均分的过程。

要求：描述题意（已知条件+问题）+列式解决+算式中每个数表示的意思。

形式：语言表达。

范例：

图7-1：有8根骨头，平均分成2堆，每堆有几根骨头？用除法算式8÷2=4（根）计算，“8”表示8根骨头，“2”表示平均分成2堆，“4”表示每堆分到4根骨头，总数÷份数=每份数量。

图7-2：有16条金鱼，每4条分1份，可以分成几份？用除法算式 16÷4=4（份）计算，“16”表示 16 条金鱼，“4”表示每4条分1份，“4”表示平均分成了4份，总数÷每份数量=份数。

学生在不同的图中，进一步学会用抽象的除法算式去解释平均分的2个现实模型。

2.“小熊开店”

本节课旨在结合购物问题，让学生们理解乘法、除法、减法之间的联系，并掌握用乘法口诀求商的方法。这节课容量相对较大，因此，笔者在上一课时练习五的巩固练习后，借助表达作业提前渗透了乘除互逆关系。

作业5

内容：课本67页第5题（见图8）

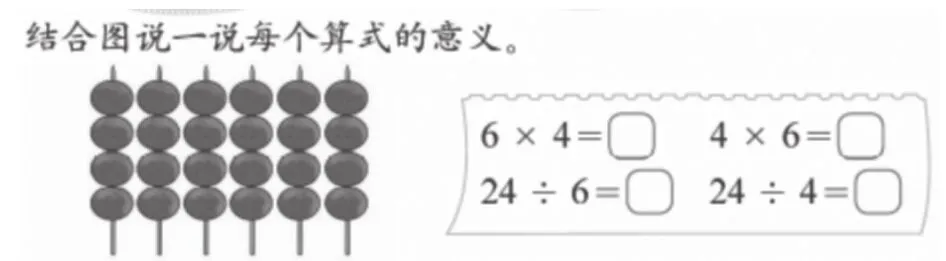
图8

目的：同样一幅图，可以用乘、除两种算式表示，体会乘除的互逆关系。

要求：根据图意说清每个算式的意义。

形式：语言表达。

范例：

有6串糖葫芦，每串有4颗，一共有多少颗糖葫芦？可以用乘法 6×4=24计算，份数×每份数量=总数。

1串糖葫芦有4颗，有6串，一共有多少颗糖葫芦？可以用乘法 4×6=24计算，每份数量×份数=总数。

一共有24颗糖葫芦，平均分成6串，每串有几颗？可以用除法24÷6=4计算，总数÷份数=每份数量。

一共有24颗糖葫芦，4颗为一串，平均分成几串？可以用除法24÷4=6计算，总数÷每份数量=份数。

基于上述表达的提前渗透，学生对乘、除之间的联系有了模模糊糊的认知，新授课时，以加、减法之间的联系作为切入点（见图9），学生顺理成章地发现能用乘法口诀求商，再通过多种方法的比较，体会乘法口诀求商的简便性，突破难点。

图9

新授课后，教师还可以引导学生通过语言表达练习进行强化巩固。

作业6

内容：课本69页第1题（见图10）

图10

要求：说清楚如何用乘法口诀求商。

形式：语言表达。

每日一题的表达作业，素材来源于教材，内容聚焦数学思辨点，层层递进，让除法概念的建构真正得到了巩固与落实。当然，数学抽象概念的建构是为了解决生活问题，适当的时候，还可以设计发散性的拓展练习。

作业7

内容：结合日常生活，提出一个用除法解决的问题。

目的：回顾除法的生活情境（分物品、购物、排队等），灵活运用除法解决问题。

形式：语言表达。

三、作业设计思考

从上述的单元系列作业设计可以看出，不同的教学内容，作业功能、完成方式、作业反馈都是不同的。

（一）作业功能

从作业辅助教学的功能上看，可分为预学、导学和延学作业。学生有一定基础，属于知识迁移的内容，可以设计预学作业，如作业3和5。对于初步概念建构后的强化练习，低年级学生需要规范的引导示范，课堂指导后，设计导学作业，能进一步规范练习，如作业1、2、4和6。而在知识建构完成后，还可以设计课本之外对应的拓展延学，如作业7。

（二）作业方式

显然，对低年级学生来说，数学思维的可视化表达，没法处处落笔梳理，所以，教师给学生搭建够得着的脚手架，让学生把数学思维“说”“做”“画”“写”出来，进而窥探学生真正的想法，帮助学生学会用数学的眼光观察世界，用数学的思维分析世界，用数学的语言表达世界。

（三）作业反馈

一课一表达作业的推进，旨在通过聆听和收集学生的数学思考，将一个个零散点进行强化与沟通，帮助他们建立数学网络式结构。因此，围绕完成情况，进行整体点评分析、模范作业借鉴学习以及错例拨乱反正，是很好的反馈方式。生生思辨，常常会碰撞出预设之外的火花，每一次发现问题的自我补充，都是学生对知识的自我建构，也是教师对教学的重新认识。

以生之“思”，促生生之“辩”，作业的价值才能最大化！“双减”政策，让一线教师，聚焦教学思辨点，为学生的学习提供更有价值的资源以及更精准的指引，将作业从数量意义上的“减法”、转为内涵价值上的“加法”，最终实现学生学习效能的“乘法”。