基于Kolmogorov前向方程评估甲型H1N1流感疫情的动态变化*

闫琴玲，唐三一

（1.长安大学 理学院，西安 710064；2.陕西师范大学 数学与统计学院，西安 710119）

引 言

数学模型在突发性传染病疫情防控中发挥着至关重要的作用.它们可以用来刻画传染病传播规律、评估控制措施的有效性以及预测潜在传染性等.而针对突发性传染病，大多数研究者主要是建立基于种群水平的确定性模型.然而，越来越多的研究表明，由于人口事件的随机性，人口随机效应可能导致确定性模型的结果与实际情形显著偏离[1-5].因此，一般情形下，人们基于事件驱动的模型模仿真实系统的现实行为[6-7]，即将一系列复杂的生物现实行为嵌入基础模型，并为人们提供直观的建模框架.然而，对于单次模拟，不能确定模拟的动力学是代表平均行为还是仅仅是由于偶然事件产生的异常值.因此，为得到对应变量(或参数)的置信区间，研究者们需要进行大量的重复模拟.

许多现存的近似方法(如扩散近似和矩闭合技术)通过给出近似解析解以避免大量模拟种群行为及其变化[5,8].然而，只有当种群规模足够大时，这些方法才是比较准确的.而通常研究的问题是种群规模较小的随机模型，且随机性对动力学行为具有相对较大的影响，需要探索适用于种群规模较小的方法.因此，我们应用一种Markov 过程——Kolmogorov 前向方程(KFE)，来研究种群规模较小时的随机模型.

KFE 是一个关于处于每种状态概率的动态微分方程系统，其动态变化大小由状态之间的转换速率决定[9-10].因此，通过求解微分方程系统，可以得到随机系统所有可能行为的完整描述.并且随着计算机计算能力的不断提高，这些技术越来越适用于实际问题.用KFE 方法生成大量微分方程的解，在现代计算机上运行相对简单且快速[5,11-14].此外，就处于每种状态的概率而言，它是线性的.它通常把与种群动力学相关的复杂非线性简单地包含到矩阵项中.通过此方法，可以用更简单的矩阵和向量运算来构建方程，这大幅度地加快了计算速度.

另一方面，已有文献研究表明，在突发性传染病爆发过程中，人们的行为可能发生改变(如戴口罩、勤洗手、避免到公共场所等).而由于个体行为改变，感染风险会降低[15-16].

为此，本文基于2009年西安市第八医院甲型H1N1 流感数据(包括新增病例数及累计病例数)，如图1所示，建立个体决策心理模型；把行为改变率嵌入基于个体水平的SIR 模型，并基于此推导得到KFE，探究此传染病在整个传播过程中每种状态的概率分布，从而高效地进行甲型H1N1 疫情的防控.

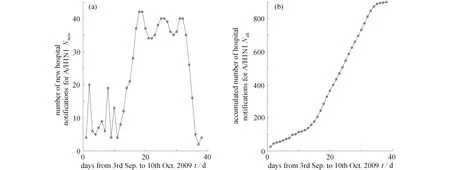
图1 2009年9月3日至10月10日西安市第八医院甲型H1N1 病例数：(a)新增病例数； (b)累计病例数Fig.1 The hospital notifications for A/H1N1 from 3rd September to 10th October 2009 in Xi’an 8th Hospital: (a)the number of new hospital notifications;(b)the accumulated number of hospital notifications

1 基于甲型H1N1 数据的个体决策心理模型

基于文献[17]的观点，健康信念模型(health belief model, HBM)结构可用于揭示突发性传染病爆发期间的行为决策与情景信息之间的关系.因此，本节主要借助于HBM 结构与情景信息之间的关系(包括自觉严重性、自觉易感性、自觉障碍、自觉效益)，建立具有以上四种HBM 结构和行为改变率的logistic 模型(记为LHBM)，采用非线性最小二乘法对模型中的参数进行估计.LHBM 结构的详细描述在附录以及图A1 给出.

为了估计方程(A6)中的未知参数 (O0，O1，O2，O3，O4，δ，λ，ξ，τ，η )，基于四种社交网络、LHBM 流程图(图A1)以及文献[18]，我们模拟从9月3日到10月10日，2 004 个个体(每个个体每天基于LHBM 结构独立作出决定)的行为改变率，并对行为改变率数据进行拟合.2 004 个个体(假设易感人数2 000，感染人数4，恢复人数0)中每个个体的行为改变率的估计值pe(i,t)，所有个体行为改变率的平均值(t)和其95% 置信区间如图A2所示，其中黑色区域、白色曲线分别代表2004 个个体的95%的置信区间及均值((t))，圆圈表示p(t)的真实值.估计得到的参数的平均值及标准差如表 A1 所示.由于规则网络残差绝对值的和最小，因此，由规则网络得到的平均行为改变率p¯(t)将会用于以下模型的研究.

2 基于甲型H1N1 数据的KFE

2.1 KFE 的建立

基于文献[18]中的模型选择结果，这里，我们考虑行为改变率(t)，并将平均的行为改变率p¯(t)以指数函数的形式嵌入经典的SIR 模型，得到如下系统：

其中S(t)，I(t)，R(t)分别表示易感人数、感染人数和恢复人数.

根据KFE 的有关知识[9]，模型(1)的反应式可表示为

记X(t)=[S(t),I(t),R(t)]T(T 为转置，t≥0)为系统(1)中各仓室的人数，已知初值X(0)=x(0)，则易知{X(t),t≥0}是 一个多元随机过程.设Z(t)=[Z1(t),Z2(t)]T为模型(2)中两种反应在 [0,t)内发生的次数，则{Z(t),t≥0}是一个计数过程，称为状态更新度(DA 过程)[19].依据DA 过程与群体过程之间的关系，有如下方程[9]：

其中

对于给定的x(0)，X(t)由Z(t)唯一确定.

基于系统(2)，对于任意的m(这里m∈{1,2})，在 [t,t+dt] 内，反应m发生的概率是 πm(x)dt+o(dt)[20].其中，π1(x)=βe−αp¯(t)S(t)I(t)/N和 π2(x)=γI(t)是 系统(2)在时刻t的倾向函数.因此，由于 {Zm(t),t≥0} 是Markov 过程，强度为 πm(X(t))，经过推导可以得到以下KFE：

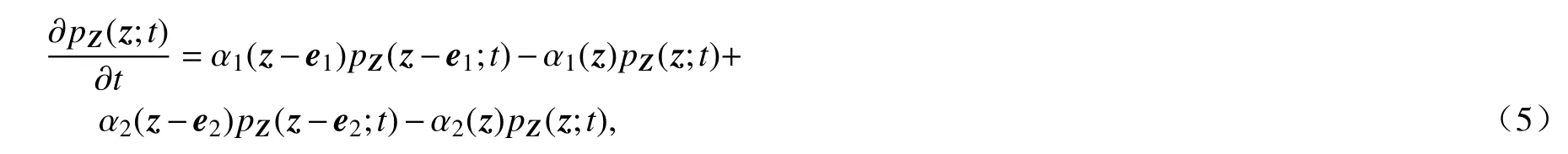
其中pZ(z;0)=δ(z)，δ (z)是 一个Kronecker δ 函数；e1=[1,0]T,e2=[0,1]T；对于m∈{1,2}，有

依据方程(3)中Z(t)和X(t)的关系，可得pX(x;t)的概率函数满足

其中 B (X)={z|x=x(0)+Sz}.因此，通过求解方程(5)可以得到方程(3)的动态变化特性.

此外，对于 T =[0,tmax]，有限样本空间 Z (元素zk=[z1k(t),z2k(t)]T,k=1,2,···,K)，基于概率的性质，则pZ(z;t)满足

令K×1 向量 φ(t)的 元素 φk(t)=pZ(zk;t)(k=1,2,···,K).则基于方程(5)，有如下K维微分方程：

对 于给定的时刻t，A(t)是K×K矩阵；初始值φ (0)=[1,0,···,0]TK×1.

2.2 KFE 的数值求解

对于给定的t(t=1,2,···,38)，易知矩阵A(t)具有三角性、稀疏性、稳定性[9].因此，对于以下方程

采用隐式Euler(IE)法计算 φ(t)在 离散时间点tj=jτ(j=1,2,···;τ=0．01)的估计值(tj).这里I是单位矩阵.因此，对于给定的(0)=φ(0)和tj(j=1,2,···)，通过方程(10)可以得到概率质量函数pZ(z;t).

基于文献[18]，设 α =0．011 57, β =0．755 5, γ=0．545 2为参数的初始值.又因在疫情初期有4 个感染个体，因此设S(0)=2 000,I(0)=4,R(0)=0 为易感人数、感染人数和恢复人数的初始值.(t)是第1 节中N=2 004个个体行为改变率的平均值.K=(S0+1)×(S0+I0+1)=2 001×2 005=4 012 005是样本空间的大小.因此，在给定精度下，利用IE 法计算KFE(10)的精确解，从而得到模型(5)的精确解.同时，对于模型(1)，采用Gillespie 算法进行参数估计和模型拟合(基于1 000 次Markov-chain Monte-Carlo (MCMC)模拟)，从而对结果进行进一步的比较[6,20].

考虑到R(t)=N−S(t)−I(t)及无病状态发生的概率很高，我们只需要计算感染人数与易感人数的联合条件概率质量函数P(S(t),I(t)|I(t)>0).图2(a)和(b)分别刻画了在第38 天的概率质量函数P(S(t),I(t)|I(t)>0)及其等高线图.由图2可知，假设最初有4 个感染个体，到第38 天，感染人数与易感人数的联合条件概率达到最大(1 ×10−4)，此时新增病例数约为 5 ～15，易感人数约为 750 ～850，这与实际情况基本一致(图1(a)).其次，图2(c)给出了第38 天恢复人数的条件概率质量函数P(R(t)|I(t)>0).由图可知，到第38 天时，恢复的概率达到最大(3 ．5×10−3)，约有1 200 个个体恢复.

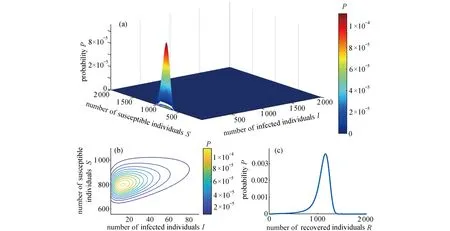
图2 流感流行38 天计算出的概率质量函数的快照： (a)到第38 天时，感染人数与易感人数的联合条件概率质量函数P (S(t),I(t)|I(t)>0)；(b)概率质量函数的轮廓图；(c)第38 天恢复人数的条件概率质量函数P(R(t)|I(t)>0)Fig.2 A snapshot of the calculated probability mass function at the end of the 38 d influenza epidemic: (a)joint conditional probability mass function P(S(t),I(t)|I(t)>0)of infected and susceptible individuals; (b)the contour of the calculated probability mass function; (c)conditional probability mass function P (R(t)|I(t)>0)of recovered individuals

再次，易感人数、感染人数和恢复人数均值(均值 ±标准差)的动态变化可以根据P(S(t),I(t)|I(t)>0)和P(R(t)|I(t)>0)直接计算得到，如图3(a)、(b)和(c)所示.通过比较图3(b)与图3(d)，得到IE 法的结果比Gillespie算法的结果更好.此外，Gillespie 算法需要进行大量随机模拟才能准确估计P(S(t),I(t),R(t)).因此，与Gillespie 算法相比，IE 法更优.

3 最终规模

根据Kermack 等的定义，最终规模R∞是指，对于突发性传染病，引入少量感染个体后，被感染人数在易感人群中(并最终恢复)的比例[21].因此，根据文献[21]，关于最终规模有以下关系式：

其中R0是基本再生数.

3.1 R0的计算

对于方程(1)，根据文献[22-23]中R0的定义(指引入一个感染个体，在感染周期内，平均出现的新感染个体的数量)，设新发感染和转移项分别用一维向量F，V表示，则

从而得到下一代一维矩阵

根据Wang 等对谱半径的定义，R0可由感染算子的谱半径L计算得到[23]，可表示为

对于周期的传染病系统(1)，根据Becar 等的计算方法可得[22]

其中参数λ ∈(0,+∞).设系统(1)在 Rm上的演化算子为W(t,s,λ)，则R0为 ρ (W(ω,0,λ))=1的正根，其值为

这里最大的观测数据时间点T1=38.

对于系统(1)，根据文献[18]得到的参数 α , β , γ 的值，得R0的估计值为1.314 3(95% 置信区间1.3127～1.3160).

3.2 R∗∞的计算

令x=R∞(x∈[0,1))，则方程(11)可表示为

记f(x)=1−e−R0x−x，则易知x∗=和x∗=0是f(x)=0的两个根.

f(x)对x求导，得

因此，对于方程(17)的根，根据参数R0的阈值水平，考虑以下三种情形：

(ⅰ)当R0<1时，f′(x)<0，即f(x)在 (0,1)上 单调递减.又因为f(0)=0，因此，当R0<1时，x∗=0是方程(17)的唯一解.

(ⅱ)当R0=1时，f′(x)=e−x−1<0 .因此，当R0=1时，x∗=0是方程(17)的唯一解.

(ⅲ)当R0>1时，设f′()=0，则=ln(R0)/R0>0.易验证<1显然成立.

又因为

(a)当x<时，f′(x)>0； 当x>时，f′(x)<0； 因此，f(x)在 区间(0,)上单调递增，在区间(,1)上单调递减.

(b)f(1)=−e−R0<0，f′()=1−(1+lnR0)/R0<1且f′>0.因此，存在唯一的解x∗∈(1)使 得f(x∗)=0,x∗的显式表达式如下：

综上，方程(17)有两个解，分别为0 和

其中

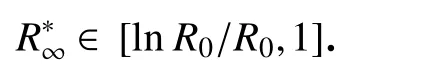
4 讨论与结论

本文建立了一个基于个体水平的随机SIR 模型，通过Markov 过程，推导出KFE.然而，只有对含有限个体的群体，才能得到KFE 的解析表达式[10,24].对于含有大量个体的群体，只能采用近似法或数值解方法得到其解.对于随机的SIR 模型，基于DA 过程，Jenkinson 等[9]采用IE 法得到KFE 的精确解，并且证实了此方法优于Krylov 子空间逼近法及Gillespie 算法.因此，本文通过IE 法得到了KFE 的数值解、传染病传播过程中感染人群与易感人群的联合条件概率质量函数、最严重的时间段和相应的概率.此外，对于随机SIR 模型的求解，IE 法比Gillespie 算法更好.

我们的研究有以下局限性.首先，考虑到计算成本和网络的复杂性，在第1 节我们仅选择对2 004 个个体进行随机模拟.另外，由于A(t)是K×K矩阵(K=(S0+1)×(S0+I0+1))，随着S0和I0增 大，A(t)计算量大幅度增加，考虑计算成本，在第2.2 小节数值计算仍然选择总人数为2 004.

综上，本研究通过基于个体水平的随机SIR 模型，推导并数值求解KFE，得到了疫情爆发过程中最严重的时间段以及对应的概率分布，从而能更快、更准确地了解甲型H1N1 流感的传播过程，因此有助于高效地进行甲型H1N1 的疫情防控.

附录 LHBM 的建立

LHBM 模型的详细描述如下[18].

自觉易感性自觉易感性(perceived susceptibility)是指人们对感染传染病最大可能性的信念[26]，记作P1，定义如下[27]：

式中

其中参数λ 是低敏感性到高敏感性的阈值水平，st，ct−1，δ分别表示累计病例数、新增病例数以及折现率常数.

自觉严重性自觉严重性(perceived severity)是指人们对一种传染病严重程度与其后遗症所持的观点[26].这里假设自觉严重性是媒体报道量的函数(记作M(t))，记作P2，即

其中参数 τ 表示个体自觉严重性从高到低的阈值水平.

自觉障碍自觉障碍(perceived barriers)用于描述人们采取一些行动的成本，包括有形成本和心理成本[26]，记作P3.我们使用四种经典网络刻画个体之间的连接关系，包括小世界(WS)网络[28]、规则网络、随机网络[29-30]、Newman 和Watts(NW)网络[31].从而有(详见文献[18])

其中，集合 Ωi={j|j≠i} 表示所有与个体i有连接的个体，ni为集合 Ωi的大小；当个体j戴口罩时，Aij等于 1，否则等于 0；参数 η 是低障碍到高障碍的阈值；Dij表示i和j之间的亲密关系，即Dij=md/dij，其中，md是i和j之间的最小距离；社交网络中总人数为N1，有N2个戴口罩的人,与i连接的邻近节点数记为c.

自觉效益自觉效益(perceived benefits)是人们为降低由传染病引起的风险而对采取某些行动有效性的信念[26]，这里设自觉效益接触人数的函数[29]，记作P4，定义如下(详见文献[18])：

其中，参数ξ 是低效益到高效益的阈值水平.

因此, 具有以上四种HBM 结构和行为改变率的logistic 模型(记为LHBM)，定义如下[27]：

这里,k=1,2,3,4 分 别代表自觉易感性、自觉严重性、自觉障碍和自觉效益；p(i,t)是第i个体第t天的行为改变率；Ok表示两种结构的比率；xk(i,t)的取值为 1 表示LHBM 结构为高状态，为 0 表示低状态;O0是校准常数.

基于四种网络，2 004 个个体从9月3日至10月10日估计的行为改变率(pe(i,t))和实际的行为改变率(p(t))之间残差绝对值的和分别为2.314 2E+3，2.785 7E+3，2.510 8E+3，2.403 1E+3.

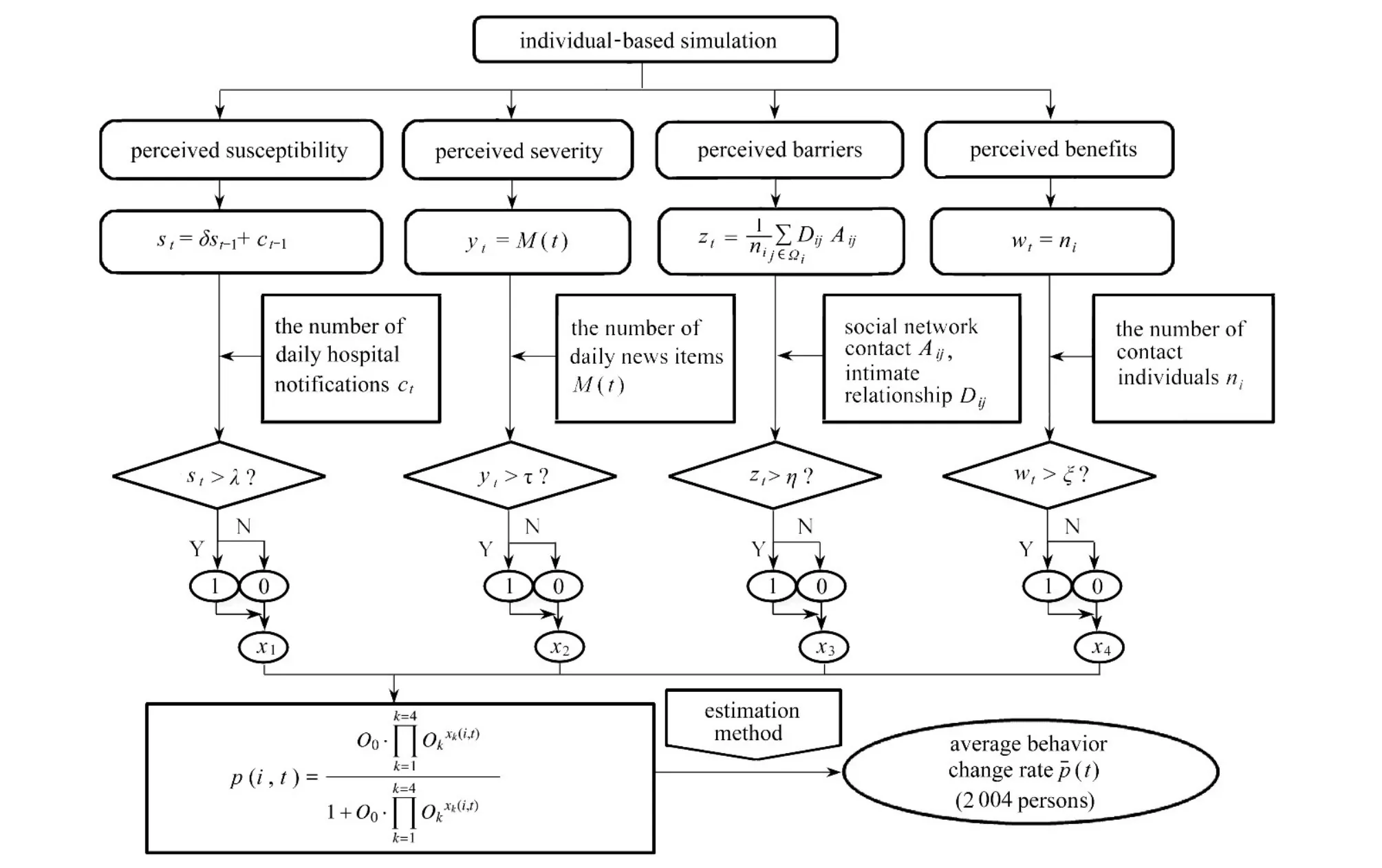
图A1 基于个体的LHBM 流程图Fig.A1 The individual-based scheme of the LHBM

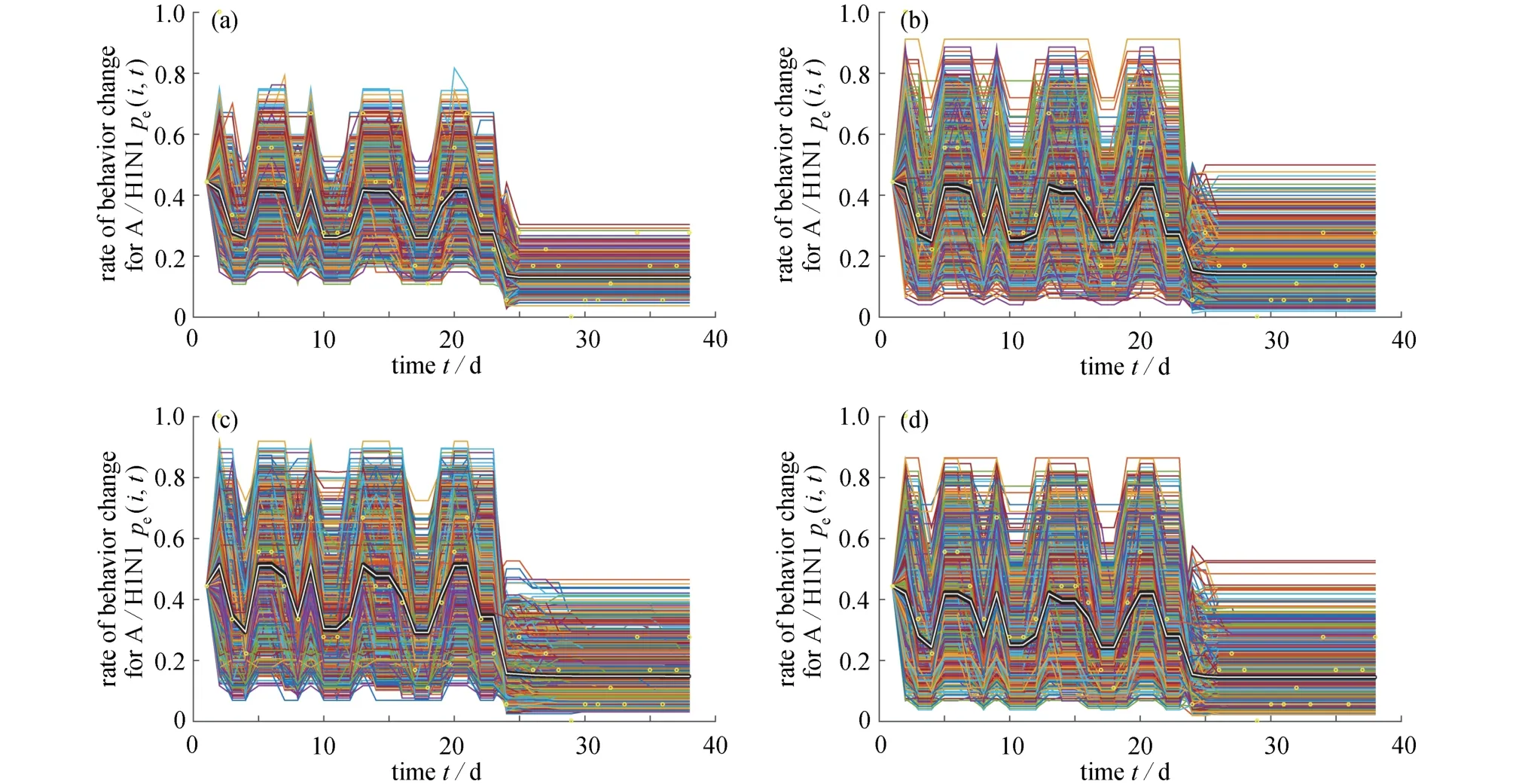
图A2 基于模型(A6)，对2 004 个个体的个体行为改变率 pe(i,t)进行估计： (a)规则网络; (b)小世界(WS)网络; (c)NW 网络; (d)随机网络Fig.A2 The estimation of individual behaviour change rate pe(i,t)for 2 004 persons based on model (A6): (a)the regular network; (b)the small-world (WS)network; (c)the Newman and Watts (NW)network; (d)the random network

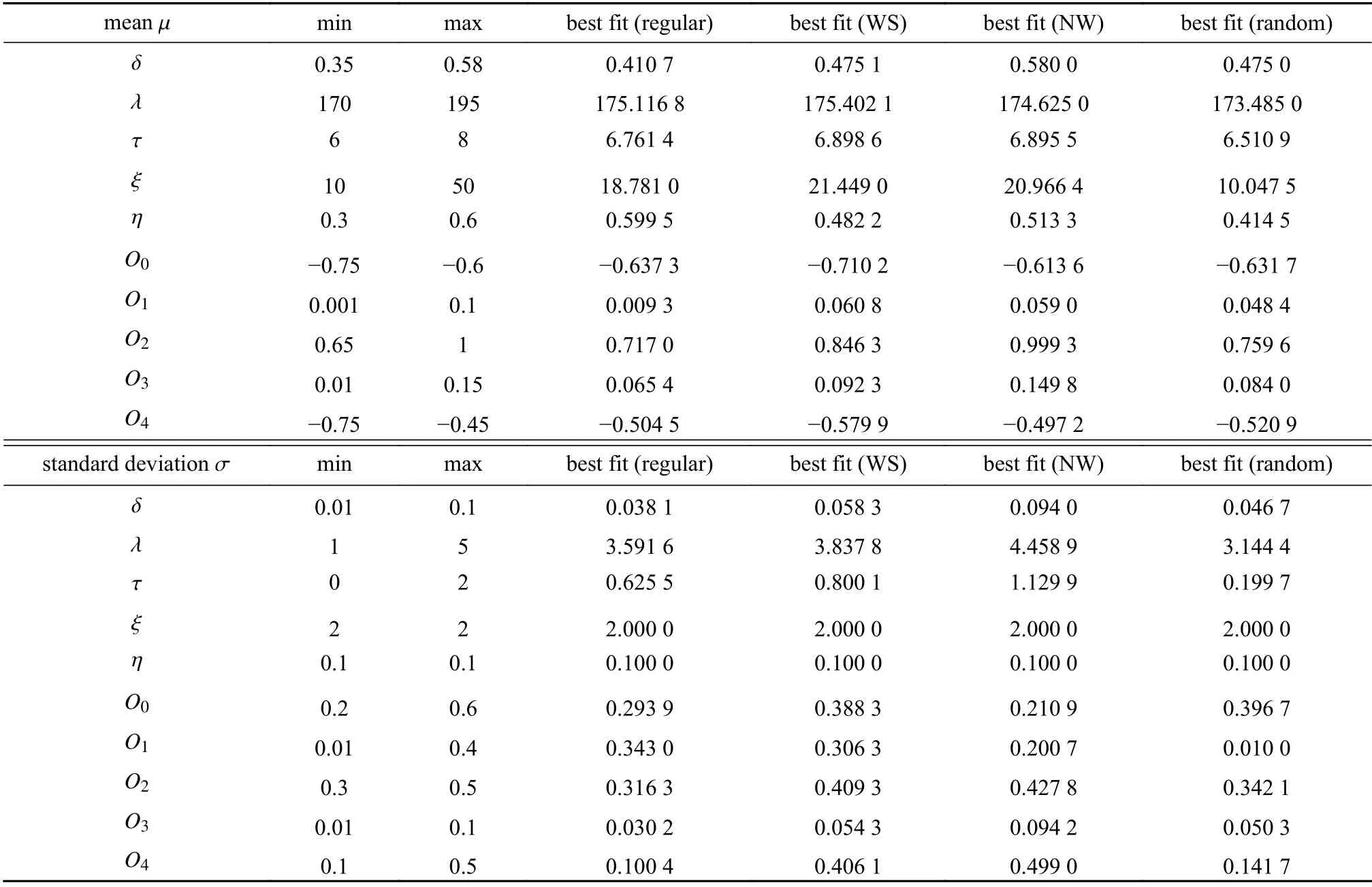
表A1 在四种经典的社交网络结构下, 模型(A6)所有参数均值和标准差的估计值及取值范围Table A1 The estimated values and ranges of means and standard deviations for all parameters of model (A6)with 4 classical social networks