不对称裂缝单井渗流模型的Green函数构造方法*

姬安召，王玉风，张光生

（陇东学院 能源工程学院，甘肃 庆阳 745100）

符号说明

引 言

在研究压裂油气储层性质方面，诸多学者提出了许多压裂井试井分析方法[1-3].Gringarten 等[4]对裂缝井瞬态压力分析和类型曲线分析的发展做出了一定的贡献.考虑裂缝导流能力，文献[5-6]提出了垂直裂缝井的半解析解和解析解.但这些研究成果都是基于对称均匀流量裂缝而言的.然而，在实际生产现场中，很难保证压裂裂缝关于井筒对称.在不对称裂缝渗流研究方面，Crawford 和Landrum[7]首先研究了裂缝不对称性问题，但没有得出有意义的结论.直到1979年，Narasimhan 和Palen[8]讨论了在恒定流量下裂缝不对称性对渗流特征的影响.后来，Bennett 等[9]简要分析了裂缝不对称性对产量的影响.Resurreicao 和Fernando[10]在恒压条件下获得了实空间中的解析解，研究得出在流体流动过程中，当裂缝不对称系数为0.8 时，流动速度倒数会受到不对称系数的严重影响，当不对称系数为1 时（即裂缝只有一翼的情况），影响会更大.Berumen 等[11]采用数值模拟方法，提出了不对称裂缝井的恒速解.Tiab 等[12]将TDS 技术（利用井底压力及压力导数的双对数曲线的重要特征点、特征线进行分析和计算储层的相关参数技术）应用到不对称裂缝的双线性流模型和线性流模型，以计算裂缝的导流能力和不对称因子，同时采用回归分析方法建立了既考虑裂缝导流能力又考虑裂缝的不对称因子的线性压力方程.文献[9-10]提出了单一不对称裂缝渗流模型的积分变换解法.文献[12]提出了采用Green 函数方法求解不对称裂缝的渗流数学模型，但未给出Green 函数的构造方法.田建涛等[13]针对水力压裂监测方法提出了不对称裂缝解释方法.这种监测和解释不对称裂缝的技术可以与理论解释模型进行对比分析，能更加合理准确地解释水力压裂裂缝的几何形态及相关参数.文献[14]对水平井多段压力裂缝采用有限元方法进行了求解分析.文献[15]对于压裂的多翼裂缝，采用映射变换方法，把裂缝两翼映射到x轴上，再通过无因次变换，在椭圆坐标系中对多翼裂缝的拟稳态渗流进行求解，然后通过数值计算方法对求解的结果进行了分析.文献[13-15]的这些研究成果都是通过数值模拟方法研究了不对称裂缝对单井渗流特征的影响.文献[16]在考虑井储系数和表皮系数情况下，建立了一个有限导流不对称裂缝试井分析模型，包括井筒储存和表皮效应，然后利用Laplace 变换和点源积分方法，给出了稳产条件下不对称裂缝井的新解，但并未给出构造点源函数的一般方法.文献[17]讨论了水平井多段压力不对称裂缝的渗流规律.文献[18]讨论了直井压力不对称裂缝的渗流规律，但在不对称裂缝模型的处理方法上采用了文献[16]的结果.文献[19]提出了页岩油气藏水力裂缝有时具有非均质性和随机长度，这给裂缝参数的估计带来了困难，为了更好地评价裂缝参数，将渗流区域划分为三个区（主裂缝渗流区、基质与次级裂缝高渗透的内区、受水力压裂裂缝影响的外区），给出多段压裂水平井非均匀裂缝的试井模型，并考虑了应力敏感，在求解非线性渗流控制方程时，采用了零阶摄动变换进行求解.这为研究复杂裂缝提供了很好的思路与方法.

为了解决不对称裂缝单井渗流模型的Green 函数求解方法，本文借助前人的研究思路[9-11,16]，建立了不对称裂缝的点源数学模型，利用Laplace 变化和点源函数积分方法，给出了如何根据实际问题边界条件来构造恰当Green 函数的方法，使Green 函数简化且容易求解.最后通过与前人研究成果及商业软件计算结果的对比，验证了本文所给方法的可行性.

1 物理模型及基本假设条件

由于复杂的地层条件和水力压裂过程中的不确定因素，导致直井在压裂过程中裂缝关于井筒中心不对称，从而导致渗流方式发生变化，为了更好地建立不对称垂直裂缝试井解释数学模型，参考对称缝的研究思路，以整条裂缝中心为原点建立直角坐标，假设压裂的裂缝延伸方向不变，以裂缝的延伸方向作为x轴，与其垂直的方向作为y轴，井偏离裂缝中心位置的位移为xw（图1）.模型基本假设条件如下：

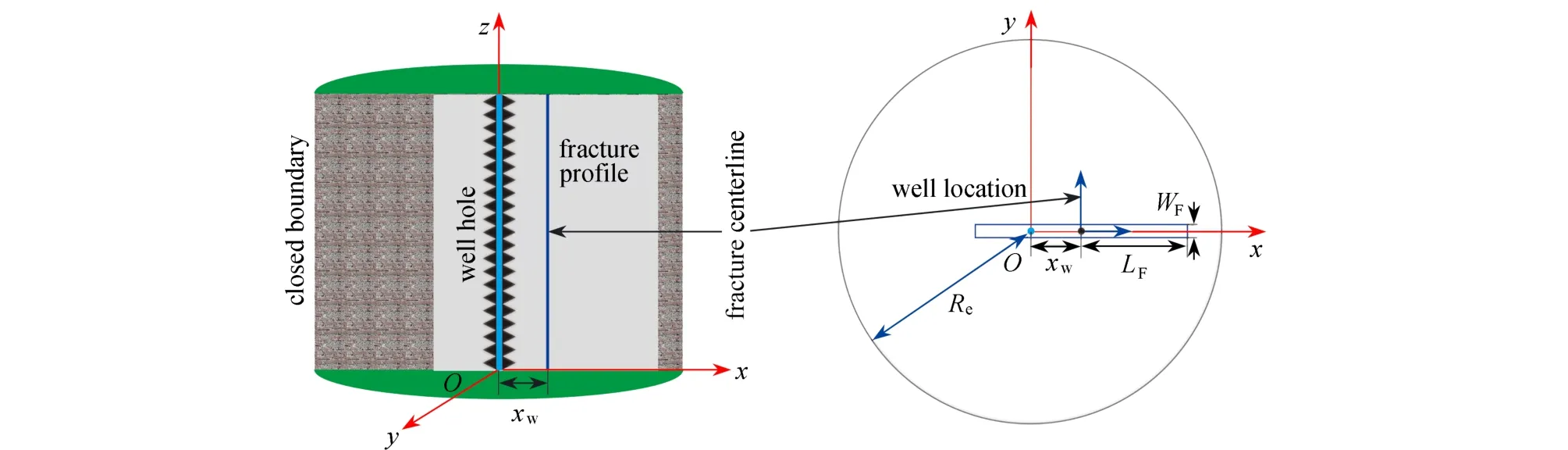
图1 不对称裂缝点源的几何模型Fig.1 The geometric model for the asymmetric fracture point source

① 裂缝两端没有流体通过，裂缝的半长为LF；

② 流体在裂缝和储层中的流动符合Darcy 渗流；

③ 裂缝宽度为WF，裂缝在垂直方向上穿过整个地层；

④ 整条裂缝中压力不相同，即沿着裂缝方向有压降产生，裂缝的渗透率为kF；

⑤ 忽略毛细管压力和重力的影响；

⑥ 储层中的流体为单相微可压缩流体.

2 数学模型及求解

2.1 基本数学模型的建立

对于不对称垂直裂缝，井筒两端裂缝不对称，所以不能将裂缝分为4 部分来计算，而是以裂缝宽度的1/2 为基本单元建立渗流控制微分方程.基于油气渗流的基本原理，根据状态方程、连续性方程和运动方程，建立不对称裂缝渗流微分方程，根据假设条件提出微分方程的内边界条件.根据其物理过程，渗流微分方程可以表示如下：

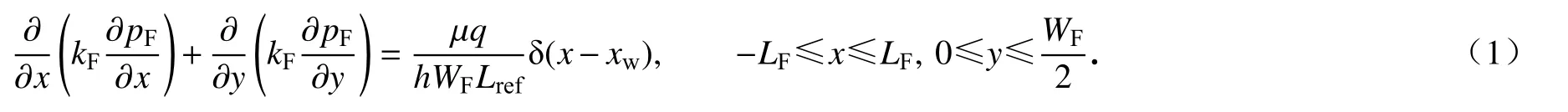
对于水力压开缝而言，其裂缝宽度很小，因此，对裂缝宽度部分进行积分的平均处理可以得到

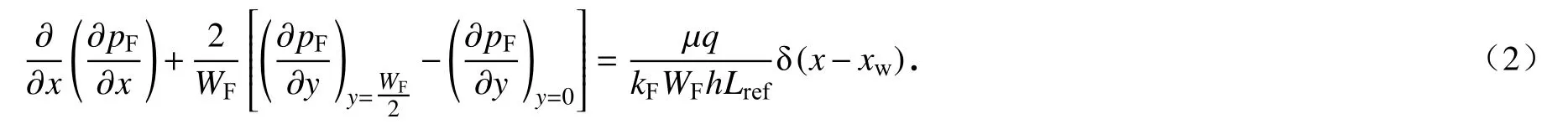
由于裂缝在y轴方向具有对称性，因此，在裂缝中轴线上，流体不流动，可以得到裂缝中轴线上的边界条件为

相对于裂缝长度而言，沿裂缝宽度壁面处流量处处相等，所以有如下关系式：

将式（3）和（4）代入式（2），可得

沿着裂缝x方向单位长度裂缝的线流量为

裂缝两端封闭条件为

对式（5）～（8）进行无因次处理，并对时间进行Laplace 变换可得

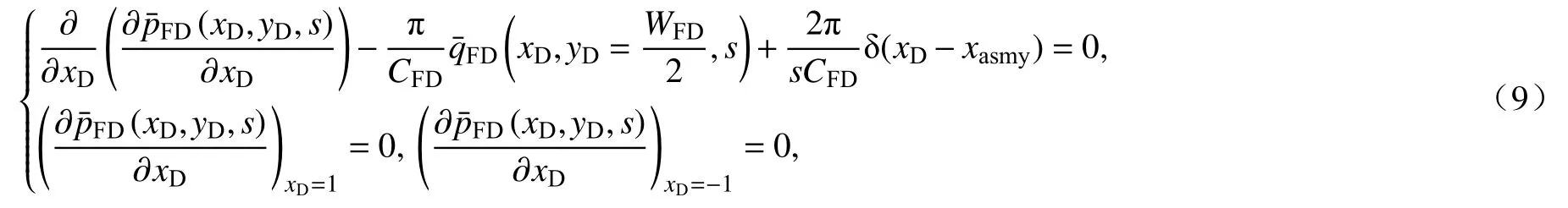
2.2 Green 函数的构造

为了求解式（9），采用Green 函数方法，不妨先假设Green 函数为G(xD;α)，y方向的宽度很小，这里忽略不计，然后根据微分方程的形式和边界条件确定具体Green 函数的表达式.将Green 函数G(xD;α)分别在微分方程（9）左右两边相乘，并沿着x方向裂缝两端的无因次位置从−1 到1 进行积分：

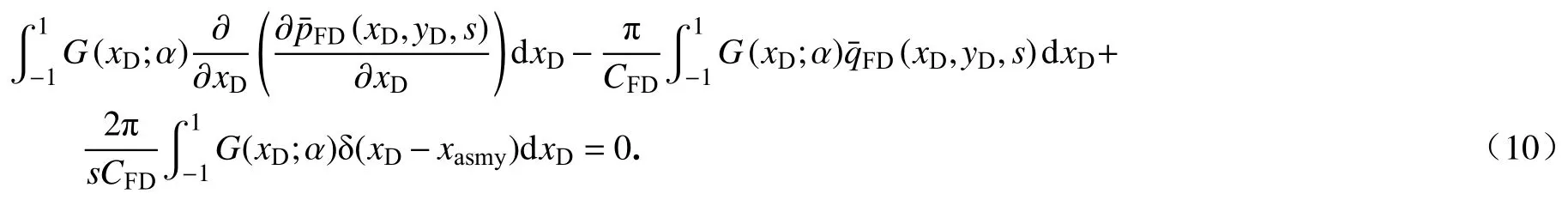
对于式（10）的第一项采用分部积分法，并将式（9）的边界条件代入，再结合δ (xD−xasmy)函数的性质可得

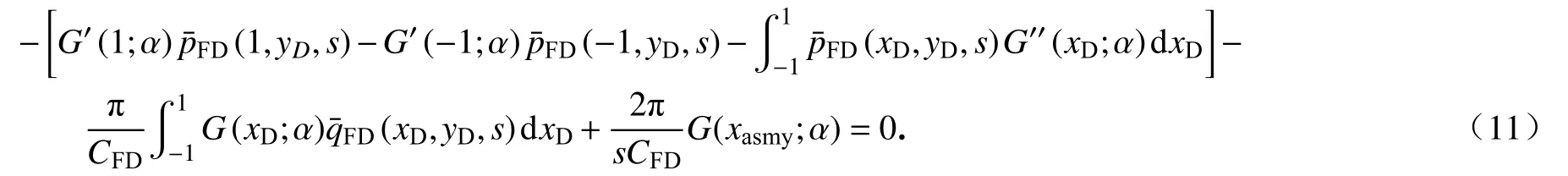
为了求解沿着x方向裂缝的压力(xD,yD,s)，受式（11）中括号的第三项启发，构造的G′′(xD;α)应为一个δ(x)函数的形式，只有G′′(xD;α)为 δ (x)函数的形式，(xD,yD,s)才能脱离积分的形式.因此假设G′′(xD;α)的形式为

其中，F(α)为与原像位置α 有关的函数.为了求解问题的方便，再结合式（11）括号中第一项和第二项的形式，当G′(1;α)=0，G′(−1;α)=0 时，式（11）的第一项和第二项为0，因此得到G′′(xD;α)微分方程的两个边界条件：

对式（13）进行积分，可得

其中

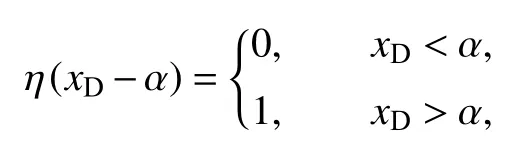
H(α)为与原像位置α 有关的函数.根据式（13）的边界条件可得F(α)=−1/2，G(α)=−1/2，因此式（14）可写成

分析式（13）和（14），G(xD;α)二 阶导函数含有 δ(x)函数，则G(xD;α)一阶导函数应为分段的不连续函数，G(xD;α)应为连续函数.再结合边界条件，则式（15）可写成

对式（16）进行积分，可得

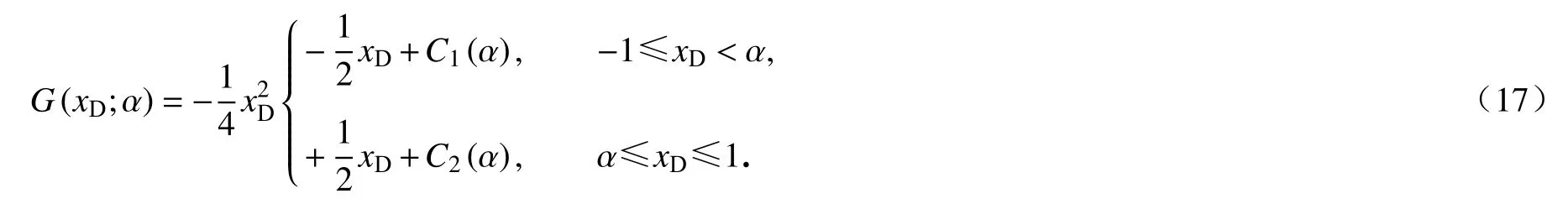
根据G(xD;α)的连续性和对称性，这里的对称性是由裂缝渗流数学模型问题的本身决定的，即位于原像α处的单位源在像xD处生产场的强度与位于原像 −α 处的单位源在像 −xD处生产场的强度相等，即G(xD;α)=G(−xD;−α).

式(2)和式(3)中，b、c、d、e为方程的回归系数，反映自变量对因变量的影响程度，表示当P、A、T1、T2任一自变量变化1%，则会导致 I相应地发生b%、c%、d%、e%的变化。

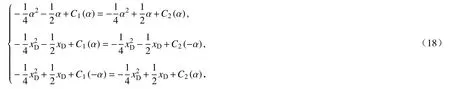
由式（18）可得未知函数C1(α)和C2(α)：

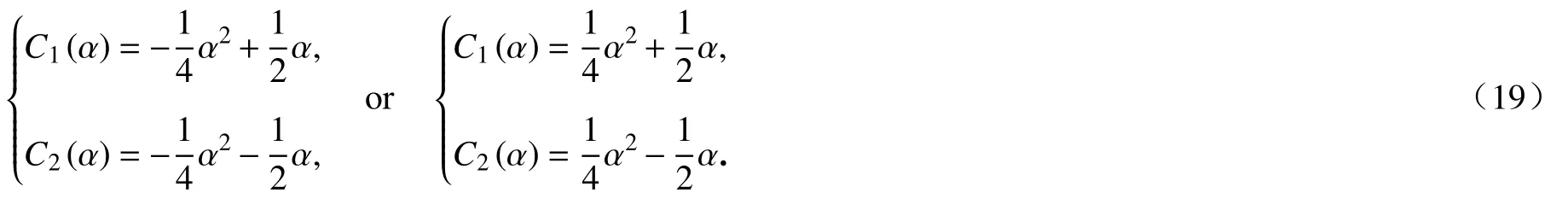
将式（19）代入式（17），可得满足式（9）边界条件的Green 函数：

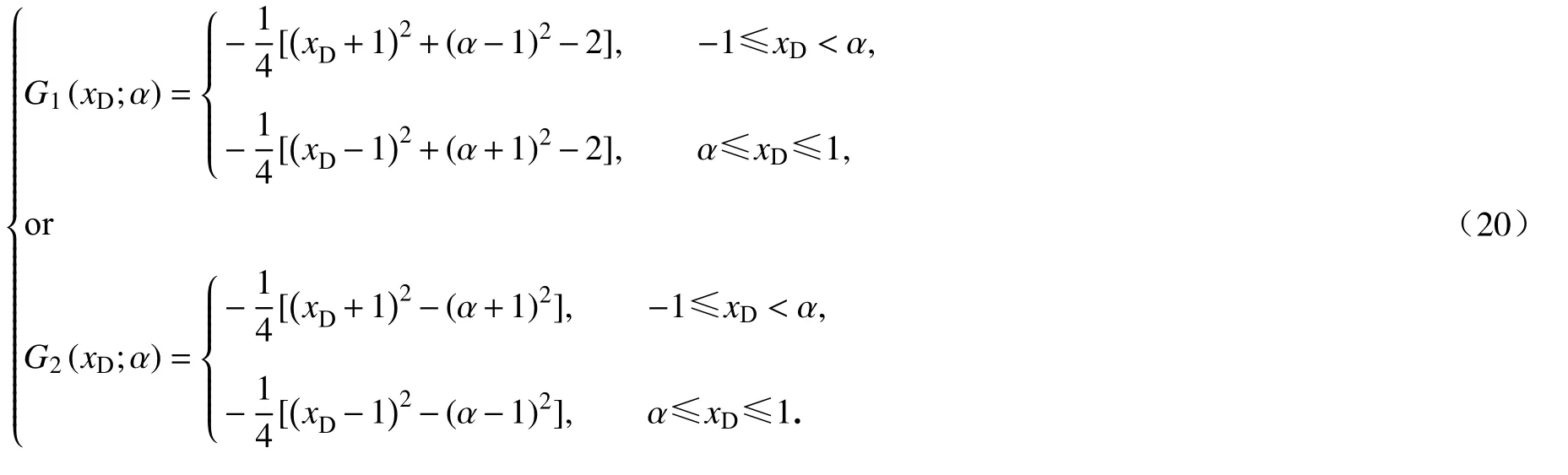
由式（20）可以看出，在使用G(xD;α)的 连续性和对称性求解未知函数C1(α)和C2(α)时，得出了两种不同形式的G(xD;α)的形式，这主要是由Green 函数空间的对称性决定的.将式（13）代入式（11），可解得Laplace 空间沿着x方向不对称裂缝压力的解：

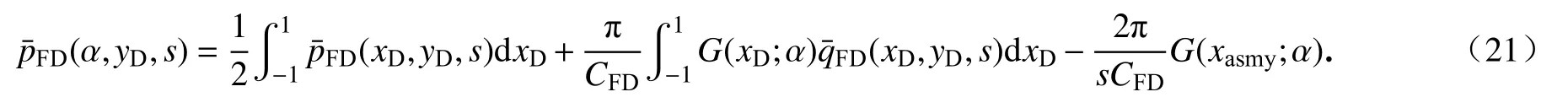
式（21）表示的结果为原像 α位置处的压力.而我们要求解的结果应为像xD位置处的压力，因此可用空间Green 函数的倒易性，即可调换像位置和原像位置.则式（20）、（21）可写成

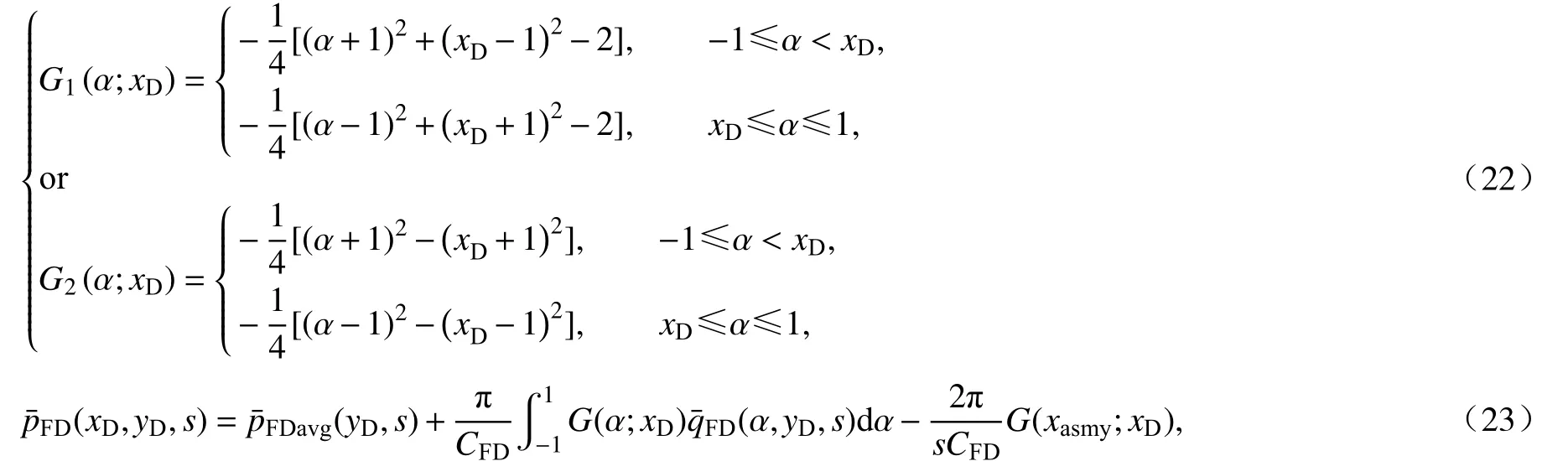
在耦合数学模型求解方面，文献[5-6,11-12,16,20]中做了大量研究.简单的处理方法为：假设式（23）中Laplace 空间裂缝无因次流量在任意裂缝位置处是相等的，即均匀流量法.而复杂处理方法为：假设式（23）中Laplace 空间裂缝无因次流量在任意裂缝位置处是不相等的，即非均匀流量法.本次在压裂直井不对称裂缝模型验证均采用非均匀流量法.网格离散处理方法分为等距离散和文献[18]提出的不等距离散.

3 Green 函数的验证

3.1 不对称裂缝压裂井数学模型

对于不对称裂缝压裂直井而言，假设裂缝沿着x轴方向延伸.我们根据Ozkan 等[21-22]提出的点源函数，得到Laplace 空间的点源解，对点源解进行z方向和x方向的积分，可得到无限垂直导流裂缝的储层模型.在实际研究中，常见的三种不同外边界条件下的储层渗流数学模型可以表示为

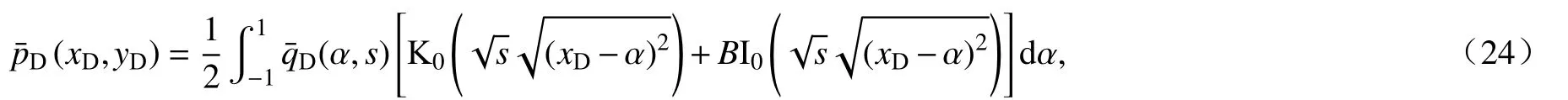
其中，B由边界条件确定.无限大边界B=0，圆形封闭边界圆形定压边界

根据裂缝壁面处压力相等(xD,yD=0,s)=(xD,yD=0)，联立式（23）和（24），可得

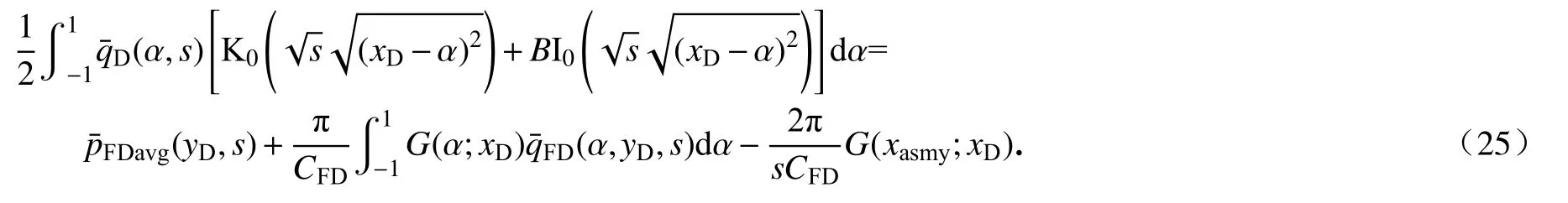
假定在每个裂缝离散单元的流量为常数，对式（25）进行裂缝单元离散，本次研究裂缝的离散方式分为常规的等距离散和文献[18]提出的不等距离散，裂缝的编号都是从左向右依次编号.其离散的方程可表示为

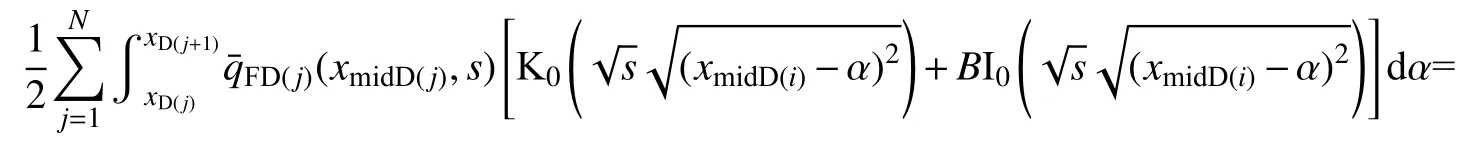
关于式（26）中Bessel 函数 K0(x)的积分问题，笔者借鉴文献[21-22]提出的算法，借助MATLAB 平台，编写了支持向量或矩阵作为传入参数的 K0(x)快速积分函数，具体代码参见本文附录.式（26）中Green 函数积分部分，要根据积分上限和下限与xmidD(i)的 关系，选择恰当的分段函数表达式进行积分.若xmidD(i)的值介于积分下限和上限之间，需要以xmidD(i)为界，将Green 函数积分划分为两段进行.

3.2 不同形式Green 函数计算结果对比

文献[12]给出的Green 函数为式（27），在文献[17-18,20]中，均采用式（27）进行了计算：

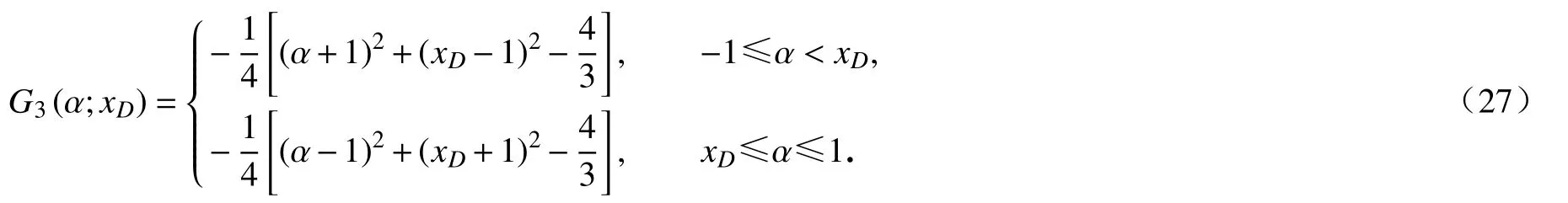
图2为对称裂缝在不同形式Green 函数下的计算结果，其中网格的划分方式采用文献[18]的不等距划分形式，裂缝的总网格数100.裂缝的不对称因子xasmy=0，即对称裂缝.裂缝的无因次导流系数分别取CFD=0.1和CFD=40.模型的边界选择无限大边界，即B=0.通过图2可以看出，本文构造出两种形式的Green 函数在求解对称裂缝问题时，与文献[12]给出的Green 函数计算结果完全相同.图3为不对称裂缝在不同形式Green 函数下的计算结果，裂缝的不对称因子xasmy=0.6，其他参数与图1相同.从图3可以看出，本文给出构造出两种形式的Green 函数在求解不对称裂缝问题时，与文献[12]给出的Green 函数计算结果也完全形同.

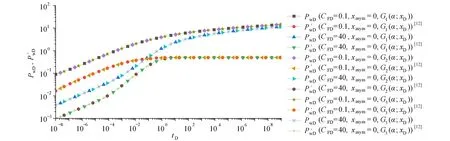
图2 对称裂缝不同形式Green 函数计算结果对比Fig.2 Comparison of calculation results from different forms of Green’s function for the symmetric fracture

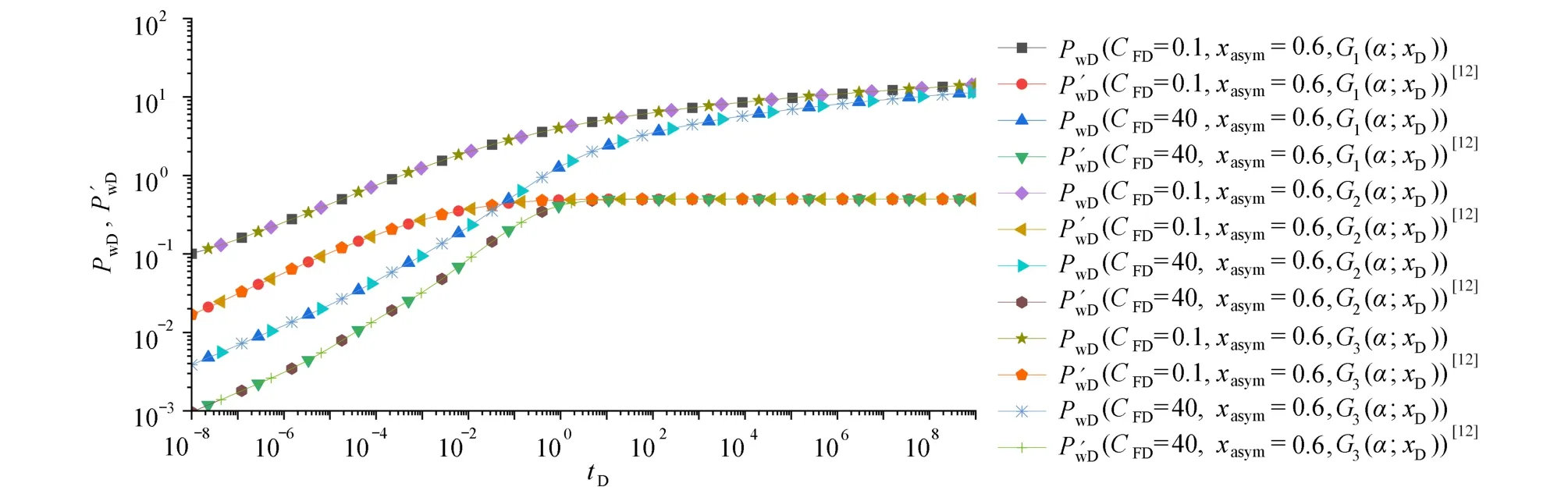
图3 不对称裂缝不同形式Green 函数计算结果对比Fig.3 Comparison of calculation results from different forms of Green’s function for the asymmetric fracture

虽然图2与图3将本文的计算结果与文献[12]做了对比，为了更进一步验证本文的模型可靠性，我们借助油藏动态分析KAPPA WORKSTATION 商业软件的数值试井分析Saphir 模块，建立柱坐标中封闭边界对称裂缝压裂直井的数值模型，如图4所示.实际模型的基本参数如下：储层厚度10 m，储层渗透率18.42 mD，储层外边界半径2 000 m，裂缝半长为100 m，储层的孔隙度10%，储层综合压缩系数为0.000 1 MPa−1，储层温度为100oC，原油的体积系数为1.02，井的产量为100 m3/d，裂缝的导流能力为73 680 mD·m，将其转换为无因次导流能力，即CFD=40.这里需要特别说明的是，当渗透率取18.42 mD，储层厚度取10 m，产量取100 m3/d，则实际的生产压差与无因次压力的数值是相等的，因此可用Saphir 模块数值计算的压力和压力导数值与本文的无因次压力和压力导数计算的数值对比，如图5所示.通过对比可以看出，对于对称裂缝而言，本文给出的Green 函数形式计算的井底压力与压力导数与商业软件KAPPA WORKSTATION 的数值试井分析Saphir 模块数值离散计算的结果一致.

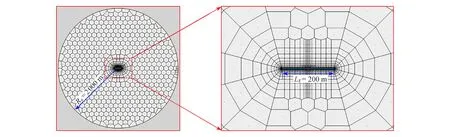
图4 裂缝井的数值物理模型Fig.4 The numerical physical model for the fractured well

图5 解析解与试井分析软件Spahir 数值计算结果对比Fig.5 Comparison between the analytical solution and the numerical calculation results with well test analysis software Saphir

3.3 网格离散方式对计算结果的影响

图6为对称裂缝在不同网格划分方式下计算的结果.裂缝的总网格数100，裂缝的无因次导流系数分别取CFD=0.1和CFD=40.模型的边界选择无限大边界，即B=0.Green 函数选择本文给出的G1(α;xD)形式.通过图6可以看出，对于对称裂缝而言，当裂缝的导流系数越小，等距与不等距网格划分对压力及压力导数曲线影响越大，其主要影响渗流的初始阶段，从曲线的分布情况来看，不等距网格划分更为合理.图7为不对称裂缝在不同网格划分方式下的计算结果，裂缝的不对称因子xasmy=0.6，其他参数与图6相同.从图7可以看出，等距与不等距网格对不对称裂缝与对称裂缝影响的规律一致.由此可以看出，文献[18]给出不等距网格划分方式更加合理，其主要原因是：不等距网格在划分时，沿着裂缝方向，井底附近的网格步长小，离井越远，网格步长越大，这与实际井底压降变化规律基本一致.因此，在研究对称裂缝和不对称裂缝离散数值计算时，若裂缝的导流系数较小，建议采用不等距网格的划分方式.

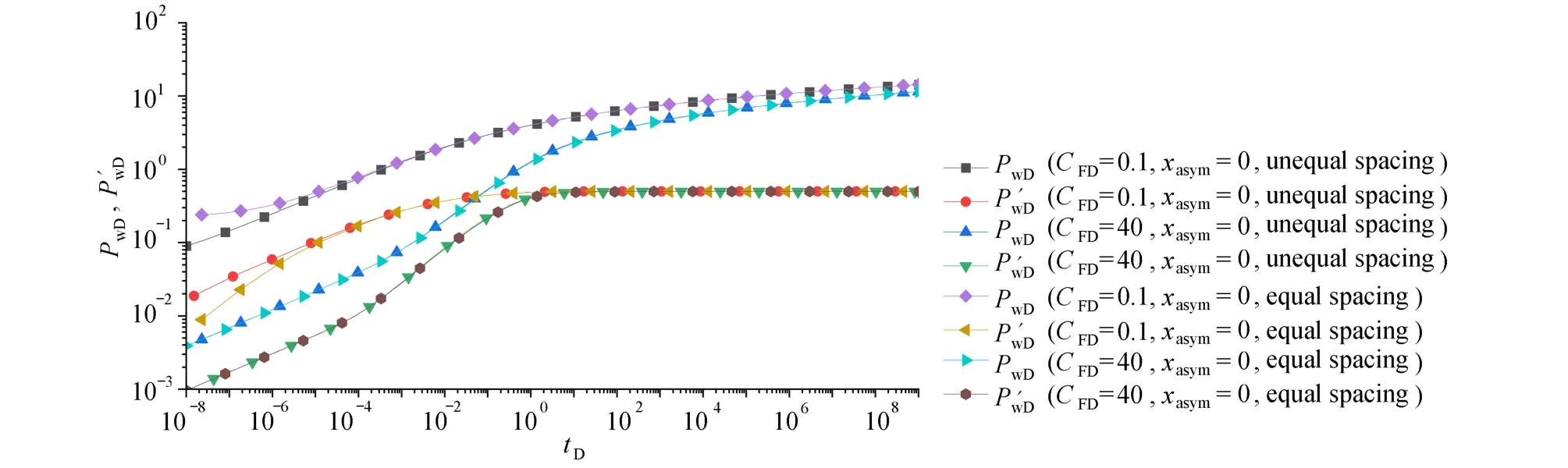
图6 对称裂缝等距网格与不等距网格计算结果对比Fig.6 Comparison of calculation results between the equal-spacing grid and the unequal spacing grid for the symmetric fracture

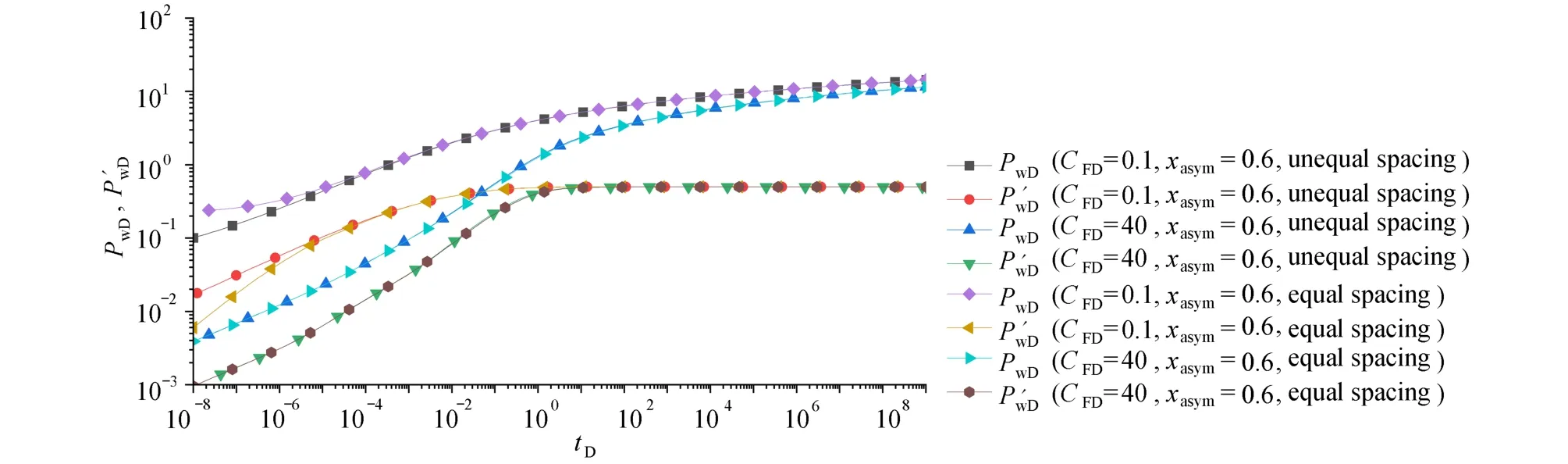
图7 不对称裂缝等距网格与不等距网格计算结果对比Fig.7 Comparison of calculation results between the equal-spacing grid and the unequal spacing grid for the asymmetric fracture

4 结 论

1）本文采用Green 函数方法求解不对称裂缝点源数学模型时，给了Green 函数构造的一般方法，并给出了满足不对称裂缝点源数学模型两种形式的Green 函数，即式（22）.

2）通过不对称裂缝压裂直井渗流数学模型，验证了本文给出的Green 函数两种形式与文献[12]给出的结果在计算对称裂缝和不对称裂缝问题时结果一致.

3）对于对称裂缝和不对称裂缝问题而言，裂缝的导流系数越小，等距与不等距网格划分对压力及压力导数曲线影响越大，主要影响渗流的初始阶段，从曲线的分布形态来看，不等距网格划分更为合理.建议若裂缝的导流系数较小时，采用不等距网格划分.

附录

result=fun_besselk0_int_PAR(x)

erlu=0.577 215 664 901 532 860 606 512 09;

fa=erlu+log(x./2);

fb0=1 − fa;

temp1=0.*x;

temp2=0.*x;

sum1=0;

k=1;

fb1=0.*x;

fc=0.*x;

result=0.*x;

index=x<=20;

while any (any(index))

sum1=sum1+1/k;

fb1(index)= fb1(index)+ (x(index)./2).^(2*k).*(1/(2*k + 1)− fa(index))./(factorial(k)*factorial(k)*(2*k + 1));

fc(index)=fc(index)+(x(index)./2).^(2*k).*sum1./(factorial(k)*factorial(k)*(2*k+1));

if ((max(max(abs(temp1(index)−fb1(index))))< eps)&& (max(max(abs(temp2(index)−fc(index)))

if k>=100 000

warning('计算结果不收敛！ ');

end

break;

end

temp1(index)=fb1(index);

temp2(index)=fc(index);

k=k+1;

end

result(index)=x(index).*fb1(index)+x(index).*fc(index)+x(index).*fb0(index);

result(～index)=pi/2;

index=x==0;

result(index)=0;

index=x<0;

result(index)=0.