基于Monte Carlo算法的复杂机械系统共因失效研究

叶建飞 赵飞豹 张 焱 李 超 王烨君

(西安电子工程研究所 西安 710100)

0 引言

共因失效是一种源于机械载荷、振动、温度、腐蚀等共同因素导致系统内部多个零件发生同时失效的现象。经典可靠度计算方法在计算系统可靠度时作独立不相关假设即假设各个零件之间失效彼此独立，而实际上以载荷为代表的共因失效广泛存在并且会使可靠度计算值出现误差。从20世纪70年代至今,国内外可靠性研究人员对共因失效进行了大量研究，提出包括全概率模型方法、GO法、MCS-CA法、PMS方法等在内的共因失效可靠度建模或仿真方法。其中谢里阳等人针对机械系统共因失效系统可靠度计算问题，在系统层面应用应力-强度干涉理论，结合条件概率方法建立串联、并联系统可靠度全概率计算模型。对于简单串并联系统，该方法性能良好，但是当零件数量较多时存在多重积分计算难度大的问题，此外若系统串并联关系比较复杂甚至无法利用全概率模型方法建模。元胞自动机是Ulam与Von Neumann在20世纪50年代提出的一种用于模拟动态离散系统行为的方法。近年来被广泛应用于如通讯系统、电力传输系统、交通运输系统等复杂二终端二态网络可靠性评估，具备有效判断网络连通性的优势。本文针对全概率模型方法处理复杂机械系统可靠度时的缺陷，从Monte Carlo数值仿真的角度出发，在对全概率模型方法进行分析总结的基础上将复杂机械系统转化为二终端网络，结合元胞自动机思想构建存在共因失效的串联、并联和复杂混联机械系统可靠度算法，并就共因失效对不同类型机械系统可靠度具体影响展开研究。

1 共因失效可靠度全概率模型

机电产品因为成本高昂，失效周期长，难以进行统计学意义上的大量可靠性试验，因此经典系统可靠度方法计算可靠度时通常先利用应力-强度干涉方法计算零件可靠度，然后根据零件间关系建立系统串并混联结构可靠性模型并计算。

对于串联系统

(1)

对于并联系统

(2)

其中代表系统可靠度，和分别代表第个零件广义应力和广义强度，()和()为第个零件广义应力函数和广义强度函数；代表零件数量。

经典系统可靠度模型假设零件之间失效彼此独立，即不存在共因失效，而实际上共因失效在机电系统中广泛存在。谢里阳等人利用条件概率方法，在系统层面应用应力强度干涉理论建立了存在共因失效的系统可靠度全概率模型。以个相同零件构成简单系统并以应力作为主要的失效共因为例。

对于串联系统

(3)

对于并联系统

(4)

其中代表系统可靠度，和S分别代表第个零件广义应力和广义强度，()和(S)为第个零件广义应力函数和广义强度函数；代表零件数量。

对比公式(1)、(3)和公式(2)、(4)可以发现全概率模型在处理应力引起的共因失效问题时区别于经典可靠度方法中对每个零件的应力和强度都进行一次积分的做法，将作为失效共因的应力提取出来只进行一次积分。从Monte Carlo仿真的角度来看系统在任意一次仿真过程中按照经典可靠度的观点各个零件所受的应力彼此不相关，应按照分布独立抽样；而按照全概率模型方法的观点，应力作为失效共因在一次仿真中只应抽样一次。根据实际情况，任意时刻各个零件所受应力与此时输入载荷相关，都可由输入载荷计算或仿真得到，而输入载荷在任意确定时刻为定值，因此全概率模型方法更为贴近实际。

2 全概率模型数值仿真算法

由以上分析本文推断：通过设定引起共因失效的因素在仿真过程中的抽样方式，使其能够反映共因失效的特性将是算法能否准确计算系统共因失效可靠度的关键。

在此基础上构建共因失效全概率模型Monte Carlo数值仿真算法。程序流程图如图1所示。

图1 全概率模型数值仿真算法流程图

1)步骤一：初始化仿真次数=1，系统累计安全次数=0。

2)步骤二：对零件的应力按其分布抽样得；对每个零件的强度按其分布进行单独抽样得,…。

3)步骤三：以成败型零件为研究对象，代表第个零件失效与否的状态，=1表示第个零件安全，=0表示第个零件失效。计算-，若大于0，将置为1，否则置为0，=1,2…。

4)步骤四：给不同类型的系统设置不同的安全条件。判断是否满足安全条件，满足则置系统状态变量=1(表示系统安全),否则=0(表示系统失效)。

5)步骤五：更新仿真次数=+1和系统累计安全次数=+。

6)步骤六：判断仿真次数≤(表示总仿真次数，由人为给定。)若满足则返回第二步，否则终止程序并统计系统累积安全次数，计算可靠度=。

对于Monte Carlo经典可靠度算法只需在此基础上进行少量修改。具体为将步骤二对零件应力独立抽样改为对每个零件分别抽样…。将步骤三中计算-，改为分别计算-若大于0，将置为1，否则置为0，=1,2…，其余步骤不变。

步骤四中安全条件是指系统失效与否的判断依据，对于零部件数量较少，关系简单的系统可以直接给出安全条件的数学公式。

串联系统安全条件为

(5)

并联系统安全条件为

(6)

对于复杂混联系统可以参考Von Neumann型元胞自动机思想，将系统失效与否的条件转化为判断可靠性网络是否导通。以图2所示案例进行说明。

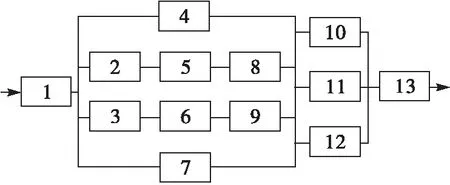
图2 混联模型结构图

编号1-13代表13个零件，按图中连接方式构成混联系统。首先将模型结构图转化为符合元胞自动机思想的可靠性网络，如图3所示。

图3 混联模型可靠性网络示意图

每条边代表一个零件，其对应的状态是1(安全)或0(失效)；每个节点代表一个元胞，其对应的状态是1(激活)或0(未激活)，初始状态是未激活。各元胞状态由箭头指向该元胞的边的状态以及与这些边相连的元胞的状态共同决定，当至少有一条边和与这条边相连的元胞的状态都为1时该元胞的状态为1。以元胞7为例，其状态可以用关联函数表示为

=((2,4),(4,8),(6,9),(2,7))

(7)

式(7)中(,)表示将第个元胞的状态与第条边状态进行“交运算”后的结果，即当第个元胞的状态与第条边状态都为1时，(,)=1。因此当(2,4)，(4,8)，(6,9)，(2,7)中至少有一个为1时，=1。

每次仿真过程中动力由元胞1输入，即首先激活元胞1，经过可靠性网络传输后从元胞9输出。步骤三得到各个零件状态后按照元胞关联函数依次更新元胞状态，若得到元胞9的状态为1，则说明可靠性网络导通，系统安全，否则判定系统失效。

3 算例分析

1)算例1：将上述两个同样的零件串联，分别利用经典可靠性方法，全概率模型方法，Monte Carlo共因失效可靠度算法(以下简称Monte Carlo改进算法)和Monte Carlo经典可靠度算法(以下简称Monte Carlo经典算法)计算系统可靠度，结果如表1所示。

2)算例2：将上述两个同样的零件并联，分别利用经典可靠度方法，全概率模型方法，Monte Carlo改进算法和Monte Carlo经典算法计算系统可靠度，结果如表2所示。

3)算例3：将13个同样的零件按照图2的连接形式混联，分别利用经典可靠度方法，全概率模型方法，Monte Carlo改进算法和Monte Carlo经典算法计算系统可靠度，结果如表3所示。

从表1、表2中可以看出经典可靠度方法计算结果与Monte Carlo经典算法计算结果误差非常小，而全概率模型方法计算结果与Monte Carlo改进方法计算结果也是如此，从而说明Monte Carlo经典算法和Monte Carlo改进算法在计算精度上与经典可靠度方法和全概率模型方法保持一致。

表1 串联系统可靠度计算结果

表2 并联系统可靠度计算结果

对于图2所示的复杂混联系统，在计算过程中发现使用经典可靠度方法和全概率模型方法建模难度较大，而利用Monte Carlo经典算法和Monte Carlo改进算法则较为方便。对比表3中的计算结果，共因失效对该混联系统可靠度的影响表现在使用Monte Carlo经典算法得到的可靠度值小于Monte Carlo改进算法计算结果，可靠度被低估。

表3 混联系统可靠度计算结果

4 共因失效对可靠性影响研究

在Monte Carlo经典算法和Monte Carlo改进算法基础上，将分别就Monte Carlo仿真次数对可靠度计算值的影响、共因失效对串联系统、并联系统和简单混联系统可靠度的影响展开研究。

4.1 Monte Carlo仿真次数对可靠度的影响

以案例分析中定义的零件为基础，将3个相同的零件串联，不断改变仿真次数，利用Monte Carlo经典算法和Monte Carlo改进算法计算系统可靠度，结果如图4所示。

图4 Monte Carlo仿真次数与系统可靠度的关系

随着仿真次数的不断增加，两种方法的可靠度计算值波动程度逐渐降低并趋于稳定。当仿真次数>2000次后，可靠度计算值基本保持不变，为了保证仿真精度在后续研究中可靠度计算仿真次数定为5000次。

4.2 共因失效对串联系统可靠度的影响

以案例分析中定义的零件为基础，将个相同零件串联构建简单串联系统。零件数量由1逐渐递增到10，分别用Monte Carlo经典算法和Monte Carlo改进算法计算系统可靠度，结果如图5所示。从图中可以看出随着零件数量的不断增加，串联系统可靠度逐渐降低。总的来看，由Monte Carlo改进算法得到的可靠度计算值要高于经典可靠度计算方法得到的可靠度计算值，换句话说由于共因失效的存在，利用经典可靠度计算方法计算串联系统可靠度时，可靠度被低估。

图5 串联系统零件数量与可靠度的关系

分析原因在于对串联系统而言，经典可靠性算法将失效共因在不同零件中进行独立抽样，由此统计出的系统失效事件中将某时刻由于共因使多个零件同时失效导致系统发生的一次失效事件多次重复计算，从而导致计算失效率比实际更高，可靠度被低估。

4.3 共因失效对并联系统可靠度的影响

以案例分析中定义的零件为基础，将个相同零件并联构建简单并联系统。零件数量由1个逐渐递增到10个，分别用Monte Carlo经典算法和Monte Carlo改进算法计算并联系统可靠度，结果如图6所示。

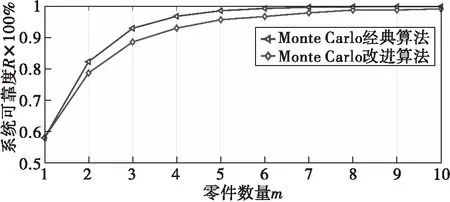
图6 并联系统零件数量与可靠度的关系

从图6中可以看出随着并联零件数量的不断增加，系统可靠度逐渐上升，总体而言由Monte Carlo改进算法得到的可靠度计算值要低于经典可靠度计算方法得到的可靠度计算值，换句话说由于共因失效的存在，利用经典可靠度计算方法计算并联系统可靠度时，可靠度被高估。原因在于对并联系统而言，经典可靠度计算方法将失效共因在不同零件中进行独立抽样，由此统计出的所有零件同时失效事件中，即系统失效事件，忽略了失效共因增加多个零件同时失效概率这个事实，导致系统失效率被低估，可靠度被高估。

4.4 共因失效对混联系统可靠度的影响

以案例分析中定义的零件为基础，通过多个相同零件串并联构建简单混联系统，如图7所示。串联零件数量与并联零件数量之和保持不变，设定+=6。串联零件数量由0个逐渐递增到6个，并联零件数量由6个递减到0个，分别用Monte Carlo经典算法和Monte Carlo改进算法计算混联系统可靠度，结果如图8所示。

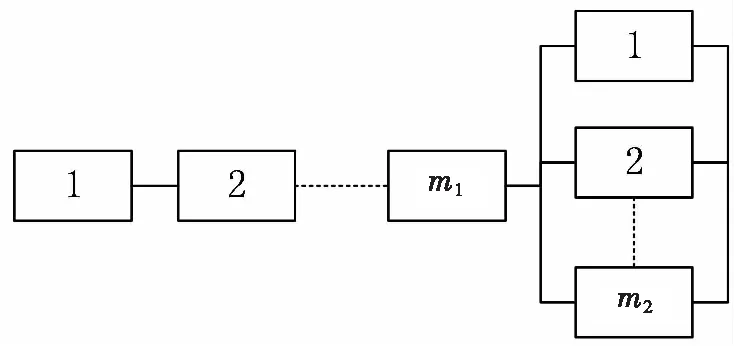
图7 简单混联系统示意图

图8 混联系统零件数量与可靠度的关系

从图8中可以看出，当零件全部为并联时，即=0，=6，利用Monte Carlo经典算法计算的系统可靠度高于利用Monte Carlo改进算法计算的系统可靠度，即可靠度被高估，与4.3中结论一致；而当零件全部为串联时，即=6，=0，可靠度被低估，与4.2中结论一致；当并联零件数量由6个逐渐递减到0个，此时串联零件数量由0个逐渐递增到6个，利用Monte Carlo经典算法得到的混联系统可靠度先高于后又低于Monte Carlo改进算法计算的混联系统可靠度，且存在某个点使两种方法得到的可靠度计算值相等，说明在该点共因失效对系统可靠度的影响被“中和”而不予显现。因此，利用Monte Carlo经典算法计算一个存在共因失效的混联系统可靠度时，鉴于系统结构不同，系统可靠度计算值与实际值相比，可能被高估也可能被低估甚至两者相同，并且总体来看，共因失效对串联系统可靠度影响程度大于对并联系统可靠度的影响程度。

5 结束语

对于存在共因失效的机械系统，利用全概率模型方法可以计算系统可靠度，但是当零件数量较多或者零部件关系复杂难以求解和建模时，利用本文提出的Monte Carlo共因失效可靠度算法可以有效解决这个问题。研究发现当系统存在共因失效时利用经典可靠度计算方法计算串联系统可靠度时，可靠度将被低估；计算并联系统可靠度时，可靠度将被高估；而计算混联系统可靠度时，鉴于系统结构不同，系统可靠度计算值可能被高估、低估甚至与实际值相同，并且总体来看，共因失效对串联系统可靠度影响程度大于对并联系统可靠度的影响程度。